时滞反馈下非线性悬架系统的减振特性研究

王　飞，周继磊，任传波

(山东理工大学交通与车辆工程学院， 山东淄博255049)



时滞反馈下非线性悬架系统的减振特性研究

王飞，周继磊，任传波

(山东理工大学交通与车辆工程学院， 山东淄博255049)

摘要:针对具有时滞减振主动控制技术的非线性悬架，研究时滞和非线性因素对车辆悬架系统减振性能的影响。以一个具有悬架非线性的1/4车辆模型，引入时滞减振主动控制技术，对车身主振动系统进行了减振控制，采用多尺度法推导得出悬架系统振动量与时滞量之间的关系，分析不同振动状态时主系统的振动。利用Routh-Hurwitz判据对悬架系统的稳定性进行判定，得到了系统的稳定性区域。以车身振幅均方根值作为优化目标函数，通过优化设计得到了悬架系统最优时滞反馈系数及时滞量，并在时域下进行仿真分析。仿真结果显示，在简谐激励下和路面随机激励下，有时滞条件下通过调节参数可以使车身加速度均方根值比无时滞时分别降低42.7%和20.9%。研究结果表明通过非线性和时滞反馈联合控制能有效提高悬架系统的减振效果，为悬架系统的仿真分析和优化设计提供了理论依据和设计参考。

关键词:非线性;悬架系统;时滞减振;稳定性

0引言

随着计算机控制技术、控制理论，传感测试技术的日臻完善，主动减振技术在航空航天、工程机械、车辆以及建筑等领域的应用愈加广泛。然而在实际应用中，时滞现象不可避免存在于各种控制系统当中，时滞量虽然很小, 但也将对控制系统的稳定性及控制性能产生一定的影响，因此研究与设计包含时滞因素在内的控制系统将具有深刻的理论意义和实际应用价值[1]。

人们对时滞动力系统进行了大量研究，发现可以通过时滞来对动力系统的振动行为进行控制。N.Olgac等[2-4]最早提出时滞动力吸振器的概念，即在主系统上安装一个基于吸振器质量块位移的时滞反馈控制结构，当外界激励频率与吸振器频率一致时，主系统的振动能被吸振器完全吸收。徐鉴和赵艳影[5-7]研究了时滞对线性、非线性动力吸振器减振效果的影响，证实了可以利用时滞减振技术来抑制系统振动。在非线性动力学研究领域, 时滞可以作为控制和产生系统的复杂运动的控制“开关”，利用时滞进行混沌控制[8-14]。Shin和Kim等[15]利用时滞控制技术对气动隔振板进行了理论研究，并通过试验验证得到较好效果。Nayfeh等[16-17]研究了悬臂梁的多模振动控制，并利用状态时滞反馈对悬臂梁进行控制，起到了很好的控制效果。目前在时滞减振方面的研究大多集中在吸振器、隔振器上，通过有时滞时与无时滞时系统动力学行为进行对比来说明时滞控制对系统减振的作用。吸振器由于本身的工作特性决定其主要工作在共振频率附近，对它的研究也集中在共振频率附近，这显然不能体现出时滞控制对于随机振动系统控制时的优势，同时通过枚举的方法来对系统动力学行为进行研究显然是不全面的。而汽车作为一个复杂的动力学系统，采用非线性悬架进行分析更能反应真实的情况，通过优化设计得到最优的时滞反馈控制参数，能够更全面的反应时滞反馈控制的减振效果；同时汽车的工作环境也十分复杂，在路面随机激励下研究时滞反馈对非线性动力悬架主系统的减振影响是十分必要的。

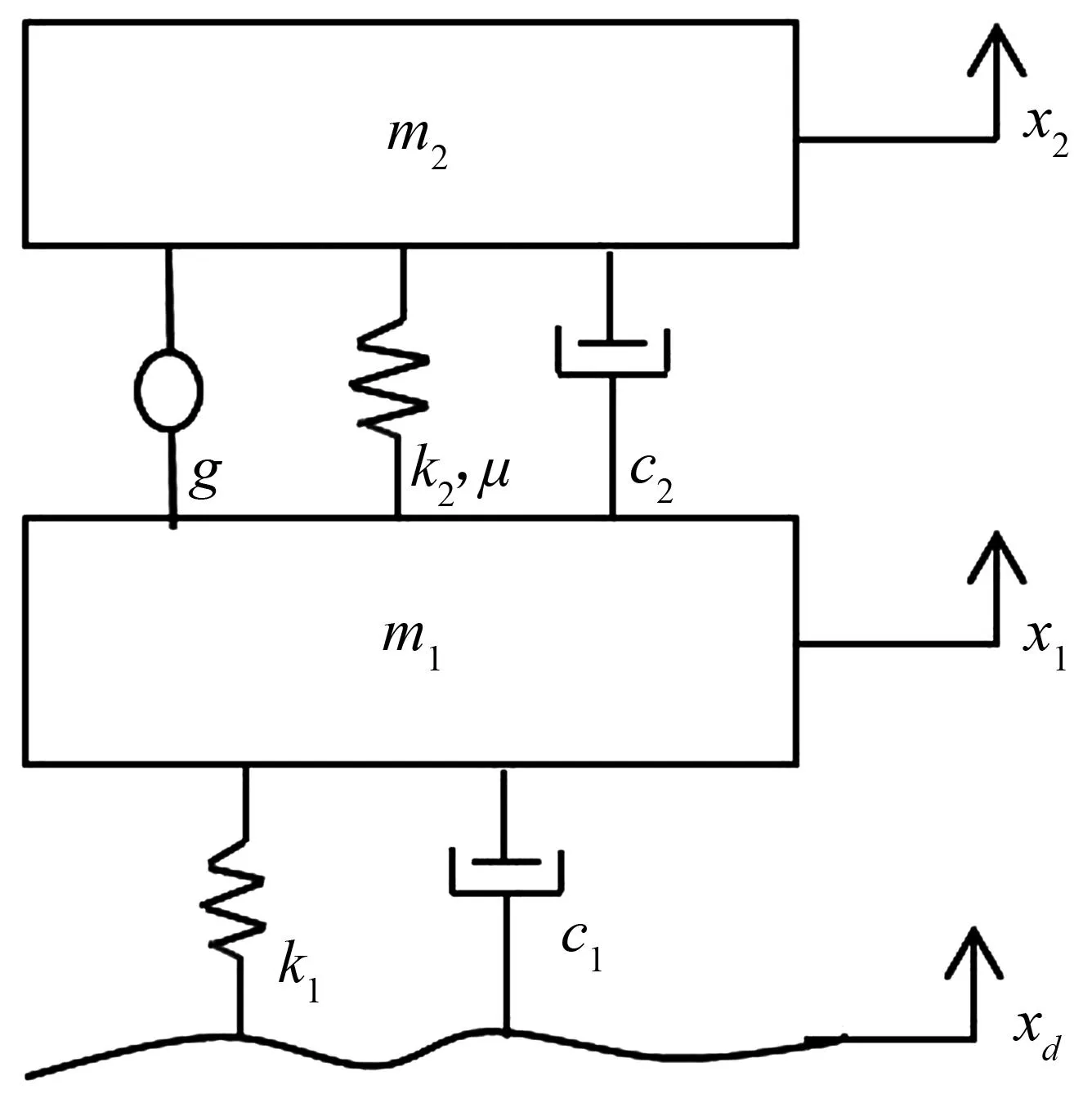
图1　含时滞反馈控制的1/4车辆模型Fig.1　1/4 car model with time delay feedback control

本文针对一个具有悬架非线性的四分之一车辆模型引入时滞减振技术，对主系统(车身主振动系统)进行了减振控制。采用多尺度法研究时滞非线性悬架对振动的响应,分析主系统共振时振幅与时滞量之间的关系，并对系统进行稳定性分析。为了确定减振效果最优的时滞和增益的取值范围，以主系统振幅的均方根作为目标函数进行优化设计，获得悬架系统最优时滞反馈系数及时滞量，并在时域下进行仿真分析。

1力学模型

汽车是一个复杂的振动系统，为便于研究，可以根据所分析的问题进行合理简化。影响汽车行驶平顺性的主要因素是车身垂直振动，因此可以忽略车身的俯仰和侧倾方向上的自由度，仅考虑车身的垂直振动，汽车被分成前后、左右对称的四部分，悬架系统就被简化为1/4车身质量和车轮组成的双自由度系统。图1为一个经过简化的1/4车辆模型，m2为1/4的汽车车身质量，m1为轮胎质量，k1和c1分别为轮胎的刚度和阻尼系数，c2为减震器阻尼系数；悬架弹簧表现为非线性，力与位移之间的关系为f=k2x+μx3，其中k2和μ分别为悬架弹簧的线性参数和非线性参数；假定悬架系统受到周期外激励xd=fcos(ωt)的作用，x1和x2代表轮胎和车身的垂直位移；g(x2τ-x1τ)代表时滞状态反馈，其中g是反馈增益系数,τ为时滞量。

以x1，x2为广义坐标得到悬架系统的运动方程为：

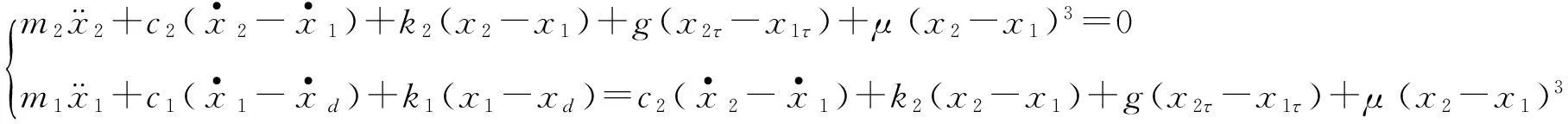
(1)

2系统减振特性分析及仿真

2.1摄动分析

为了简化计算，引入以下无量纲量：

为了便于摄动分析，将其中一些变量重新标度：

ζ1=εξ1，ζ2=εξ2，g=εg*，μ1=εμ*，λ=ελ*，其中0<ε<<1。

(2)

用多尺度法来寻找式(2)的二次近似解，解的形式表示为：

(3)

将式(3)代入无量纲方程(2),并对同一尺度的方程进行分离，得到：

(4)

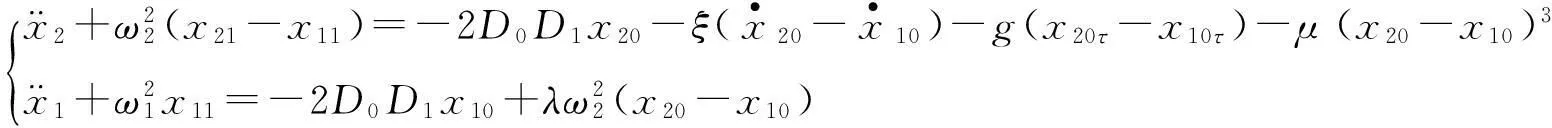
(5)

则式(4)的解为：

如今，除了准备最后一阶段的论文，他还要运营好朱利安葡萄酒学校。让他很开心的是，在这忙碌的一年，他的公司也取得非常好的成绩，其中广州分校的开课量就翻了一番。而对于未来的发展，他希望接下来能尽量减少出差，少点外出参加活动，在他看来，钱是赚不完的，他只想多点留在家里，多一点陪自己的小姑娘，看着她长大。

(6)

当车身质量m2发生共振，即ω=ω2+εσ时，将式(6)代入式(5)，令久期项等于零，并分离实虚变量，得到：

(7)

当轮胎质量m1发生共振，即ω=ω1+εσ时，将式(6)代入式(5)，令久期项等于零，分离实虚变量，得到：

(8)

其中，θ1=σT1-φ1。

当悬架系统不发生共振时，可以得到运动方程：

(9)

2.2平衡解及其稳定性

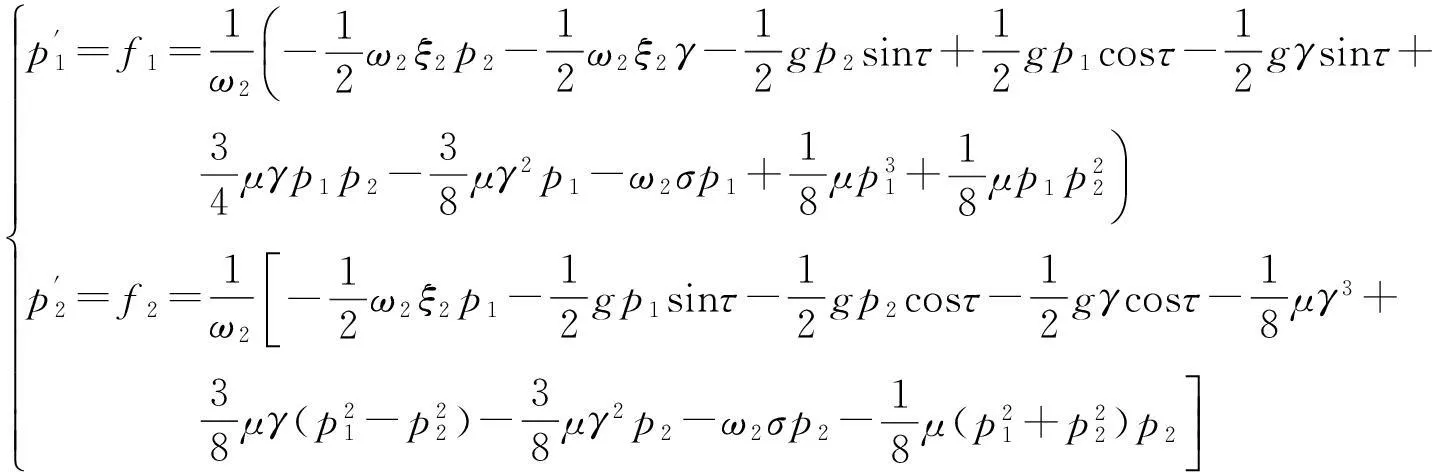
(10)

为了分析平衡解的稳定性,对方程组(10)进行摄动分析,得到方程组的Jacobian矩阵

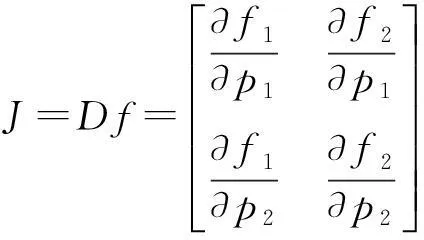
(11)

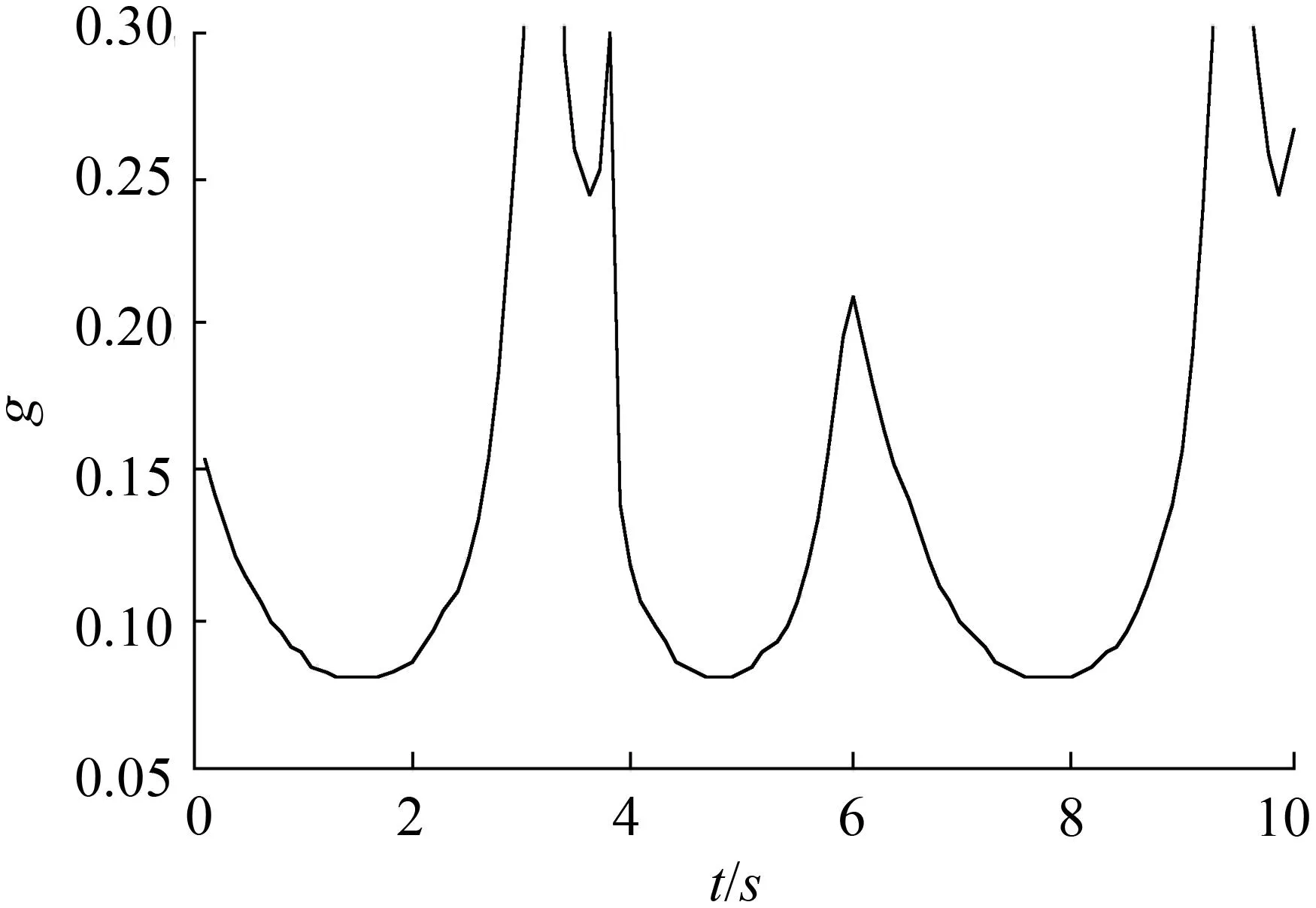
图2　临界稳定状态下g, τ的关系图Fig.2　Relationship between g and τ in the critical stable state

对应平衡点的特征方程可以表示为

aλ2+bλ+c=0。

(12)

应用罗斯-霍尔维兹稳定性判据来判断以上方程的稳定性，可以得到悬架系统稳定的充要条件

a>0，b>0，c>0。

(13)

求出稳定时的g，τ的取值范围，如图2所示，其曲线下方为稳定性区域。由图2可知，当g=0时，不论τ取何值，悬架系统始终是稳定的，但随着g的增大，在τ的一些取值范围渐渐出现了不稳定状态。

2.3时滞反馈对非线性动力悬架主系统的减振影响

为了便于对时滞反馈对主系统的减振影响进行分析,首先研究当外激励频率等于车身固有振动频率时，时滞反馈对主系统减振的作用，取ω2=1,εξ1=0.1,εξ2=0.1,εσ=0.1,εμ=0.1,ελ=0.1，通过数值仿真可以得到悬架主系统振幅随时滞量变化的关系,如图3～图7所示。图3分别为反馈增益系数εg=0.05，0.075，0.08，0.10时主系统的振幅—时滞响应曲线。从图3(a)可以看出,当增益系数εg=0.05时，随着时滞量的增大,主系统的振幅也逐步增大,并当时滞量等于2附近时主系统振幅达到一个极大值。这时如再进一步增加时滞量,主系统的振幅又开始减小,并在时滞等于5附近时达到极小值，之后又逐渐增大，但始终保持在稳定区域之内。随着增益系数的增大，主系统的振幅有一定提高，但仍始终保持稳定，如图3(b)所示。但当增益系数εg=0.08时[图3(c)所示]，在时滞为2、5和8附近，振幅增加明显，而在其他区域，振幅仍然较小，这说明悬架系统的平衡解在这些区域发生了分岔，进入不稳定状态。随着εg继续增大到0.10时，悬架系统的平衡解的不稳定区域继续增大，仅在较小区域内处于稳定状态，如图3(d)所示。

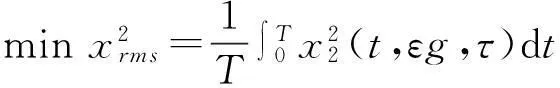
(14)

为了与传统悬架减振效果进行对比,同时为了验证上述理论预测的正确性,现取3组数值εg=0,τ=0，εg=0.1,τ=2和εg=0.069,τ=4.9，并在Matlab/Simulink环境下进行数值仿真，结果如图4和表1所示，其中纵坐标为车身加速度。通过观察可以发现，无时滞的车身振动(短虚线)在稳定后最大振幅维持在1.2。而增益系数和时滞量选取不合适时，车身振动在稳定后振幅相对于无时滞车身振动有了一定幅度的增大，这说明时滞使主系统减振发生了恶化。当增益系数和时滞量取最优值时(长虚线)，主系统振幅有了较大程度的减小，稳定后振幅相对于无时滞条件下减少了42.7%，获得了最优减振效果。这说明合理选择时滞参数对主系统减振可以起到理想的效果。

(a)εg=0.05

(b)εg=0.075

(c)εg=0.08

(d)εg=0.10

(e) εg=0.069

图4　不同时滞时车身加速度的时域仿真图

时滞反馈参数车身加速度均方根值/(m·s-2)对比无时滞时振动变化百分比/%εg=0,τ=00.85780εg=0.1,τ=21.1177+30.3εg=0.069,τ=4.90.4913-42.7

由于时滞减振在减小主系统振动的同时有导致副系统(轮胎)振动能量增大的负作用，因此必须考虑时滞减振对轮胎运动的影响，以防轮胎振幅过大而跳离地面。对轮胎运动的仿真如图5所示，通过对比可以发现，轮胎振动稳态响应幅值增加不超过5%，即轮胎垂直位移相比无时滞控制时基本没有增加，时滞减振对轮胎的不良影响可以忽略。

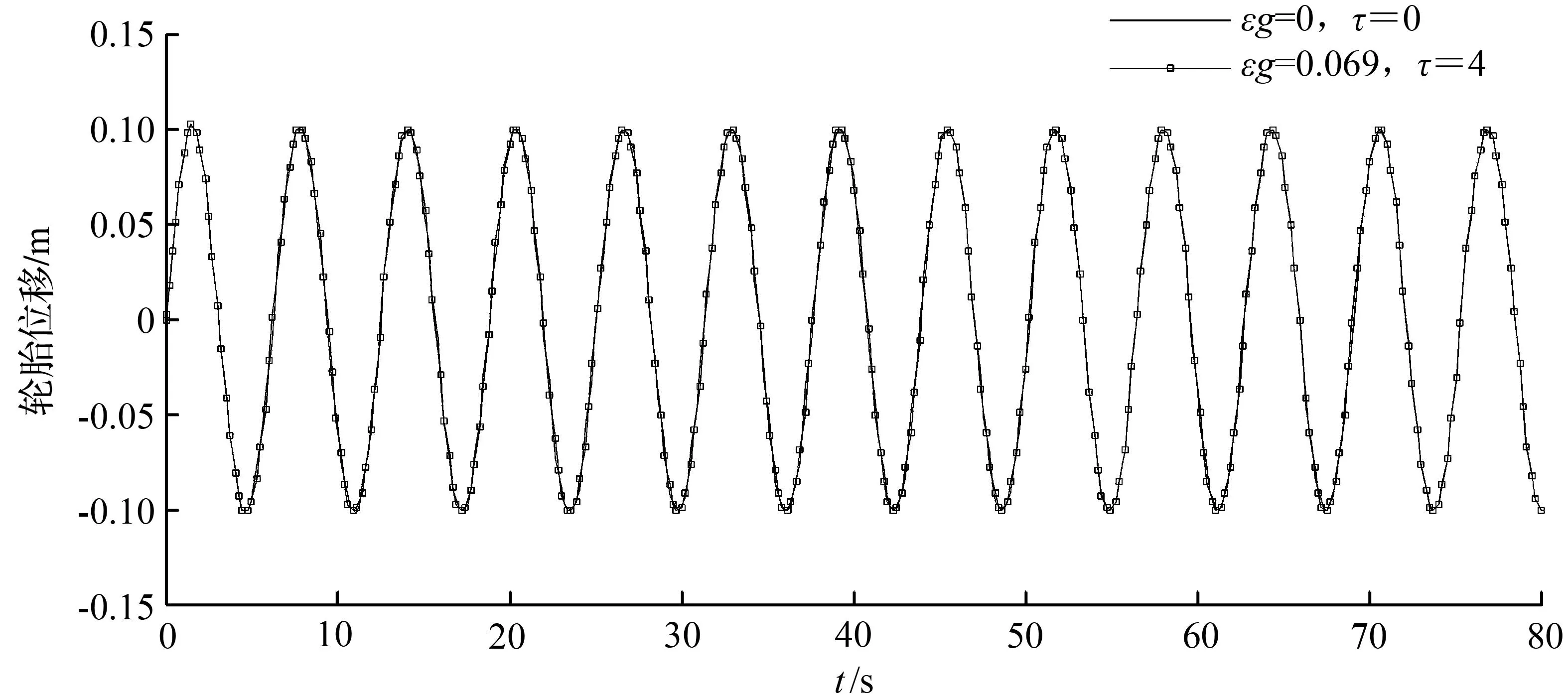
图5　不同时滞时轮胎振动的时域仿真图

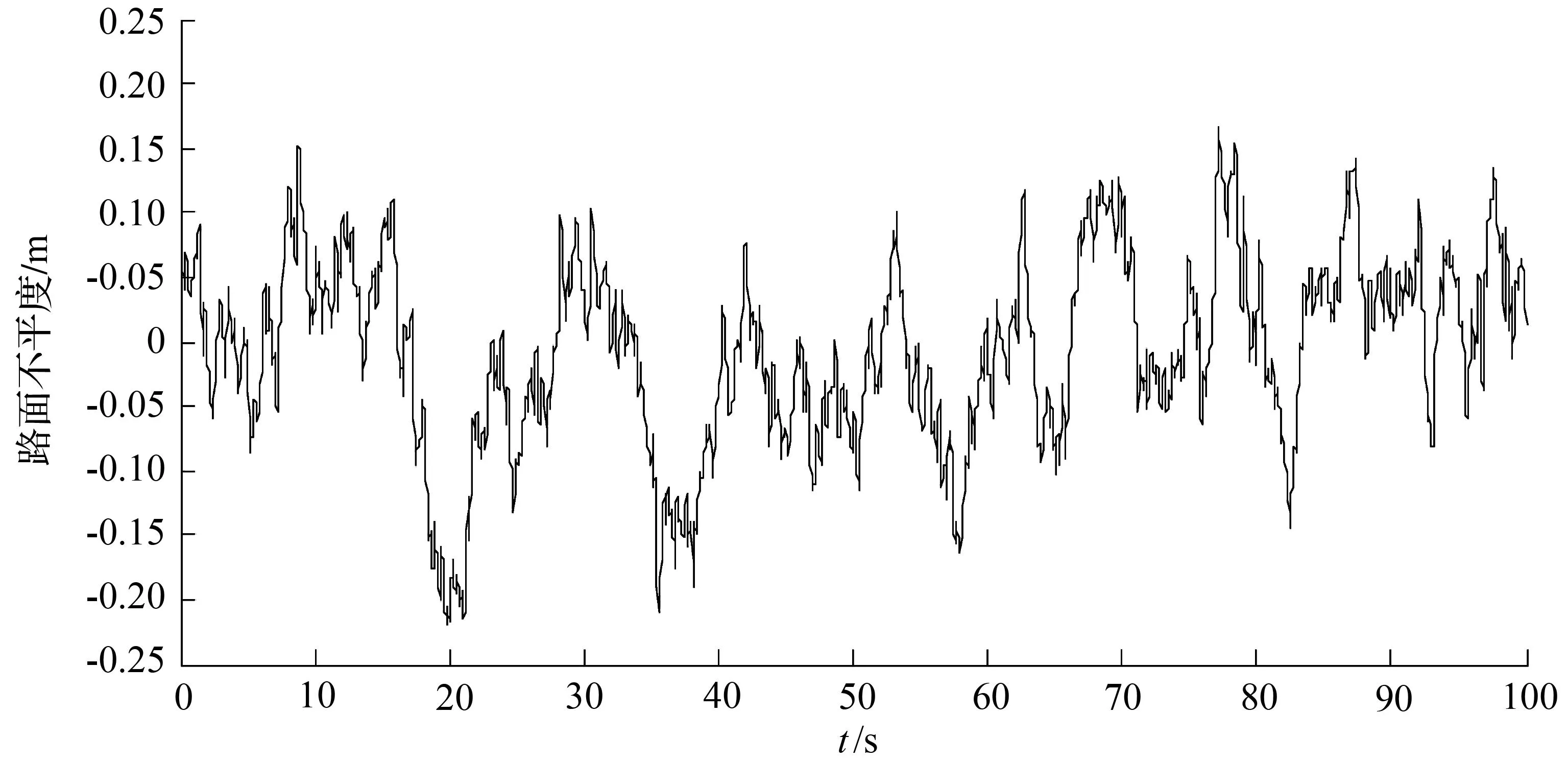
图6　C级路面路谱Fig.6　C level road spectrum

为了进一步验证上述结果的正确性，在路面随机激励下对时滞减振进行进一步的仿真，其中图6为C级路面的时域谱，图7分别是g=0,τ=0，g=1 500,τ=1和g=1 500,τ=1.5时车身振动的时域谱。为方便对比，表2列出了无时滞和时滞控制量分别为g=1 500,τ=1和g=1 500,τ=1.5时车身振动位移的均方根值。通过对比可以发现，g=1 500,τ=1和g=1 500,τ=1.5时车身的振幅相对于无时滞控制时分别有31.1%的增加和20.9%的减小，这说明合理选择时滞参数可以使车身振动明显降低，有效地衰减了车身振动，但是时滞选择的不合理，反而会使车身加速度增加，恶化汽车的行驶平顺性。这表明在随机路面上通过给汽车合理的时滞控制可以使汽车的行驶平顺性得到很好的改善。

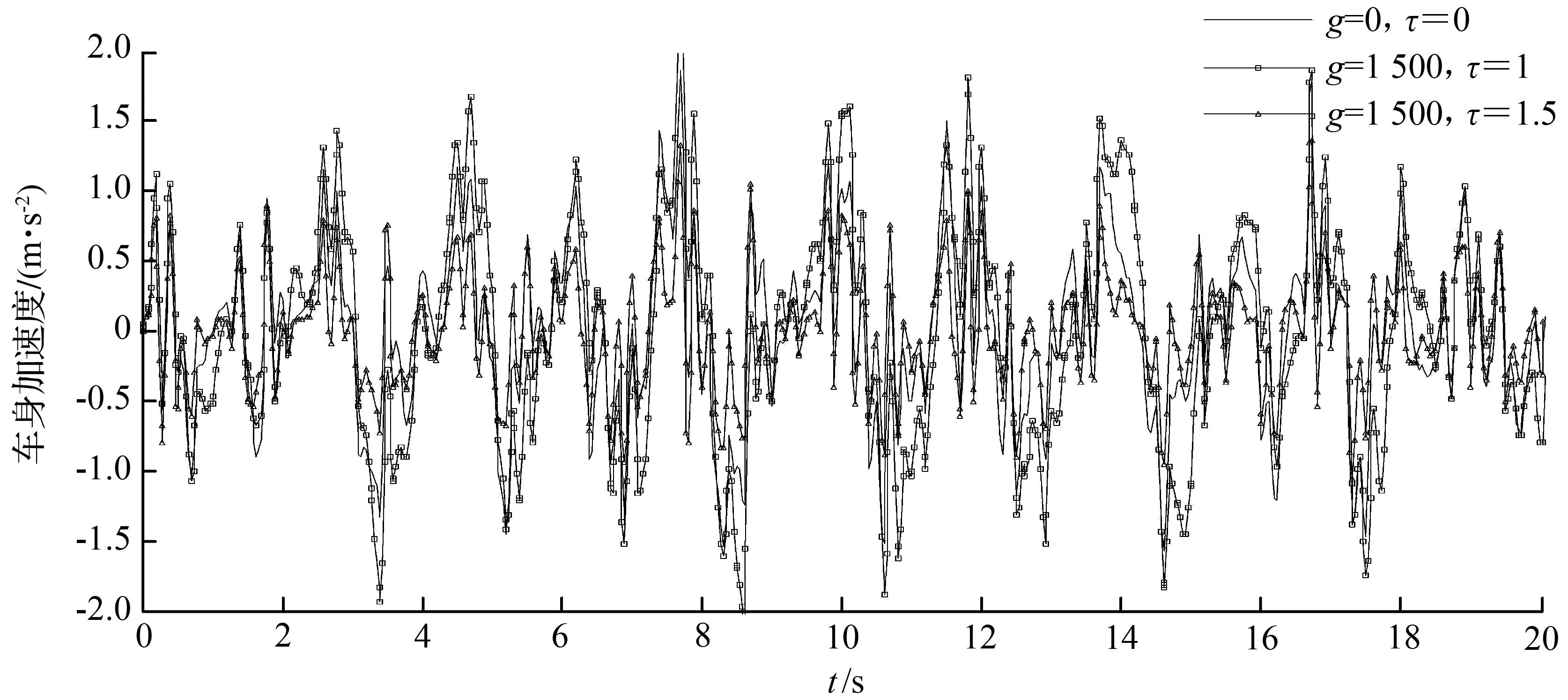
图7　不同时滞时车身加速度的时域仿真图

时滞反馈参数加速度均方根值/(m·s-2)对比无时滞时振动变化百分比/%g=0,τ=00.60210g=1500,τ=10.7894+31.1g=1500,τ=1.50.4759-20.9

3结论

本文在非线性悬架系统中引进一个时滞状态反馈，研究悬架系统在承受外激励时车身质量及轮胎质量的振动情况，分析了非线性和时滞反馈控制的联合作用对悬架系统减振的效果，主要得到以下的一些结论:

①利用多尺度法解出了主系统共振时的运动方程，由此得出主系统共振时与时滞量之间的关系，并进行稳定性分析，得出了悬架系统的稳定性区域。

②对应于不同的时滞反馈系数，得出对应的振幅—时滞响应曲线，并得到最大减振点；同时通过优化设计，得到了悬架系统最优时滞反馈系数及时滞量。

③将得到的优化结果分别在简谐激励和随机激励下验证，结果显示在简谐激励下，有时滞条件下通过调节参数可以使车身加速度均方根值比无时滞时降低42.7%。在路面随机激励下，车身加速度均方根值减小了20.9%。结果表明通过非线性和时滞反馈联合控制能有效提高悬架系统的减振效果。

参考文献:

[1]王在华,胡海岩.时滞动力系统的稳定性与分岔:从理论走向应用[J]. 力学进展, 2013,43(1):3-20.

[2]OLGAC N，ELMALI H，VIJAYAN S.Introduction to the dual frequency fixed delayed resonator[J]. Journal of Sound & Vibration, 1996, 189(3):355-367.

[3]RENZULLI M E, GHOSH-ROY R, OLGAC N.Robust control of the delayed resonator vibration absorber[J]. IEEE Transactions on Control Systems Technology, 1999, 7(6):683-691.

[4]FILIPOVIC D, OLGAC N.Delayed resonator with speed feedback-design and performance analysis[J]. Mechatronics, 2002, 12(2):393-413.

[5]CEPEDA-GOMEZ R, OLGAC N.Exact stability analysis of second-order leaderless and leader-follower consensus protocols with rationally-independent multiple time delays[J]. Systems & Control Letters, 2013, 62(6):482-495.

[6]赵艳影,徐鉴.时滞动力吸振器及其对主系统振动的影响[J]. 振动工程学报,2006, 19(4):548-552.

[7]ZHAO Y Y, XU J.Mechanism analysis of delayed nonlinear vibration absorber[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(1):98-106.

[8]胡海岩,王在华.非线性时滞动力系统的研究进展[J]. 力学进展,1999,29(4): 501-512.

[9]GE Z M, HSIAO C L, CHEN Y S.Nonlinear dynamics and chaos control for a time delay duffing system[J]. International Journal of Nonlinear Sciences & Numerical Simulation, 2005, 6(2):187-200.

[10]XU J, CHUNG K W.Effects of time delayed position feedback on a van derPol-Duffing oscillator[J]. Physica D Nonlinear Phenomena, 2003, 180(1-2):17-39.

[11]徐鉴，陆启韶.非自治时滞反馈控制系统的周期解分岔和混沌[J]. 力学学报，2003,35(4):443-451.

[12]高正晖.一类含连续分布时滞的Lurie控制系统的绝对稳定性[J]. 广西大学学报(自然科学版), 2007, 32(4):350-352.

[13]徐鉴，徐荣改.时滞车辆跟驰模型及其分岔现象[J]. 力学进展，2013,43(1)：29-38.

[14]陈学敏,张国山.时滞非线性系统的模糊保性能控制[J]. 广西大学学报(自然科学版), 2006,36(1):54-58.

[15]SHIN Y H, KIM K J, CHANG P H, et al.Three degrees of freedom active control of pneumatic vibration isolation table by pneumatic and time delay control technique[J]. Journal of Vibration & Acoustics, 2010, 132(5):1741-1757.

[16]ALHAZZA K A, NAYFEH A H, DAQAQ M F.On utilizing delayed feedback for active-multimode vibration control of cantilever beams[J]. Journal of Sound & Vibration, 2009, 319(3-5):735-752.

[17]MASOUD Z N, NAYFEH A H, AL-MOUSA A.Delayed position-feedback controller for the reduction of payload pendulations of rotary cranes[J]. Journal of Vibration & Control, 2003, 9(1-2):257-277.

(责任编辑梁健)

Time-delay vibration damping control of nonlinear suspension system

WANG Fei, ZHOU Ji-lei, REN Chuan-bo

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Abstract:This paper studied the effects of the time-delay and nonlinear factors to suspension damping performance with nonlinear suspension of time-delay active control technology. Time delayed active control technology is applied to 1/4 nonlinear vehicle suspension model to suppress the car-body vibration. The method of multiple scales is employed to deduce the relationship between the vibration of the primary system and the delay, and to analyze the vibration of the primary system in different vibration state. Routh-Hurwitz criterion is utilized to analyze the stability of the system to determine the regions of feedback gain and time delay when it is in equilibrium, and the stability regions of the system is obtained. The RMS (root mean square) of the system vibration amplitude is used as the optimized object function, whose optimal feedback gain and time delay are obtained by optimization technique, and time domain simulation and analysis is presented. Simulation results show that the RMS of vehicle body acceleration is reduced 42.7% on the harmonic road excitation and is reduced 20.9% on stochastic road excitation by adjusting control parameters. The damping effect of suspension system can be effectively improved by using the nonlinear and time-delay feedback control, and this study provides a theoretical basis and reference for simulated analysis and the optimal design of the suspension system.

Key words：nonlinear; suspension system; time-delay damping; stability

中图分类号：U461.1

文献标识码:A

文章编号：1001-7445(2016)02-0379-09

doi:10.13624/j.cnki.issn.1001-7445.2016.0379

通讯作者：任传波(1964—)，山东潍坊人，山东理工大学教授，博士生导师，博士；E-mail：chuanbor@sdut.edu.cn。

基金项目：国家自然科学基金资助项目(51275280)

收稿日期：2015-12-13；

修订日期：2016-01-12

引文格式：王飞，周继磊，任传波.时滞反馈下非线性动力悬架系统的减振特性研究[J].广西大学学报(自然科学版)，2016，41(2)：379-387.