混凝土单轴弹塑性损伤本构模型及参数确定

徐国林,徐　倩，王祥建，齐　虎，柏亚双

(1.西南林业大学土木工程学院， 云南昆明650224;2.中国地震局工程力学研究所， 黑龙江哈尔滨150080;3.中国建筑股份有限公司技术中心， 北京101300)



混凝土单轴弹塑性损伤本构模型及参数确定

徐国林1,徐倩1，王祥建2，齐虎3，柏亚双1

(1.西南林业大学土木工程学院， 云南昆明650224;2.中国地震局工程力学研究所， 黑龙江哈尔滨150080;3.中国建筑股份有限公司技术中心， 北京101300)

摘要：建立一个单轴弹塑性损伤本构模型，给出了理论依据和数值算法，损伤本构模型参数较多，不同参数取值对本构曲线形式影响较大。为了确定合适的本构参数，对单轴本构模型做了参数分析，通过大量的试算，对规范强度混凝土给出了一整套模型参数。计算对比表明：采用建议方法确定本构参数提出单轴损伤本构模型计算混凝土单轴本构曲线与《混凝土结构设计规范》(GB 50010—2010)(简称规范)给出的混凝土单轴本构模型曲线符合较好。文章提出单轴本构模型和参数确定方法，大大简化单轴损伤本构模型在实际工程中的应用，具有一定的理论基础和实用价值。

关键词：混凝土结构；设计规范；单轴本构模型；参数确定

0引言

混凝土材料单轴滞回本构模型，是最基本的本构模型。纤维模型是目前使用最广泛的非线性梁柱模型[1]，而其准确性和数值稳定性在很大程度上取决于其所使用混凝土单轴本构模型的准确性和稳定性。目前混凝土单轴本构模型[2-6]大多采用实验曲线来定义其滞回曲线，但受到实验条件所限很难给出完整的滞回规则，特别是受拉滞回曲线，只有少数学者对其进行了完整的研究，给出了完整的受拉滞回曲线[4]，由于实验条件所限即便是给出滞回曲线其也不完全是客观实验结果，而是参照实验结果按照一定的假设确定。这些包含了主观假定的半实验半经验本构曲线与本构理论存在差异。例如：腾—邹模型[4]受压卸载到受拉时存在刚度突变这显然不合理且在数值模拟中会影响计算的收敛性；过—张模型[5]受压加载后期卸载刚度会变大等。由于基于实验的混凝土单轴本构模型有上述缺点，本文开发基于弹塑性损伤理论的单轴本构模型，该模型能覆盖所有的加载路径(包括实验很难确定的受拉滞回曲线)，且理论完备，模型数值算法不涉及迭代计算，其效率较高，稳定性好。本文模型参数较多，为了方便使用，针对规范混凝土模型，通过大量的试算给出了一套参数便于工程师在实际工程中应用。

1理论基础

1.1弹塑性损伤本构关系

本文模型在有效应力空间计算塑性变形，采用损伤力学模拟材料的刚度退化，并假设材料处于小变形、等温、静载状态下[7-8]。

运用等效应变假设，将材料从有效(非损伤)构型转变为实际(损伤)构型，即非损伤构型的应变与损伤构型相等。

(1)

对式(1)求导可得：

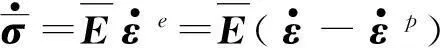
(2)

图1　单轴加载下模型求解示意图Fig.1　The model under uniaxial loading

在实际(损伤)状态下：

(3)

式(3)对时间求导可得：

(4)

式(4)反映了的弹塑性损伤本构关系，由式(4)可知模型的关键是求解塑性应变张量εp和损伤变量d。图1给出了单轴加载下模型的求解示意图。

1.2塑性应变的求解

在有效应力空间求解塑性应变，由于传统塑性力学涉及到的数值算法比较复杂，本文采用经验表达式计算塑性应变，单轴经验塑性应变计算表达式如下：

(5)

式中，βp为控制塑性应变大小的参数。H(·)表示heaviside函数。

有效应力增量可表示为：

(6)

将式(5)代入式(6)得：

(7)

1.3损伤变量的求解

损伤变量可表示为：

(8)

2算法流程

本文模型数值算法如下：

从以上过程可以看出本文模型算法不涉及到迭代，计算效率高，其稳定性好。而目前大多损伤本构模型[9-10]都需迭代计算，不仅计算效率低而且还可能出现不收敛的情况。

3模型参数分析

3.1模型参数对损伤发展曲线的影响

图 2和图3给出了对于函数d=1-1/[1+(aZ)b]其参数a,b对变量d的影响，从图 2和图3可以显示变量d为Z的单调增函数，随着a、b的增加，d的增长速度加快。可见在式(1)中随着a±,b±的增加，损伤变量d±的演化速度加快。

图2b对损伤变量的影响 (a=30)

Fig.2Effect ofb(a=30)

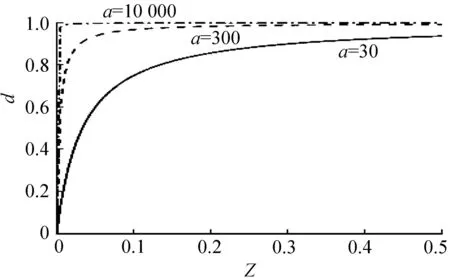
图3a对损伤变量的影响 (b=1)

Fig.3Effect ofa(b=1)

图4给出了a-，b-对混凝土单轴受压应力—应变曲线的影响。从图4可以看出参数a-对模型极限受压承载力影响较大，b-主要影响曲线下降段的斜率。

(a) 受拉骨架曲线

(b) 受拉损伤演化

图4参数a-、b-对模型的影响

Fig.4Effect ofa-，b-on the model behavior

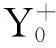
(a) 受拉骨架曲线

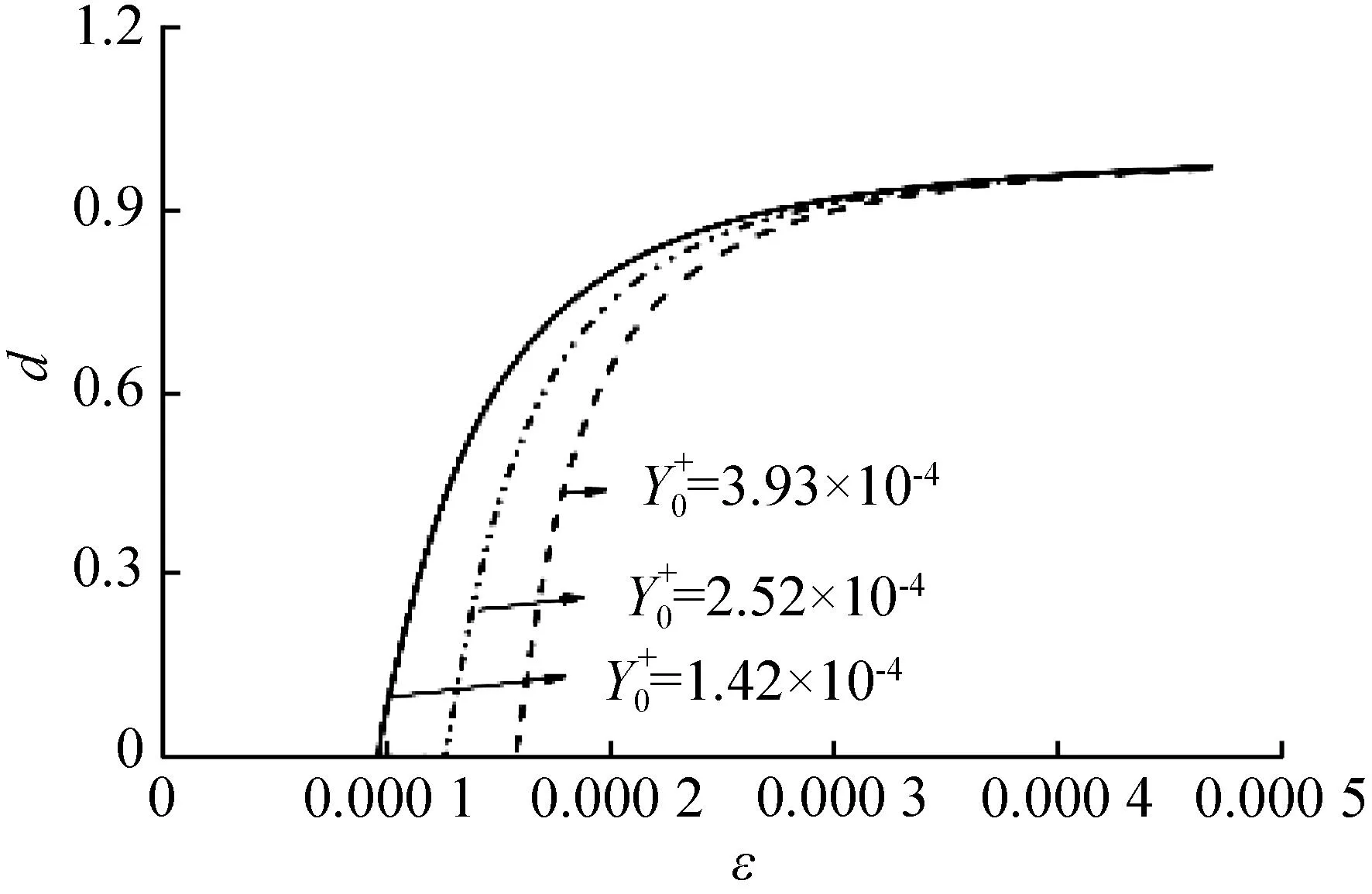
(b) 受拉损伤演化

(a) 受压骨架曲线

(b) 受压损伤演化

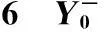
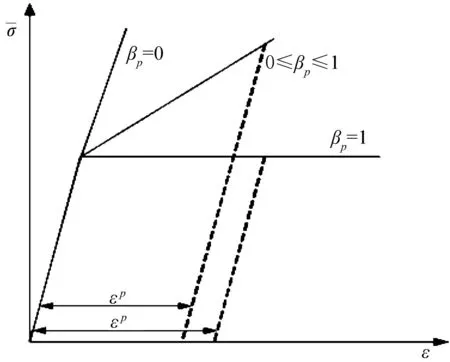
图7　βp对塑性应变的影响Fig.7　Effect of βp

通过将各种参数组合下模型计算结果与实验结果或者规范模型曲线比较，选出与目标曲线符合最好的一套参数即可确定各参数取值。

3.2参数确定

对各种参数组合，模型计算曲线有一定的差别，为了使模型计算结果符合规范混凝土单轴本构曲线，本文将各种参数组合下模型计算结果与规范模型结果进行比较，通过大量试算，得出了一套参数如表1。

表1　各级混凝土材料参数

将本文模型及规范混凝土单轴本构模型在ABAQUS中二次开发[11]，按表1确定本文模型参数取值，本文模型计算结果与规范各强度混凝土单轴本构模型比较如图8所示。

(a) C20(b) C25(c) C30

(d)C35(e) C40(f) C45

(g) C50(h) C55(i) C60

(j) C65(k) C70(l) C75

(m) C80

图9　单轴反复荷载作用下的滞回曲线Fig.9　The model under 1D cyclic test

图9 给出模型在反复拉压加载作用下的全曲线示意图。加载顺序为受拉加卸载(OABO)，受压加卸载(OGCD)，再次受拉加卸载(DEFD)， 再次受压加卸载(DCGH)。

4结语

本文基于损伤理论推导了单轴弹塑性损伤本构模型，并给出了数值算法。在损伤理论中损伤演化的确定需要确定多个参数的取值，因此本文模型参数较多，在工程应用中模型参数的确定需要耗费大量的时间和精力。为了提高模型实用性，本文通过大量试算，对规范各强度混凝土材料给出了一套模型参数取值。计算结果表明：如采用本文单轴损伤本构模型计算混凝土单轴受压骨架曲线与规范给出的混凝土单轴受压骨架曲线符合较好。本文模型数值算法不涉及到迭代与其他损伤模型相比计算效率更高，稳定性更好。

参考文献:

[1]郑山锁,王唯,李龙,等.基于纤维模型的型钢混凝土柱精细化建模分析[J]. 广西大学学报(自然科学版), 2012, 37(2):197-203.

[2]MANDER J B, PRIESTLY M J N, PARK R. Theoretical stress——strain model for confined concrete[J]. Journal of Structural Division, ASCE, 1988, 114(8):1804-1826.

[3]朱伯龙，董振祥.钢筋混凝土非线性分析[M]. 上海：同济大学出版社，1985.

[4]膝智明，邹离湘.反复荷载下钢筋混凝土构件的非线性有限元分析[J]. 土木工程学报，1996，29(2):19-27.

[5]过镇海,张秀琴.混凝土应力—应变全曲线的试验研究[J]. 建筑结构学报, 1982, 3(1):1-12.

[6]齐虎，李云贵，吕西林.箍筋约束混凝土单轴滞回本构实用模型[J]. 工程力学, 2011，28(9):95-102.

[7]齐虎,李云贵,吕西林.基于能量的弹塑性损伤实用本构模型[J]. 工程力学, 2013, 30(5):172-180.

[8]FARIAR O J, CERVERA M.A strain-based plastic viscous-damage model for massive concrete structures[J]. International Journal of Solids and Structures, 1998, 35(14):1533-1558.

[9]VOYIADJIS G Z, TAQIEDDIN Z N.Elastic plastic and damage model for concrete materials: Part I - theoretical formulation[J]. International Journal of Structural Changes In Solids-Mechanics and Applications, 2009, 1(1):31-59.

[10]WU J Y, LI J, FARIA R.An energy release rate-based plastic damage model for concrete[J]. International Journal of Solids and Structures, 2006, 43(3-4): 583-612.

[11]齐虎,李云贵,陈晓明,等.混凝土单轴本构模型研究及ABAQUS二次开发[J]. 建筑结构,2014，44(11):94-96.

(责任编辑唐汉民梁碧芬)

Uniaxial elastic-plastic damage constitutive model and parameters of concrete

XU Guo-lin1, XU Qian1, WANG Xiang-jian2, QI Hu3, BAI Ya-shuang1

(1.Civil Engineering Institute, Southwest Forestry University, Kunming 650224, China;2.Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080, China;3.China State Construction Engineering Corporation Limited Technical Center, Beijing 101300, China)

Abstract:A uniaxial elastic-plastic damage constitutive model of concrete wasestablished, and the theoretical foundation and numerical algorithm weregiven. The model has numerous parameters, the values of which affect the model significantly. In order to determine theproper value of those parameters, parameter analysis wascarried out. Comparison calculation indicates that the uniaxial constitutive curve of the model using the parameters defined from the suggested method fits well with that of the concrete model introduced bythe code for concrete structure design(GB 50010—2010). The proposed uniaxial constitutive model and the determination of parameters can greatly simplify the applicationof the uniaxial damage constitutive model, which has theoretical and practical value.

Key words:concrete structure; design code; uniaxial constitutive model; parameter defining

中图分类号：TU 313

文献标识码：A

文章编号：1001-7445(2016)02-0332-07

doi:10.13624/j.cnki.issn.1001-7445.2016.0332

通讯作者：王祥建( 1977—) ，男，山东莒南人，中国地震局工程力学研究所副研究员，博士;E-mail: wang.xiangjian@ 163.com。

基金项目：国家自然科学基金资助项目( 51208478);云南省科技厅面上项目(2011FZ143)

收稿日期：2016-01-11；

修订日期：2016-03-11

引文格式：徐国林,徐倩，王祥建,等.混凝土单轴弹塑性损伤本构模型及参数确定[J].广西大学学报(自然科学版)，2016，41(2)：332-338.