基于滑面应力场修正的改进极限平衡法

刘 光，陈建生，李明坤

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；

2.河海大学 地球科学与工程学院，江苏 南京 210098)



基于滑面应力场修正的改进极限平衡法

刘 光1，陈建生2，李明坤1

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；

2.河海大学 地球科学与工程学院，江苏 南京 210098)

摘要：结合极限平衡条分法和有限元法的各自优点，提出从有限元法的分析结果中提取出滑动面上的应力分布，然后通过转化求得滑动面上的正应力分布，以此正应力作为边坡滑动面上的初始应力。引入两个未知参数对滑动面上的正应力进行修正，把修正后的滑动面正应力带入极限平衡方程组中，经简单迭代计算，求出未知参数和边坡的安全系数。通过对工程实例的稳定性计算，对比分析该方法和其他常用方法的计算结果，验证了该方法的合理性，其计算结果能够真实反映边坡的稳定状态。

关键词：有限元法；极限平衡法；正应力修正；滑动面；应力分布；边坡；稳定性

滑坡作为全球三大地质灾害之一，一直是国内外学者研究的热点，经过多年来学者们的不懈努力，边坡问题分析方法的研究已获得长足发展。现阶段其计算方法主要是极限平衡法[1]和强度折减法[2]，极限平衡法的广泛应用取得了良好效果[3-4]。但极限平衡法假定各土条为刚体，不能充分考虑土体的应力应变关系，同时其计算结果并不能完全反映边坡的实际稳定状态，因此这些方法存在很多缺陷[5]。为了解决上述问题，国内外学者对极限平衡条分法做了大量的改进工作[6-9]。为了解决极限平衡条分法评价边坡稳定性的局限性，以有限元法为代表的岩土数值分析方法应运而生。这类方法不但能考虑坡体变形对边坡稳定性的影响，而且能通过边坡内应力应变分布分析边坡失稳过程等，但其很难给出具有明确物理意义的稳定安全系数[10-11]。因此，郭子仪等[12]以切向和法向弹簧模拟滑坡体和滑床之间的接触摩擦问题，提出了适合于边坡问题的有限元极限平衡法。于斯滢等[13]、朱大勇等[14]也在有限元极限平衡法方面做出了巨大贡献。但他们的计算过程过于繁琐，不便推广。本文提出了一种新的方法，它通过引入两个未知参数对边坡潜在滑动面的正应力进行修正，然后利用极限平衡条分法，求出两个未知参数和安全系数。无需对条间力进行假设，满足严格的静力平衡条件，并且计算结果比较可靠。

1 安全系数求解

图1为具有一般形状滑动面的二维典型边坡剖面。t(x)、s(x)分别为边坡的上、下部轮廓线，w(x)为边坡土体内水位线，σ0(x)为利用有限元软件计算出的边坡滑动面上的初始正应力，σ0(x)为对初始正应力修正后的滑面正应力，u(x)为滑动面上的水压力，a、b分别为边坡滑动面的左右端点，单位宽度土条重度为w(i)，水平地震惯性力为Kcw(i)，Kc为地震影响系数。

1.1 静力平衡方程

图2为第i条块详细受力分析图，其中单位宽度土条重度w(i)由w1(i)和w2(i)两部分组成，w1(i)为单位宽度土条水位线以上土体的自然重度，w2(i)为单位宽度土条水位线以下土体的饱和重度，i条块底部滑动面的倾角，条间力及滑动面上的正应力和剪应力见图2。

利用有限元软件确定边坡滑动面条上的应力分布，然后将滑体分块，确定任意条块底部中心点的位置坐标(xbi，ybi)，从有限元软件计算得到的应力场中提取出条块底部中心点所在单元的应力信息(σxi，σyi，τxyi)，可得任一滑体底面的正应力：

(1)

式中，βi为条块底部中点切线与竖直方向的夹角，βi=90°-arctan(s′(xbi,ybi))可由几何关系得。

由于σoi是考虑了滑体变形后的正应力，再加上有限元计算中网格划分等因素产生的误差，有限元计算得到的应力场并不能完全反映边坡滑动面上的实际应力状态，需要对其进行适当的修正：

σi=ε(xi)σoi

(2)

(3)

式中：ε(xi)为修正函数，取线性形式；xi为条块底部中心点横坐标(即：xi=xbi)；xa、xb分别为a、b两点的横坐标。

在边坡滑动面上，应用摩尔-库伦强度准则：

τi=(ci+σitanφi)/FS

(4)

式中：FS为安全系数；ci、φi为滑面上土体的粘聚力和内摩擦角。

根据滑体的静力平衡条件，可建立整个边坡滑体的水平，竖向及绕坐标原点力矩的3个平衡方程组：

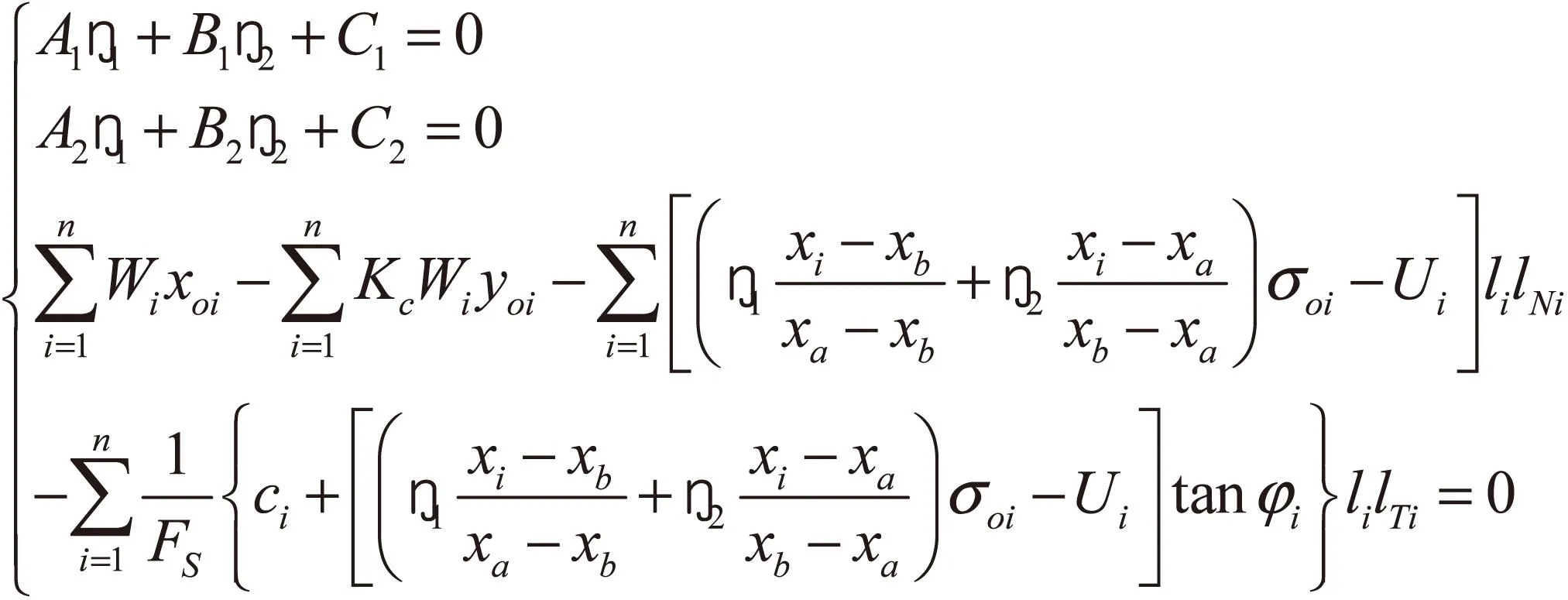
(5)其中：

x0i，y0i分别为条块重心位置的横坐标和纵坐标，lNi，lTi分别为坐标原点到条块底部中点处法线方向和切线方向的距离，可由下式得出：

(6)

(7)

1.2 迭代法求解步骤

总静力平衡方程有三个未知数，分别为：η1，η2和FS，可利用迭代法进行求解，具体求解步骤如下：

(1)初步估算安全系数的取值范围(FS1,FS2)；

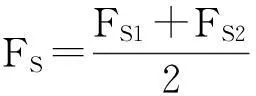
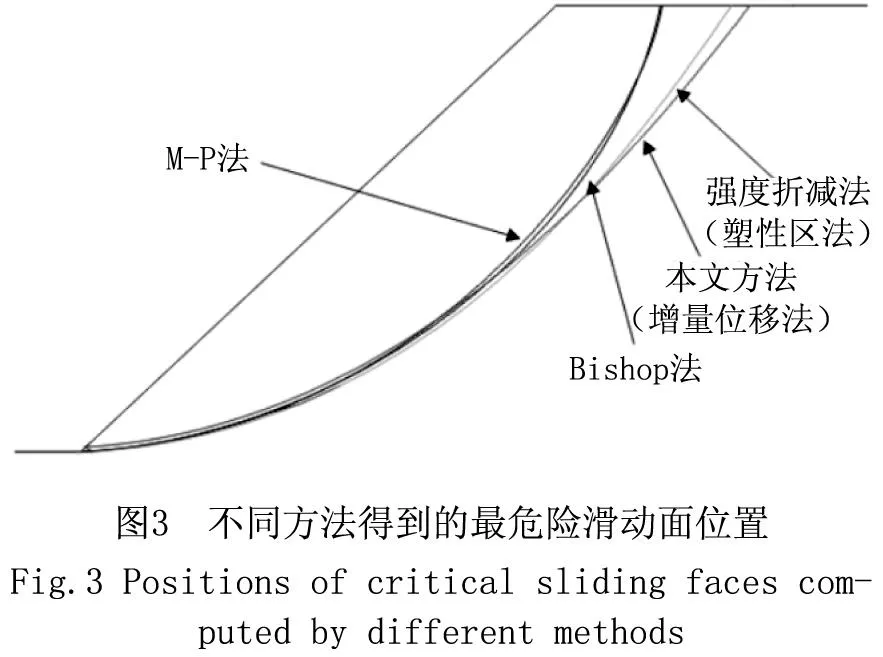
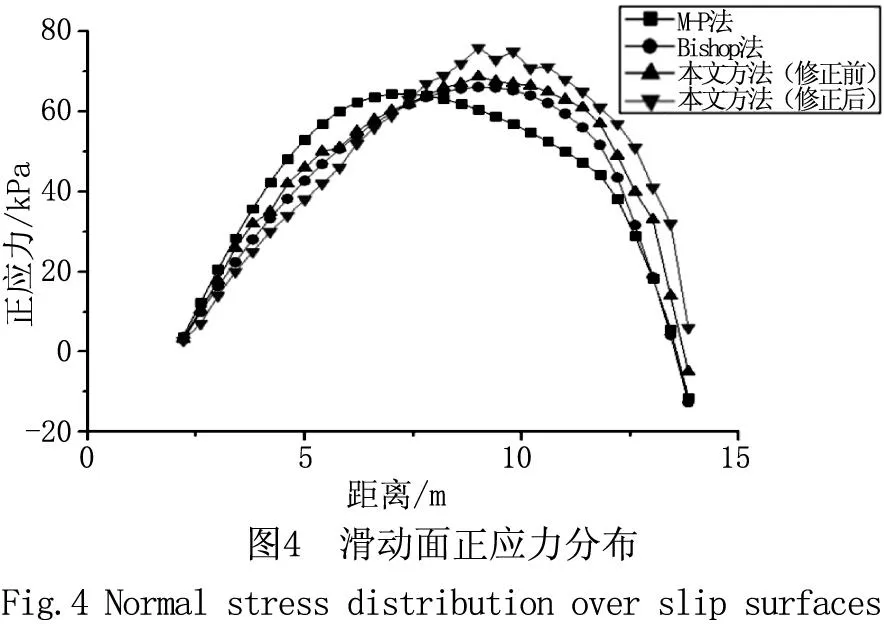
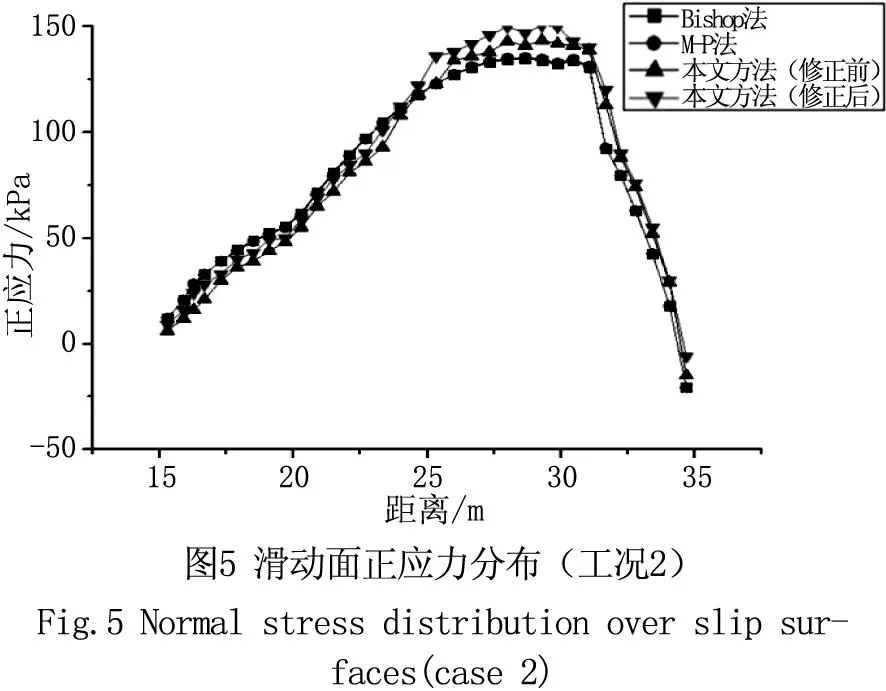
(3)令等式(5)等号的左边等于M，把η1、η2和FS代入等式(5)等号的左边求出M，若-ε

(4)若M>ε，则FS偏大，令FS2=FS；若M<-ε，则FS偏小，令FS1=FS。重复步骤(2)～(4)，直到求得满足精度要求的安全系数的值。

2 算例分析

本文选择Dawson等分析的一个均质土坡作为算例，该边坡为均质土坡，高H=10 m，坡角β=45°，土体容重γ=20kN/m3，黏聚力с=12.38kPa，内摩擦角ф=20°。应用ABAQUS有限元软件计算边坡的应力场，采用增量位移法确定该边坡的临界滑动面，为了便于比较分别采用经典瑞典条分法、简化Bishop法和Morgenstern-Price(M-P)对该边坡进行计算，各种方法得到的滑动面如图3所示。

由图4可知，各种方法所得的滑动面正应力都呈现中间大，两端小的倒U字形，与实际情况相符。在滑动面中下部，有限元法得到的滑动面正应力介于Bishop法和M-P法之间，但是所得正应力值相差不大，这是由于在边坡中下部，这三种方法所求得的滑动面位置基本重叠；在边坡中上部，有限元法所求得的滑动面位置较深，因此所得滑动面正应力值与另两种方法相比较大。由于有限元法充分考虑了土体的应力应变关系，其计算结果更接近真实状态。

表1为各种计算方法所得边坡的最小安全系数，Bishop法和Morgenstern-Price(M-P)法计算的安全系数较大，分别为1.007和1.003；瑞典条

表1 各种计算方法所得边坡最小安全系数

表2 模型材料参数

表3 两种工况下不同分析方法的计算结果

分法不考虑条件力，不满足完全平衡条件，所得安全系数较小，安全系数为0.963；本文方法和强度折减法所得安全系数分别为0.989和0.994，居于中间位置，证明本文所提出的方法是合理的，且计算精度满足要求。

3 工程应用

本文选某断面正常水位和洼地处囤积高水位两种工况。工况1下，路基两边的边坡稳定情况基本相同；工况2下，路基边坡内会形成从右向左的渗流，路基左边边坡更容易发生滑移破坏，因此选取路基左边边坡进行计算完全可以反映整个断面路基边坡的稳定性。路基边坡顶部宽12 m，高8 m，坡度为1:1.5，计算模型从坡角处向外延伸20 m，向下取14 m。模型材料参数见表2。

分别采用极限平衡法、有限元法和本文方法对该断面两种工况下路基边坡进行比较分析。详细计算结果见表3。

由表3可知，本文方法计算的安全系数与有限元法基本相同，处在中间位置，即使在特殊工况下，也能得到满意的结果，再次证明了本文方法计算路基边坡的合理性，能够真实反映边坡的稳定状态。图5为工况2下各种计算方法得到的滑动面正应力分布曲线。从图中可以看出，Biship法和M-P法计算得到的滑动面正应力分布曲线基本重合，本文方法计算得到的滑动面正应力在边坡中下部与前两种方法相比较小，在边坡中上部计算结果相对较大，但4种方法得到的分布曲线相差不大，均在边坡中部达到最大值，而有限元法能够充分考虑土体的应力应变关系，因此最能够反映边坡应力应变的真实情况，本文方法得到的滑动面正应力分布曲线与有限元法能够很好地吻合，这也再次验证了即使在特殊工况下本文方法的计算结果也能够真实的反映路基边坡滑动面的真实应力状态。

4 结论

1)通过公式推导，得出了有限元法和极限平衡法相结合的理论公式，并对公式中未知参数的求解过程给出了程序化编程步骤。

2)结合工程实例，与其他方法计算结果相比，采用本文方法所得边坡的安全系数大小处于中间位置，即使在特殊工况下也能得到满意的结果，验证了本文方法计算边坡稳定性的合理性，其计算结果能够较为真实地反映边坡的实际稳定状态及滑动面应力状态。

参考文献：

[1]ATAEI MS， BODAGHABADI S.Comprehensive analysis of slope stability and determination of stable slopes in the Chador-Malu iron ore mine using numerical and limit equilibrium methods [J].Journal of China University of Mining & Technology, 2008,18(4): 488-493.

[2]王庆乐，周 彬.基于强度折减法对水电站坝头边坡稳定性分析[J].河北工程大学学报: 自然科学版, 2010, 27(1): 34-37.

[3]WEI W B，CHENG Y M，et al.Three-dimensional slope failure analysis by the strength reduction and limit equilibrium methods[J].Computers and Geotechnics，2008，36(1)：70-80.

[4]陈晓磊，孙树林，尚文涛，等.基于坐标输入的电算化边坡稳定性分析[J].河北工程大学学 报：自然科学版, 2013, 30(3): 54-57.

[5]ZHENG HONG，YANG ZHAO LIANG，et al.Extremum solutions to the limit equilibrium method subjected to physical admissibility[J].Natural Hazards，2013，65(1)：79-96.

[6]栾茂田，金崇磐，林 皋.土体稳定分析极限平衡法改进及其应用[J].岩土工程学报，1992，14(Z)，20-29.

[7]ZHU D Y，LEE C F，et al.Generalised framework of limit equilibrium methods for slope stability analysis[J].Geotechnique，2003，53 (4)：377-395.

[8]BENNI THIEBES，RAINER BELL，et al.A WebGIS decision-support system for slope stability based onlimit-equilibrium modeling[J].Engineering Geology，2013，158：109-118.

[9]LOW B K，Gilbert IRB，et al.Slope reliability analysis using generalized method of slices[J].Journal of geotechnical and geoenvironmental engineering，1998，224：350-362.

[10]ZHENG H，LIU D F，et al.On the Assessment of Failure in Slope Stability Analysis by the Finite Element Method[J].Rock Mechanics and Rock Engineering，2008，41(4)：629-639.

[11]RABIE M.Comparison study between traditional and finite element methods for slopes under heavy rainfall[J].HBRC Journal，2014，10(2)：160-168.

[12]郭子仪，范振华，朱云升，等.边坡稳定性分析中的有限元极限平衡法[J].武汉理工大学学报，2014，38(1)：79-84.

[13]于斯滢，邵龙潭，刘士乙.基于有限元极限平衡法的尾矿坝坝体稳定分析[J].岩土力学，2013，34(4)：1185-1190.

[14]朱大勇，李焯芬，姜弘道，等.基于滑面正应力修正的边坡安全系数解答[J].岩石力学与工程学报，2004，23(16)：2788-2791.

(责任编辑李军)

The revised limit equilibrium method on normal stress placed on sliding surface

LIU Guang1,CHEN Jian-sheng2,LI Ming-kun1

(1.College of Civil and Transportation Engineering, Hohai University, Jiangsu Nanjing 210098, China；2.School of Earth Sciences and Engineering，Hohai University, Jiangsu Nanjing 210098, China)

Abstract：Combining the advantages of the limit equilibrium slice method and finite element method, the stress distribution on the sliding surface is concluded from the analysis result of finite element method. Through simple transformation, the normal stress distribution on the sliding surface can be obtained which could be used as initial stress on the sliding surface of slope. Then two unknown parameters were introduced to make correction for the normal stress which will led to the unknown parameter and safety factor of slope by substituting revised normal stress on the sliding surface into limit equilibrium equations and several simple iteration. By comparing the stability calculation results of the method introduced and other normal methods in specific engineering, the feasibility of the introduced method is verified.

Key words：the finite element method; the limit equilibrium method; modifying normal stresses

中图分类号：TU43

文献标识码：A

文章编号：1673-9469(2016)01-0100-05

doi:10.3969/j.issn.1673-9469.2016.01.022

作者简介：刘光(1991-)，男，安徽芜湖人，硕士，研究方向为岩土工程及渗流理论与测试。

基金项目：国家重点基础研究发展计划项目 (2012CB417005)

收稿日期：2015-10-07