“能量穿梭机”实验中的类星体运动

陈耿祥，阮小爽，唐柱荣，黄致新

（华中师范大学物理科学与技术学院，湖北武汉430079）



“能量穿梭机”实验中的类星体运动

陈耿祥，阮小爽，唐柱荣，黄致新

（华中师范大学物理科学与技术学院，湖北武汉430079）

摘 要：通过理论分析建立动力学方程，用四阶Runge－Kutta进行求解，研究了“能量穿梭机”实验仪中的类星体运动.不考虑阻力时，小球会进动并且进动角随圆锥面倾斜角的增大而减小，当倾斜角约为55.6°时，进动消失，小球做类似星体的椭圆运动.考虑阻力时，由于能量损失小球的运动不再有周期性，这与小球在圆锥面上的真实运动相符.

关键词：类星体运动；三维轨迹；四阶Runge－Kutta法

“第12届全国高等院校物理演示实验教学研讨会”论文

指导教师：黄致新（1962－），男，湖北汉川人，华中师范大学物理学院教授，博士，主要研究方向为物理课程与教学论.

物理是一门以实验为基础的科学.物理实验同时也具有重要的教学功能，它不仅可以培养学生的实验观察能力、实验操作能力、分析处理数据能力，还可以培养学生的实验思维能力以及设计实验能力等.特别是物理演示实验教学，一方面可以提供给学生感性的学习材料，加深学生对基本知识的理解认识程度，另一方面也可以激发学生的求知欲，培养学生的科学探索能力［1－2］.

“能量穿梭机”演示实验仪不仅用于演示重力势能、动能、电能等多种形式的能量之间的转化，还用于演示物体的各种运动形式，如斜抛运动、平抛运动、类星体运动.本文对类星体运动进行研究，希望对天体运动有更深的理解.

1 进入圆锥面前的运动

y和z方向分速度大小分别为：

将小球落入圆锥面的时刻记为初始时刻t＝0，如图2所示（设t＝0时刻小球在xoz面）.小球刚刚落入圆锥面而未与圆锥面碰撞时具有沿y和z轴的速度分量v2y和v2z.易得

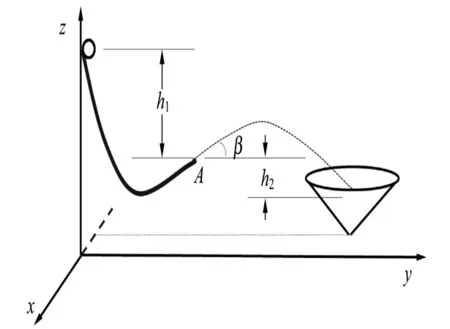
图1 “能量穿梭机”的局部结构简化图

图2 小球刚刚落入圆锥面而未与桶壁碰撞时具有沿y和z轴的速度分量v2y和v2z

当小球落入圆锥面而与桶壁碰撞后具有沿x，y，z轴的速度分量为（0），v2y，（0），如图3所示.其中（0）和（0）分别为：

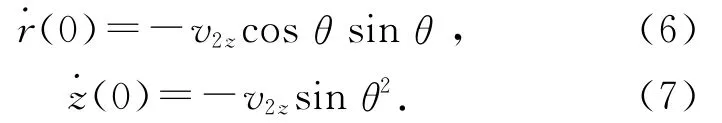
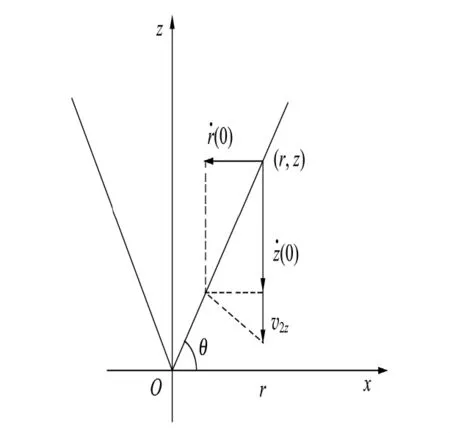
图3 小球刚刚落入圆锥面（t＝0）与桶壁碰撞时具有沿x和z轴的速度分量（0）和（0）

2 理想情况下小球在圆锥面中的运动

2.1 求解小球的运动方程

在理想情况下（即忽略空气阻力和摩擦力）圆锥面上的小球运动较为复杂，存在小球绕z轴的角速度ω（t）.虽然该角速度的大小是随时间变化的，但是由于在z轴方向没有力矩，由角动量守恒可知：如果力矩在某一方向上分量为零，则该方向上有角动量的分量守恒［3］，所以小球对z轴角动量守恒，z轴的角动量大小不变，即

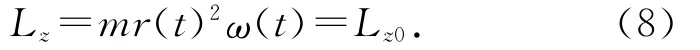
若在静止的笛卡尔坐标系分析角动量将会比较麻烦，所以，本文采用柱坐标系（r，φ，z）并引入瞬时惯性系进行描述（图4）.

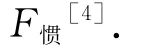
支持力N垂直于圆锥面，重力G方向竖直向下，由于小球存在绕z轴运动的速度，所以有惯性力F惯，方向指向r轴正方向，大小为：

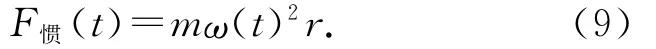
x和z方向上的动力学方程为：

图4 瞬时惯性系，小球在φ＝0平面内时的受力情况

令k＝tanθ，由几何关系知道：

由于z轴方向初始角速度和角动量为：

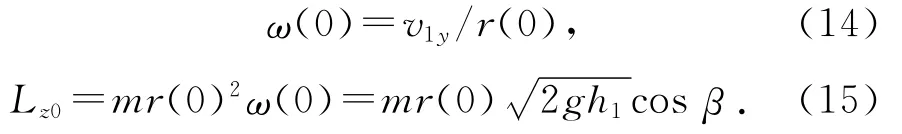
由（8）～（15）式整理可得：

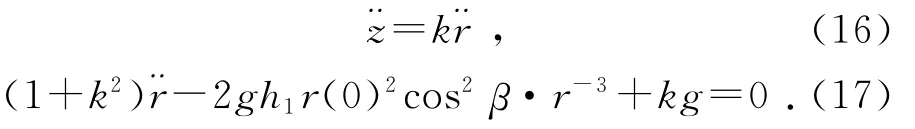
令k1＝2gh1r（0）2cos2β，（17）式改写为：

而（18）式可化为一阶常微分方程组：

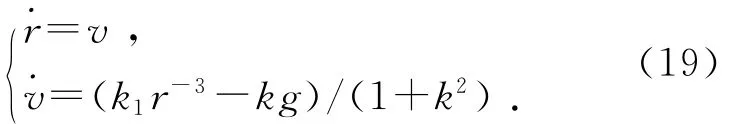
当常微分方程比较复杂时，难以求其解析解，而四阶Runge－Kutta法是一种精度很高的数值求解方法.如下是标准四级四阶Runge－Kutta法［5］：

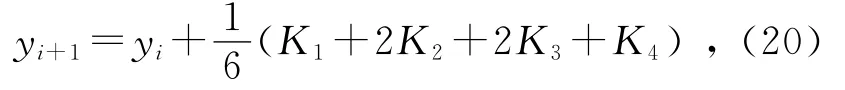
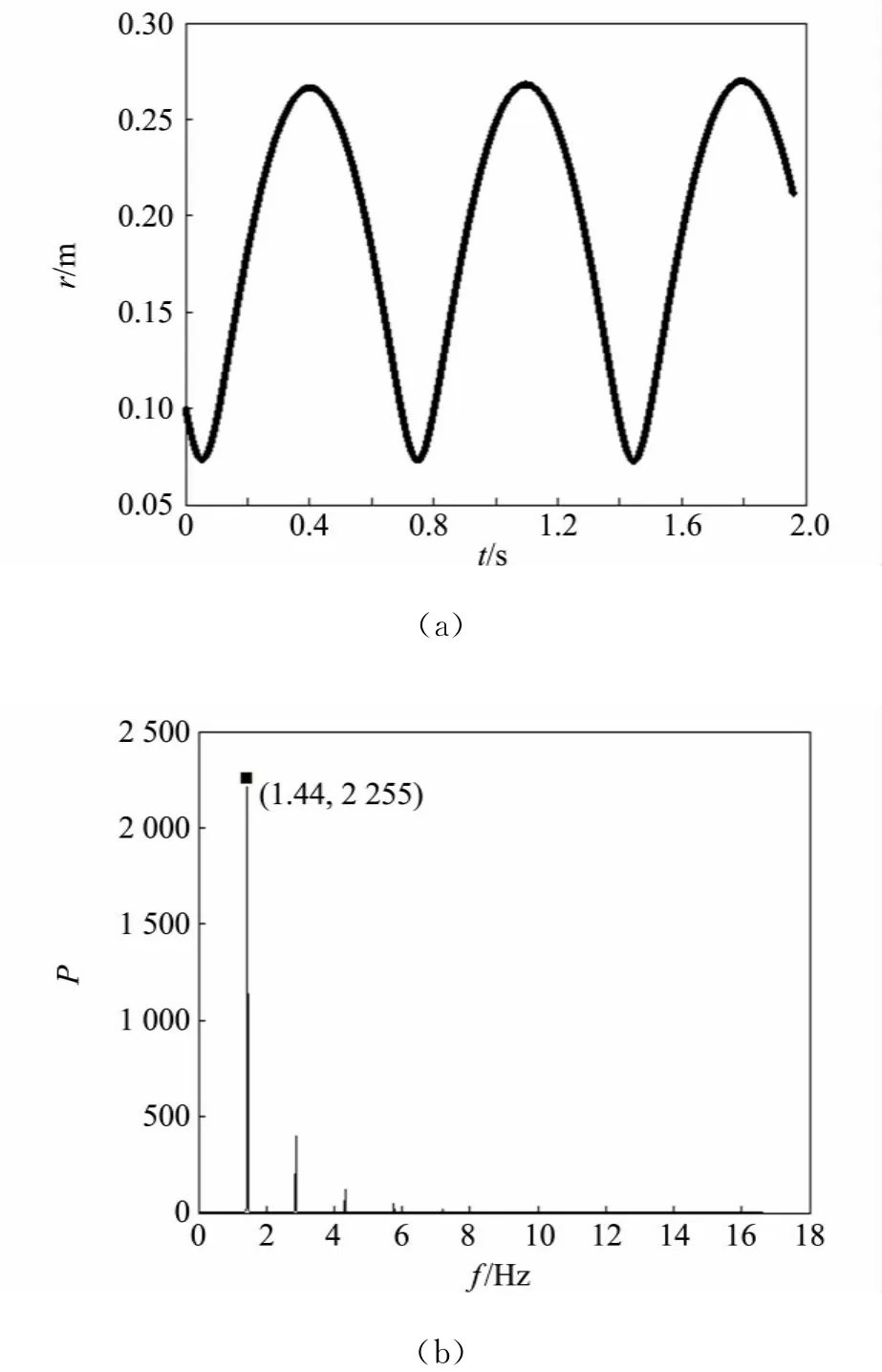
图5 θ＝时r随时间t的变化及其频谱图

2.2 倾斜角对小球椭圆轨迹进动的影响

因为小球同时是绕z轴在旋转，且

只需联立（12），（18），（21）式，便可用Matlab画出小球在柱坐标系中的三维运动轨迹图.图6所示

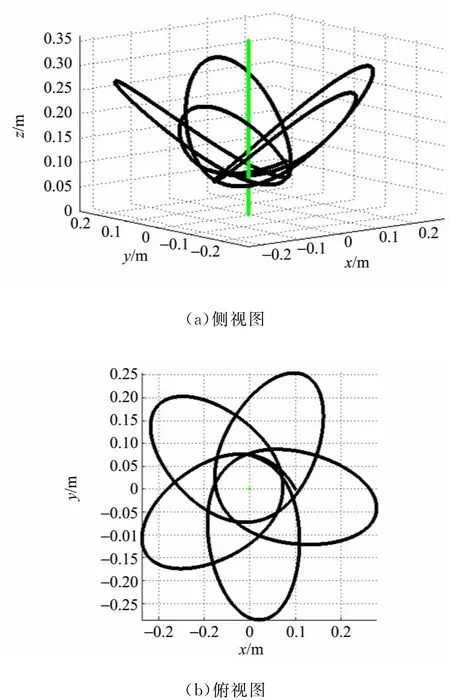
图6 θ＝时类星体三维轨迹图

在55.6°附近存在有趣的现象：进动角是趋于零，即椭圆轨道几乎不变，不发生进动.图8给出了在θ＝55.6°时的类星体三维轨迹（图上画了3个周期的运动轨迹）.倾斜角θ从20°至55.6°对应的ΔΨ＞0，即顺z轴看“椭圆”轨迹存在逆时针进动；而倾斜角θ从55.6°至70°对应的ΔΨ＜0，即顺z轴看“椭圆”轨迹存在顺时针进动，说明这2种情况小球所受合力的方向不在“椭圆”轨道面内，不能形成平面运动.当ΔΨ＝0时小球所受合力在“椭圆”轨道面内，并且容易分析得出此时合力是有心力，故小球的运动形式是平面运动，不发生进动.

图7 不同倾斜角θ对应的“进动角”ΔΨ

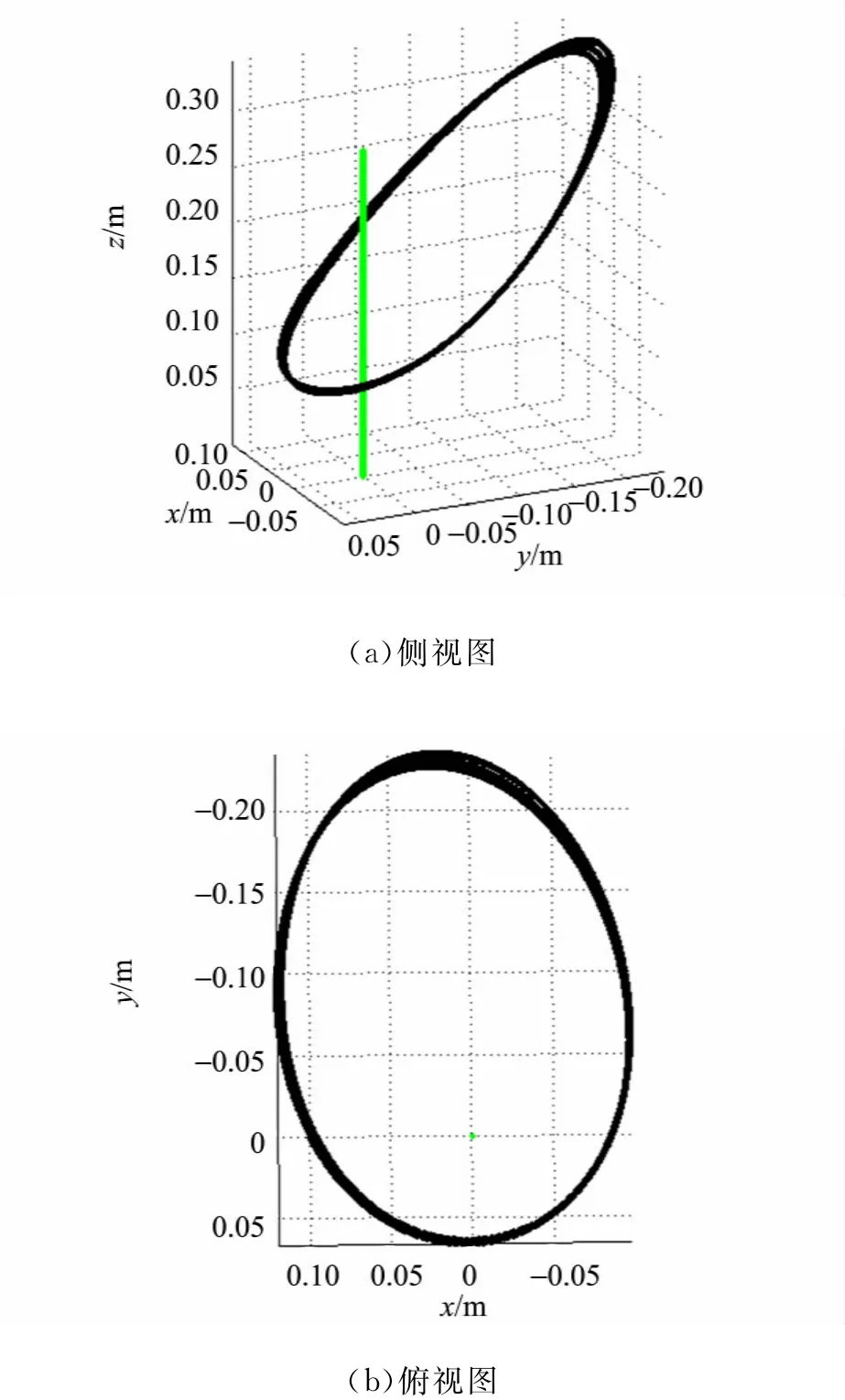
图8 θ＝55.6°时类星体三维轨迹图

倾斜角θ离55.6°越远，｜ΔΨ｜就越大，椭圆轨迹进动越明显，而实际中大部分做椭圆轨道运动的星体，其运动轨迹几乎是确定的，进动很缓慢.所以“能量穿梭机”中圆锥面的倾斜角应在55.6°附近.

3 考虑阻力时小球在圆锥面中的运动

现在考虑由空气和摩擦引起的阻力，假设阻力大小与速度一次方成正比，即f＝－μmv，则（10）和（11）式的动力学方程应改为：

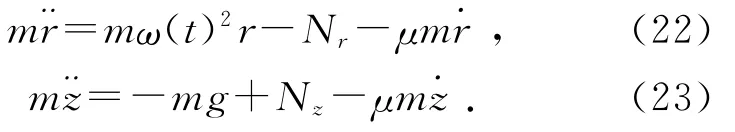
由于受到阻力在z轴方向就会受到力矩，从而角动量的大小会发生改变.用M表示z轴方向阻力力矩的大小

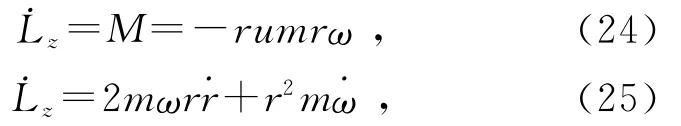
由（24）式与（25）式可得：

由（12），（13），（22），（23）式可以得到与（18）式相似的动力学方程：

联立（26）～（27）式，采用四阶Runge－Kutta法进行求解.

图9 θ＝，β＝，μ＝1.2Ns·kg－1·m－1时r随时间t的变化和类星体运动的三维轨迹图

4 结束语

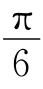
参考文献：

［1］ 帅厚梅，王华.新课标下中学物理实验教学方法的探讨［J］.物理实验，2008，28（4）：18－21.

［2］ 张礼，左玉生，吴弘，等.物理实验教学方法的研究与发展［J］.实验技术与管理，2015，32（10）：197－220.

［3］ 沈惠川，李书民.经典力学［M］.合肥：中国科学技术大学出版社，2006：19.

［4］ 强元棨.经典力学（上册）［M］.北京：科学出版社，2003：120－121.

［5］ 李乃成，梅离泉.数值分析［M］.北京：科学出版社，2011：275－276.

［6］ 奚梅成.数值分析方法［M］.合肥：中国科学技术大学出版社，2003：336－336.

［7］ 祁国良，曲胜艳，谭晓春，等.物理演示实验改进之管见［J］.物理实验，2015，35（7）：19－22.

Study on similar celestial movement in energy－transfer machine

CHEN Geng－xiang，RUAN Xiao－shuang，TANG Zhu－rong，HUANG Zhi－xin
（College of Physical Science and Technology，Central China Normal University，Wuhan 430079，China）

Abstract：Based on Newtonian mechanics，the dynamic equations of the ball were established and the numerical solution was got by the forth order Runge－Kutta method.To be more specific，two models were built under ideal and non－ideal conditions，respectively.In the first model，air resistance was neglected.A precession of the orbit of the ball was found.Moreover，the angle of precession would decrease with the increase of the obliquity of the cone.When the latter approaching aparticular value of approximately 55.6°，the precession vanished and the ball had an elliptic orbit.In the second model，the resistances were set to be proportional to velocity in view of the low velocity.According to the experiments，the motion of the ball was aperiodic due to the loss of energy，which was consistent with the real situation.

Key words：similar celestial movement；three－dimensional track；forth order Runge－Kutta method

作者简介：陈耿祥（1994－），男，福建泉州人，华中师范大学物理科学与技术学院2012级本科生.

收稿日期：2015－11－01；修改日期：2015－12－17

中图分类号：O313.2

文献标识码：A

文章编号：1005－4642（2016）03－0028－05

［责任编辑：郭 伟］