EMI滤波器网络最佳工作状态设计及其平面化实现
宋 峥 王世山
(南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016)
EMI滤波器网络最佳工作状态设计及其平面化实现
宋峥王世山
(南京航空航天大学江苏省新能源发电与电能变换重点实验室南京210016)
摘要EMI滤波器是抑制传导干扰的重要手段之一,受噪声源、负载阻抗影响,其工作性能往往不佳。为了改善这些不利影响,提出了一种带有阻抗失配网络的EMI滤波器网络设计方法,其可根据噪声源及负载阻抗的大小,将阻抗失配网络分为L型与C型两类,并通过选取合适的失配网络参数使噪声源与滤波器的输入阻抗和负载阻抗与滤波器的输出阻抗均满足一定的比例关系。EMI滤波器网络利用不同阻抗比例关系产生不同的反射损耗这一特性,对滤波器的最佳工作状态进行配置,使得滤波器在原有插入损耗的基础上增加其反射损耗,达到改善滤波器工作性能的目的。为了减小滤波器体积,将滤波器网络设计方法应用于平面环形EMI滤波器中,并通过实例测试验证其有效性与可行性。
关键词:反射损耗插入损耗阻抗失配网络EMI滤波器
0引言
随着电力电子变换器工作频率逐渐提高,电磁干扰和电磁兼容问题越发突出,电磁干扰(Electromagnetic Interference,EMI)滤波器作为抑制传导电磁干扰的有效手段,得到了国内外学者的广泛关注[1-3]。
EMI滤波器的噪声源和负载阻抗对其工作性能具有很大影响,但设计者在设计时不易获得噪声源和负载阻抗的相关信息。虽然可以分析出电网上指定处呈现高阻抗,但大多数EMI滤波器并不是工作在固定频率处,且电力电子设备(噪声源)的高频阻抗也很难得到,故实际EMI滤波器总是在阻抗失配条件下工作[1]。因此,假设滤波器的噪声源和负载阻抗均为50 Ω,在阻抗完全匹配条件下设计的EMI滤波器并不能满足噪声抑制需求[4,5]。
目前,在阻抗失配条件下,EMI滤波器的设计方法主要有两种:①根据不同噪声源和负载阻抗对EMI滤波器插入损耗的影响,选择合适的滤波器拓扑结构后完成滤波器元件参数选取[6];②通过选取合适的滤波电路,使得滤波器即使在“最坏情况”下其插入损耗值也不会小于设计时所给定的最小值[7]。文献[8,9]较为全面地分析了噪声源和负阻抗失配时EMI滤波器的工作特性,并提出了适用于EMI滤波器的拓扑结构选取原则,但在实际中噪声源阻抗是随频率的改变而变化;文献[1]中采用“P”匹配网络和“S”匹配网络使得滤波器处于“最坏情况”下进行设计,使得滤波器即使在噪声源阻抗和负载阻抗完全相同时,其插入损耗值也不会小于设计时所给定的最小值,但这种方法设计出的滤波器裕量太大,造成滤波器体积偏大。
由传输线理论可知,滤波器对噪声信号的损耗主要由插入损耗与反射损耗两部分组成[10-12],然而设计者在设计EMI滤波器时往往未将反射损耗列入考虑范围之内,但在噪声源和负载阻抗失配程度很大时,滤波器的反射损耗是不可忽略的。故在噪声源和负载阻抗不匹配条件下对EMI滤波器进行设计时,应保证滤波器在实际运行时不仅有较大的插入损耗同时也应具有较大的反射损耗。
因此,出于利用噪声源和负载阻抗不匹配对EMI滤波器工作性能影响的目的,本文提出了一种带有阻抗失配网络的EMI滤波器网络设计方法,该网络利用滤波器端口阻抗失配所产生的反射损耗对EMI滤波器的工作状态进行有效配置,改善滤波器的噪声抑制效果,并将所设计的网络应用于平面环形EMI滤波器中。
1滤波器网络设计原理
1.1滤波器网络
滤波器网络可认为是由失配网络和滤波器组成,其结构如图1所示。其中失配网络主要是由电阻与电感或电阻与电容组成,滤波器主要是由电感与电容组成。
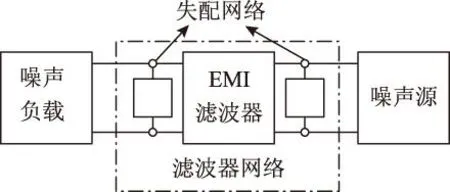
图1 滤波器网络结构Fig.1 Structure of EMI filter
此时,滤波器网络对EMI噪声的衰减可分为滤波器自身所带的插入损耗与接入失配网络后的反射损耗。
1.2插入损耗
插入损耗是滤波器重要的电气性能参数之一。EMI滤波器的插入损耗越高,对电磁干扰信号的抑制效果越好[1]。
如图2a所示,在待测设备与电源之间未接入滤波器时,测量得到的噪声源输出电压为V1;如图2b所示,当接入滤波器后,测量得滤波器输出电压为V2,则滤波器的插入损耗IL[5]为
(1)
式中,T为滤波器的传输矩阵,T11、T12、T21、T22均为T的元素;ZL为噪声负载阻抗;ZS为噪声源阻抗。
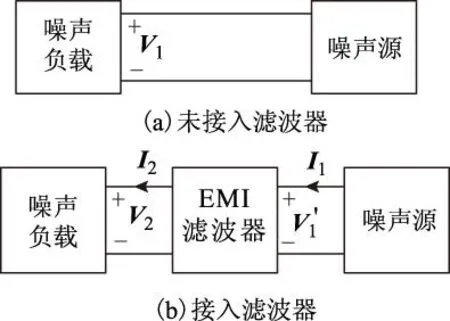
图2 插入损耗原理框图Fig.2 Schematic diagram of IL
1.3反射损耗
EMI滤波器的反射损耗是指在滤波器端口阻抗完全匹配时,设备接入滤波器前与接入滤波器后流经噪声负载的电流的比值[8]。
对于源阻抗ZS和负载阻抗ZL不等的电路,将一个入端特性阻抗Z1和Z2分别等于源内阻ZS和负载阻抗ZL的理想二端口网络接在源和负载之间,如图3所示。
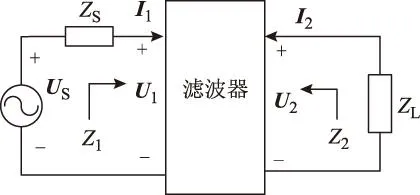
图3 接入滤波器后的电路Fig.3 Circuit with EMI filter
此时,滤波器对所流经电流无衰减作用,源端所能提供的功率全部被负载吸收,于是有
(2)
反之,当该电路未接此二端口网络时,流过负载的电流为
(3)
故可得EMI滤波器反射损耗A为
(4)
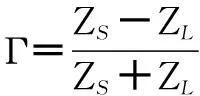
1.4失配网络
由基本的电路理论可知,任何不匹配的源阻抗和负载阻抗对EMI滤波器带来的不利影响都可以利用合适的失配网络来减弱或消除。如EMI滤波器因为电路谐振而导致插入损耗下降(可能会变成负值,即产生增益),此时可以使用简单的电阻作为失配网络,选择合适的电阻值即可消除谐振。但在滤波器输入、输出端口接入电阻会影响电路的工作性能,故选取适当的电容与电阻串联后并联或是选取电感与电阻并联后串联接入电路,使其主要在滤波器工作频率段内工作,其结构如图4所示。
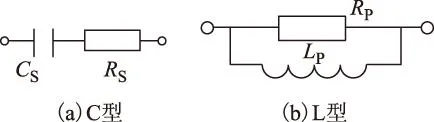
图4 失配网络基本结构Fig.4 Basic structure of mismatching network
为简单说明失配网络对滤波器噪声抑制性能的作用,本文在噪声源阻抗为低阻抗、负载阻抗为高阻抗的前提下,对接入失配网络与只接入滤波器两种情况进行定性分析,如图5所示。接入失配网络后,滤波器网络对噪声的抑制性能得到明显改善,由于失配网络中含有电容或电感元件,所以在低频段又增加了谐振频率点,但这种类型的谐振可由选取合适的电阻值来消除或减弱。
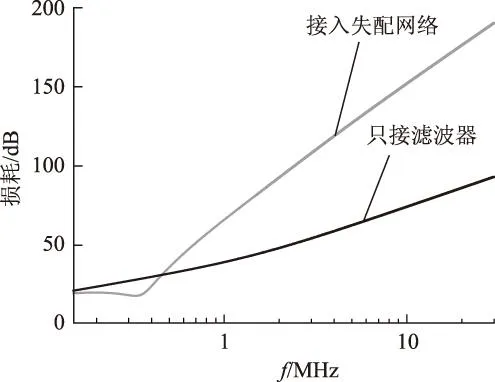
图5 失配网络与滤波器损耗Fig.5 IL of mismatching network and EMI filter
2最佳工作状态配置
滤波器网络工作状态的配置是以已知源阻抗和负载阻抗为前提,根据其源和负载阻抗值选择合适滤波器结构与失配网络对噪声进行有效抑制。
为保证滤波器插入损耗最大,可以根据不同源和负载阻抗情况选择相应滤波器结构,如图6所示[13]。低源阻抗与高负载阻抗应选择L-C型滤波器;高源阻抗与低负载阻抗应选择C-L型滤波器;低源阻抗与低负载阻抗应选择T型滤波器;高源阻抗与高负载阻抗应选择π型滤波器。

图6 滤波器结构Fig.6 Structure of EMI filter
以滤波器的负载阻抗为高阻抗、源阻抗为低阻抗为例,为更好地抑制EMI噪声,滤波器结构应选择为L-C型;同时,为了增加滤波器网络的反射损耗,应在其负载端串联接入L失配网络,源端并联接入C失配网络,其拓扑图如图7所示。
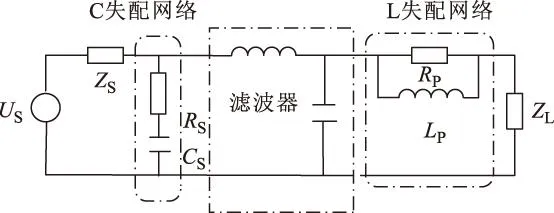
图7 滤波器网络拓扑Fig.7 Topological structure of EMI filter network
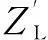
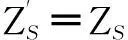
(5)
(6)
式中,ZC为C型失配网络阻抗;ZP为L型失配网络阻抗。
在不影响变换器正常工作性能的基础上,为增大滤波器网络的反射损耗,本文对失配网络对应元件的取值提出4个约束条件。
1)干扰源噪声抑制
针对干扰源端产生的EMI噪声,在滤波器自身插入损耗的基础上,通过接入C型失配网络以提供较大的反射损耗,确保噪声得到有效抑制,此时Z′S与从噪声源端看进去的最小输入阻抗应满足一定的失配比,即
(7)
式中,εC为失配比,表示接入C型失配网络后的端口阻抗与入端阻抗的比值,其取值范围通常为(0,1)。当εC取值越趋近于0,表示端口失配程度越大,对噪声的反射损耗也越大,此时工作电流受影响程度也越大;当εC取值趋近于1时,表示端口失配程度越小、匹配情况越好,即噪声将无损耗地完全传入滤波器中,此时将对滤波器自身的插入损耗产生较高要求,这种情况也通常被认为是滤波器工作的“最坏情况”,且失配比εC与反射系数Γ存在下列关系
(8)
由图7可知,当负载阻抗短接时,输入阻抗Z1将取得最小值,其表达式为
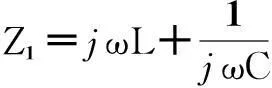
(9)
展开得
(10)
对Z1分母进行有理化得
(11)
式中,当ω较大时,Z1可化简为
(12)
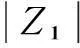
(13)
式中,ωL为滤波器工作频率下限处的角频率。
一般情况下,C型失配网络和源阻抗并联之后,阻抗的模值应小于C型失配网络自身阻抗模值,故式(13)可化简为
(14)
2)防止被其他设备干扰
为防止其他设备产生的EMI噪声传入源端,接入L型失配网络以提供较大的反射损耗,减轻滤波器的工作压力,此时Z′L与从负载端看进去的最大输出阻抗应满足一定的失配比,即
(15)
式中,εP与εC相似,为接入L型失配网络端口处的失配比。
由图7可知,当源阻抗开路时,输出阻抗Z2最大,其表达式为

(16)
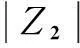
(17)

(18)
3)对工作电流无影响
为使有效信号能无衰减地通过EMI滤波器网络,接入的C型失配网络阻抗应尽可能大、L型失配网络的阻抗值应尽可能小,即CS的阻抗值要远大于RS值,LP的阻抗值则要远小于RP,如式(19)所示。
(19)
式中,ωf为变换器工作频率上的角频率。
4)利用电阻调节端口阻抗
在调节端口阻抗时,最佳措施是只接入电阻,这样既可达到调节阻抗的目的,也不会因为接入感性或容性元件而产生新的谐振,但在工程中不会使用这样的失配网络,因为其对工作信号损耗太大。故在滤波器不工作的频率段,失配网络应不起作用,如约束3所示;而在滤波器工作的频率段,失配网络中电阻能够起到调节阻抗的作用,即在滤波器工作频率下限fL上,CS的阻抗要小于RS,LP的阻抗则要大于RP,如式(20)所示。
(20)
根据上述4个约束条件,可以得出滤波器网络的设计步骤如下:
1) 确定源、负载阻抗性质,选择合适的滤波器结构。设计滤波器时,以能在全频率段提供噪声衰减需求的插入损耗确定滤波器元件的取值。
2) 确定εC和εP的大小。其值可根据噪声干扰情况选择,若干扰情况严重,则将εC和εP的值取小一些(如1/10),以获得较大的反射损耗;反之,则取大一些。
3) 确定失配网络对应元件值。由于失配网络中元件取值的约束条件均是用不等式给出,因此可以在满足不等式要求范围内随意选取元件值,但考虑经济性与体积等因素,CS与LP取值应尽可能小一些。
4) 若选取的εC和εP的值不合适而导致计算出的失配网络元件值不可能实现,则应换一组数据并重复步骤3。
为了更加直观地认识失配比对滤波器工作性能的影响,本文在ZS=0、ZL趋近于无穷大的情况下,分别取εP=εC=0.05、0.1、0.2、0.5,对其进行定性分析,如图8所示。失配比越小,其滤波器网络对噪声的抑制效果越好,但其失配网络对应储能元件取值往往也越大。

图8 失配比与滤波器网络损耗Fig.8 Relationship between mismatching ratio and IL of EMI filter network
3滤波器网络平面化实现
3.1EMI滤波器平面化
平面EMI滤波器的基本单元由差模电容单元、电感单元以及多接地电容单元组成,具有体积小和高频性能好等优点,其基本结构如图9所示[14-17]。其中,差模电容单元与多接地电容单元均采用高介电常数陶瓷材料表面镀银进行制作;电感单元则采用在PCB板上镀螺旋线圈并外接罐形磁心的方法实现[4-6]。
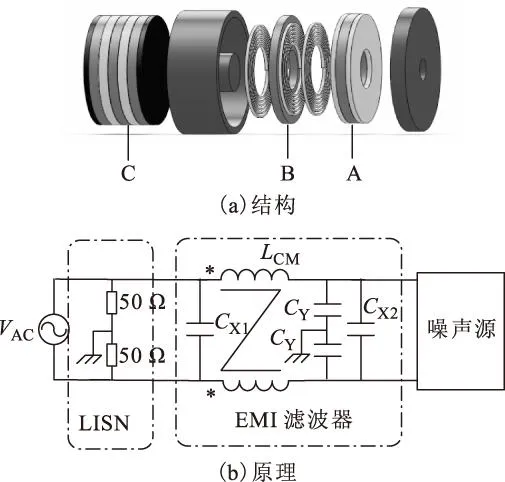
图9 平面EMI滤波器Fig.9 Planar EMI filter
由图9可看出,平面EMI滤波器中的A为差模电容单元,实现了拓扑结构中的差模电容CX1;B为电感单元,实现了拓扑结构中的共模电感LCM;C为多接地电容单元,实现了拓扑结构中共模电容CY与差模电容CX2。
出于安全接地考虑,EMI滤波器的共模电容值CY不能过大,必须首先确定,故设计平面EMI滤波器时应先确定共模电容值CY为
(21)
式中,n为所采用陶瓷片的数量;S为银层覆盖面积,由所流经的电流密度决定;εr和b1分别为陶瓷介质层的相对介电常数和厚度;空气的介电常数ε0=8.85×10-12F/m。
由转折频率与共模电容值可计算出共模电感值,此后由式(22)可确定电感单元的基本结构参数。
(22)
式中,le和Ae分别为有效磁路长度和面积,可通过磁心手册查询获得;真空磁导率μ0=4π×10-7H/m;μr为磁心的相对磁导率,也可通过磁心手册查表获得;N为集成LC结构中的线圈匝数n1和串联的铜箔线圈匝数n2之和。
具体实现共模电感平面化时主要从下面3个方面进行考虑:
1)匝间距。考虑单面线圈之间的绝缘以及寄生电容的影响,匝间距不能过小,同时受限于陶瓷介质板的面积,匝间距不能太大。根据以往经验,匝间距取0.6 mm较为合适。
2)线圈厚度。根据相关文献,LC线圈窄而厚的设计可以减少并联寄生电容EPC。由加工工艺所限,现阶段线圈厚度最大能做到0.08 mm。
3)线圈宽度。该值可根据应用场合所需流经电流的有效值与线圈厚度考虑一定裕量之后计算得到。
而在差模电路中,差模电感一般由共模电感的漏感提供,其经验公式为
(23)
式中,r1、r2分别为LC单元线圈的内、外半径;n1为电感单元的导线匝数;hΔ为漏感层的厚度;h为电感单元线匝的高度;μS为漏感层相对磁导率。
在获取差模电感之后,共模电容值可由转折频率与共模电容值共同确定,其平面化过程与共模电容类似。
3.2失配网络平面化
当完成失配网络对应元件取值时,为了失配网络平面化之后能与滤波器较好地组成一个完整的滤波器网络,失配网络平面化所采用电容的介质及电感的磁心应均与平面EMI滤波器结构相匹配,其实现方式如下:
1)失配电容。失配电容平面化过程与共模电容类似,其表达式均为
(24)
但式中S的取值有所区别,在共模电容中银层的覆盖面积等于陶瓷面积,而在失配电容中,由于失配电容取值的不确定性,故银层面积可能小于陶瓷面积。
2)失配电感。失配电感平面化过程与共模电感类似,其表达式均为
(25)
式中,N为失配电感中线圈匝数。
考虑到采用空气绝缘的机械稳定性差,本设计中失配电感与共模电感均采用薄的绝缘层提供机械支撑的交错绕组结构来减小绕组间的结构电容。
3) 失配电阻。失配电阻平面化过程较为简单,因平面EMI滤波器应用场合一般均为小功率系统,故可通过选取合适的贴片电阻,经物理焊接等方式接入平面EMI滤波器网络中,实现平面化,如图10所示。

图10 失配网络实物Fig.10 Picture of mismatching network
4网络滤波效果
4.1EMI滤波器
为了验证所提出带有失配网络EMI滤波器设计方法的可行性,本文以500 W、220 V/12 V的AC/DC变换器为实验平台进行验证。
根据未接入滤波器时所测的噪声与选取的噪声标准可计算出EMI滤波器的具体参数,如表1所示。

表1 平面EMI滤波器基本参数
根据上述参数完成平面EMI滤波器设计,电感单元与差、共模单元如图11所示。

图11 平面EMI滤波器基本结构Fig.11 Basic structure of planar EMI filter
在该变换器前接入平面EMI滤波器,对其做传导干扰测试,其结果如图12所示。测试显示,加入平面EMI滤波器后,对电磁干扰起到很好的抑制作用。
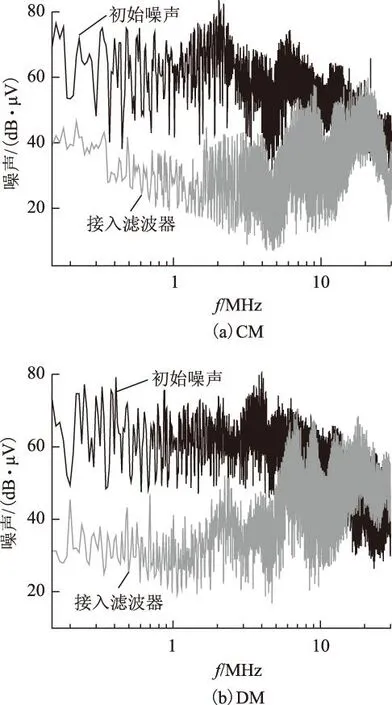
图12 只接入平面EMI滤波器测试结果Fig.12 Test result with planar EMI filter
4.2滤波器网络
确定了滤波器元件值后,根据第3节所提出的4个约束条件可知
(26)
由只接入平面EMI滤波器的实验结果可得,滤波器低频噪声抑制效果尚可,而高频噪声抑制效果较差,故取εC=εP=0.2;EMI滤波器的工作频率范围一般为0.15~30 MHz,但从接入滤波器后的噪声波形可看出低频段的噪声抑制效果较好,故为了设计更加准确,选取工作频率范围为1~30 MHz,变换器的工作频率为50 Hz。而为方便实现失配网络的平面化,失配电容取值应大于单片陶瓷片所能提供的电容值,并小于差模电容值;同理,失配电感应大于单根线圈接入磁心时所能提供的最小电感值,并小于共模电感值。故可采用二分法,先确定失配电容值与失配电感值,然后代入式(26)中,若能得到RS与RP的取值区间则完成计算,且应尽量取较小值,反之则重新进行迭代计算。
通过上述过程,可获得失配网络的取值参数如表2所示。

表2 失配网络基本参数
按上述参数完成设计后,在该实验平台前接入EMI滤波器,对其做传导干扰测试,其实物连接与测试结果分别如图13~图15所示。

图13 滤波器网络电路拓扑Fig.13 Topological structure of EMI filter network

图14 实物连接Fig.14 Linking of test circuit

图15 噪声抑制效果Fig.15 Effects of noise suppression
为更好地说明接入滤波器网络后噪声抑制效果得到较为明显的改善,现对只接入滤波器与接入滤波器网络之后的噪声抑制效果进行对比,具体步骤如下:
1)用只接入滤波器后的噪声,减去接入滤波器网络后的噪声,得到相对改善噪声值,如图16中曲线d所示。
2)分别求取共模与差模相对改善噪声值的上、下包络线,如图16中的曲线a、c所示。
3)求取上、下包络线的平均值,如图16中的曲线b所示。
从图16中的曲线b可以看出,对于共模噪声来说,在全频率段内,滤波器网络能够比只接入滤波器
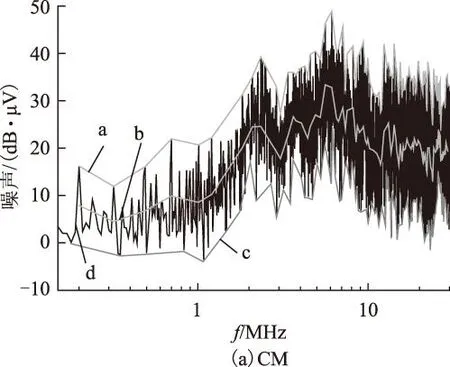
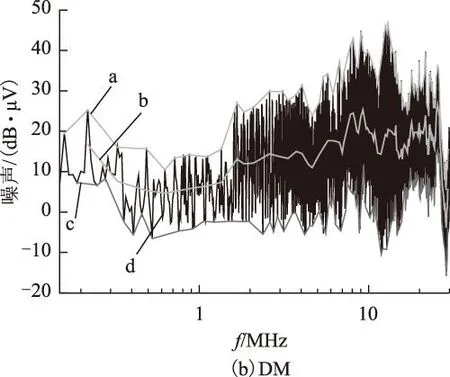
图16 噪声抑制效果说明Fig.16 Illustration of noise suppression
至少多提供5 dB的衰减量;对于差模噪声来说,在0.15~20 MHz频率段内,滤波器网络能够比只接入滤波器至少多提供6 dB的衰减量,而在20~30 MHz频率段内,可能由于高频寄生参数的影响使得滤波器网络的滤波效果反而比只接入滤波器效果差,对于该问题本课题组将在后续的工作中对其进行更加深入的研究。
5结论
本文以运行状态下EMI滤波器网络抑制效果为研究目标,在以插入损耗为基础完成EMI滤波器设计的前提下,针对其滤波效果不佳的现象,提出了以失配网络在EMI滤波器中的完善措施,得到以下结论:
1)提出了EMI滤波器网络一体化概念。本文所提出的滤波器网络是由“阻抗失配电路”与“EMI滤波器”构成。一般地,EMI滤波器设计是以在全频率段能提供满足噪声抑制需求的插入损耗为基础,并认为此时所设计的滤波器效果“最佳”,但当噪声源、负载阻抗不匹配时,则滤波器工作效果并不理想。此时,合适的失配网络选择能有效改善这一状况。
2)确定了两种类型失配网络——L型与C型,并得到两种类型网络对应元件的取值原则。失配电阻和失配电容串联组成了C型失配网络,该网络适用于与低阻抗的输入或输出端口并联,其电阻与电容的取值应使得并联后的端口阻抗与入端阻抗满足一定的失配比;失配电阻与失配电感并联组成了L型失配网络,该网络适用于与高阻抗的输入或输出端口串联,其电阻与电感的取值原则与C型失配网络类似。
3)将EMI滤波器网络设计方法应用于平面EMI滤波器中,实现了失配网络与滤波器的全平面集成,并得到高反射损耗和插入损耗,使得滤波器性能得到改善的基础上,体积也得到有效减小。
参考文献
[1]马伟明,张磊,孟进.独立电力系统及其电力电子装置的电磁兼容[M].北京:科学出版社,2007.
[2]钱照明,程肇基.电力电子系统电磁兼容设计基础及干扰抑制技术[M].杭州:浙江大学出版社,2000.
[3]Ozenbaugh R L.EMI Filter Design[M].California:Marcel Dekker Inc.,2001.
[4]Wang Shishan,Xu Chenchen.Design theory and implementation of a planar EMI filter based on annular integrated inductor-capacitor unit[J].IEEE Transactions on Power Electronics,2013,28(3):1167-1175.
[5]王世山,朱叶,周小林,等.圆环线匝构成的平面共模EMI滤波器的特性研究[J].电工技术学报,2011,26(11):68-73.
Wang Shishan,Zhu Ye,Zhou Xiaolin,et al.Characteristics research for planar common mode EMI filter based on toroidal LC coil[J].Transactions of China Electrochemical Society,2011,26(11):68-73.
[6]姜保军,孙力,赵克.EMI滤波器阻抗失配与EMI信号的有效抑制[J].电机与控制学报,2006,10(3):252-255.Jiang Baojun,Sun Li,Zhao Ke.EMI filter mismatching impedance and EMI suppression[J].Electric machines and control,2006,10(3):252-255.
[7]Luo Fang,Dong Dong,Boroyevich D,et al.Improving high-frequency performance of an input common mode EMI filter using an impedance mismatching filter[J].IEEE Transactions on Power Electronics,2014,29(10):5111-5115.
[8]Luo Fang,Boroyevich D,Mattavelli P.Improving EMI filter design with in circuit impedance mismatching[C]//Applied Power Electronics Conference and Exposition,Twenty-Seventh Annual IEEE,Orlando,FL,2012:1652-1658.
[9]刘超,张近民,王立欣.阻抗失配条件下信号EMI滤波器的设计[J].电子测量技术,2009,32(7):9-13.
Liu Chao,Zhang Jinmin,Wang Lixin.Design of signal EMI filter with mismatching impedance[J].Electric Measurement Technology,2009,32(7):9-13.
[10]王世山,朱叶,石磊磊.基于环形感容集成结构单元的平面EMI滤波器设计理论及实施[J].电工技术学报,2013,28(1):126-135.
Wang Shishan,Zhu Ye,Shi Leilei.Design theory and implementation of planar EMI filter based on annular integrated inductor-capacitor unit[J].Transactions of China Electrotechnical Society,2013,28(1):126-135.
[11]Wu Xiaofeng,Xu Dehong,Wen Zhiwei,et al.Design,modeling,and improvement of integrated EMI filter with flexible multilayer foils[J].IEEE Transactions on Power Electronics,2011,26(5):1344-1354.
[12]Wang S.Characterization and cancellation of high-frequency parasitic for EMI filters and noise separators in power electronics applications[D].Blacksburg:Virginia Tech University,2003.
[13]陈恒林,陈玮,冯利民,等.通过改变噪声源阻抗抑制高频共模噪声[J].电力电子技术,2006,40(6):124-125.
Chen Henglin,Chen Wei,Feng Limin,et al.High frequency common mode EMI noise suppression for switching converters by impedance control[J].Power Electronics,2006,40(6):124-125.
[14]Wu Xiaofeng,Wen Zhiwei,Xu Dehong,et al.Design and experiment research of integrated EMI filter based on flexible multi-layer foils[C]//International Power Electronics Conference,Sapporo,2010:2891-2896.
[15]Chen Rengang.Integrated EMI filters for switch mode power supplies[D].Blacksburg:Virginia Polytechnic Institute and State University,2004.
[16]Wang Shuo,Lee F C,Wyk J D.A study of integration of parasitic cancellation techniques for EMI filter design with discrete components[J].IEEE Transactions on Power Electronics,2008,23(6):3094-3102.
[17]Huang Huifen,Deng Liangyong,Hu Binjie.Techniques for improving the high-frequency performance of the planar CM EMI filter[J].IEEE Transactions on Electromagnetic Compatibility,2013,55(5):901-908.
宋峥男,1991年生,硕士研究生,研究方向为电力电子系统的电磁兼容。
E-mail:1136901614@qq.com(通信作者)
王世山男,1967年生,博士,副教授,研究方向为电力电子系统的电磁兼容、电气设备的多物理仿真技术。
E-mail:WSS.XJTU@163.com
The Design of the Optimized Running State of EMI Filter Network and Its Planar Realization
SongZhengWangShishan
(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and AstronauticsNanjing210016China)
AbstractElectromagnetic interference (EMI) filters play an important role in restraining conducted EMI. Affected by the impedance of the noise source and the load, the performance of the EMI filter is often poor. In order to eliminate the adverse effect, the design method of an EMI filter network with the impedance mismatching network is proposed in this paper. According to the value of the impedance of the noise source and the load, the impedance mismatching network will be classified into two kinds: the L-type network and the C-type network. By selecting the appropriate parameters of the impedance mismatching network, the noise source impedance and the input impedance of the EMI filter will meet some proportion, and the load impedance and the output impedance of the EMI filter will also meet some proportion. Using the characteristics that different impedance proportions have different values of reflection loss, the optimized running state of the EMI filter will be achieved. Besides the insertion loss, the reflection loss is also supplied by the EMI filter network and the performance of the EMI filter will be further improved. In order to reduce the volume of the EMI filter, the design method of the EMI filter network is applied to the planar EMI filter. Finally, an experiment is taken to verify the effectiveness and feasibility of the EMI filter network.
Keywords:Reflection loss,insertion loss,impedance mismatching network,EMI filter
作者简介
中图分类号:TM133
收稿日期2015-03-31改稿日期2015-06-29
国家自然科学基金(51177071)、南京航空航天大学研究生创新基地(实验室)开放基金(kfjj201412)及中央高校基本科研业务费专项资金资助。

