基于坐标变换的双馈风力发电机组叶片质量不平衡故障诊断
绳晓玲 万书亭 李永刚 成立峰
(1.华北电力大学电气与电子工程学院 保定 071003
2.华北电力大学能源动力与机械工程学院 保定 071003)
基于坐标变换的双馈风力发电机组叶片质量不平衡故障诊断
绳晓玲1,2万书亭2李永刚1成立峰2
(1.华北电力大学电气与电子工程学院保定071003
2.华北电力大学能源动力与机械工程学院保定071003)
摘要首先分析了叶片质量不平衡故障时双馈风力发电机组的电气特性,提出了基于dq坐标变换规则的定、转子电流特性分析法;然后采用希尔伯特解调法对电流信号进行处理,突出了电流的故障频率;最后在Matlab/Simulink环境下进行了仿真,并在双馈风力发电机组实验平台上进行了验证。结果表明,叶片质量不平衡故障时,发电机定、转子电流中都包含故障频率——叶片转频,该方法在叶片不平衡故障的识别中是有效的,具有一定的工程应用价值。
关键词:双馈风力发电机组叶片质量不平衡定、转子电流坐标变换
0引言
风能作为一种清洁、绿色的可再生能源,已成为世界各国新能源发展的重要方向[1]。随着风力发电机组装机容量的持续增加,如何降低机组维修成本和停机时间以及提高机组出力成为制约风力发电发展的关键问题[2,3]。
风电机组大多运行在环境比较恶劣的户外或海上,风沙的磨损或结冰沉积等会造成叶片质量不平衡;另外疲劳应力的作用会使叶片产生裂纹,灰尘、杂物、雨水等进入裂纹也会引起叶片质量的不平衡,并进一步加剧叶片和其他部件的疲劳和振动,若继续运行会对机组产生非常大的危害,严重时叶片断裂造成重大损失[4]。针对风机叶片质量不平衡问题,文献[5]建立了风机模型,利用有限元方法分析了叶片质量不平衡引起的机组振动特点。文献[6,7]在模拟实验平台上采集了机组振动信号进行频谱分析,结果显示质量不平衡情况下机组在水平方向的振动会增加。但振动信号的采集需要安装振动传感器,这首先增加了监测成本,其次对于安装在几十米高空的机舱很难进行实时监测。文献[8-10]则分析了叶片质量不平衡与发电功率的关系。由于功率的计算需要三相电流和电压,采集和计算都较麻烦,因此这些文献只分析了功率有效值或单相功率的变化,故分析结果难免偏颇。文献[11]分析了直驱风力发电机组叶片质量不平衡情况下发电机定子电流与轴转频的关系,利用定子电流信号间接分析转频变化特性来诊断叶片质量不平衡。文献[12]同样也是针对直驱风力发电机组,提出了利用定子电流信号模平方的方法来诊断叶片质量不平衡。
本文针对双馈风力发电机组叶片质量不平衡故障时发电机电气特性以及故障诊断等问题展开研究,找出了故障诊断依据,实现了故障的早发现早诊断,避免了重大事故发生,提高了机组运行效率。
1叶片质量不平衡机理分析
叶片质量不平衡故障可等效为在叶片上存在一个距离轮毂为R的不平衡虚拟质量块m[6,8]。等效不平衡质量块产生的重力矩会对风机的输出转矩产生影响[13],风机输出的机械转矩Tw可表示为
Tw=Tw0+mgRsin(ωwt+φw)
(1)
式中,Tw0为气动转矩;ωw为风机叶片旋转角速度;φw为叶片初始位置角度。
图1为风机某一叶片质量不平衡时的示意图。等效质量块m随着叶片以ωw的速度旋转,它产生的重力矩会造成风机主轴(也称叶片转子轴)转速的波动。如图1a所示,不平衡质量块由顶部向下旋转到底部的过程中会给主轴加速;而当该叶片由底部向上旋转到顶部的过程中,等效质量块的存在会给主轴减速,如图1b所示。这样的周期变化频率等于叶片转频[8]。另外文献[14,15]中也论证了当转矩周期性波动时,轴转速也会出现相同频率的波动。双馈风力发电机组通过增速齿轮箱将风机和发电机连接起来,发电机转子旋转角速度等于Nωw(N为齿轮箱的增速比)。风机主轴增速、减速的变化会反映到发电机转子速度上,使转子发生增速、减速的周期波动,波动频率等于叶片转频。
根据双馈风力发电机组的运动方程有[16]
(2)
式中,Te为风力发电机组的电磁转矩;ωr为发电机转子电角速度;ρ为极对数;J为机组的转动惯量。
将式(1)代入式(2),并令初相角φw=0,可求出转子电角速度ωr为
ωr=ωr0+ωrgcosωwt
(3)
式中,ωr0为气动转矩对应的转子电角速度;ωrg为转子速度周期波动幅值,ωrg=ρmgR/Jωw。
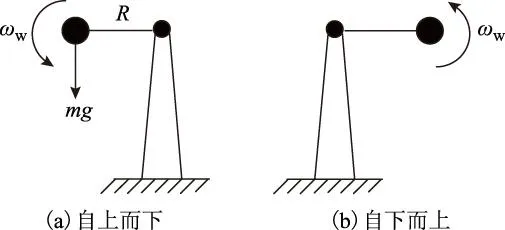
图1 叶片质量不平衡等效模型Fig.1 Equivalent model of blade mass imbalance
2双馈风力发电机组特性分析
2.1双馈风力发电机组工作原理
双馈风力发电机组的结构类似于绕线式感应电机,定、转子均为三相对称绕组,所不同的是转子绕组与一个三相励磁变换器相连,并在转子绕组中施以转差频率为sω1的三相对称电源,其中ω1为同步速。为了实现稳定的机电能量转换,定、转子旋转磁场必须均以同步速旋转,保持相对静止,因此稳定时各频率应满足如下关系[16]
ω1=ωr+sω1=ωr+ωz
(4)
式中,ωz为转子电流角频率;s为转差率。
当风力发电机组稳态运行时,ω1应等于电网电压角频率。在电网电压恒定的情况下,ω1可认为是一定值[16]。再结合式(3)和式(4)可得出质量不平衡时转子电流角频率ωz以及其瞬时相位θr分别为
ωz=ωz0-ωrgcos(ωwt)
(5)
(6)
式中,ωz0=ω1-ωr0。
2.2双馈风力发电机组转、定子电流分析
设ira为转子a相电流,并设其初始相角为零,则ira可表示为(推导过程见附录)
(7)
式中,Ir为转子a相电流的幅值。
由式(7)可知,在某一叶片存在质量不平衡时,转子励磁电流中除了频率为fz0的正弦分量外,还会出现频率为fz0±fw(ωz0=2πfz0,ωw=2πfw)的调制谐波分量。除此之外,调制电流的幅值为基波电流幅值的ωrg/(2ωw)倍,由式(3)可知,ωrg=ρmgR/(Jωw),对于大型风电机组,不平衡重力矩mgR远小于机组转动惯量J,而ωw一般大于1,故调制电流的幅值相比基波电流幅值是很小的。
为了进一步分析双馈发电机定子电流的特性,需首先将三相静止坐标系下的转子电流ira、irb、irc变换到d-q旋转坐标系下。根据abc-dq变换规则[17],转子d、q轴电流ird、irq计算过程见式(8)和式(9)。
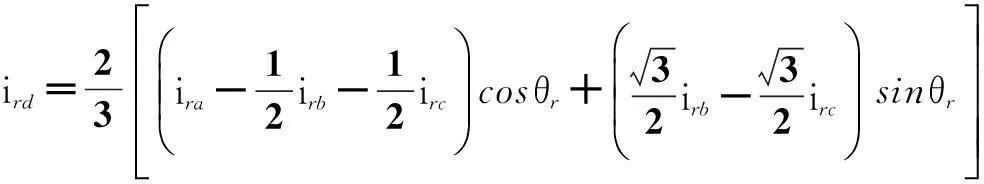
=ird0-irdw++irdw-
(8)
=irq0-irqw++irqw-
(9)
由式(8)和式(9)可知,转子励磁电流可以分解到3个d-q坐标系中,3个d-q坐标系的旋转速度分别是ωz0、ωz0+ωw和ωz0-ωw。其中以ωz0速度旋转的d、q轴电流分别为ird0、irq0;以ωz0+ωw速度旋转的d、q轴电流分别为-irdw+、-irqw+;以ωz0-ωw速度旋转的d、q轴电流分别为irdw-、irqw-。
根据双馈风力发电机组数学模型以及定子磁链定向原则有[16]
(10)
式中,ψsd和ψsq分别为定子磁链的d、q轴分量;ψs为定子磁链的幅值;isd和isq分别为定子电流的d、q轴分量;Ls为定子自感;Lm为定、转子间互感。
将式(8)和式(9)带入式(10)可得
(11)
也即定子的d、q轴电流可表达为
(12)
由式(12)可知,定子电流也能分解到3个旋转的d、q轴上,设3个d、q轴的转速分别为ω0、ω+和ω-,为了使定子磁场与转子磁场保持相对静止,应有ω0=ωz0+ωr0=ω1、ω+=(ωz0+ωw)+ωr0=ω1+ωw、ω-=(ωz0-ωw)+ωr0=ω1-ωw。故定子电流分解后的3个d、q轴转速分别为ω1、ω1+ωw和ω1-ωw。以ω1速度旋转的d、q轴电流分别为isd0、isq0;以ω1+ωw速度旋转的d、q轴电流分别为-isdw+、-isqw+;以ω1-ωw速度旋转的d、q轴电流分别为isdw-和isqw-。
根据dq-abc坐标变换规则以及式(8)和式(9)的推导过程,可得出发电机定子a相电流的表达式为
isa=Iscos(ω1t+φ0)-Is1cos(ω1t+ωwt+φ1)+
Is2cos(ω1t-ωwt+φ2)
(13)
式中
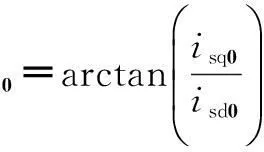
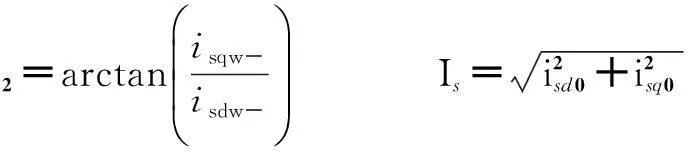
由式(13)可知,当某一叶片存在质量不平衡时,定子电流中除了频率为f1的基波外,还会出现频率为f1±fw(ω1=2πf1,ωw=2πfw)的调制谐波分量。同时在式(7)中也分析出来,转子励磁电流中也存在频率为fz0±fw的调制谐波分量,其中fw通常被称作故障频率或调制频率。由此便得出了利用定、转子电流诊断风力发电机组叶片质量不平衡故障的依据:定、转子电流中除了各自的基频外,还存在调制频率fw,该频率为风机叶片转频。
通过前述分析可知,定、转子电流的谐波幅值与基波电流相比非常小,因此直接分析电流的FFT(快速傅里叶变换)很难看出调制频率。而信号处理中的希尔伯特解调方法能够从信号中解调出低频的调制分量,因此在本文中通过对电流信号进行希尔伯特解调分析来提取故障频率。
3希尔伯特解调法
希尔伯特解调法通过希尔伯特变换的方法从信号中提取调制信号,分析调制函数的变化来提取故障特征,在机械振动信号及其故障诊断方面得到广泛应用,但在电气信号分析方面应用还较少。文献[18]曾将该方法应用于电机故障诊断。
若一连续的时间信号为x(t),其希尔伯特变换可看成是x(t)通过一滤波器的输出[18]
(14)
x(t)与其希尔伯特变换构成x(t)的解析信号Zt
(15)
由式(15)可得
(16)
式中,A(t)为幅值包络;θ(t)为相位包络;μ(t)为频率包络。
A(t)、θ(t)和μ(t)分别包含x(t)的幅值、相位和频率调制信息,对这些包络进行频谱分析便可得到调制频率,实现解调。
接下来以转子电流为例,按照上述步骤分析希尔伯特频率包络解调的过程。转子电流可表达为
(17)
求出ira的希尔伯特变换后,可得其解析信号为
(18)
式中,相位包络θ(t)可表示为
(19)
对θ(t)求导可得
(20)
将式(20)中的μ(t)去直流并进行FFT变换便可得到调制频率ωw,这就是希尔伯特变换的解调功能。同理也可求出定子电流的调制频率ωw。
基于希尔伯特变换的解调法能够分离出原信号中的调制信息进行解调,消除了原始信号的基频,只剩下调制频率,得到的结果比较清晰直观。
4仿真分析
4.11.5 MW机组仿真
为了验证前文所述理论分析的正确性,利用Matlab/Simulink模块,搭建了一个1.5 MW的双馈风力发电机组平台。平台模型结构如图2所示。仿真模型参数见表1,双馈风力发电机组转子侧采用定子磁链定向矢量控制[16]。
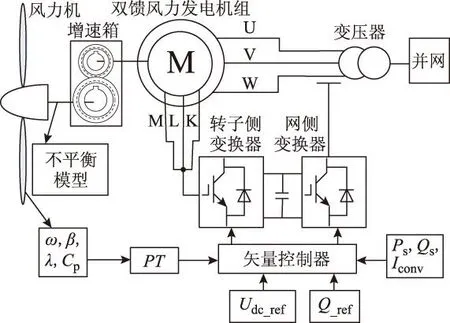
图2 仿真平台Fig.2 Simulation platform
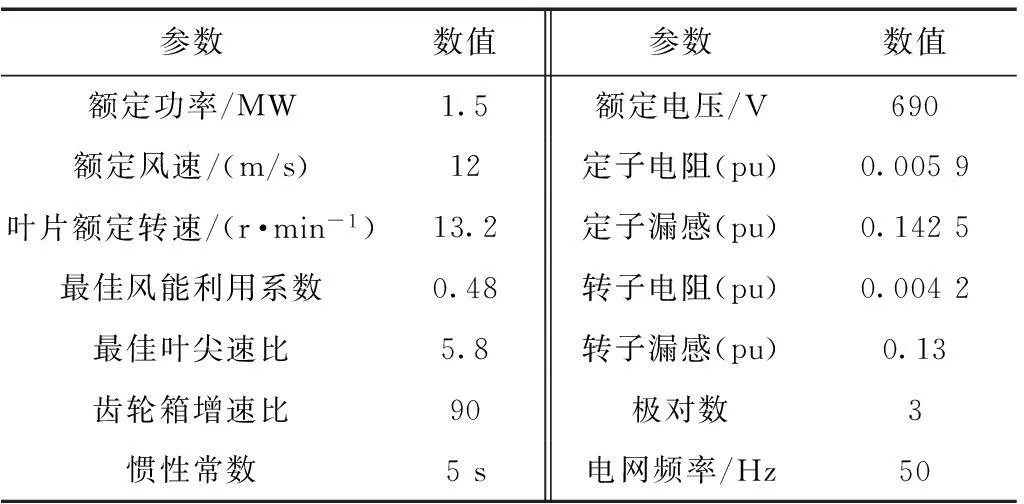
参数数值参数数值额定功率/MW1.5额定电压/V690额定风速/(m/s)12定子电阻(pu)0.0059叶片额定转速/(r·min-1)13.2定子漏感(pu)0.1425最佳风能利用系数0.48转子电阻(pu)0.0042最佳叶尖速比5.8转子漏感(pu)0.13齿轮箱增速比90极对数3惯性常数5s电网频率/Hz50
仿真前首先定义了不平衡度系数的概念,不平衡度系数b可表示为
(21)
式中,Twg为不平衡重力矩。
平台搭建好之后,首先进行了正常工况的仿真。然后在保证机组稳态运行的条件下,故障程度由低到高逐渐增加,分别进行了1%、3%、5%、8%和10%五种不平衡工况的仿真。为了便于对比,这五种工况下风机的运行参数相同,均为恒定风速10 m/s,叶片转速12.1 r/min。
图3为正常以及10%不平衡工况下叶片转速的对比图。从时域图3a可看出,在不平衡工况下叶片转速有明显的周期波动;经FFT变换后其频率为0.2 Hz,也即叶片转频(12.1/60≈0.2),如图3b所示。
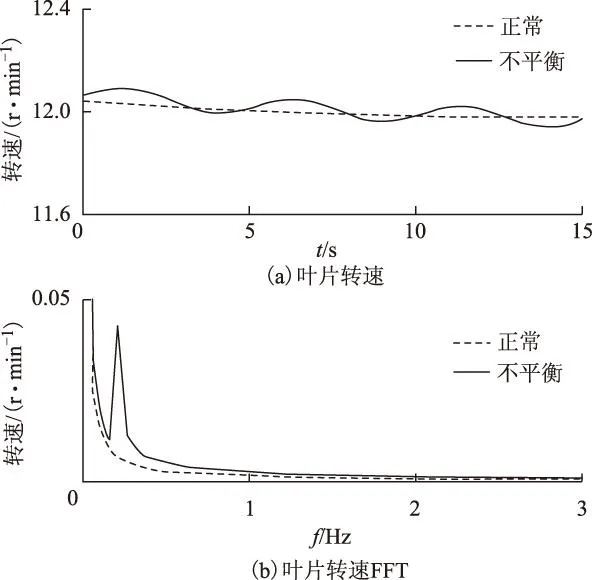
图3 正常及10%不平衡工况下叶片转速Fig.3 Blade rotate-speed of normal and 10% imbalance
图4为正常以及10%不平衡工况下定子电流仿真分析的结果。由图4a可知,正常以及不平衡工况下定子电流在时域图形上基本重合。在图4b中,正常及不平衡定子电流在50 Hz处几乎完全重合,将49.5~50.5 Hz频段的纵坐标放大几百倍后,才能看到二者的区别。图4c是对定子电流进行解调的结果:不平衡故障下的定子电流在叶片转频(即调制频率)0.2 Hz处有明显的峰值,而正常情况下的定子电流则没有。由此可见,希尔伯特包络解调可凸显故障频率,结果清晰直观。
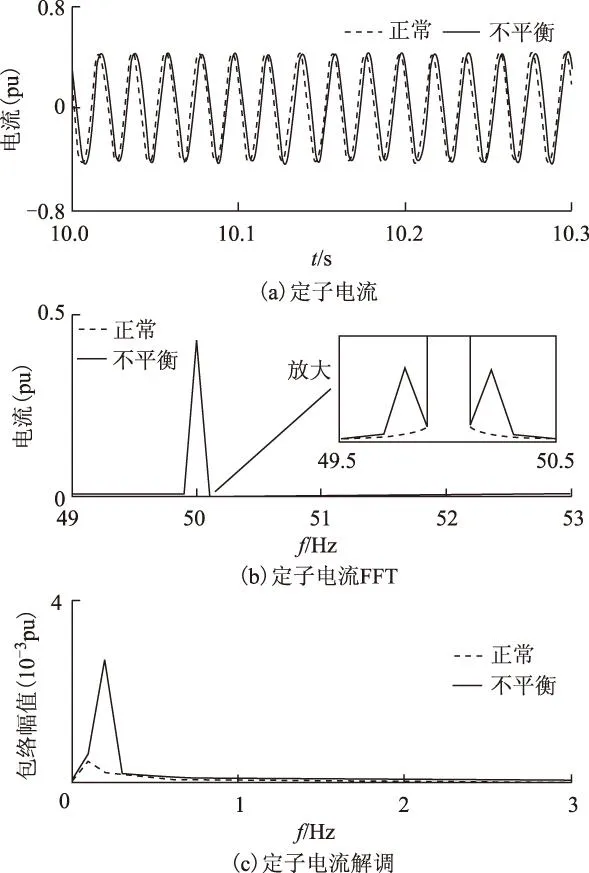
图4 正常及10%不平衡工况下定子电流Fig.4 Srator current of normal and 10% imbalance
图5为正常以及10%不平衡工况下转子电流仿真分析的结果。由图5a和图5b可知,正常以及不平衡时转子电流的基频均约为5 Hz,但与图4a中定子电流时域波形不同,在图5a中,正常及故障下的转子电流有明显相位差,这与前面式(6)的分析一致。由于转子电流基频较小,因此在故障前后转子电流的相位变化明显。而定子电流基频相对较大,因此在定子电流的时域波形图上看不出明显差别。不平衡转子电流中解调出叶片转频0.2 Hz,如图5c所示。
除此之外,对于其他几种不平衡工况下的定、转子电流也进行了相同的分析,结果与上述分析一致。图6为在1%、3%、5%、8%和10%五种不平衡工况下解调出的叶片转频0.2 Hz处所对应的幅值。从图6
中可看出,随着不平衡程度的增加,故障频率所对应的幅值也随着增加。
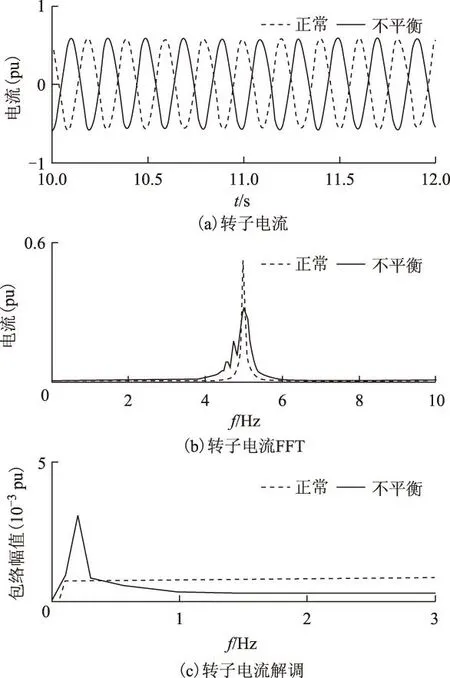
图5 正常及10%不平衡工况下转子电流Fig.5 Rotor current of normal and 10% imbalance

图6 各不平衡工况对应的故障频率幅值Fig.6 Amplitude of fault frequency for different degree of imbalance
4.2实验机组仿真
目前商业化的风电机组都越来越大型化,兆瓦级风机是当前主流,但对于实验室类型的风机来说,一般都是小型的。笔者所在课题组有一套11 kW双馈风力发电机组,它是某兆瓦级风机的缩比模型。为了将仿真和实验结果进行对比,利用Matlab搭建了一个11 kW实验机组的仿真模型。该仿真平台参数与实验室11 kW机组参数一致,具体见表2。

表2 11 kW DFIG仿真参数
平台搭建好之后,进行了正常工况和2.4%不平衡工况下的仿真,其中2.4%不平衡度工况对应1 kg不平衡质量块的实验(见后文实验部分)。仿真风况为恒定风速6.4 m/s,对应叶片转速75 r/min。仿真结果如图7和图8所示。

图7 正常及不平衡工况下定子电流Fig.7 Srator current of normal and imbalance
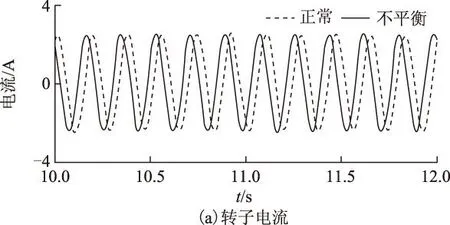

图8 正常及不平衡工况下转子电流Fig.8 Rotor current of normal and imbalance
由图7a可知,正常及不平衡情况下的定子电流在时域波形图上几乎完全重合;图7b是将48~52 Hz频段的纵坐标放大了近103倍后才看到二者的区别。由图7c可知,从不平衡的定子电流中解调出故障频率1.25 Hz(75/60=1.25),而正常情况下则没有,区别较明显。
与1.5 MW仿真类似,在图8a中,正常及不平衡的转子电流在时域图形上有相位差,但在图8b FFT频谱图中二者区别不大。在图8c中,不平衡转子电流中在1.25 Hz处有明显峰值。
5实验分析
为了进一步验证本文所提理论方法的正确性,在一个11 kW双馈风力发电平台上进行了实验。实验平台如图9所示。

图9 11 kW双馈风力发电实验平台Fig.9 Test platform of 11 kW doubly-fed wind turbine
该实验平台的工作原理是:三叶片风力机由调速电机(安装在风力机内部)拖动,模拟风速变化时叶片的旋转,从而带动主轴一起旋转。主轴通过增速齿轮箱与发电机相连。调速电机控制、变速恒频控制等都集成在主控柜中,如图9b所示。
发电机为绕线式异步发电机,参数见表2。为了模拟质量不平衡故障,在叶片上附加了一个重约1 kg(不平衡度b=2.4%)的质量块。为了防止对叶片表面造成损伤以及出于安全的考虑,将质量块用强力AB胶和若干条胶带固定在叶片内腔壁较平坦的地方,如图9a所示位置的内侧。
采集仪选用Yokogawa公司生产的DL850型示波记录仪,并采用型号为96001的钳式电流探头采集定子电流,而转子电流则选用HIA-C01型电流传感器采集,该传感器基于霍尔效应,适于低频信号。
实验参数:风力机设定为恒定风模式,叶片转速为75 r/min,转差率s为0.11,发电机并网运行。数据采集频率1 024 Hz,采样时间3 min,分别采集了机组正常工况和1 kg不平衡工况下的定、转子电流,并进行了分析。
图10为正常工况下采集的定、转子电流,图11为不平衡工况下的定、转子电流。首先对比图10与图11中的定子电流ia,基本看不出二者区别,这与仿真图7a是一致的。对这两种工况下的定子电流进行FFT分析,电流基频均为50 Hz,与图7b类似。再对比图10与图11中的转子电流,正常及不平衡工况下转子电流仍有相位差。在FFT频谱图中两者的基频均约为5.5 Hz,与图8b类似。
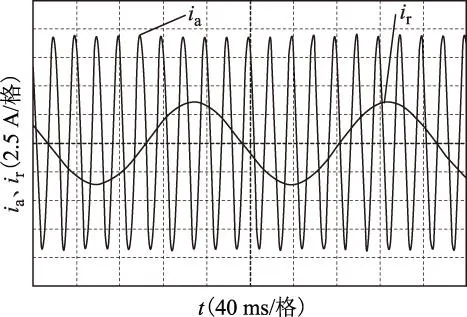
图10 正常定、转子电流Fig.10 Stator and rotor current of normal
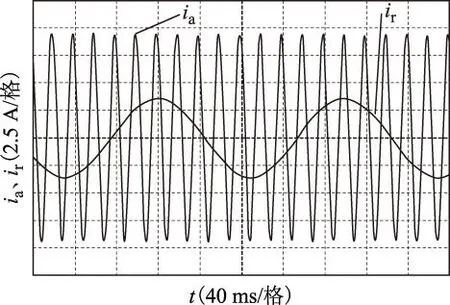
图11 不平衡定、转子电流Fig.11 Stator and rotor current of imbalance
图12为对正常和不平衡情况下采集的定、转子电流进行希尔伯特解调分析。从图12a中可看出,在不平衡的定子电流中解调出故障频率1.25 Hz;而在图12b中,则从不平衡情况下的转子电流中解调出故障频率1.25 Hz。

图12 定、转子电流解调Fig.12 Demodulation of stator and rotor current
对比11 kW机组仿真和实验结果可发现,定、转子电流的时域波形、FFT频域以及希尔伯特解调的结果都基本一致,不同之处主要是两种情况下电流的幅值有差别,这是因为仿真分析的电流是相电流,而实验时电流传感器采集的是线电流,这对分析结果影响不大。通过上述仿真和实验结果的分析验证了本文所提理论分析的正确性。
6结论
本文针对双馈风力发电机组叶片质量不平衡故障,从双馈发电机的数学模型出发,提出了基于dq坐标变换的定、转子电流特性分析法来诊断叶片不平衡故障,并采用希尔伯特解调法从电流信号中解调出故障频率,结果比较清晰直观。通过理论分析、仿真和实验分析得出以下结论:
1)叶片质量不平衡故障会导致双馈发电机定、转子电流中都包含以叶片一倍转频为调制频率的故障频率,并随着不平衡度系数的增加,故障频率对应幅值也增加,在一定程度上能够表征故障的严重程度。
2)除此之外,不平衡故障情况下转子电流与正常情况下相比其相位发生变化,这是转子电流频率存在波动所导致的。
基于双馈发电机定、转子电流特性来监测风机叶片的运行状态,及时消除引起不平衡的因素,防微杜渐,对于整个机组的安全、稳定运行具有重要的实际意义。
附录
式(7)的推导过程
ira=Ircosθr
式(8)和式(9)中sinθr的推导过程
注:在σ≪1时,cos(σ)≈1,sin(σ)≈σ。
参考文献
[1]GWEC.Global wind report annual market update 2011[R].Bonn:Global Wind Energy Council,2011.
[2]Hameed Z,Hong Y S,Cho Y M,et al.Condition monitoring and fault detetion of wind turbines and related algorithms:a review[J].Renewable and Sustainable Energy Reviews,2009,13(1):1-39.
[3]杭俊,张建忠,程明,等.风力发电系统状态监测与故障诊断技术综述[J].电工技术学报,2013,28(4):261-271.
Hang Jun,Zhang Jianzhong,Cheng Ming,et al.An overview of condition monitoring and fault diagnostic for wind energy conversion system[J].Transactions of China Electrotechnical Society,2013,28(4):261-271.
[4]蔡新,潘盼,朱杰,等.风力发电机叶片[M].北京:中国水利水电出版社,2014.
[5]Ramlau R,Niebsch J.Imbalance estimation without test masses for wind turbines[J].Journal of Solar Energy Engineering,2009,131(1):0110101-0110107.
[6]Jiang Dongxiang,Huang Qian,Hong Liangyou.Theoretical and experimental study on wind wheel imbalance for a wind turbine[C]//World Non-Grid-Connected Wind Power and Energy Conference,Nanjing,China,2009:351-355.
[7]Zhao Minghao,Jiang Dongxiang,Li Shaohua.Research on fault mechanism of icing of wind turbine blades[C]//World Non-Grid-Connected Wind Power and Energy Conference,Nanjing,China,2009:356-359.
[8]Xiang Gong,Wei Qiao.Simulation Investigation of wind turbine imbalance faults[C]//International Conference on Power System Technology,Hangzhou,China,2010:1-7.
[9]Caselitz P,Giebhardt J.Rotor condition monitoring for improved operational safety of offshore wind energy converters[J].Journal of Solar Energy Engineering,2005,127(2):253-261.
[10]杨涛,任永,刘霞,等.风力机叶轮质量不平衡故障建模及仿真研究[J].机械工程学报,2012,48(6):130-135.
Yang Tao,Ren Yong,Liu Xia,et al.Research on the modeling and simulation of wind turbine rotor Imbalance fault[J].Journal of Mechanical Engineering,2012,48(6):130-135.
[11]Xiang Gong,Wei Qiao.Imbalance Fault detection of direct-drive wind turbines using generator current signals[J].IEEE Transactions on Energy Conversion,2012,27(2):468-476.
[12]杭俊,张建忠,程明,等.直驱永磁同步风电机组叶轮不平衡和绕组不对称的故障诊断[J].中国电机工程学报,2014,34((9):1384-1391.
Hang Jun,Zhang Jianzhong,Cheng Ming,et al.Fault diagnosis of blade imbalance and winding asymmetry ofdirect-driven wind turbine with permanent magnet synchronous generator[J].Proceedings of the CSEE,2014,34(9):1384-1391.
[13]Niebsch J,Ramlau R,Nguyen T T.Mass and aerodynamic imbalance estimates of wind turbines[J].Energies,2010,3(4):696-710.
[14]Martin B,Pierre G,Bertrand R,et al.Models for bearing damage detection induction motors using stator current monitoring[J].IEEE Transactions on Industrial Electronics,2008,55(4):1813-1822.
[15]Yang Wenxian,Tavner P J,Wilkinson M.Wind turbine condition monitoring and fault diagnosis using both mechanical and electrical signatures[C]//International Conference on Advanced Intelligent Mechatronics,Xi’an,2008:1296-1301.
[16]贺益康,胡家兵,徐烈.并网双馈异步风力发电机运行控制[M].北京:中国电力出版社,2011.
[17]张波,颜湘武,王树岐.基于dq变换的三相电压暂降生成方法[J].电工技术学报,2011,26(10):55-61.Zhang Bo,Yan Xiangwu,Wang Shuqi.Method of three-phase voltage sag forming based on dq transformation[J].Transactions of China Electrotechnical Society,2011,26(10):55-61.
[18]赵妍,李志民,李天云.一种基于谱峭度的异步电机故障诊断方法[J].电工技术学报,2014,29(5):189-196.
Zhao Yan,Li Zhimin,Li Tianyun.A method for fault diagnosis of induction motor based on spectral kurtosis[J].Transactions of China Electrotechnical Society,2014,29(5):189-196.
绳晓玲女,1983年生,博士研究生,讲师,研究方向为风力发电机组的状态监测和故障诊断。
E-mail:sssxlyc@163.com(通信作者)
万书亭男,1970年生,教授,博士生导师,研究方向为大型火电机组、风力发电机组在线监测与故障诊断。
E-mail:13582996591@139.com
Fault Diagnosis for Blade Mass Imbalance of Wind Turbines with DFIG Based on Coordinate Transformation
ShengXiaoling1,2WanShuting2LiYonggang1ChengLifeng2
(1.School of Electrical and Electronic EngineeringNorth China Electric Power University Baoding071003China 2.School of Energy Power and Mechanical EngineeringNorth China Electric Power University Baoding071003China)
AbstractFirstly, the electrical characteristics of the doubly-fed induction generator (DFIG) under the blade imbalance fault are analyzed.Furthermore, the stator and rotor currents can be obtained according to the dq coordinate transformation.Then the Hilbert demodulation method is used to process the current signal so that the fault frequency can be highlighted.Finally, the simulation work under Matlab/Simulink and the experiment on the DFIG testing platform are taken for verification.It is shown that, the faulty stator and rotor currents contain the same harmonic component as that of the blade’s rotating frequency.The proposed method is effective to recognize the blade mass imbalance fault and therefore has an engineering application potential.
Keywords:Doubly-fed induction generator, blade, mass imbalance, stator and rotor current, coordinate transformation
作者简介
中图分类号:TM315
收稿日期2015-03-29改稿日期2015-07-02
国家自然科学基金(51177046)和中央高校基本科研业务费专项资金(12MS101,2014XS82)资助。

