基于滤波器状态反馈的矩阵变换器网侧电流闭环策略
陆 松 葛红娟 陈 思 徐媛媛 许宇翔
(南京航空航天大学新能源发电与电能变换重点实验室 南京 210016)
基于滤波器状态反馈的矩阵变换器网侧电流闭环策略
陆松葛红娟陈思徐媛媛许宇翔
(南京航空航天大学新能源发电与电能变换重点实验室南京210016)
摘要滤波器的引入降低了矩阵变换器轻载时的网侧功率因数,而滤波器的谐振特性更会导致系统不稳定。针对该问题,提出一种基于滤波器状态反馈的矩阵变换器网侧电流闭环控制策略,该策略以同步旋转坐标系下网侧电流为控制目标,并将滤波器状态变量的瞬时扰动引入电流环,对虚拟整流级电流矢量的期望值进行实时补偿,并根据补偿后的电流矢量期望值调制矩阵变换器。通过设置合理的反馈系数矩阵,滤波器的状态反馈使系统闭环极点移至更稳定的区域,增强了系统的稳定性。最后,实验结果表明该策略可以有效阻尼矩阵变换器动态过程的振荡,并能在全功率范围内使网侧保持较高功率因数。
关键词:矩阵变换器LC滤波器电流闭环状态反馈
0引言
矩阵变换器作为一种AC-AC变换器,因其结构紧凑、效率高、输入功率因数可调和理论上能实现任意频率输出等优点[1]受到众多学者的关注,尤其在电机驱动领域,安川电机成功研发的Varispeed AC和FSDrive-MX系列矩阵变频器[2,3],表明矩阵变换器开始迈入工业应用领域。近年来,研究人员更加关注矩阵变换器在其他领域的应用。如独立电源发电系统[4]、感应加热系统[5]和航空电源[6]等,以上研究成果都表明矩阵变换器具有良好的应用前景。
为满足电磁兼容性的要求,矩阵变换器与电源之间通常接有LC滤波器,防止高频电流毛刺反灌入电源。而在传统控制策略下,矩阵变换器的虚拟整流侧近似于开环控制,LC滤波器的引入带来了两个问题[7,8]:①因电容电流的存在,网侧电流发生相移,电源须提供大量无功功率;②LC滤波器为二阶欠阻尼系统,它的引入改变了原系统的动力学特性,可能降低矩阵变换器的动态性能,甚至使系统不稳定。针对上述问题,有不少文献进行了研究。文献[9]分析了网侧电流的相位偏差与系统参数的关系,提出依据系统参数计算出该偏差并在控制环节中予以补偿,使矩阵变换器运行于单位功率因数。文献[10]提出了三相静止坐标系下的网侧电流反馈控制,并在控制系统中增加相位补偿单元以消除控制量为正弦量而导致的稳态误差。但以上两种方法的准确性都依赖于对系统参数的准确辨识。文献[11]在文献[9]的基础上引入网侧功率因数角的正弦值作为反馈来进行PI调节,避免了对系统参数的依赖。文献[12]研究了dq坐标系下的网侧电流闭环控制,但误将输入侧的电流调制当作电压调制,因此控制上仍有误差。为了抑制LC滤波器的谐振,一般都在电感两端并联一个电阻以降低滤波器的输出阻抗,但系统的损耗却会因此增加。文献[13,14]将基于虚拟电阻的有源阻尼法应用于矩阵变换器,用控制回路中的额外算法替代了电路中的实际电阻,在不增加系统损耗的基础上有效抑制了滤波器的谐振。但文献[13]的控制系统复杂,计算量大,文献[14]的方法虽简明,但控制效果不佳。
以上的研究都只单独地针对滤波器引起的某个问题进行了讨论,没有全方面地考虑网侧滤波器对矩阵变换器稳态、动态性能的影响。因此,为同时解决滤波器带来的两个问题,本文研究了矩阵变换器网侧数学模型,给出了旋转坐标轴下的输入功率因数角的解析表达式。在文献[12]的基础上改进了旋转坐标系下的网侧电流反馈控制策略,以获得全功率范围内输入功率因数角的无静差控制。同时,将滤波器的状态变量引入控制环,利用状态反馈重新配置系统极点[15],达到抑制滤波器谐振,改善矩阵变换器动态特性的目的。
1矩阵变换器输入侧数学模型
本文以传统三相-三相矩阵变换器为例进行分析,该系统由电源、输入滤波器、开关矩阵和RL负载组成,如图1所示。图中,L、R和C分别为输入滤波器电感、电感寄生电阻和电容,LL和RL分别为负载电感与电阻。为方便分析,矩阵变换器输入侧电压、电流与网侧电压、电流在abc静止坐标系和dq同步旋转坐标系下的表示方法见表1。
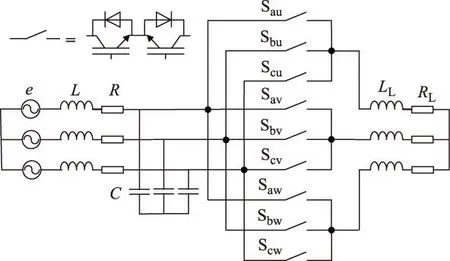
图1 三相-三相矩阵变换器Fig.1 Three-phase to three-phase matrix converter

输入侧变量abc坐标系dq坐标系网侧电压ea,eb,eced,eq网侧电流isa,isb,iscisd,isq矩阵输入侧电压va,vb,vcvd,vq矩阵输入侧电流ipa,ipb,ipcipd,ipq
设三相系统对称运行,则无需考虑零序分量的影响,三相-三相矩阵变换器系统可等效为三个独立的单相-单相矩阵变换器系统,其等效电路如图2所示,矩阵变换器可等效为受控电流源与受控电压源的组合,其大小与调制信号呈正比。
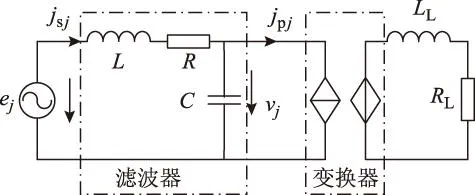
图2 矩阵变换器的单相等效电路Fig.2 Single-phase equivalent circuit for matrix converter
针对图2的等效电路,利用基尔霍夫定律,可知矩阵变换器输入侧有如下关系
(1)
取电感电流与电容电压为状态变量,电路在abc坐标下的状态方程可描述为
(2)
为便于设计dq同步旋转坐标系下的控制系统,需得到矩阵变换器输入侧在dq坐标系下的状态方程,设三相平衡电源为
(3)
式中,E为电网电压的有效值;ω为电网电压的角频率。本文中建立的旋转坐标系与电源电压同步,即有ed=2E/3,eq=0。
对式(2)进行坐标变换,可得矩阵变换器在同步旋转坐标系下的输入侧状态方程为
(4)
式中
从式(4)可以看出,矩阵变换器在dq坐标系是一个多输入多输出的耦合系统,输入量为矩阵变换器输入电流的dq轴分量,输出为网侧电流的dq轴分量。
2控制系统设计
2.1稳态控制
由式(4)得到矩阵变换器输入侧的方程为
(5)
(6)
矩阵变换器输入侧的控制对象为isd、isq,控制量为ipd、ipq,二者之间的关系为
(7)
因为dq轴分量都为直流量,稳态时各变量的微分都为零,令式(7)中微分量为零,得到dq轴下的稳态方程为
(8)
在传统控制策略下,矩阵变换器输入侧电流指令跟随电网电压,即ipq=0,可得该控制策略下的网侧电流为
(9)
式中,M1=1-ω2LC; M2=ωRC; M3=ωC。
可见,在传统的输入侧单位功率因数控制下,由于滤波器的存在,网侧电流的q轴分量大于零,其值随着功率的增大而减小。此时,实际功率因数角φ为
(10)
实际功率因数角与滤波器参数、电源频率和输出功率等因素相关。虽然通过式(10)可解出矩阵变换器输入电流指令,使网侧保持单位功率因数,但这种方法依赖于对系统参数的精确辨识,一旦系统参数因环境而发生改变,网侧势必无法保持单位功率因数,矩阵变换器将对电网注入大量无功功率。
因此,本文以id、iq为控制量,对网侧电流进行解耦控制,d、q轴控制器独立地控制网侧电流d、q轴分量,实现对网侧电流波形与相位的准确控制。id、iq的定义式为
(11)
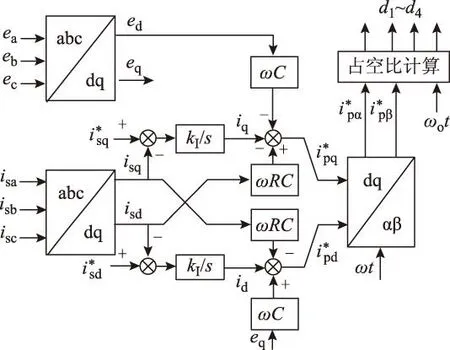
图3 网侧电流闭环稳态控制系统Fig.3 Closed-loop control strategy for steady state based on source current feedback
2.2动态控制
上述网侧电流闭环控制是依据矩阵变换器的稳态模型建立的,式(7)中的微分量全部被忽略为零,因此控制系统中未涉及动态性能的控制。此控制策略下的矩阵变换器动态特性完全由电路拓扑自身决定。
考虑式(4)中工作点微偏扰动,则相应的微偏扰动模型方程可描述为
(12)
输出方程为
(13)
式(12)可记为
系统特征方程为
(14)
解式(14)得系统的极点为
(15)
式中
系统的两对极点都为共轭复数,因为R为滤波器电感的寄生电阻,其值一般较小,故系统极点的实数部分远远小于虚数部分,系统的阻尼比几乎为零。动态过程将产生较长时间的振荡,网侧电流谐波大量增加。为抑制系统动态过程中的振荡,需要增加系统的阻尼。
由式(12)可得系统的能控性矩阵S为
Rank(S)=4,系统是状态完全能控的,因此可以通过状态反馈来任意配置极点,以此来改善系统的动态特性。
以本文的样机为例进行动态控制系统设计。矩阵变换器样机参数见表2。将表2的数据代入式(15)中,得到无状态反馈时系统的极点为
λ1,2=-25±6 769iλ3,4=-25±6 141i
为获得较好的动态特性,将系统的阻尼比配置为0.707,故可将极点左移至
求得反馈增益矩阵为
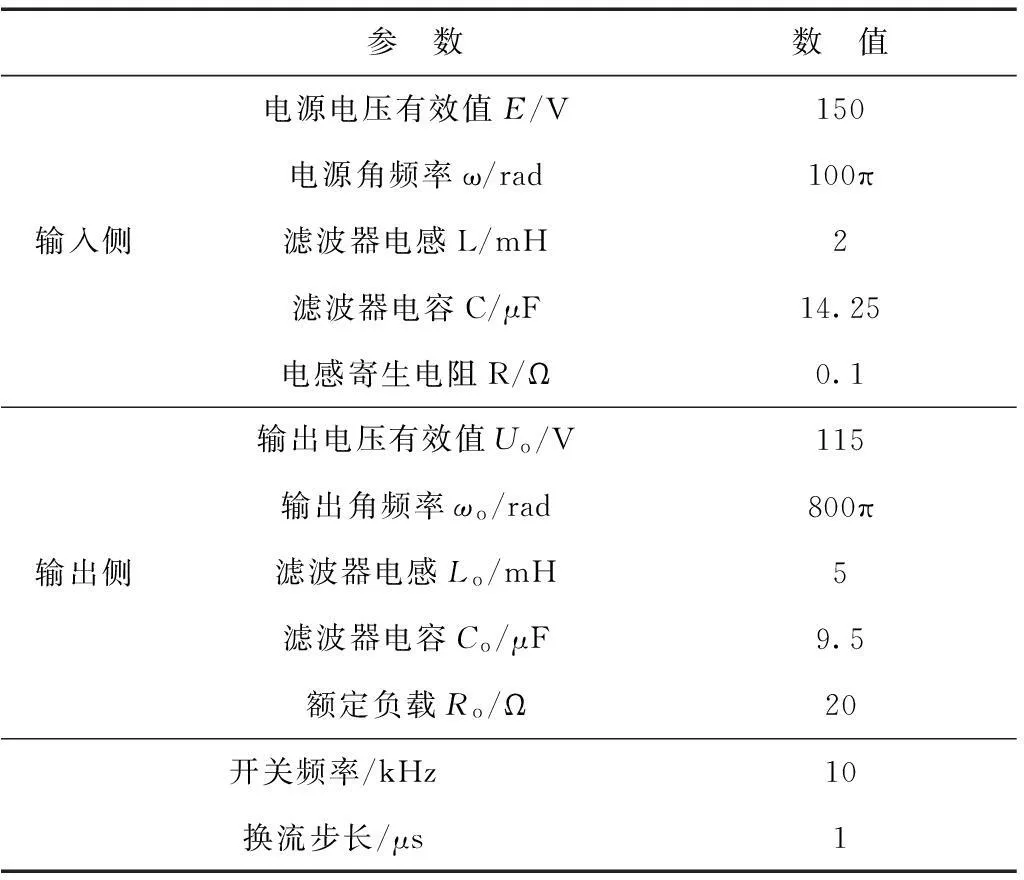
表2 实验平台参数
从求得的反馈增益矩阵可知,虽然dq轴变量耦合,但d轴的状态变量对d轴电路的控制效果远远大于q轴状态变量,对于q轴也同样如此。为了简化控制系统,可将反馈增益矩阵设置为
此时系统的极点为
λ″1,2=-6 587±6 736iλ″3,4=-6 380±6 142i
d、q轴的阻尼比分别为ξd=0.7和ξq=0.72, 系统将具有较好的动态特性。
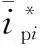
(16)
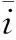
图4为基于滤波器状态反馈的矩阵变换器网侧电流闭环控制系统。为得到稳定的输出电压,增加输出电压反馈作为控制系统的外环;内环为功率环,网侧电流d轴有功分量由外环给定,q轴无功分量给定为零,以获取较高的功率因数;状态反馈作为内环的补偿,抑制动态过程产生的振荡。
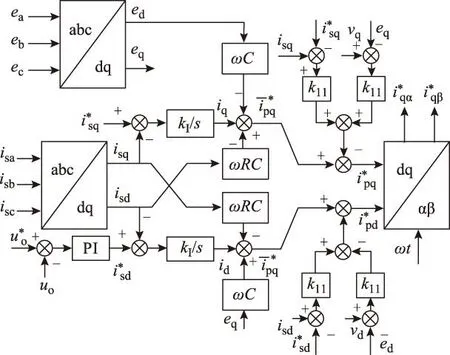
图4 基于网侧电流闭环与状态反馈的控制系统Fig.4 The control strategy based on grid current closed-loop and state feedback
3实验验证
为验证本文所提控制策略的有效性,搭建了以TMS320F28335+CPLD为控制核心,基于四步换流的2 kW三相-三相矩阵变换器实验样机,并以AC Source模拟电网,分别进行了稳态和动态实验,实验参数见表2。
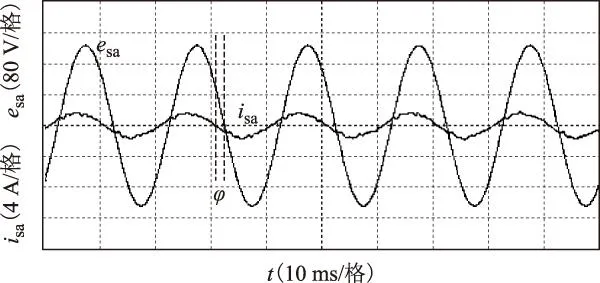
图5 开环控制下的电源电压与电流Fig.5 Source voltage and current based on open-loop control
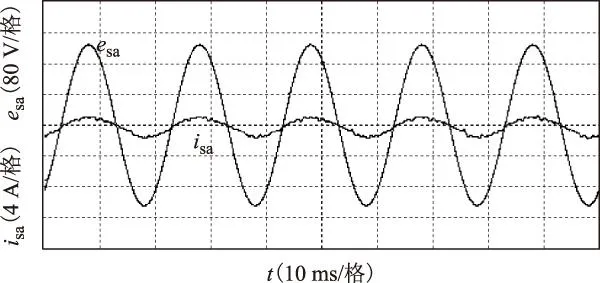
图6 闭环控制下的电源电压与电流Fig.6 Source voltage and current based on closed-loop control
图5为传统双空间矢量调制(策略①)下的稳态电源电压与电流,图6为本文所提网侧电流闭环控制(策略②)下的稳态电源电压与电流。图5和图6都是输出功率为20%额定功率(0.2 pu)时的稳态波形。与理论分析一致,在较小功率时,策略①下的电源电流将超前电源电压较大相位,图5中的相位差约为29°;而同样轻载的情况下,策略②下的电源电压与电流相位基本一致。
图7为两种控制策略下网侧功率因数角-功率曲线,可见传统双空间矢量调制下的矩阵变换器只有工作在额定功率附近才能保持较高的功率因数,轻载时电网须提供大量无功功率。在网侧电流闭环控制时,矩阵变换器无论在轻载还是重载时都能保持高功率因数。由于采样误差和控制延迟的存在,无法保证输入侧功率因数恒定为1,但功率因数角能保持在±3°以内。
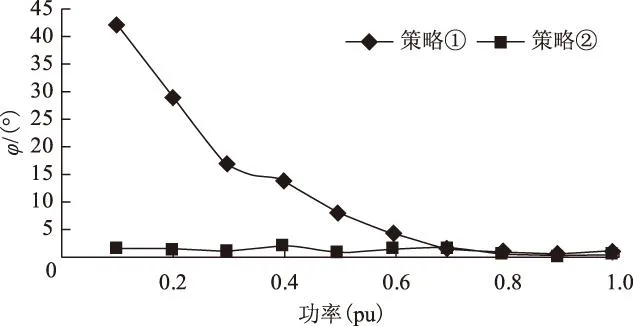
图7 不同功率下的输入功率因数角Fig.7 Power factor angle of input side in different power
图8为额定功率下三相稳态输出电压,三相电压都为115 V/400 Hz,呈平衡对称分布。将数据导入Matlab进行FFT分解,三相电压THD<2%。可见在本文控制策略下,矩阵变换器不仅能保持高功率因数电能输入,还能提供高质量的中频电能输出。
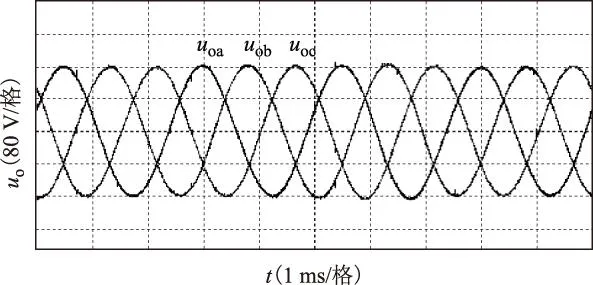
图8 三相稳态输出电压Fig.8 Three-phase output voltage in steady state
考虑到矩阵变换器应用于电源系统时负载的多变性,本文从负载突变研究矩阵变换器的动态系能。图9为采用图3所示稳态控制系统时的电压、电流波形,当负载突变时,由于控制系统中缺乏对动态振荡的抑制,系统只能依靠滤波电感的寄生电阻的阻尼而缓缓趋于稳定,网侧电流的振荡过程持续一个周期左右,振荡频率与滤波器的谐振频率一致。
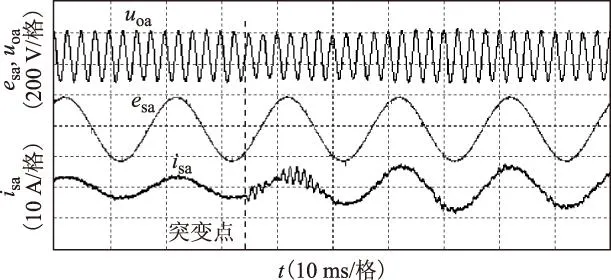
图9 无状态反馈时负载突变实验结果Fig.9 Experiment results when loads step up without state feedback
图10和图11为加入了状态反馈后的动态过程,负载由40 Ω突变为20 Ω时,输出电压突降20%,一个工频周期后快速恢复并稳定在115 V。当负载由20 Ω突变为40 Ω时,输出电压超调20%左右后快速恢复到115 V,网侧电流在两个过程中均平滑过渡,未发生振荡,表明本文所提控制策略成功增加了系统阻尼,抑制了动态振荡。
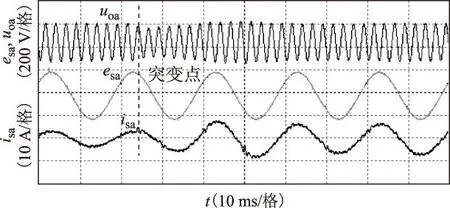
图10 加入状态反馈负载突增实验结果Fig.10 Experiment results when loads step up with state feedback
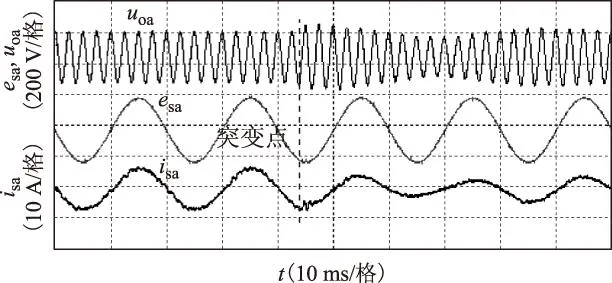
图11 加入状态反馈负载突减实验结果Fig.11 Experiment results when loads step downwith state feedback
4结论
本文研究了三相-三相矩阵变换器输入侧在三相静止坐标系和两相旋转坐标系下的数学模型,在此基础上提出了两相旋转坐标系下的网侧电流闭环控制系统,并合理地将状态反馈加入控制系统,使系统极点移动到更加稳定的区域。实验结果表明,本文所提控制策略能提高矩阵变换器轻载时的输入侧功率因数,同时能有效抑制动态过程中的振荡,减少网侧电流的谐波含量。
参考文献
[1]孙凯,周大宁.矩阵式变换器及其应用[M].北京:机械工业出版社,2007.
[2]Yamamoto E,Hara H,Uchino T,et al.Development of mcs and its application in industry [industry forum]([J].IEEE) Industrial Electronics Magazine,2011,5(1):4-12.
[3]Sawa T,Kume T,Hara H,et al.Power-electronics contributing to the green and clean world[C]//2011 IEEE 8th International Conference on Power Electronics and ECCE Asia (ICPE & ECCE),Jeju,South Korea 2011:11-18.
[4]Itch J,Takahashi H,Haruna J.A high energy saving interface system using a matrix converter between a power grid and an engine generator for bio diesel fuel[C]//2011 IEEE PowerTech,Trondheim,2011:1-7.
[5]NguyenQuang N,Stone D A,Bingham C M,et al.A three-phase to single-phase matrix converter for high-frequency induction heating[C]//13th European Conference on Power Electronics and Applications,EPE′09,Barcelona,2009:1-10.
[6]肖鲲,王莉娜,裴晓宇.多电飞机中双极矩阵变换器的改进控制方法[J].电工技术学报,2011,26(增1):8-14.
Xiao Kun,Wang Lina,Pei Xiaoyu.Research on modulation strategy for two-stage matrix converter in more electric aircraft[J].Transactions of China Electrotechnical Society,2011,26(S1):8-14.
[7]粟梅,孙尧,覃恒思,等.矩阵变换器输入滤波器的多目标优化设计[J].中国电机工程学报,2007,27(1):70-75.
Su Mei,Sun Yao,Qin Hengsi,et al.An multi-objective optimized of input filter of matrix converter[J].Proceedings of the CSEE,2007,27(1):70-75.
[8]Dasgupta A,Sensarma P.Filter design of direct matrix converter for synchronous applications[J].IEEE Transactions on Industrial Electronics,2014,61(12):6483-6493.
[9]陆晓楠,孙凯,李刚,等.双级矩阵变换器网侧功率因数的控制方法[J].电工技术学报,2010,25(10):108-114.
Lu Xiaonan,Sun Kai,Li Gang,et al.Control method analysis of grid side power factor in two stage matrix converter[J].Transactions of China Electrotechnical Society,2010,25(10):108-114.
[10]宋卫章,钟彦儒,李洁.带相位补偿环节的双级矩阵变换器网侧电流闭环控制[J].电工技术学报,2010,25(7):77-84.
Song Weizhang,Zhong Yanru,Li Jie.Input current feedback control strategy with phase compensation component for two-stage matrix converter[J].Transactions of China Electrotechnical Society,2010,25(7):77-84.
[11]Nguyen H M,Lee H H,Chun T W.Input power factor compensation algorithms using a new direct-SVM method for matrix converter[J].IEEE Transactions on Industrial Electronic,2011,58(1):232-243.
[12]Kwak S.Indirect matrix converter drives for unity displacement factor and minimum switching losses[J].Electric Power Systems Research,2007,77(5):447- 454.
[13]粟梅,孙尧,覃恒思,等.一种改善矩阵变换器系统动态性能和稳定性的控制方法[J].电工技术学报,2005,20(12):18-23.
Su Mei,Sun Yao,Qin Hengsi,et al.Effect of the input filter on stability of matrix converter drive system[J].Transactions of China Electrotechnical Society,2005,20(12):18-23.
[14]Wang X,Lin H,Feng B,et al.Damping of input lc filter resonance based on virtual resistor for matrix converter[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE),Raleigh,NC,2012:3910-3916.
[15]Dannehl J,Fuchs F W,Thogersen P B.PI state space current control of grid-connected PWM converters with LCL filters[J].IEEE Transactions on Power Electronics,2010,25(9):2320-2330.
陆松男,1990年生,硕士,研究方向为电力电子与电力传动。
E-mail:lusongsama@formail.com(通信作者)
葛红娟女,1966年生,教授,博士生导师,研究方向电力电子技术及电机控制。
E-mail:allenge@nuaa.edu.cn
A Grid Current Closed-Loop Control Strategy for Matrix Converter Based on States Feedback of Filter
LuSongGeHongjuanChenSiXuYuanyuanXuYuxiang
(Key Laboratory of New Energy Power Generation and Electrical Energy Transformation Nanjing University of Aeronautics and AstronauticsNanjing210016China)
AbstractThe use of the input filters usually results in the decreasing of the input power factor (IPF), especially under light-load condition. And the system stability is also influenced by the resonant characteristics of the LC filter. To solve these problems, a grid current closed-loop control strategy based on states feedback of the filter for the matrix converter is proposed. As the control targets in this scheme, the gird currents in synchronous reference frame are the feedback of current loop. Besides, the transient disturbances of filter state variables are also added to compensate the current vector reference of virtual rectifier. According to this current vector reference, matrix converter is modulated. By designing a proper state feedback gain matrix, the closed-loop poles of the system are shifted to a more stable area, which enhances the system stability. Finally, experimental results show that the oscillation of dynamic process is damped effectively and a high power factor is attained at full power range.
Keywords:Matrix converter,LC filter,current closed-loop,state variable feedback
作者简介
中图分类号:TM46
收稿日期2014-08-19改稿日期2014-10-27
国家自然科学基金(U1233127)和航空科学基金(2012ZC52034)资助项目。

