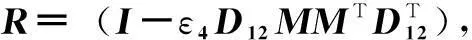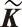磁悬浮永磁直线电动机控制系统非脆弱鲁棒控制的研究
蓝益鹏 陈其林 胡学成 刘宇菲
(沈阳工业大学电气工程学院 沈阳 110870)
磁悬浮永磁直线电动机控制系统非脆弱鲁棒控制的研究
蓝益鹏陈其林胡学成刘宇菲
(沈阳工业大学电气工程学院沈阳110870)
摘要由于磁悬浮永磁直线电动机控制系统存在参数变化、扰动的不确定性以及控制器参数的摄动,因此对该电动机控制系统提出非脆弱鲁棒控制,以实现数控机床磁悬浮永磁直线电动机驱动系统的精密控制。建立包含磁悬浮永磁直线电动机参数摄动和外界干扰的状态空间模型;基于Riccati不等式,推导出满足非脆弱鲁棒性能指标的H∞控制器的解析表达式;在Matlab环境下对控制系统进行仿真研究,仿真结果表明磁悬浮永磁直线电动机控制系统对参数和扰动的不确定性以及对控制器参数摄动具有鲁棒性,实验结果验证了该控制方法的有效性。
关键词:磁悬浮永磁直线电动机控制系统非脆弱鲁棒控制
0引言
磁悬浮永磁直线电动机是在永磁直线电动机的基础上设计的特种直线电动机,以实现数控机床伺服系统加工过程中的直接驱动与无摩擦进给。由于取消了中间环节以及处于磁悬浮运行方式,电动机本身更容易受到自身参数变化和外部扰动的影响,即对不确定性的影响更加敏感[1-3],因此,如何设计控制器来保证电动机的稳定运行显得尤为重要。
数控机床磁悬浮永磁直线电动机控制系统通常是一个高精度的运动控制系统[4,5],不仅要求电动机在磁悬浮和直接驱动运行过程中对参数摄动和外界干扰具有良好的抑制作用,为了保证足够的加工精度和表面粗糙度,对控制器自身参数的摄动也要具有良好的鲁棒性[6,7],即要求整个系统是一个非脆弱鲁棒控制系统。
本文提出一种非脆弱鲁棒H∞控制方法,建立了包含磁悬浮永磁直线电动机参数摄动和外界干扰的状态空间模型,推导出非脆弱H∞鲁棒控制器的解析表达式。对控制系统进行了仿真研究和部分实验研究。这对进一步提高数控机床伺服系统的性能具有重要意义。
1磁悬浮永磁直线电动机的状态空间数学模型
磁悬浮永磁直线电动机进给系统的数学模型可描述为[8]
(1)
式中,Fd为端部效应力;Fl为负载阻力;v为动子线速度;Rs为动子电阻;L为d、q轴电感;Ψf为永磁体基波励磁磁链;np为极对数;Kf为电磁推力系数;uq、iq分别为q轴动子电压和电流。
令
由于电动机中电枢回路电流引起电阻温度上升,导致Rs发生变化,并且磁路饱和程度不同,引起电感L发生变化,且永磁体充磁的不均匀性,特别是悬浮高度不同,导致Ψf发生变化。因此需要考虑参数摄动问题的数学模型改写为
(2)
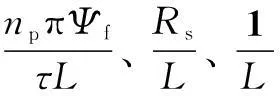
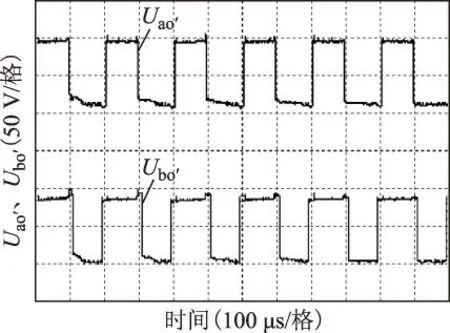
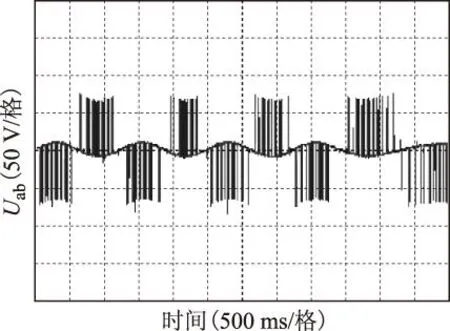
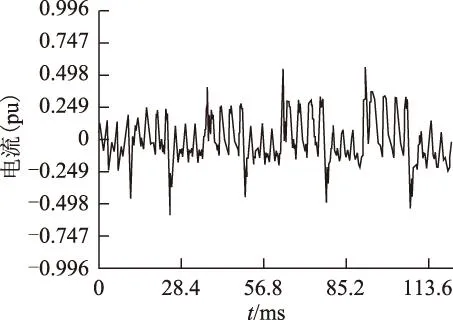
2磁悬浮永磁直线电动机非脆弱鲁棒H∞控制的描述
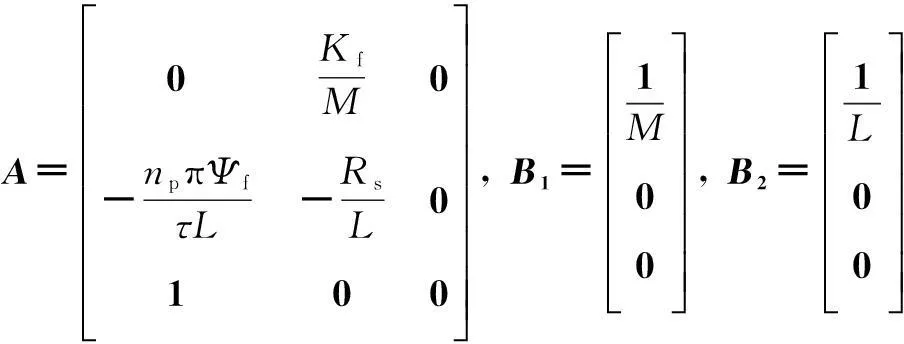
将式(2)简写为
(3)
式中,A、B1、B2、C1、D12均为已知矩阵;ΔA、ΔB为参数摄动矩阵,且
[ΔA,ΔB]=EΣ[Fa,Fb]
(4)
式中,E、Fa、Fb均为已知常数矩阵;Σ为未知矩阵,且Σ∈Ω, ΣTΣ≤1。
C1、D12为加权系数矩阵,分别为
考虑控制器摄动针对系统(3)设计的控制器为

(5)
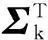
将控制器(5)代入ΔA、ΔB的表达式中,整理得
(6)
式中
Ak=A+B2(K+ΔK), ΔAk=EΣFk
Fk=Fa+Fb(K+ΔK), Ck=C1+D12(K+ΔK)
(7)
从扰动w到评价函数z的传递函数为
(8)
3磁悬浮永磁直线电动机非脆弱鲁棒H∞控制器的设计
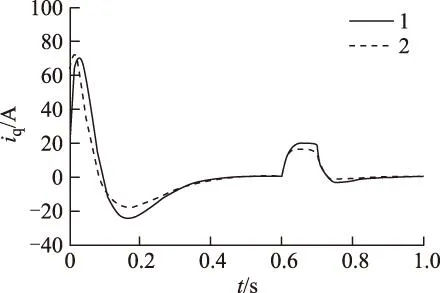
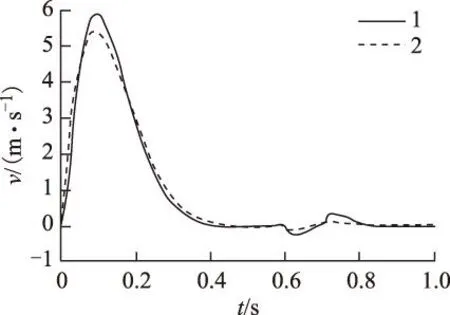
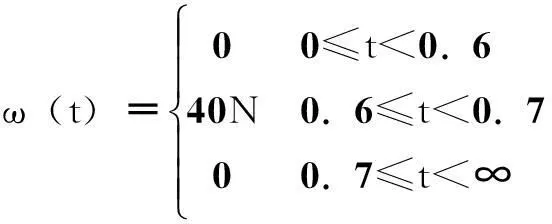
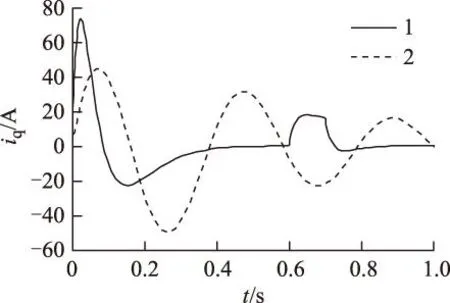
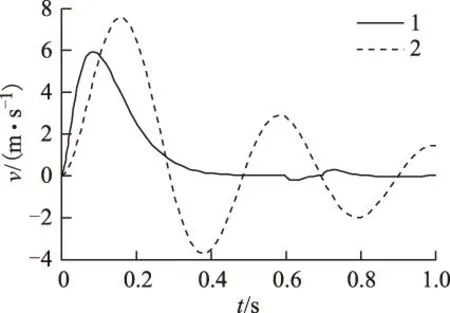
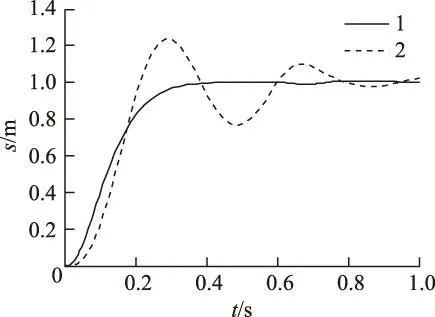
引理1[9]:对于任意矩阵M、N、E和F(FTF HFE+ETFTHT≤ε-1HHT+εETE (9) 引理2[10]:对于任意适当维数的矩阵M、N、E和F(FTF>1),对于任意常数ε>0, 则式(10)成立 (M+HFE)TX-1(M+HFE)< MT(X-ε-1HHT)M+ε-1EET (10) 定理:对于给定的被控对象(3),存在非脆弱状态反馈控制器式(5),使得式(8)对于任意的Σ∈Ω都成立的充分必要条件是:对于任意常数ε1、ε2、ε3、ε4均大于0,Riccati不等式为 (11) 存在正定解X,则闭环系统内部稳定,且满足H∞鲁棒性能准则。相应的控制器表达式为 (12) 证明: 1)必要性 由H∞性能指标与Riccati不等式的等价性,存在适当的正定矩阵X使式(13)成立。 (13) 将式(7)代入式(13)得到 X[A+ΔA+(B2+ΔB)(K+ΔK)]+ [A+ΔA+(B2+ΔB)(K+ΔK)]TX+ (14) 整理得 ATX+XA+(B2K)TX+XB2K+X(ΔA+ΔBK)+ (ΔA+ΔBK)TX+XB2ΔK+(B2ΔK)TX+XΔBΔK+ [(C+D12K)+D12ΔK]<0 (15) 考虑引理1和引理2,将式(15)进一步整理得 (16) (17) 式(17)两边同时加上 得到 (18) 式中 (19) 当S=0,控制器K的表达式为 (20) 相应Riccati不等式为 (21) 2)充分性 假设存在任意常数ε1、ε2、ε3、ε4>0,使得Riccati不等式(21)成立且存在正定解X,构造如式(20)的状态反馈控制器,恒等式 因此不等式 4仿真与实验结果 4.1磁悬浮永磁直线电动机非脆弱鲁棒控制仿真研究 磁悬浮永磁直线电动机的参数:动子质量M=50 kg,动子电阻Rs=1.687 8 Ω,d、q轴电感相等均为L=25.92 mH,极对数np=3,永磁体基波励磁磁链Ψf=0.175 4 Wb,极距τ=33 mm。当悬浮高度在0~2.5 mm之间变化时,对样机进行实际测试得到参数摄动最大值为:Δ1=7.5%,Δ2=12.5%,Δ3=10%。 取摄动形式的矩阵Σk为 图1 电流响应曲线Fig.1 Current response curve 图2 速度响应曲线Fig.2 Speed response curve 图3 位移响应曲线Fig.3 Displacement response curve 由图可知,设计的非脆弱的H∞鲁棒控制器使闭环系统在0.4 s时达到稳定状态,且位移无超调。当控制器产生摄动增益时,闭环系统同样可在0.4 s时趋于稳定,电流响应曲线和速度响应曲线无太大变化,位移响应曲线与摄动前相比基本一致,表明系统对控制器参数变化有鲁棒性。 4.2磁悬浮永磁直线电动机非脆弱鲁棒控制与PI控制的仿真对比 将非脆弱鲁棒控制与PI控制方法进行对比,在0.6 s时突加外部扰动,在0.7 s时卸去扰动,得到电流、速度和位移响应曲线如图4~图6所示,图中1线为非脆弱鲁棒控制,2线为PI控制。受到参数摄动的影响,PI控制方法在尚未完全进入稳态的情况下,非脆弱鲁棒控制已能较好地实现对系统的控制作用,即对不确定性的影响具有鲁棒性。 图4 电流响应曲线Fig.4 Current response curve 图5 速度响应曲线Fig.5 Speed response curve 图6 位移响应曲线Fig.6 Displacement response curve 4.3磁悬浮永磁直线电动机的实验结果 图7 磁悬浮永磁直线电动机控制系统Fig.7 The control system of magnetic levitation permanent magnet linear motor 速度参考值对应的标幺值为:Speedref=0.1,对应于0.8 Hz,周期1.25 s,速度52.8 mm/s。直流母线电压Ud=80 V。此时,对直流中性点o′的相电压Uao′和Ubo′波形如图8所示,相电压只有±Ud/2两个电平,即+40 V和-40 V。线电压波形如图9所示,Uab=Uao′-Ubo′。 Uab线电压波形有±Ud和0三个电平,即±80 V和0 V,图9的波形中相对宽的地方是减速反向过程,与理论分析结果一致。空载起动时,用示波器测量电动机的A相电流波形如图10所示,与电动机动态过程分析一致。 图8 Uao′、Ubo′相电压波形Fig.8 Uao′ and Ubo′ phase voltage waveform 图9 减速反向过程Uab线电压波形Fig.9 Reverse the process of deceleration Uab line voltage waveform 图10 A相电流波形Fig.10 A phase current waveform 为测试在非脆弱鲁棒控制时系统对参考信号的跟随性能,在实验中,速度参考值遇到限位开关时反向,电动机的速度能够较好地跟随输入变化。系统为数字控制系统,采用直线光栅尺测速,速度是经过DSP计算后在虚拟示波器上进行显示的,其计算过程需要采用标幺值。当速度的标幺值调整为0.08时,对应的速度为42.24 mm/s,采用虚拟示波器测量的v波形如图11所示,对应的q轴电流波形如图12所示。图中,进给系统具有对参考信号的快速跟随作用,而波形波动明显,主要是因为动子处于悬浮状态所引起。通过以上的实验研究,对该电动机非脆弱鲁棒控制的可行性进行了实际验证。 图11 速度波形Fig.11 Velocity waveforms 图12 q轴电流波形Fig.12 Iq current waveforms 5结论 1)针对磁悬浮永磁直线电动机的特殊运行方式,特别是要运行在不同的悬浮高度,存在参数摄动突出的问题,建立了包含磁悬浮永磁直线电动机参数摄动和不确定性扰动的数学模型,进而得到描述系统鲁棒控制的状态空间模型。 2)根据H∞性能指标与Riccati不等式的等价性,推导出参数不确定性的磁悬浮永磁直线电动机控制系统的非脆弱鲁棒H∞控制器的解析表达式。 3)在Matlab下,对非脆弱鲁棒H∞控制的磁悬浮永磁直线电动机系统进行了仿真研究,该控制器能够有效抑制电动机参数变化、控制器参数摄动及外部扰动对控制系统的影响。 4)对磁悬浮永磁直线电动机控制系统进行了部分实验研究。测量了系统的相电压和线电压,空载起动时相电流以及速度波形,与理论分析结果基本一致。通过实验对该电动机磁悬浮运行的可行性进行了实际验证,为进一步深入研究提供了科学依据。 参考文献 [1]张鲁,寇宝泉,赵斌超,等.新型Halbach次级结构永磁同步直线电机[J].电工技术学报,2013,28(7):39-45. Zhang Lu,Kou Baoquan,Zhao Binchao,et al.A novel synchronous permanent magnet linear motor with halbach secondary structure[J].Transactions of China Electrotechnical Society,2013,28(7):39-45. [2]陆华才,江明,郭兴众,等.永磁直线同步电机推力波动约束[J].电工技术学报,2012,27(3):128-132. Lu Huacai,Jiang Ming,Guo Xingzhong,et al.Thrust ripple suppression for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society,2012,27(3):128-132. [3]刘成颖,王昊,张之敬,等.基于非线性电感分析的永磁直线同步电机电磁推力特性研究[J].中国电机工程学报,2011,31(30):69-76. Liu Chengying,Wang Hao,Zhang Zhijing,et al.Research on thrust characteristics in permanent magnet linear synchronous motor based on analysis of nonlinear inductance[J].Proceedings of the CSEE,2011,31(30):69-76. [4]王昊,张之敬,刘成颖.永磁直线同步电机纵向端部效应补偿方法[J].中国电机工程学报,2010,30(36):46-52.Wang Hao,Zhang Zhijing,Liu Chengying.Compensation methods of longitudinal end in permanent-magnet linear synchronous motor[J].Proceedings of the CSEE,2010,30(36):46-52. [5]闫光亚,艾武,陈冰,等.永磁直线同步电机ADRC控制系统[J].电工技术学报,2011,26(9):60-66. Yan Guangya,Ai Wu,Chen Bing,et al.PMLSM active disturbance rejection control[J].Transactions of China Electrotechnical Society,2011,26(9):60-66. [6]陈一秀,王永初.直线伺服系统的鲁棒保性能控制研究[J].中国电机工程学报,2006,26(24):174-178.Chen Yixiu,Wang Yongchu.Study on robust guaranteed cost control for linear motor servo system[J].Proceedings of the CSEE,2006,26(24):174-178. [7]申铁龙.H∞控制理论及应用[M].北京:清华大学出版社,1996. [8]蓝益鹏,刘宇菲.磁悬浮直线电动机H∞鲁棒控制器及其蚁群算法优化设计[J].控制理论与应用,2015,32(4):527-532 Lan Yipeng,Liu Yufei.Maglev linear motor H∞ robust controller design optimization and ant colony optimization algorithm design[J].Control theory and Applications,2015,32(4):527-532. [9]Peterson I R,McFarlane D C.Optimal guaranteed cost control of uncertain linear systems[C]//America Control Conference,Chicago,IL:2929-2930. [10]Li S H,Zhou M M,Yu X H.Design and implementation of sliding mode control method for PMSM speed regulation system[J].IEEE Transactions on Industrial Informatics,2013,4(9):1879-1891. 蓝益鹏男,1962年生,副教授,博士,博士生导师,研究方向为电机及其控制、鲁棒控制。 E-mail:lanyipengg@163.com(通信作者) 陈其林男,1990年生,硕士研究生,研究方向为直线电机伺服系统。 E-mail:1172732825@qq.com Research on Non-Fragile Robust Control for Magnetic Levitation Permanent Magnet Linear Motor Control System LanYipengChenQilinHuXuechengLiuYufei (School of Electrical EngineeringShenyang University of TechnologyShenyang110870China) AbstractIn the magnetic levitation permanent magnet linear motor control system, there are the problems of parameter variation, disturbance uncertainties, and parameter perturbation in controller. Therefore, in order to realize the precise control for the levitation permanent magnet linear motor drive system of computerized numerical control machine tools, the non-fragile robust control is proposed. The state-space model considering magnetic levitation permanent magnet linear motor parameters perturbation and external disturbances is firstly set up. Then, based on Riccati inequality, the analytic expressions of the H∞ controller are derived to meet the non-fragile robust performance. The simulation research is carried out with the Matlab software. Simulation results show that the magnetic levitation permanent magnet linear motor control system has robustness for the parameter and disturbance uncertainties as well as the controller parameter perturbation. The results of the experimental prove the effectiveness of the control method. Keywords:Magnetic levitation,permanent magnet linear motor,control system,non-fragile robust control 作者简介 中图分类号:TM 383 收稿日期2015-09-10改稿日期2015-12-02 国家自然科学基金资助项目(50975181)。