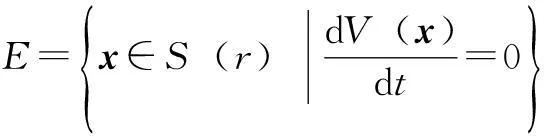基于输入观测器理论的电流谐波检测方法
李 钷 张怡茹
(厦门大学航空航天学院 厦门 361005)
基于输入观测器理论的电流谐波检测方法
李钷张怡茹
(厦门大学航空航天学院厦门361005)
摘要基于输入观测器理论,对电流谐波在线检测问题进行了研究,得到了一种能够快速准确地提取电流信号中各频率分量的方法。首先,将被测电流信号和其各频率的分量作为状态量,构建线性时变的状态空间模型。然后,设计基于状态空间模型的观测器对未知状态变量进行在线观测,从而实现各频率分量的信息提取。所设计的观测器是时变的,其稳定性和收敛性由Lyapunov定理及Lasalle不变集原理所证明。最后,搭建仿真和实验平台对该方法进行验证,结果表明其具备检测速度快、精度高、动态跟踪性能和抗干扰性好等优点。
关键词:谐波检测输入观测器状态空间模型稳定性分析
0引言
由于非线性负载(如整流器、变频器等)被大量使用,给电网带来大量的谐波污染。谐波污染不仅会造成各级电网和各种用电设备的损耗,还会引发各级保护误动等问题[1]。根据IEEE 519—1922标准规定工业中总谐波失真率不能超过5%。电力系统中谐波分量的快速、准确检测对电能质量的治理和谐波抑制与补偿具有十分重要的意义[2]。
针对谐波检测问题,特别是基波检测,国内外学者进行了大量研究,提出了很多方法。传统的方法及其改进算法可分为频域和时域两部分。频域谐波检测方法主要包括基于傅里叶分析的FFT检测法[3,4]、基于小波变换的检测方法[5]和滤波器法[6,7]。时域谐波检测方法主要包括基于瞬时无功功率理论检测方法[8,9]、基于Ip-Iq的检测方法[10,11]。另外,还有很多智能检测算法,如神经网络自适应预测算法[12]、BP神经网络[13]、自适应基波提取方法[14]、变步长的自适应检测[15]等。文献[16]对以上各种方法的固有特性及适应范围进行了细致的比较研究。
除了以上方式外,一些新的方法和思想被引入谐波检测。如基于经验模态分解理论的谐波检测方法[17]、共轭-旋转矢量不变性技术[18]及观测器方法[19]等。经验模态分解理论的方法首先构造当前时刻采样值始终处于中心位置的向量,然后计算总体谐波分量的在线检测。共轭-旋转矢量不变性技术的检测方法利用旋转因子共轭矩阵代替旋转因子做阵列信号处理,采用总体最小二乘法减小噪声信号的影响,从而准确提取出谐波参数。观测器方法针对周期信号的提取设计了一种迭代的观测器。依据该原理,文献[20]设计了一种算法,用于电力配电网中谐波的估算,这种迭代观测器能够观测被测信号的幅值和相位大小[20]。
以上方法均以单次谐波提取为目的进行研究,采用并联的方法,也可同时用于多次谐波的提取[21,22]。同时对多次谐波进行提取,一方面有利于电网的保护与谐波源分析,另一方面有利于选择性谐波消除[23,24]。针对该问题,文献[25,26]设计了线性龙贝格观测器进行谐波在线提取,并研究了观测器针对时变的不同频率谐波下的准确性和鲁棒性,但文献[26]是对各次谐波的瞬时值进行观测,若要得到电网谐波的幅值和相位信息,还需要进一步计算。文献[27]针对周期输入的线性系统,提出构建一个观测器来估计未知周期性输入量,对观测器渐进收敛性进行了分析,并对该方法进行了理论的总结和证明,将输入信号写成傅里叶级数形式,对周期线性系统的未知输入重构并计算,设计一个时变的观测器来估计输入信号,通过一个典型的Lyapunov函数,并结合Cauchy series和Parseval equality等理论证明了观测器的收敛性。
本文基于输入观测器理论,提出了一种在线电流谐波检测方法,能够精确快速地检测出信号中各频率分量。未知的电流信号可分解为有限傅里叶级数的形式,将被测电流引入一个动态的积分环节,将该信号和各频率的分量作为新的状态量,构建了时变的状态空间模型。基于该模型构造时变的观测器,准确地观测出电流中未知状态量。观测器详细的稳定性和收敛性分析由Lyapunov定理及Lasalle不变集原理所论证。
1观测器方法谐波检测原理
1.1问题描述
令im(t)为待测周期性电流信号,由于im(t)可看做是由直流、基波和前n次谐波分量之和组成,则将其表示为傅里叶级数的形式
(1)
式中,ω为角频率,ω=2πf,f=50 Hz;a0为直流分量;aicos(iωt)+bisin(iωt)为频率iω(i=1,2,…,n)的正弦信号。
第i次分量的幅值和初始相位分别为
(2)
(3)
如果观测出参数{a0,a1,b1,…,ai,bi,…,an,bn}的值,代入式(2)和式(3),就可以计算出各频率分量的幅值和相位,即实现了对电流信号im的直流量、基波和谐波的检测。
将im作为输入量,通过一个积分环节构造一个动态系统,该系统的一阶状态空间方程描述为
(4)
在稳态工作的情况下,谐波系数{a0,a1,b1,…,an,bn}是缓慢变化的。为了观测各频率分量系数ai和bi的值,将各频率分量作为新的状态量,即
(5)
式(5)的状态空间方程拓展为增广矩阵的形式为
(6)

(7)
式(6)所描述的模型是线性时变系统。
1.2观测器设计
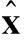
(8)
式中,误差信号的加权矩阵L(ωt)为一个(2n+2)×1的矩阵
L(ωt)=[l0la0la1cos(ωt)lb1sin(ωt)
…lancos(nωt)lbnsin(nωt)]T
(9)
式中,l0、la0、la1、 …、lan、lbn均为常数。

图1 观测器状态估计的闭环模型Fig.1 Closed loop model for observer state estimation
1.3观测器有效性证明

(10)
证明1:由于D是一个正定对角阵,那么
(11)
式中,V为连续可微且满足

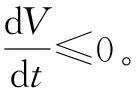
故V为Lyapunov函数,命题1得证。
证明2:由于误差系统是时变系统,采用Lasalle不变集原理证明观测器的有效性如下:
定义集合S(r)={x∈R2(n+1)|V(x) (12) (13) 由于集合{1cos(ωt)sin(ωt)…cos(nωt)sin(nωt)}是线性无关的,故式(13)的解存在且惟一 (14) 2基于观测器的谐波检测具体实现 基于观测器的谐波检测算法的具体步骤如下: 1)采集电流信号、电网电压信号。采集被测电流信号送入积分环节,构成动态系统。采集电网电压信号,设计交流过零检测电路,检测电网电压信号的过零点如图2所示。首先令传感器采集到的电网电压信号通过比较器对应一个周期的电网电压,输出占空比为50%的方波,输入到控制芯片,捕捉到方波的上升沿来确定该周期的角频率及消除相位累计误差。 图2 过零检测示意图Fig.2 Zero crossing detection scheme 3)由观测器方程(8)可知 (15) (16) 电网中电流的频率是在变化的,为了保证算法中的频率信息和被测电流的频率一致,需要对式(16)中相位θ(k)做如下迭代计算,如图3所示。首先,由于频率是缓慢变化的,故可使用上一个工频周期末计算得到的角频率用在本周期,进行相位的累加,使算法内部的频率与被测信号的频率近似相等。但由于误差存在是不可避免的,在相位累加的过程中会造成误差的累积,为了避免这种情况的发生,在每个检测到的上升沿,清零θ来消除累积误差,也就在每个工频周期末清零了相位误差。 图3 θ(k)的迭代计算Fig.3 Iterative computation of θ(k) 3谐波检测法特性分析 对大量的电网谐波频谱分析可知,谐波分量主要集中在较低次的频率上。本文对被测电流中5、7、11、13频次的谐波进行了仿真和实验分析。 3.1仿真数据验证 为了验证观测器算法检测谐波的效果,利用Matlab/Simulink仿真软件对算法的特性进行仿真研究。整流电路是常见的谐波源,如图4所示。仿真采用A相电流作为检测对象,使用电流传感器采集电流信号进入调理电路,使用电压传感器采集相间电压送入过零检测电路得到频率信息,这两部分信号作为输入进行谐波检测。 图4 在Simulink中搭建的三相不控整流仿真模型Fig.4 The Simulation model of three phase uncontrolled rectifier in Simulink 仿真模型的参数见表1。 表1 仿真模型参数 3.1.1跟踪误差分析 图5a为对仿真电流和观测电流的误差分析,其中误差电流为仿真电流和观测电流的差值。需要说明的是,这里的“仿真电流”是指Simulink模型进行仿真运算时电网侧的电流,即需要进行谐波检测的电流;这里的“观测电流”(包括后文图9中的观测电流)是利用本方法将基波、3、5、7、9、11、13次谐波检测出来以后相加,重构出来的电流(在对称三相交流电路中不存在3次及倍频谐波),因为是由观测器检测出来的,所以简称为“观测电流”。误差电流是仿真电流和观测电流的差值。可以看出,在短暂的振荡后,观测电流能迅速跟踪上仿真电流。误差电流的变化范围在±0.1 A之内。 图5b为各频次谐波分量的参数{a0a1b1…anbn}的收敛过程。从图中可以看出,参数能够在观测电流一个周期内收敛。 图5 观测器动态特性(t=0 s)Fig.5 The observer’s dynamic characteristics (t=0 s) 3.1.2加入噪声的情况下负载变动时的动态特性 为了研究本方法的抗干扰能力,在被测电流信号中加入白噪声。其中,白噪声的方差为0.01 A。同时,在仿真中模拟负载发生突变的情况,在0.15 s时,当负载电阻从5 Ω变化到10 Ω,被测电流幅值减小一半。观察算法跟踪能力,仿真结果如图6和图7所示。 图6 负载突变时(t=0.15 s)观测器动态特性Fig.6 The observer’s dynamic characteristics when the load changes at t=0.15 s 图7 检测的基波、5、7和总谐波电流波形图Fig.7 Detection of the fundamental,5,7 and the total harmonic wave 图6为观测器的各频次谐波分量参数{a0a1b1…anbn}的收敛过程。从图6中可看出,噪声对参数的收敛并无影响,能够在一个工频周期内归于稳定。在0.15 s负载发生突变时,{a0a1b1…anbn}能够迅速收敛到新的值。 从图7中可看出,基于观测器的谐波检测方法克服了瞬时无功功率等检测方法只能测出总谐波电流的局限性,可以同时检测出各指定频次的谐波分量。由于仿真采用的是三相对称电路,故而电流谐波不含偶次项,而且3倍数谐波的值也很小。在0.15 s负载发生突变时,检测的各频率的电流也能够平稳地过渡到新的状态。 从图6和图7可以看出,在被测电流中加入白噪声的情况下,观测器能迅速检测出各频率的电流,说明该方法具有很好的抗干扰能力。在负载突然变化的情况下,检测出的基波和谐波电流逐渐变化,没有出现明显过冲,具有很好的动态跟踪特性。能够在一个电网周期内快速地跟踪基波,延时非常小,约为0.01 s,具有很好的实时性。而神经网络自适应预测算法和Ip-Iq算法在解决类似问题时,进行谐波检测的响应速度为0.015 s以及0.025 s[12],说明观测器方法在负载电流发生变化时,具有快速的响应能力。 3.1.3准确性分析 为了验证该方法对各频次谐波值检测的准确性,将本文检测方法与FFT算法进行对比分析,见表2,其中ai和bi是取稳定后的平均值。由表2可见,与FFT算法得出的谐波分量对比,本方法的相对误差小于0.8%,表明观测器算法能准确检测出电流中的基波和谐波分量。 3.2实验数据验证 本文搭建了一个负载为三相不控整流器的实验平台,如图8所示。实验条件:采用调压器调压,使三相不控整流器输入端线电压有效值为10 V,电压源频率为50 Hz。实验参数:电感L1、L2、L3均为6 mH, 表2 FFT方法与观测器方法对比(仿真) 负载电阻为500 W/5 Ω的电阻,采用MDS60-16DACO三相不控整流桥,HAS 50-S/SP50 LEM电流传感器,采用NI CompactRIO-9073设备对信号进行采样和计算,频率为20 kHz。 图8 实验平台Fig.8 The experimental platform 利用FFT算法和观测器方法对实验负载电流的检测结果进行对比分析,如表3所示,各次谐波分量的相对误差小于1.5%。需要说明的是,FFT分析结果是利用NI的CompactRIO对实验的网侧电流进行采集,然后导入Matlab/Simulink的FFT Analysis模块分析得到的。 表3 FFT方法与观测器方法对比(实验) 在0.3 s时,设置负载R发生突变,电阻值从5 Ω突变到10 Ω,实验负载电流也发生相应突变。从图9中可看出,当被测电流发生突变时,观测的各频次谐波分量的值也能迅速收敛,稳定到新的值,体现了较好的鲁棒性。 图9 负载突变时(t=0.3 s)观测器动态特性Fig.9 The observer’s dynamic characteristics when the load changes at t=0.3 s 4结论 本文提出了一种基于输入观测器理论的电流谐波检测方法。该方法令被测电流经过一个积分环节,构成一个状态量,并将基波和各次谐波分量作为新的状态量,设计观测器对其进行观测,并利用Lyapunov定理和Lasalle不变集原理对观测器进行了收敛性和稳定性分析。 本文是在传统的基波提取方法的应用领域的一种扩展,不受电路拓扑的影响,不仅可用于三相对称电路,还能用于单相以及不对称电路的电流谐波提取;与传统瞬时无功功率相比,不仅可检测总谐波电流,而且可测量基波和各频次谐波分量;与FFT方法相比较,能够精确地检测出谐波;与神经网络自适应预测算法以及Ip-Iq算法相比,当负载电流发生突变时,本方法谐波参数的收敛速度更快,具备很好的动态跟踪性;另外本方法对噪声具有很好的抗干扰性。仿真和实验结果论证了以上特性。研究如何将本方法应用到APF中的谐波检测环节以生成全数字的APF控制器是未来的研究方向。 参考文献 [1]Barros J,Diego R I,De Apraz M.A discussion of new requirements for measurement of harmonic distortion in modern power supply systems[J].IEEE Transactions on Instrumentation and Measurement,2013,62(8):2129-2139. [2]熊杰锋,李群,袁晓冬,等.电力系统谐波和间谐波检测方法综述[J].电力系统自动化,2013,37(11):125-133.Xiong Jiefeng,Li Qun,Yuan Xiaodong,et al.Detection methods of harmonics and inter-harmonics in power systems[J].Automation of Eletric Power Systems,2013,37(11):125-133. [3]许珉,刘玮.加8项余弦窗插值FFT算法[J].电力系统保护与控制,2015,43(11):27-32. Xu Min,Liu Wei.An interpolation FFT algorithm based on 8-term cosine window[J].Power System Protection and Control,2015,43(11):27-32. [4]曾博,唐求,卿柏元,等.基于Nuttall自卷积窗的改进FFT谱分析方法[J].电工技术学报,2014,29(7):59-65. Zeng Bo,Tang Qiu,Qing Baiyuan,et al.Spectral analysis method based on improved FFT by nuttall self-convolution window[J].Transactions of China Electrotechnical Society,2014,29(7):59-65. [5]李正明,徐敏,潘天红,等.基于小波变换和HHT的分布式并网系统谐波检测方法[J].电力系统保护与控制,2014,42(4):34-39. Li Zhengming,Xu Min,Pan Tianhong,et al.A harmonic detection method for distributed connected grid system by using wavelet transform and HHT[J].Power System Protection and Control,2014,42(4):34-39. [6]于静文,薛蕙,温渤婴.基于卡尔曼滤波的电能质量分析方法综述[J].电网技术,2010,34(2):97-103. Yu Jingwen,Xue Hui,Wen Boying.A survey on Kalman filtering based methods for power quality analysis[J].Power System Technology,2010,34(2):97-103. [7]周雪松,周永兵,马幼捷.基于自适应滤波器的电网谐波检测[J].电网技术,2008,32(16):91-95. Zhou Xuesong,Zhou Yongbing,Ma Youjie.A power harmonic detection method based on adaptive filter[J].Power System Technology,2008,32(16):91-95. [8]罗超,陶顺,肖湘宁,等 瞬时无功功率理论与电流物理分量理论的比较与分析[J].电力系统自动化,2013,37(23):130-135. Luo Chao,Tao Shun,Xiao Xiangning,et al.Comparison and analysis of instantaneous reactive power theory and currents’ physical compoments theory[J].Automation of Electric Power System,2013,37(23):130-135. [9]何英杰,邹云屏,黄柱,等.基于瞬时无功功率理论的改进谐波检测算法[J].电网技术,2007,31(6):79-83. He Yingjie,Zou Yunping,Huang Zhu,et al.An improved algorithm for harmonic current detection based on instantaneous reactive power theory[J].Power System Technology,2007,31(6):79-83. [10]孟珺遐,周子冠,李光辉,等.基于ip-iq方法的畸变电流检测及其实现[J].电网技术,2012,36(5):125-131. Meng Junxia,Zhou Ziguan,Li Guanghui,et al.Detection of distorted current based on ip-iq method and its physical realization[J].Power System Technology,2012,36(5):125-131. [11]王存平,尹项根,熊卿,等.一种改进的ip-iq无功电流检测方法及其应用[J].电力系统保护与控制,2012,40(13):121-126. Wang Cunping,Yin Xianggen,Xiong Qing,et al.An improved ip-iq reactive current detecting method and its application[J].Power System Protection and Control,2012,40(13):121-126. [12]陈淑华,付青,马桂龙,等.基于神经网络自适应预测算法的谐波检测[J].电工技术学报,2011,26(增1):201-207. Chen Shuhua,Fu Qing,Ma Guilong,et al.Harmonic detection based on artificial neural network and adaptive predictive algorithm[J].Transactions of China Electrotechnical Society,2011,26(S1):201-207. [13]王凯亮,曾江,王克英.一种基于BP神经网络的谐波检测方案[J].电力系统保护与控制,2013,41(17):44-48. Wang Kailiang,Zeng Jiang,Wang Keying.A harmonic detecting scheme based on BP neural network[J].Power System Protection and Control,2013,41(17):44-48. [14]张斌,张东来.电力系统自适应基波提取与频率跟踪算法[J].中国电机工程学报,2011,31(25):81-89. Zhang Bin,Zhang Donglai.Adaptive fundamental component extraction and frequency tracking algorithm for power systems[J].Proceedings of the CSEE,2011,31(25):81-89. [15]刘传林,刘开培.基于新型变步长算法的自适应三相电路谐波检测[J].电力系统保护与控制,2013,41(7):123-128. Liu Chuanlin,Liu Kaipei.Adaptive harmonic detection of 3-phase circuits based on a novel variable step-size algorithm[J].Power System Protection and Control,2013,41(7):123-128. [17]朱宁辉,白晓民,董伟杰.基于EEMD的谐波检测方法[J].中国电机工程学报,2013,33(7):92-98,14. Zhu Ninghui,Bai Xiaomin,Dong Weijie.Harmonic detection method based on EEMD[J].Proceedings of the CSEE,2013,33(7):92-98,14. [18]程志友,程晨,付学敏,等.基于共轭-旋转矢量不变性技术的谐波检测方法[J].电工技术学报,2013,28(5):274-279. Cheng Zhiyou,Cheng Chen,Fu Xuemin,et al.Harmonic detection method based on conjugate signal parameters via rotational invariance techniques[J].Transactions of China Electrotechnical Society,2013,28(5):274-279. [19]Friedland B.Control System Design:An Introduction to State-Space Methods[M].New York:McGraw-Hill Inc,1987. [20]Dash P K,Swain D P,Liew A C,et al.An adaptive linear combiner for on-line tracking of power system harmonics[J].IEEE Transactions on Power Systems,1996,11(4):1730-1735. [21]Carlos A G J,Perez E,Arino C,et al.Optimization algorithm for selective compensation in a shunt active power filter[J].IEEE Transactions on Industrial Electronics,2015,62(6):3351-3361. [22]吕自波,李楚杉,邓焰,等.一种适用于新型直接交交型有源滤波器的逐次分序谐波检测算法[J].中国电机工程学报,2015,35(6):1473-1481. Lü Zibo,Li Chushan,Deng Yan,et al.A harmonic detection method by separated sequence and order suitable for novel direct AC-AC based active power filters[J].Proceedings of the CSEE,2015,35(6):1473-1481. [23]曹武,江楠,刘康礼,等.改进谐波分次检测结合集中电流环的APF谐波独立控制实现[J].中国电机工程学报,2014,34(3):387-396. Cao Wu,Jiang Nan,Liu Kangli,et al.An improved control structure consisting of selective harmonic detection and centralized current loop for the independent harmonic control and implementation of APF[J].Proceedings of the CSEE,2014,34(3):387-396. [24]周明磊,游小杰,王琛琛,等.特定次谐波消除调制方式的谐波特性分析[J].电工技术学报,2013,28(9):11-20. Zhou Minglei,You Xiaojie,Wang Chenchen,et al,Harmonic analysis of selected harmonic elimination pulse width modulation[J].Transactions of China Electrotechnical Society,2013,28(9):11-20. [25]Selvajyothi K,Janakiraman P A.Analysis and simulation of single phase composite observer for harmonics extraction[C]//PEDES’06 International Conference on Power Electronics,Drives and Energy Systems,New Delhi,India,2006:1-6. [26]Selvajyothi K,Janakiraman P A.Extraction of harmonics using composite observers[J].IEEE Transactions on Power Delivery,2008,23(1):31-40. [27]Chauvin J,Petit N.Periodic inputs reconstruction of partially measured linear periodic systems[J].Automatica,2012,48(7):1467-1472. 李钷男,1982年生,博士,助理教授,研究方向为电力电子建模与控制。 E-mail:lipo@xmu.edu.cn 张怡茹女,1991年生,硕士研究生,研究方向为谐波检测理论及方法。 E-mail:zyrxmu@foxmail.com(通信作者) A Current Harmonics Detection Method Based on Input Observer Theory LiPoZhangYiru (School of Aerospace EngineeringXiamen UniversityXiamen361005China) AbstractBased on the input observer theory, the online current harmonics detection method is proposed, which can detect all the frequency components within the current signal accurately and rapidly. Firstly, by setting the state variables as the value and each frequency component of the measured current, a linear time-varying state space model is established. Then, based on the proposed model, a time-varying observer is constructed to estimate the unknown states in order to achieve the extraction of each frequency component. The stability and convergence of the observer are proved by the Lyapunov theorem and the Lasalle invariant set principle. Finally, the simulation and experimental results show that the proposed method has advantages in detection speed, accuracy, dynamic tracking performance, and robustness. Keywords:Harmonic detection, input observer, state space model, stability analysis 作者简介 中图分类号:TM935 收稿日期2015-06-10改稿日期2015-09-18 中央高校基本科研业务费资助项目(20720150088)。