基于ADAMS的工业机器人轨迹精度模型研究
费家人,朱坚民,黄春燕
(上海理工大学 机械工程学院,上海 200093)
基于ADAMS的工业机器人轨迹精度模型研究
费家人,朱坚民,黄春燕
(上海理工大学 机械工程学院,上海200093)
摘要预测工业机器人轨迹精度对高精度加工具有重要影响,分析影响其轨迹精度的因素,基于ADAMS提出一种考虑结构参数误差及关节转角偏差的轨迹精度模型。应用激光跟踪仪辨识工业机器人结构参数与名义值间存在的偏差,分析关节转角偏差随工况的变化,在ADAMS环境下建立轨迹精度模型。以UR5机器人为实验对象,API激光跟踪仪为测量仪器对其轨迹精度进行测量,与模型输出结果进行对比,实验结果表明,该模型可准确预测工业机器人轨迹精度,预测精度可达0.5 mm,且参考该预测结果进行误差补偿后,轨迹精度基本达到1 mm以内。
关键词工业机器人;结构参数误差;关节转角偏差;误差预测模型
随着工业机器人在制造加工、物料搬运、高危环境等领域的广泛运用[1-2]。对于串联型工业机器人,实际与名义结构参数存在偏差以及在不同工况下负载,使关节产生转角偏差,均会影响末端执行器实到位置。
为提高工业机器人轨迹精度,目前主要通过标定工业机器人结构参数,对目标机器人进行运动学建模,通过测量有限点在局部工作区域中的空间点坐标,对比相对位置的模型坐标将其修正,最终通过算法对结构参数进行计算。工业机器人运动学建模方面,在D-H模型[3-4]基础上,文献[5~6]提出基于MD-H模型从微分运动学的角度进行参数辨识,文献[7]为分析结构参数对末端的误差影响情况,提出了考虑位置和角度误差的运动学模型;在参数计算方面,大部分文献利用最小二乘法[8-10]或对最小二乘法进行改进[11]计算并辨识得到机器人结构参数,另有文献[12]提出从机器人末端开始,运用递推法计算结构参数,以避免运动学参数的影响。目前的建模方法未能将影响工业机器人轨迹精度的结构尺寸、装配精度等固有属性以及关节转角偏差,直观综合地反映在参数可调的运动学模型中。ADAMS作为一种通用的多体动力学仿真软件,可用于多参数可调运动学模型的建立。本文提出了一种基于ADAMS的工业机器人轨迹精度模型建模方法,该模型可真实反映工业机器人在线情况下的物理特性参数以及关节转角偏差,解算得到含有误差的末端位置坐标,所得误差可为提高轨迹精度提供参考依据。
1基本原理
1.1轨迹精度模型建模原理
轨迹精度模型建模原理,如图1所示。驱动n自由度工业机器人单关节运动,得到n组工具中心点空间路径坐标;辨识得到结构参数即连杆尺寸L1,L2,…,Ln,关节坐标原点在Xi、Yi、Zi方向上的偏移量Δai,Δbi,Δci,以及按照右手法则关节坐标绕Xi和Yi方向上的旋转角度αi,βi;分析关节转角偏差规律,基于辨识所得结构参数建立含有结构参数误差的运动学模型,最终建立轨迹精度模型。

图1 轨迹精度模型建模原理
1.2运动学模型
导致空间轨迹误差的因素可归纳为两点:(1)机器人各部件结构参数误差,如连杆、关节的结构尺寸及装配误差,导致末端执行器执行空间轨迹时,路径所经空间位置存在误差;(2)机器人各部件运动变量误差,执行动作时各关节转角偏差累积引起的末端执行器空间位置误差。将各误差因素归纳为结构参数误差与运动输出量误差后,以D-H模型为基础,结合各项误差因素,推导得到关节i+1与关节间i的齐次变换矩阵Ai,描述含有结构参数误差与运动输出量误差的工业机器人运动学情况。
Ai=Trans(Δai,Δbi,Δci)Rot(x,αi)Rot(y,βi)Rot(z,θi)Trans(ai,bi,ci)=
(1)
式中,Ai为关节i+1坐标与关节i坐标间的变换矩阵;Δai,Δbi,Δci为关节坐标原点在Xi、Yi、Zi方向上的偏移;αi,βi为关节坐标在Xi、Yi方向上的偏转角;θi为关节i的转角值;ai,bi,ci为连杆i在Xi、Yi、Zi方向上投影的长度。

(2)
分析Qi可知转角误差引起的坐标变换误差由两部分组成:(1)固有结构尺寸、装配误差引起的Δai,Δbi,Δci与αi,βi,呈线性或常量表示;(2)运动状态下关节自身转角误差,即Qi[4,1]和Qi[4,2]呈非线性表示。根据变换矩阵理论可知,Qi[4,1]和Qi[4,2]表示在Xi、Yi方向上的移动。
1.3ADAMS多体运动学轨迹精度模型
基于上述建模原理,于ADAMS建立多体运动学轨迹精度模型,参数设置方式如表1所示。将SolidWorks世界坐标系与测量坐标系重合,建立考虑ai、bi、ci、Δai、Δbi、Δci结构参数的工业机器人三维模型。将三维模型以中性文件Parasolid(*.x_t)格式导入多体动力学仿真软件ADAMS中的ADAMS/view模块,进一步完成模型参数设置。
针对机器人各关节运动特性,对模型各部件添加相应运动副进行约束。创建Fixed Joint固定机器人基座,于旋转关节处创建Revolute Joint铰链副,通过调整设定于相邻关节部件接触面与关节旋转轴交点上Marker点,运用Precision Move-Rotate实现关节坐标偏转角的设置,其中关节坐标系的Z方向与旋转轴线重合。定义各关节铰链副以Rotational Joint Motion实现旋转运动。设定Joint Motion驱动函数为Cubspl(1st_Indep_Var,2nd_Indep_Var,Spline_Name,Deriv_Order),该函数采用Cubic Spline插值方式,无论空间点是否均布,函数导数均很准确,方程求解更易收敛。将机器人含有关节转角偏差的n组关节转角值以文本文件格式保存,导入ADAMS创建样条曲线,设定Cubspl函数中的Spline_Name变量完成驱动值设定,实现模型末端执行器输出含有误差的坐标值。
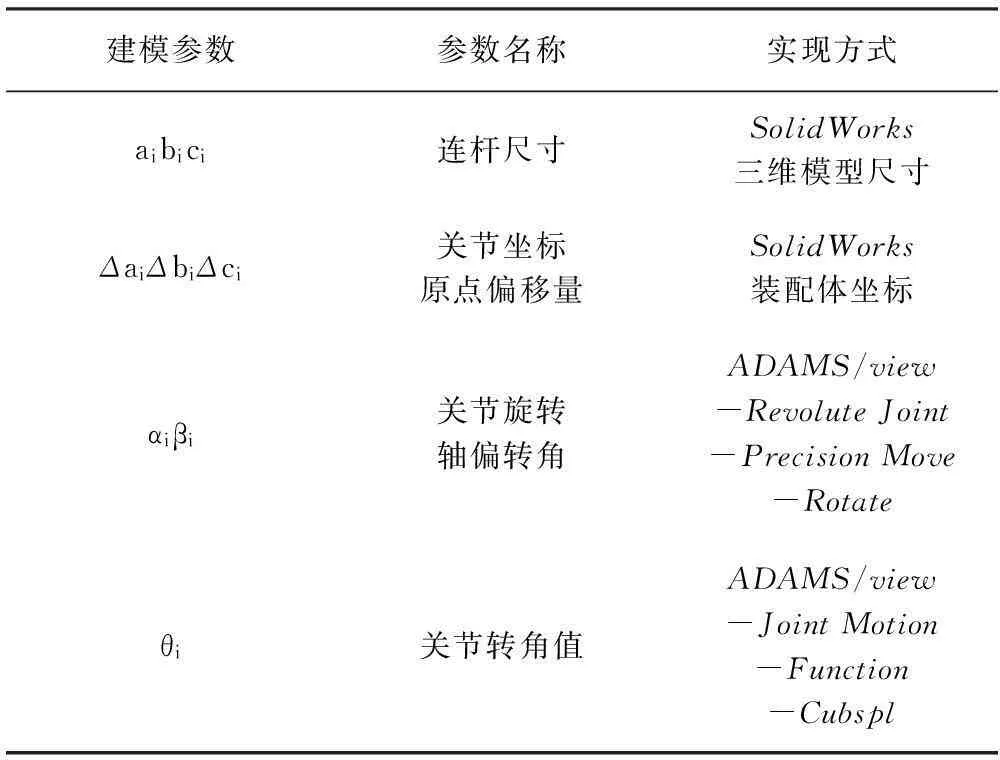
表1 模型参数实现方式
2实验方案及结果分析
2.1实验方案
以UniversalRobots公司的UR5六自由度工业机器人为实验对象,采用美国API公司生产的Tracker激光跟踪仪为测量设备。安装靶球于UR5末端执行器处,实时采集末端执行器空间位置。根据上文提出的轨迹精度模型建立方案,于ADAMS中建立模型如图2所示,包括Base、Shoulder、Elbow、Wrist1、Wrist2、Wrist3这6个部件,使用FixedJoint和RevoluteJoint两个约束条件对各部件进行约束设置。设定3条理论空间轨迹A、B、C,驱动UR5机器人运行并使用API激光跟踪仪测量工具中心点空间轨迹坐标。ADAMS仿真过程如图3所示,将考虑转角偏差值的关节驱动转角以样条曲线方式导入ADAMS,编辑模型中6个关节的JointMotion所对应的Cubspl函数,在公式编辑界面编写关节样条曲线公式,打开SimulationControl面板,设定仿真时间与步长,完成工业机器人轨迹精度模型的搭建。以实测轨迹误差为预测标准,对比ADAMS模型输出轨迹误差在X、Y、Z方向上的分布情况,验证模型准确性;根据预测所得轨迹误差分布情况,在工业机器人轨迹设定阶段进行反向补偿,得到补偿后的轨迹,分析该轨迹精度,验证轨迹精度模型有效性。
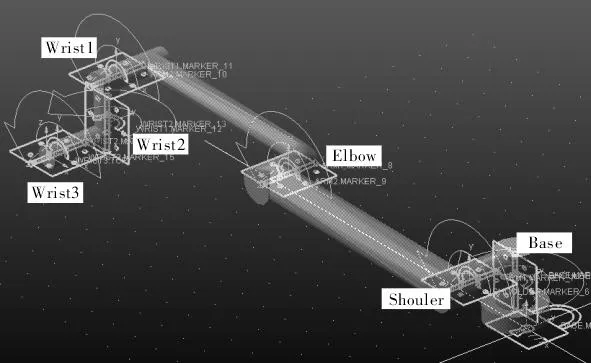
图2 ADAMS环境下工业机器人多体运动学模型
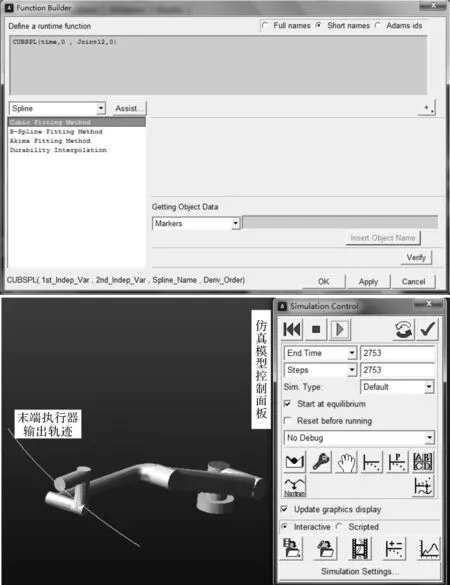
图3 工业机器人轨迹精度模型
2.2模型预测结果分析
轨迹A、B、C空间位置精度预测实验结果如图4所示,轨迹A实测误差情况为(-2.5,0.5)mm,与ADAMS模型预测得到误差(-2.5,0.5)mm一致;轨迹B实测误差情况为(-2.5,0.5)mm,与ADAMS模型预测得到误差(-2,1)mm基本接近;轨迹C实测误差情况为(-2,0)mm,与ADAMS模型预测得到误差(-2,0)mm一致。此外,对比各轨迹误差在X、Y、Z方向上的分布趋势可知,轨迹精度模型预测的误差情况与实测情况趋势相同,且分布区间相近。由此可见,基于ADAMS建立的工业机器人轨迹精度模型可有效预测工业机器人执行空间轨迹时的精度情况,且预测准确率较高。
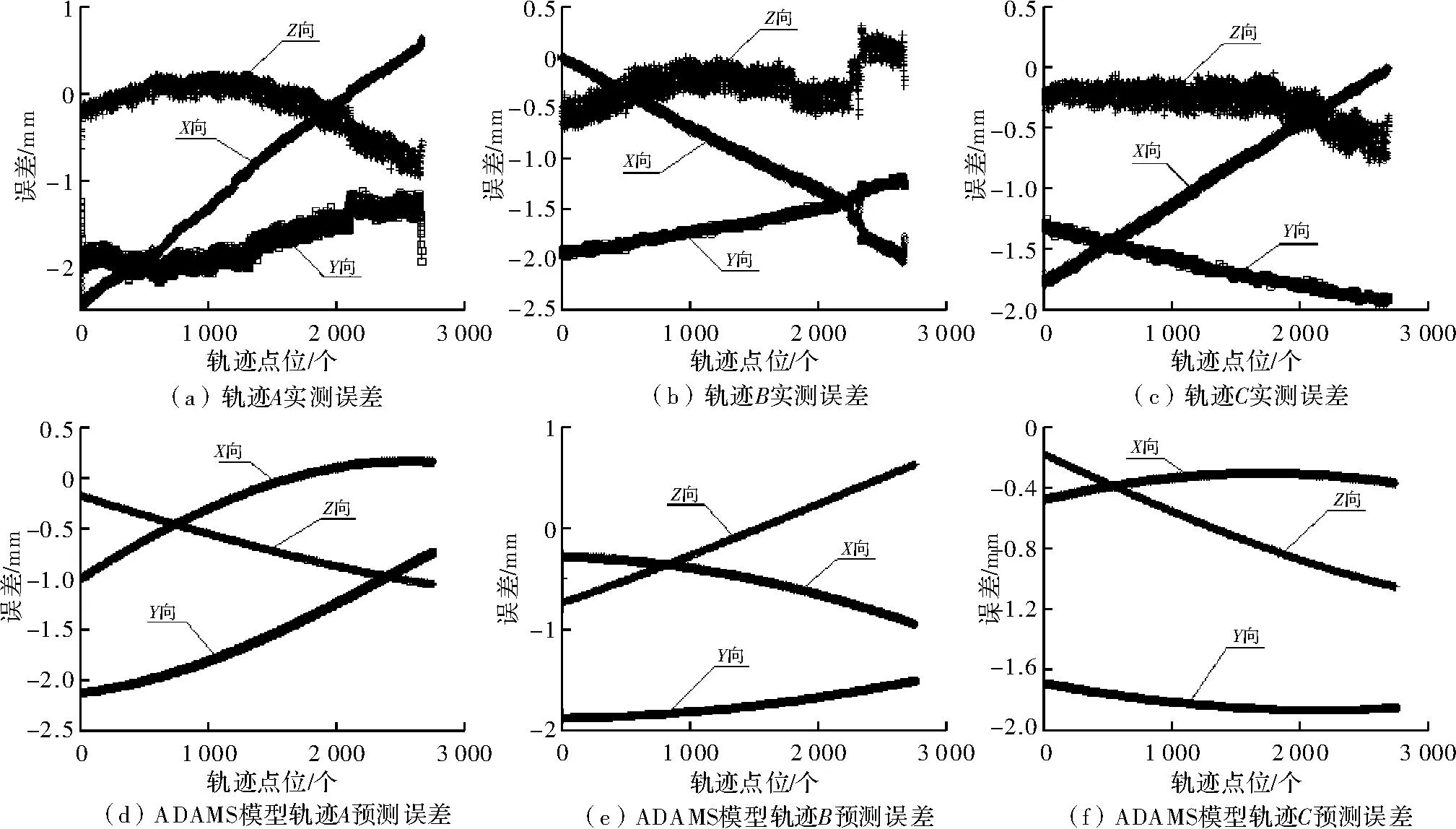
图4 A、B、C轨迹空间位置精度预测结果
2.3补偿结果分析
利用上述预测所得误差值,修正机器人驱动参数,重新测量末端轨迹空间位置坐标,得到轨迹A、B、C经补偿后的误差情况。由图5可知,补偿前A轨迹误差范围为(-2.5,0.5)mm,经补偿A轨迹精度提升至(-1.5,0.5)mm;B轨迹补偿前误差范围为(-2.5,0.5)mm,经补偿B轨迹精度提升至(-1,0.4)mm;补偿前轨迹C误差范围为(-2,0)mm,经补偿C轨迹精度提升至(-1.3,0.5)mm。由图线分析可得,X、Y、Z方向上精度提升最高达1.5mm左右,且大部分误差范围位于(-0.5,0.5)mm内,对常见工业应用领域,该精度可满足大部分作业要求,验证了轨迹精度模型的有效性。

图5 A、B、C轨迹补偿后误差情况
3结束语
(1)分析了工业机器人结构特性参数与运动特性参数对末端输出误差的影响,建立含有结构参数误差与关节转偏差的工业机器人运动学模型;(2)结合SolidWorks与ADAMS建立多体运动学仿真模型,完成六自由度工业机器人轨迹精度模型的搭建;(3)规划任意三条空间路径,运用ADAMS轨迹精度模型预测误差分布情况,通过与实测误差对比,验证预测模型准确性。运用预测所得误差情况,修正机器人驱动参数对空间位置进行补偿,结果表明补偿后空间位置精度显著提高。
参考文献
[1]王田苗,陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014,50(9):1-13.
[2]徐文福,毛志刚.核电站机器人研究现状与发展趋势[J].机器人,2011,33(6):758-767.
[3]周炜,廖文和,田威.基于空间插值的工业机器人精度补偿方法理论与试验[J].机械工程学报,2013,49(3):42-48.
[4]刘志,赵正大,谢颖,等.考虑结构变形的机器人运动学标定及补偿[J].机器人,2015,37(3):376-384.
[5]李定坤,叶声华,任永杰,等.机器人定位精度标定技术的研究[J].计量学报,2007,28(3):224-227.
[6]王一,刘常杰,任永杰,等.工业坐标测量机器人定位误差补偿技术[J].机械工程学报,2011(15):31-36.
[7]陈钢,贾庆轩,李彤,等.基于误差模型的机器人运动学参数标定方法与实验[J].机器人,2012(6):680-688.
[8]任永杰,邾继贵,杨学友,等.基于距离精度的测量机器人标定模型及算法[J].计量学报,2008,29(3):198-202.
[9]Newman W S,Brikhimer C E,Horning R J,et al.Calibration of a motoman P8 robot based on laser tracking[C].San Francisco,California:IEEE International Conference on Robotics and Automation,2000.
[10]杜亮,张铁,戴孝亮.激光跟踪仪测量距离误差的机器人运动学参数补偿[J].红外与激光工程,2015(8):2351-2357.
[11]洪鹏,田威,梅东棋,等.空间网格化的机器人变参数精度补偿技术[J].机器人,2015,37(3):327-335.
[12]陈钢,贾庆轩,李彤,等.机器人运动学参数递推标定方法[J].北京邮电大学学报,2013,36(2):28-32.
Study on the Model of Trajectory Precision for Industrial Robot Based on ADAMS
FEI Jiaren,ZHU Jianmin,HUANG Chunyan
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
AbstractThe purpose of this paper is to explore a prediction model of trajectory precision based on ADAMS,which can improve the high precision processing using industrial robots.The main factors influencing trajectory precision are the structural parameters of industrial robots and nominal value and the joint angle deviation.A structural parameters identification scheme is proposed and verified by a laser tracker and analyze the relationship of the joint angle deviation and the change of working condition.A prediction model of trajectory precision in ADAMS is built.Finally,an experiment system is established to verify the prediction model with the API III laser tracker aimed at UR5 as the measuring device.The experiment results show that the prediction model is valid with the precision of prediction close to 0.5 mm,and the trajectory precision is less than 1mm with error compensation.
Keywordsindustrial robots;error of structural parameters;joint angle deviation;error prediction model
中图分类号TP242.2
文献标识码A
文章编号1007-7820(2016)04-020-05
doi:10.16180/j.cnki.issn1007-7820.2016.04.006
作者简介:费家人(1990—),女,硕士研究生。研究方向:精密测试。朱坚民(1968—),男,博士,教授。研究方向:机电系统的智能测控。黄春燕(1990—),女,硕士研究生。研究方向:精密测试。
基金项目:国家自然科学基金资助项目(50975179)
收稿日期:2015- 11- 22

