时间分数阶延迟微分方程在流体力学中的应用

邱　宁

(青岛理工大学 琴岛学院, 山东 青岛　266106)



时间分数阶延迟微分方程在流体力学中的应用

邱宁

(青岛理工大学 琴岛学院, 山东 青岛266106)

摘要:利用一类时间分数阶微分方程描述河滩形成过程中沙子运动的模型,将传统刻画该模型的对时间一阶导数用α(0<α<1)阶导数代替,最后给出数值模拟.

关键词:时间分数阶; 延迟; 河滩; 输沙量; 数值模拟

在大河的拐弯处,由于水流的环流,弯的外侧形成凹岸,内侧形成凸岸.两岸泥沙运输率的空间差异导致凹岸和凸岸的形成演化,所以通过输沙率与时间挂钩来模拟河滩和河坎的形成演变[1].在相对理想的状态下,利用时间分数阶微分方程来描述河滩形成过程中的流沙运动过程,并给出数值模拟.

本文考虑如下河滩处泥沙输沙量的方程:

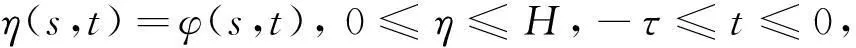
(2)

(3)

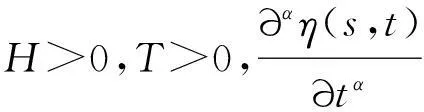
1差分格式构造

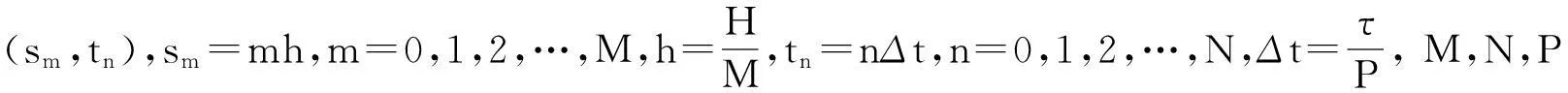
(4)

记

则式(4)整理得:

(5)

对式(2)离散后得:

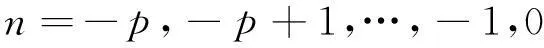
进一步整理成便于讨论的形式:

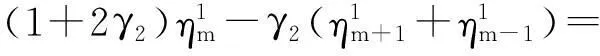
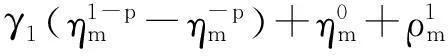
(6)

(7)

2稳定性证明

定理1差分格式(6)、式(7)无条件稳定.

证明ωk=(k+1)1-α-k1-α,所以有

由差分格式(6)、式(7)得误差方程:

(8)

(9)

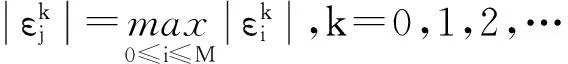
(10)

考虑到ωk满足的条件,所以上式等于

(11)

3收敛性证明

根据式(6)、式(7)和局部截断误差计算得:

(12)

(13)

定理2差分格式(6)、式(7)无条件收敛.

证明用数学归纳法.

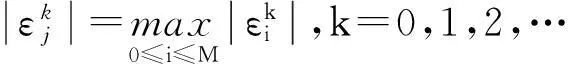
此处 C1=ταΓ(2-α)(τ+h2).

4数值算例

考虑如下问题:

算例的精确解u(x,t)=t2ex,取延迟量τ=1[5-6],令空间步长为0.1,时间步长为0.01,数值模拟结果如下.

表1　数值解的相对误差

参考文献:

[1] 杜晓琴,高抒. 水下沙丘形态演化的数值模拟实验[J]. 海洋学报, 2012,134(4):121-134.

( DU X Q, GAO S. An evolution of subaqueous dune morphology numerical experiments[J]. Acta Oceanologica Sinica, 2012,134(4):121-134.)

[2] PODLUBNY I. Fractional differential equations[M]. San Diego: Academic Press, 1999.

[3] 马亮亮. 时间分数阶扩散方程的数值解法[J]. 数学的实践与认识, 2013,43(10):248-253.

(MA L L. A numerical method for the time fractional order dispersion equation[J]. Mathematics in Practice and Theory, 2013,43(10):248-253.)

[4] 张艳敏,郭萍,段素芳. 一类时间分数阶延迟微分方程的数值解法[J]. 沈阳大学学报(自然科学版), 2014,26(4):342-344.

(ZHANG Y M,GUO P,DUAN S F. A numerical method for solving one time fractional delay differential equation[J]. Journal of Shenyang University (Natural Science), 2014,26(4):342-344.)

[5] 冯日月. 分数阶延迟微分方程数值方法的研究[D]. 哈尔滨:哈尔滨工业大学, 2009.

(FENG R Y. Numerical methods for differential equations of fractional order with time-dependent delay[D]. Harbin: Harbin Institute of Technology, 2009.)

[6] 黄典贵. 基于微可压液体的统一对流扩散型流体力学方程组[J]. 工程热物理学报, 2007(S1):153-156.

(HUANG D G. Unified convection diffusion equations based on weakly compressible liquid[J]. Journal of Engineering Thermophysics, 2007(S1):153-156.)

【责任编辑: 肖景魁】

Application of Time Fractional Delay Differential Equations in Fluid Dynamics

QiuNing

(Qindao College, Qingdao Technological University, Qingdao 266106, China)

Abstract:In this paper, by using a class of time fractional differential equations describing the motion of sand beach formation model. The time first derivative of the model is put into the model by a fractional derivative of order α(0<α<1), and numerical simulation is given in the end.

Key words:time fractional order; delay; benchland; sediment runoff; numerical simulation

中图分类号:O 241.82

文献标志码:A

文章编号:2095-5456(2016)02-0170-03

作者简介:邱宁(1980-),女,山东烟台人,青岛理工大学讲师.

基金项目:山东省高校科技计划资助项目(J15L157).

收稿日期:2015-10-29