随机约束非光滑凸优化的空间分解方法

徐　琳, 李　丹

(1. 沈阳大学 师范学院, 辽宁 沈阳　110044; 2. 沈阳市第二中学, 辽宁 沈阳　110016)



随机约束非光滑凸优化的空间分解方法

徐琳1, 李丹2

(1. 沈阳大学 师范学院, 辽宁 沈阳110044; 2. 沈阳市第二中学, 辽宁 沈阳110016)

摘要:讨论了随机约束非光滑凸优化的基于空间分解的样本均值近似(SAA)方法.在适当的条件下,SAA问题的解以概率1收敛到其真实解,并且随着样本容量的增加,收敛速度是指数的.基于分解理论,给出了求解SAA问题的超线性收敛速度的算法框架.

关键词:随机优化; 样本均值近似; 空间分解; 超线性收敛

考虑如下的随机约束非光滑凸优化

(1)

式中,f(x)=max{E[fi(x,ξ)]:i∈I=0,…,m}.对每个固定的ξ和和η,函数fi(·,ξ),i∈I和gj(·,η),j∈J是二次连续可微的凸函数.ξ和η是概率空间(Ω,γ,P)的两个随机变量,E是数学期望.

假设对任意x∈Rn,E[fi(x,ξ)],i∈I和E[gj(x,η)],j∈J有定义,令ξ1,…,ξN是ξ的样本,并且η1,…,ηN是η的样本.本文考虑基于样本的均值近似(SAA)方法,即利用fi(·,ξ)和gj(·,η)的样本均值近似它们的期望值.式(1)的SAA问题为

(2)

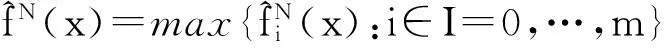
目前,SAA方法是随机优化的研究热点.文献[1]是随机优化和SAA方法的一个概述,亦可参见文献[2-6].SAA方法的基本思想是由蒙特卡罗模拟产生独立同分布的样本,并利用样本均值函数近似代替目标函数,然后利用确定型的优化方法来解决SAA问题,最后得到原问题的近似解.由于文献[1-6]中的目标函数均是光滑的,因此,其SAA问题都可由光滑牛顿法求解.

1SAA问题的收敛性分析

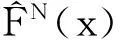
是在x处的积极指标集.

接下来讨论随着N的增大,式(2)收敛到式(1).具体地,当N→∞时,式(2)的SAA问题的解收敛到原问题的解.下面给出SAA方法的基本假设.

假设1

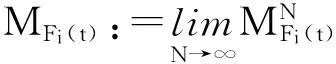
② 对任意的s∈X,矩母函数MS(t)在原点邻域内是有限值;

③ 对任意的ξ∈Ω,s′,s∈X,存在函数k:Ω→R+,使得

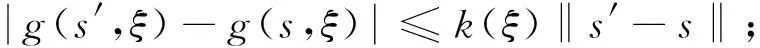
④ k(ξ)的矩母函数Mk(t)=E[etk(ξ)]在原点邻域内是有限值,其中Ms(t)=E[et(g(s,ξ)-G(s))]是随机变量g(s,ξ)-G(s)的矩母函数.

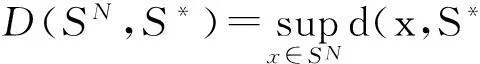
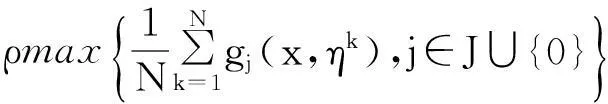
由假设1知,对于任意ε1>0,ε2>0,存在M1和M2,若N>M=max{M1,M2},则

令N>M且ε=ε1+ρε2,有

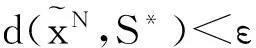
下面讨论随着样本容量的增加,式(2)的SAA问题的指数收敛率.

定理2令xN是式(2)的SAA问题的解,S*是原问题式(1)的解决.假设1成立,则对于ε>0,存在正常数c(ε)和d(ε),使得对于充分大的N,有

(3)

证明令ε>0,ε1>0,ε2>0,由定理1及

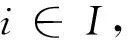
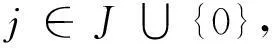
有d(xN,S)<ε.因此由假设1知

2SAA问题的分解理论

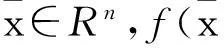
定义了VU-空间分解,并且Rn=U⊕V,其中⊕是空间的直和.

定理3假设2成立,则有如下结论:

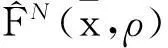
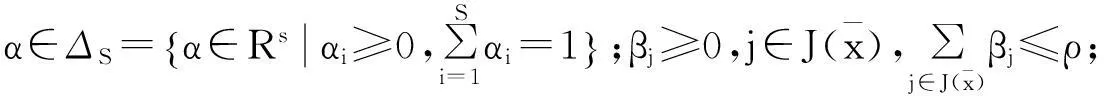
V=lin{[

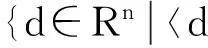
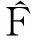
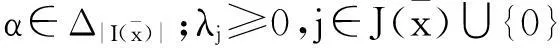
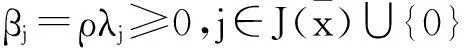
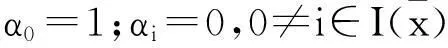
有

则由V空间的定义知

并且由U=V⊥知U空间的结构.

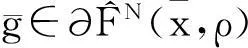
V—空间的最优解集为

定理4假设2成立,则对于充分小的u有如下结论成立:

① 非线性方程组

(4)

有唯一解v=v(u),并且v:RdimU→RdimV是二次连续可微的;

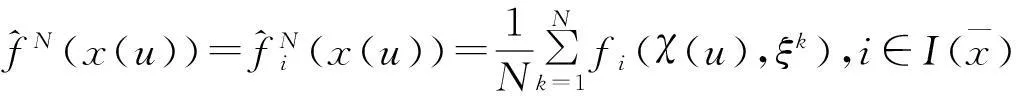
随着蔬菜价格上涨，部分菜农在经济利益的驱使下只看重眼前利益，不注重长远发展，过早采收，长期单一施用化肥农药，不断加大农药、化学肥料使用量等诸多影响蔬菜产业发展的不良现象依然存在，且有抬头之势，这些都不利于蔬菜产业的持续健康发展。一是长期偏施化肥，导致菜园土壤肥力明显下降，蔬菜抗病虫害能力减弱。二是过量施用农药、化肥，导致蔬菜中农药残毒量增高，使蔬菜中有害农药残留量和有害重金属不断增高聚积，直接影响了人们的食用安全，加重了生产者对化学农药的依赖，使喷药浓度不断加大，次数变多，造成了对环境的污染和生态系统的破坏。因此，研究天水市蔬菜农药残留现状，做好农产品质量安全监督管理工作，显得十分必要。

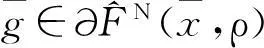
下面的定理给出了U-拉格朗日函数的一些性质.

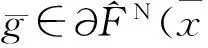
①Lu是二次连续可微函数;

②Lu的梯度为,其中

特别地,当u=0时,有

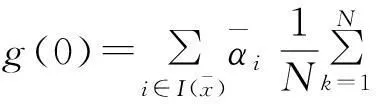
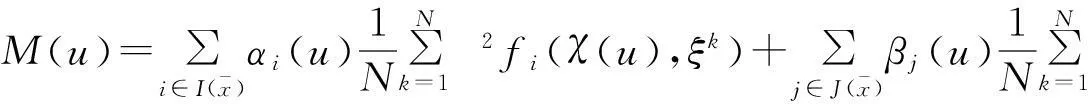
特别地,当u=0时,有

证明① 由定理4③,知

由于fi与v(u)均是二次连续可微的,知①成立.

② 根据链式法则,将下面的方程组

关于u求导,有

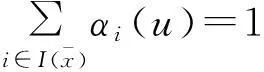
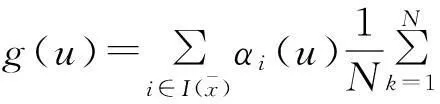
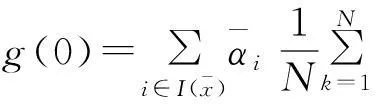
③对②关于u求导,有

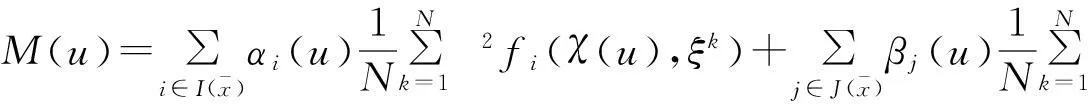
根据文献[10]中定理6.3的证明知

则有

3算法收敛性分析

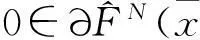
算法1

Step 1(停止准则)若

(5)

则停.

(6)

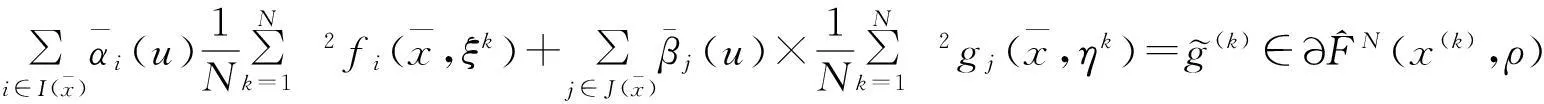
Step 6(校正)置k=k+1,转步1.

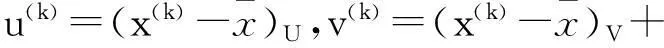
(7)

(8)

结合式(7)和式(8)有结论成立.

4结论

针对随机约束非光滑凸优化式(1),本文给出了基本空间分解理论的算法研究.该算法交替执行V-步及U-牛顿步以获得超线性的收敛速度.应用束方法的思想及迫近点落在原始轨道上的理论,算法1中的V-步可迭代求出,这也是本文的一个后续工作.

参考文献:

[1]SHAPIROA,DENTCHEVAD,RUSZCZYNSKIA.Lectureonstochasticprogramming,modellingandtheory[R].Philadelphia:SIAM, 2009.

[2] PAGNONCELLI B K, AHMED S,SHAPIRO A. Sample average approximation method for chance constrained programming: theory and application[J]. Journal of Optimization Theory and Applications, 2009,142(2):399-416.

[3] ROCKAFELLAR R T. Monotone operators and the proxiral point algorithm[J]. SIAM Journal on Control and optimization, 1976,14(5):877-898.

[4] WANG M Z, LIN G H, GAO Y L, et al. Sample average approximation method for a class of stochastic variational inequality problems[J]. Journal of Systems Science and Complexity, 2011,24(6):1143-1153.

[5] LIU Y C, ZHANG Y. Penalized sample average approximation methods for stochastic mathematical programs with complementarity constraints[J]. Mathematics of Operations Research, 2011,36(4):670-694.

[6] SHUANG C, PANG L P, GUO F F, et al. Stochastic methods based on Newton method to the stochastic variational inequality problem with constraint conditions[J]. Mathematical and Computer Modeling[J], 2012,55(3):779-784.

[7] LEMARECHAL C, OUSTRY F, SAGASTIZABAL C. The U-Lagrangian of a convex function[J]. Transactions of the American Mathematical Society, 2000,352(2):711-729.

[8] MIFLIN R, SAGASTIZABAL C. VU-decomposition derivatives for convex max-functions[M]∥Lecture Notes in Economics and Mathematical Systems. Berlin: Springer, 1999:167-186.

[9] LEMARECHAL C, SAGASTIZABAL C. More than first-order developments of convex functions: primal-dual relations[J]. Journal of Convex Analysis, 1996,3(2):1-14.

[10] MIFLIN R, SAGASTIZABAL C. On VU-theory for functions with primal-dual gradient strcture[J]. SIAM Journal on Optimization, 2000,11(2):547-571.

[11] MIFLIN R, SAGASTIZABAL C. Functions with primal-dual gradient structure and U-Hessians[M]∥Nonlinear Optimization and Related Topics. Norwell, MA: Kluwer Academic Publishers B.V, 2000:219-233.

[12] MIFLIN R, SAGASTIZABAL C. Primal-dual gradient structured functions: second-order results, links to epi-derivatives and partly smooth functions[J]. SIAM Journal on Optimization, 2003,13(4):1174-1194.

[13] LANG S. Real and function analysis[M]. 3rd ed, New York: Springer-Verlag, 1993.

[14] 张莹. 一类非光滑凸函数的超线性空间分解方法[J]. 沈阳大学学报(自然科学版), 2015,27(6):501-506.

(ZHANG Y. A superlinear space-decomposition method for a class of nonsmooth convex function[J]. Journal of Shenyang University(Natural Sciences), 2015,27(6):501-506.)

【责任编辑: 肖景魁】

A Space Decomposition Method for Stochastic Constrained Nonsmooth Convex Optimization

XuLin1,LiDan2

(1. Normal School, Shenyang University, Shenyang 110044, China; 2. Shenyang No.2 High School, Shenyang 110016, China)

Abstract:Sample average approximation (SAA) method based on space-decomposition method to solve stochastic constrained nonsmooth convex optimization is discussed. Under some moderate conditions, the SAA solution converges to its true counterpart with probability approaching one and convergence is exponential fast with the increase of sample size. Based on the decomposition theory, a superlinear convergent algorithm frame is designed to solve the SAA problem.

Key words:stochastic optimization; sample average approximation; space decomposition; superlinear convergent

中图分类号:O 221

文献标志码:A

文章编号:2095-5456(2016)02-0160-06

作者简介:徐琳(1966-),女,辽宁沈阳人,沈阳大学副教授.

基金项目:国家自然科学基金资助项目(11301347).

收稿日期:2015-10-07