轴压加固柱承载力计算理论

周　乐, 王克尧, 聂晓梅, 伊军伟, 钮　鹏

(沈阳大学 建筑工程学院, 辽宁 沈阳　110044)



轴压加固柱承载力计算理论

周乐, 王克尧, 聂晓梅, 伊军伟, 钮鹏

(沈阳大学 建筑工程学院, 辽宁 沈阳110044)

摘要:为了进一步研究轴心载荷作用下四周包裹钢筋混凝土加固钢柱的设计计算方法,分别基于我国两本规程对此加固柱的设计方法进行了分析.结果显示:持载状态下,加固柱可靠度需不大于一定初始应力水平指标;两个规范的设计遵循原有构件截面边缘屈服和加固后全截面屈服两种原则;静力载荷作用下,两规范都考虑新、旧截面应力重分布现象,动力载荷作用下只对钢材强度乘以了折减系数,且两种受力情况下都未考虑加固柱应力应变超前或滞后现象.

关键词:设计规程; 加固柱; 持载; 初始应力水平指标

四周包裹钢筋混凝土加固法是钢结构加固法中增大截面加固法的一种,当建筑不能满足继续使用功能,可用四周包裹混凝土方法进行加固,此方法不但可以保护型钢免受腐蚀,且能迅速提高钢柱的承载力.与整浇柱相比,新增钢筋和混凝土材料在第二期加载过程中的应力滞后于原型钢[1].此时若仍按新构件计算,则应对新增结构进行强度折减[2],但目前钢结构加固技术两本规范[3-4]中均未对折减系数明确标定.

持载下加固钢柱时,加固前原结构的初始缺陷、应变、后增钢筋强度利用情况等因素对加固后组合柱所能承受的极限载荷都有一定的影响[5],若忽略这些因素,会使加固柱的设计计算偏于不安全.本文对中国两个钢柱加固方面的规程[3-4],即CECS 77∶1996和YB 9257—1996中关于持载下四周包裹钢筋混凝土加固钢构件的设计方法进行分析,为进一步利用四周包裹混凝土加固钢结构方面的研究提供理论依据.

1初始应力水平指标的提出

在加固柱研究之初,引入初始应力水平指标β(钢构件加固时核心型钢应力与此型钢屈服强度比值)来保证加固柱的可靠性和安全性.β值越大,新增钢筋混凝土材料可能无法达到预期强度,β值越小,则就要求加固时尽量卸载,型钢初始载荷小,加固法的应用受限制.所以确定β值的大小,尤为重要.

我国YB 9257—1996[6-9],借鉴苏联计算方法,采用了在静载或间接承受动载时,考虑加固前后原钢柱截面应力重分布现象,而在动力载荷作用下[10],鉴于GBJ 17—1988中对承受动力载荷的结构忽略其塑性变形,计算时不考虑加固前后原钢柱截面应力重分布现象.

为提高加固后组合构件工作的可靠度,不同载荷形态的构件在加固时应有不同的应力限制值.我国YB 9257—1996在加固计算中为考虑施工条件、应力重分布等因素影响,引入了加固折减系数k,根据各类构件的不同受力条件,k的取值建议如表1.

表1　持载下折减系数k

CECS 77∶1996规定:钢结构加固方法中,增大截面法是较传统的加固方法,焊接法加固时原钢结构的实际初始持载比β应小于0.55fy(fy为钢材屈服强度或屈服点标准值),忽略新增构件的塑性变形;其他方式加固时,其实际初始应力水平指标应小于0.7fy,否则不得持载加固.

YB 9257—1996中,使用条件只分为动载和静载两种情况,是根据苏联规范进行了一定的调整,此加固方式应用范围更广;CECS 77∶1996中,针对增大截面加固法,规定相比苏联和我国另一个规范要求要严格.初始负载较小时,增大截面加固法应用受限制,初始负载过大,则原构件应变超前现象比较严重,偏于不安全,加固效果也不好.

2设计原则

YB 9257—1996规定:采用四周包裹钢筋混凝土的方法加固钢构件时,将构件全部拆卸下来放在地面上进行加固,才能彻底卸载,因此在持载状态下进行加固是不可避免的.持载状态下四周包裹钢筋混凝土加固时,从设计计算上主要有下面两个问题:①加固时,原构件中初始持载应力水平指标(σ≤βf)的取值;②加固后组合构件的计算原则,即新、旧构件之间的共同工作问题.

采用四周包裹钢筋混凝土的方法加固钢构件,完全卸载后,组合构件的强度和稳定性计算,按与普通一次性整浇柱相同的方法进行计算;持载状态下,加固后,动载作用下,加固前后原有构件的应力之和小于等于钢材的强度设计值,按原有构件截面边缘屈服的准则进行计算;承受静载或者间接承受动载的构件,考虑加固前后新、旧材料截面上的应力重分布现象,按加固后的全截面边缘屈服的原则进行承载力计算[11-13].

CECS 77∶1996中规定钢结构加固设计按一次性整浇柱的设计方法,但是考虑新、旧截面的应力重分布和原构件截面可能过多的塑性变形,按照不同的使用情况进行折减计算.

CECS 77∶1996和YB 9257—1996的设计都没有考虑新材料的应变滞后效应,CECS 77∶1996中,不分受力情况,采用加固后全截面边缘屈服准则,YB 9257—1996中,针对受力情况,采用了原构件截面边缘屈服准则和加固后全截面边缘屈服两种准则.

3设计方法

持载下加固设计,一般分为两个阶段:一是加固过程中,二是加固后.两阶段应按各阶段相应的有效截面、作用载荷和支撑条件分别进行验算;对加固后组合构件应考虑持载加固引起构件内力及自重变化等不利影响,重新予以验算.CECS 77∶1996和YB 9257—1996的计算都是按照原构件截面边缘屈服和加固后的全截面边缘屈服两个原则,并参照《钢结构设计规范》(GBJ 17)进行的.

3.1强度计算

YB 9257—1996规定:轴心受压的加固构件的强度计算规定见表2.

表2　强度计算公式

式中:N1、N分别为加固过程中一期作用下、加固后组合构件需承受的轴向载荷;f为强度最低钢材的强度设计值;A1、A2分别为原有构件的净面积、加固件的净面积.

CECS 77∶1996规定:轴心受压的加固构件的强度计算规定见表3.

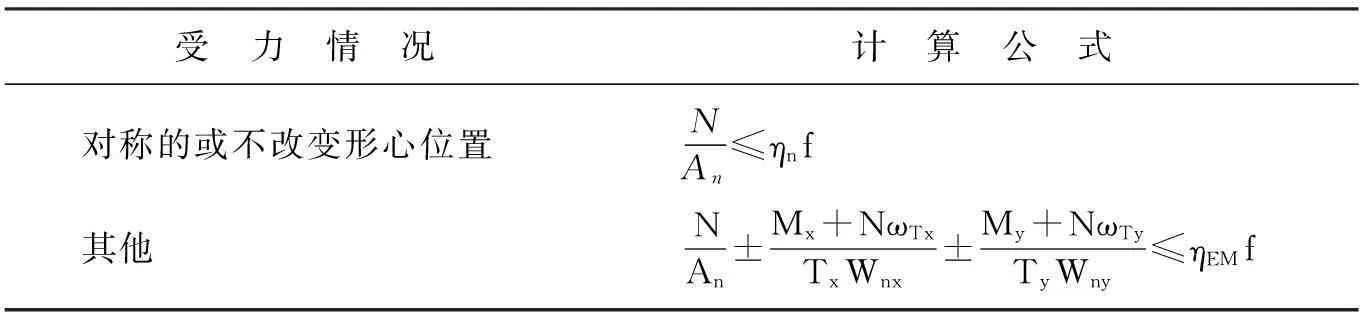
表3　强度计算公式

式中:An为加固后构件净面积;ηn为强度折减系数.对Ⅰ、Ⅱ类ηn=0.85;Ⅲ、Ⅳ类ηn=0.90;My、Mx分别为构件总轴心力绕y轴和x轴的总弯矩最大值;Wny、Wnx、ωTy、ωTx为构件对y轴和x轴的净截面抵抗矩和总挠度值,根据式(1)计算;Tx、Ty为塑性变形系数,若为Ⅰ、Ⅱ类取Tx=Ty=1.0;对Ⅲ、Ⅳ类按GBJ 17—1988中采用;ηEM为强度折减系数,若为Ⅰ、Ⅱ类ηEM=0.85,若为Ⅲ、Ⅳ类ηEM=0.90,当N/An≥0.55fy时,取ηEM=ηn.

总挠度ωT取值,可按下式确定:

(1)

式中:ω0为期载荷作用下,加固前的初始挠度;Δω为加载至破坏,挠度增大值,按相关规定计算.ωT值不大于GBJ 17—1988中的限值.

从表2和表3可知,构件承受静载时,两个规范在计算公式中都没有忽略塑性变形后的应力重分布现象,对相应的钢材进行强度的折减;构件承受动力载荷时,CECS 77∶1996对钢材强度乘以降低系数,强度计算时,取加固构件截面中强度最低的钢材来进行计算,YB 9257—1996规范采用原构件截面边缘屈服原则,对钢材强度没有进行折减.

3.2整体稳定计算

YB 9257—96规定:轴心受压时,加固柱构件的稳定性验算公式见表4.

表4　稳定计算公式

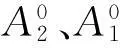
《钢结构加固技术规范》(CECS 77∶1996)规定:实腹式轴心受压构件,其整体稳定性计算公式:

(2)

式中:Nu为加固前、后构件承担的总轴向载荷;A为构件加固后的截面面积;φ为构件稳定系数,按GBJ 17—88中相应钢材的C类截面系数屈服强度表格查取,或用公式计算(计算时取fy=1.1f*);f*为钢材换算强度设计值.

当f0≤fs≤1.15f0时,取

(3)

当 1.15f0

(4)

式中:A0,A1分别为原构件面积、新增加的面积;f0,f1分别为原构件强度设计值、新增钢材的强度设计值; I0,I1分别为原构件截面、新增截面对加固后截面形心轴的惯性矩.

验算构件稳定性时,CECS77∶1996采用的是换算强度,对加固后组合构件稳定性系数,统一按照C类截面进行查表取值.YB9257—1996依然取原钢材强度设计值,加固后稳定系数取值和加固前相同,都是按照GB50017—2003中对应规定选取.

4负载下加固钢柱轴压承载力计算

为方便地计算负载下外包混凝土加固柱的承载力,参考各国学者对混凝土结构加固试验的研究,将混凝土和钢筋的强度折减系数的计算公式推导如下:

(1) 加固前

(5)

式中:N1为加固前原柱承受载荷值;Ass为型钢的有效净面积;εssu为原钢结构柱极限压应变;εss1为加固前型钢柱已有的压应变;fssu为型钢极限抗压强度;ρss为加固前原钢柱的稳定系数.

(2) 加固柱破坏后

(6)

(7)

式中:αy为纵筋强度折减系数,当αy>1时,说明钢筋已屈服,取αy=1;αc为混凝土强度折减系数;Ey为纵向钢筋的弹性模量.

将式(6)、(7)带入式(8),可得到加固柱的承载力计算公式:

(8)

式中:Nmax为加固柱最终极限承载力;fy为纵向钢筋抗压屈服强度;fc为混凝土抗压强度;As、Ac分别为纵向受压钢筋、混凝土的净截面积;φ为加固柱的整体稳定系数.

该式与CECS77∶1996和YB9257—1996这两个规范中规定进行对比,可知αy和αc值是随着β的变化而变化的,而不是取定值0.8.

5结论

(1) 两个规范中持载下四周包裹钢筋混凝土加固钢构件的初始应力水平指标的规定存在较大的差异.

(2) 负载状态下,钢结构加固后构件的承载力计算有两种原则:一是按加固后截面屈服原则进行计算;二是按原有构件截面边缘屈服准则进行计算,且对构件强度进行一定折减.

(3) 本文推导的加固柱的承载力计算方法与规范中计算方法对比说明,加固柱正截面承载力计算方法需等进一步研究改进.

参考文献:

[1] 贡金鑫,赵国藩,柳林. 钢筋混凝土轴心受压构件加固后的可靠度分析[J]. 建筑结构, 2000,30(3):29-33.

(GONGJX,ZHAOGF,LiuLL.Reliabilityanalysisofreinforcedconcreteaxiallycompressedmembersafterrehabilitation[J].BuildingStructure, 2000,30(3):29-33.)

[2] 刘威. 初始应力对轴心受压构件加固后承载力影响的研究[D]. 山东:中国海洋大学, 2013.

(LIU W. Study on the effect of initial stress on bearing capacity of strengthened structure members subjected to axial compression[D]. Shandong: The Ocean University of China, 2013.)

[3] YB 9257—1996钢结构检测评定及加固技术规程[S]. 北京:冶金工业出版社, 2002.

(YB 9257-1996 Technical specification for inspection,assessment and strengthening of steel structures[S]. Beijing: Metallurgical Industry Press, 2002.)

[4] CECS 77:1996钢结构加固技术规范[S]. 北京: 中国计划出版社, 2005.

(CECS 77:1996 Technical specification for strengthening steel structures[S]. Beijing: China Planning Press, 2005.)

[5] 俞国音,杨建平. 新编《钢结构检测评定及加固技术规程》 (YB 9257—1996)介绍(1)[J]. 钢结构, 1997,12(4):11-19.

(YU G Y, YANG J P. Introduction of (YB 9257—1996 Technical specification for inspection assessment and strengthening of steel structures0[J]. Steel Structure, 1997,12(4):11-19.)

[6] 祝瑞祥,王元清,戴国欣,等. 负载下钢结构构件增大截面加固设计方法对比分析[J]. 四川建筑科学研究, 2014,40(1):98-103.

(ZHU R X,WANG Y Q,DAI G X, et al. Comparative study on design methods for steel structural members strengthened by increasing the section area while under load in different codes,2014,40(1):98-103.(in Chinese))

[7] 苏钢结构设计研究联合公司. 改建企业钢结构加固时计算建议[G]. 冶金工业部建筑研究总院,译, 1987.

(Su steel Structure Design Research Associates. Suggestions in reconstructing reinforcement steel structure calculation[G]. Ministry of Metallurgical Industry Building Research Institute, Trans., 1987.)

[8] 周乐,王军伟,聂晓梅. 中短冷弯薄壁轴压构件承载力计算[J]. 沈阳大学学报(自然科学版), 2014,26(4):301-305.

(ZHOU L, WANG J W, NIE X M. Capacity of calculation theory of cold-formed thin-wall steel under axial compression about short and middle members[J]. Journal of Shenyang University (Natural Science), 2014, 26(4):301-305.)

[9] 凌程建. 工业厂房加固方法研究与实际应用[D]. 成都: 四川大学, 2006.

(LING C J. The research and practical application of industrial building reinforcement method[D]. Chengdu: Sichuan University, 2006.)

[10] NAGARAJA R N R,TALL L. Columns reinforced underload[R]. Fritz Laboratory Report No.286.1.Bethlehem,PA: Lehigh University. Fritz Engineering Laboratory Department of Civil Engineering, 1962:1-49.

[11] GB 50017—2003钢结构设计规范[S]. 北京: 中国计划出版社, 2003.

(GB 50017—2003 Code for design of steel structures[S]. Beijing: China Planning Press, 2003.)

[12] 刘声扬,王汝恒. 钢结构原理与设计[M]. 武汉:武汉理工大学出版社, 2010.

(LIU S Y,WANG R H. The fundamental theory of steel structures[M]. Wuhan: Wuhan University of Science and Technology Press, 2007.)

[13] 周玲. 外包混凝土加固钢柱的有限元分析[D]. 上海:上海交通大学, 2004.

(ZHOU L. Numerical Analysis of steel column strengthened with enclosed reinforced concrete[D]. Shanghai: Shanghai Jiaotong University, 2004.)

【责任编辑: 祝颖】

Calculation Theory of Bearing Capacity under Axial Compression after Reinforcement

ZhouLe,WangKeyao,NieXiaomei,YiJunwei,NiuPeng

(School of Architecture and Civil Engineering, Shenyang University, Shenyang 110044, China)

Abstract:In order to further study the calculation method of axial strengthening steel column, two standards of reinforcement technology are analyzed. The results show that : the initial stress level of reinforced column is limited to ensure reliability under load; two specifications are followed the original component whole cross section after section edge to yield and total cross-section yield after reinforcement; Under static load, both specification section consider stress redistribution after plastic deformation, but do not consider the stress redistribution under dynamic load and not consider the stress-strain lead or lag phenomenon of reinforced column.

Key words:design procedures; reinforced column; under load; the initial stress level indicator

中图分类号:TU 375

文献标志码:A

文章编号:2095-5456(2016)02-0151-04

作者简介:周乐(1978-),女,辽宁营口人,沈阳大学副教授,博士后研究人员.

基金项目:国家自然科学基金资助项目(51408371); 辽宁省自然科学基金资助项目(2014020098); 沈阳市科学技术计划项目(F14-196-4-00); 辽宁省高校优秀人才第二层次支持计划资助项目(2012230005).

收稿日期:2015-05-08