一种油气井用双向传爆管极限传爆距离

彭加斌, 肖 勇, 段嘉庆, 张明哲, 张 龙, 朱伟龙

(西安物华巨能爆破器材有限责任公司, 陕西 西安 710061)

1 引 言

在油气井聚能射孔中，为了确保射孔枪之间爆轰波的有效传递，通常需要一种传爆火工品——双向传爆管。该传爆管是仅装猛炸药且一端封闭的金属管。射孔枪之间的爆轰传递就是通过这种双向传爆管实现的。该双向传爆管一直在油气井射孔作业中被广泛应用。然而，由于井下温度往往远高于地面，导致射孔枪之间的两个双向传爆管彼此拉开一定距离，当两个传爆管之间的空气间隙增大到一定程度时会降低传爆管的传爆可靠性，造成施工失败。因此，双向传爆管之间的空气间隙大小(即传爆距离)是影响传爆管可靠传爆的关键因素之一。为此， 很多技术人员在如何提高双向传爆管传爆能力方面做过不少研究，周曌等[1]从双向传爆管的装药直径、装药高度、管壳壁厚与材质等的角度研究了影响传爆管性能的因素，向旭等[2]从双向传爆管管底厚度、传爆管间距、装药密度、使用的环境温度、装药类型和轴向偏心距离等的角度探索了影响双向传爆管传爆性能的诸多因素。他们只对影响传爆管传爆性能的诸多因素进行了定性研究和探讨，都没有对这种传爆管在空气中的极限传爆距离进行研究。由于这种传爆距离非常重要，因此中国能源部颁发的油气井用传爆管行业标准(SY/T 6753-2009)规定了该传爆管的传爆距离不小于50 mm，这种规定是站在施工角度，对双向传爆管提出来的基本要求，其缺乏试验和理论的依据，目前尚未见到这方面的论证研究报道。笔者采用火工品常用的感度试验用数理统计方法——升降法(GJB/Z 377A-1994)，对双向传爆管进行传爆实验，得到了对目前应用最广泛的双向传爆管在空气中的极限传爆距离(即在置信水平0.95下，可靠度为99.9%的传爆距离)，对该双向传爆管的传爆过程、机理进行了数值模拟，对实验得出的极限传爆距离结果给予理论上支持。

2 实验研究

2.1 实验材料

油气井用双向传爆管、油气井用导爆索、8#工业雷管、模拟实验用钢条、模拟实验用铝棒、25 m导线、起爆器、胶带、直尺等。

2.2 实验方法

双向传爆管在射孔枪中的传爆情形，如图1所示。其原理为: 每节射孔枪中的导爆索两端分别与双向传爆管连接，然后将相邻两支枪的双向传爆管分别放入联枪接头传爆孔内，若射孔枪A发生爆炸，则其内的导爆索引爆与之相连的双向传爆管，该双向传爆管爆炸，并将与之有一定距离的连在另一支枪导爆索上的双向传爆管引爆，此双向传爆管再起爆与之相连的导爆索，导爆索再引爆射孔枪B ，将一支枪内爆轰波传递给另一支射孔枪，从而使数百支串联的射孔枪依次稳定爆轰下去。由于这两个传爆管结构完全相同，因此不管爆轰波从哪个方向过来，都能通过这种传爆管进行枪间传爆，从而实现油气井射孔工艺中要求的所谓“双向传爆”功能。

本实验模拟射孔枪中双向传爆管传爆的方法进行实验，如图2所示。先将一个双向传爆管(以下称“施主传爆管”)与导爆索进行连接，然后将该传爆管用胶带固定在实验用钢条直线沟槽中，同样将另一双向传爆管(以下称“受主传爆管”)用胶带固定在该实验用钢条同一直线沟槽中，受主传爆管封闭端面朝向施主传爆管封闭端面，两封闭端面之间的传爆距离为D，用胶带将8#工业雷管与导爆索连接，通过导线将雷管与起爆器连接，起爆后观察受主传爆管是否爆炸。

图1射孔枪中双向传爆管

1—射孔枪A, 2—枪接头A, 3—导爆索, 4—双向传爆管, 5—枪接头B, 6—射孔枪B

Fig.1The bi-directional boosters in a string of perforator

1—perforator A, 2—gun connection A, 3—detonating fuse, 4— bi-directional boosters, 5— gun connection B, 6— perforator B

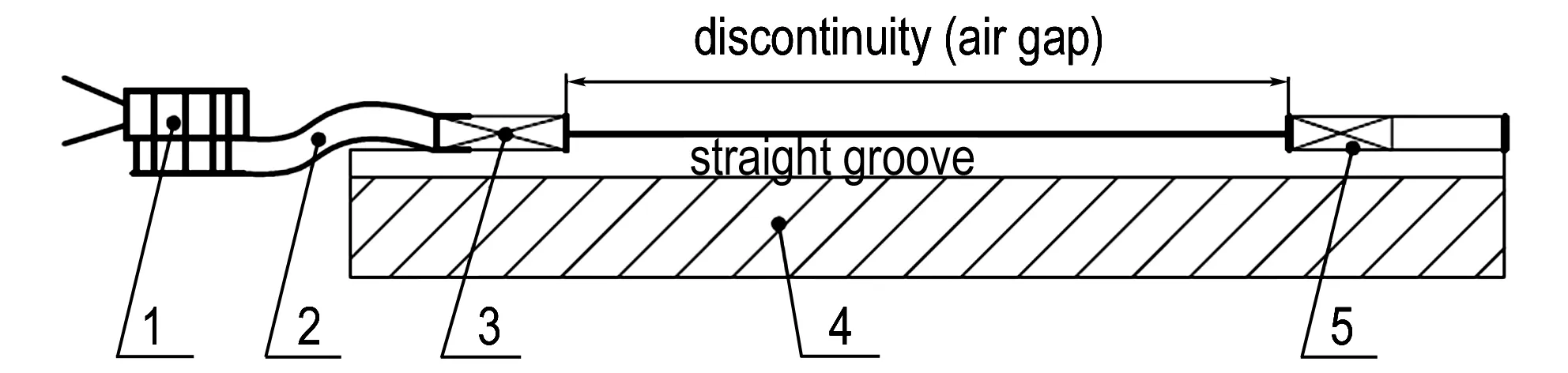
图2实验装置示意图

1—8#工业雷管, 2—导爆索, 3—施主传爆管, 4—钢条,5—受主传爆管

Fig.2Schematic diagram of the experimental device

1—8#industrial detonator, 2—detonating fuse, 3—donor booster, 4—steel bar, 5—acceptor booster

2.3 实验结果

据试验经验[1-2]知，该方式的传爆距离临界值近似服从正态分布，因此笔者采用火工品常用的感度试验用数理统计方法——升降法(GJB/Z 377A-1994)对双向传爆管临界传爆距离(即该传爆管的撞击感度)进行测试。由于传爆距离越大，传爆成功的概率越小，为了使刺激量取正值，选一个充分大的数L。根据以往大量试验结果，距离大于250 mm时肯定不会传爆成功，因此取L=250 mm，设D为施主和受主传爆管封闭端面之间的距离，得受主传爆管的新刺激量:x=250-D，由于传爆管撞击感度近似服从正态分布，故无需进行正态变换。由经验知，其50%临界传爆距离大约在110 mm，标准差d约为10 mm，取x0=250-110=140 mm，d=10 mm，定出试验用刺激量:xi=x0±id(i=0，±1，±2，…)。试验结果见表1。通过数据分析处理，得出: 双向传爆管在置信水平γ=0.95下，可靠度为50%的传爆距离估计值为114.3 mm、可靠度为0.1%的传爆距离估计值为145.5 mm，可靠度为99.9%的传爆距离(即极限传爆距离)估计值为82.8 mm。

表1双向传爆管传爆的实验结果

Table1Testing results of the bi-directional booster transmitting detonation

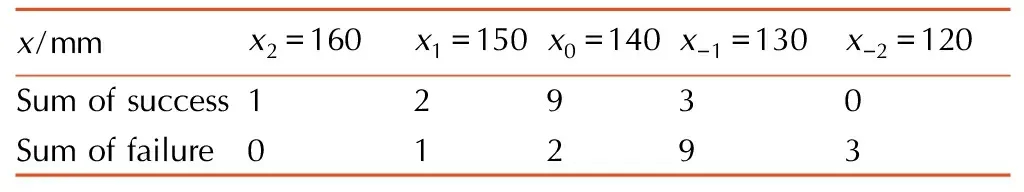
x/mmx2=160x1=150x0=140x-1=130x-2=120Sumofsuccess12930Sumoffailure01293

3 数值模拟

3.1 算法介绍

采用Ls-dyna软件对传爆管的爆炸过程进行数值模拟，采用的算法包括拉格朗日算法和SPH算法两种。

拉格朗日(Lagrange)算法多应用于固体力学求解中，网格固定在物体上随物体一起运动，适用于变形不太大的固体。对于物体的大变形问题，可以添加侵蚀算法，将大变形网格自动删除，从而避免网格严重变形扭曲产生的时间步小、负体积甚至计算停止等问题。

SPH(smoothed particle hydrodynamics)是一种常见的无网格粒子方法。该方法能通过核函数近似方法以及粒子离散方法将连续的控制方程转换成离散形式的控制方程。该方法不但适用范围广，而且在处理极大变形问题时有独特的优势。作为无网格算法，SPH方法既自然避免了网格严重变形的问题又可以保证材料质量完全不损失，这对于模拟破片形成及统计破片质量是非常有帮助的。

3.2 初始条件

传爆管壳总长37 mm，外径7 mm，壁厚0.25 mm，封闭端壳底厚度0.25 mm; 药柱长度为20 mm，直径为6.4 mm。

3.3 材料模型、状态方程及算法选择

炸药为HMX，采用高能炸药材料模型(MAT_HIGH_EXPLOSIVE_BURN)，密度为1.6 g·cm-3，爆速为8333 m·s-1，爆压为32.46 GPa，爆轰过程采用JWL状态方程描述[3, 6]，计算采用SPH算法[3-5]，模型共有粒子126400个; 整个传爆管壳为金属铝材料，除封闭端壳底外的部分采用等向随动强化材料模型(Mat-Plastic-Kinematic)[7]，材料密度为2.77 g·cm-3，该部分模型采用SOLID164实体单元划分网格，沿径向划分为两层，共有8568个单元，计算采用拉格朗日算法; 管壳封闭端壳底为金属铝材料，采用JOHNSON_COOK材料模型[8-9]，密度为2.77 g·cm-3， 配以GRUNEISEN状态方程描述，该部分壳体仍采用SPH算法[3-5]，粒子数为14140个。建模采用全模型，整体模型的不对称剖面显示图见图3。

为模拟除封闭端壳底外的管壳部分的破裂过程，炸药和该部分壳体之间采用自动点面接触，其关键字为CONTACT_AUTOMATIC_NODES_TO_SURFACE[3]。为方便计算，整个爆炸过程设计在真空中进行; 选用药柱左端面均匀分布的9个点同时起爆以模拟面起爆。

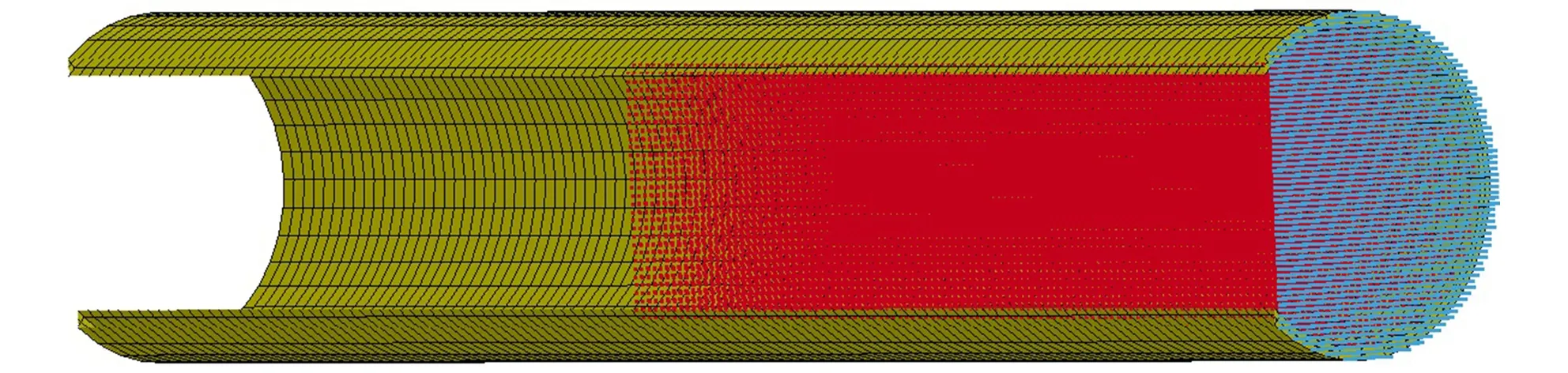
图3整体模型的不对称剖面图

Fig.3The asymmetric profile in one whole model

4 数值模拟结果及分析

4.1 施主传爆管爆炸过程

为方便显示起爆过程，隐藏了除封闭端壳底外的管壳部分的显示，施主传爆管爆炸过程见图4所示。每幅图右侧为沿轴向(爆轰波方向向)的右速度梯度标尺，单位m·s-1。从图4可看出，施主传爆管中的炸药在起爆后2.4 μs爆炸基本结束，之后,传爆管壳底(铝)在爆炸能量的作用下发生变形，在起爆10 μs时，传爆管壳底(铝)被爆炸产生的高压气体撕碎成大小不等的破片，同时破片已被高压气体加速成高速状态[10]，按一定方向各自飞散[11]。

图4施主传爆管爆炸过程模拟

Fig.4The simulation of donor booster exploding process

4.2 冲击波峰压及其变化

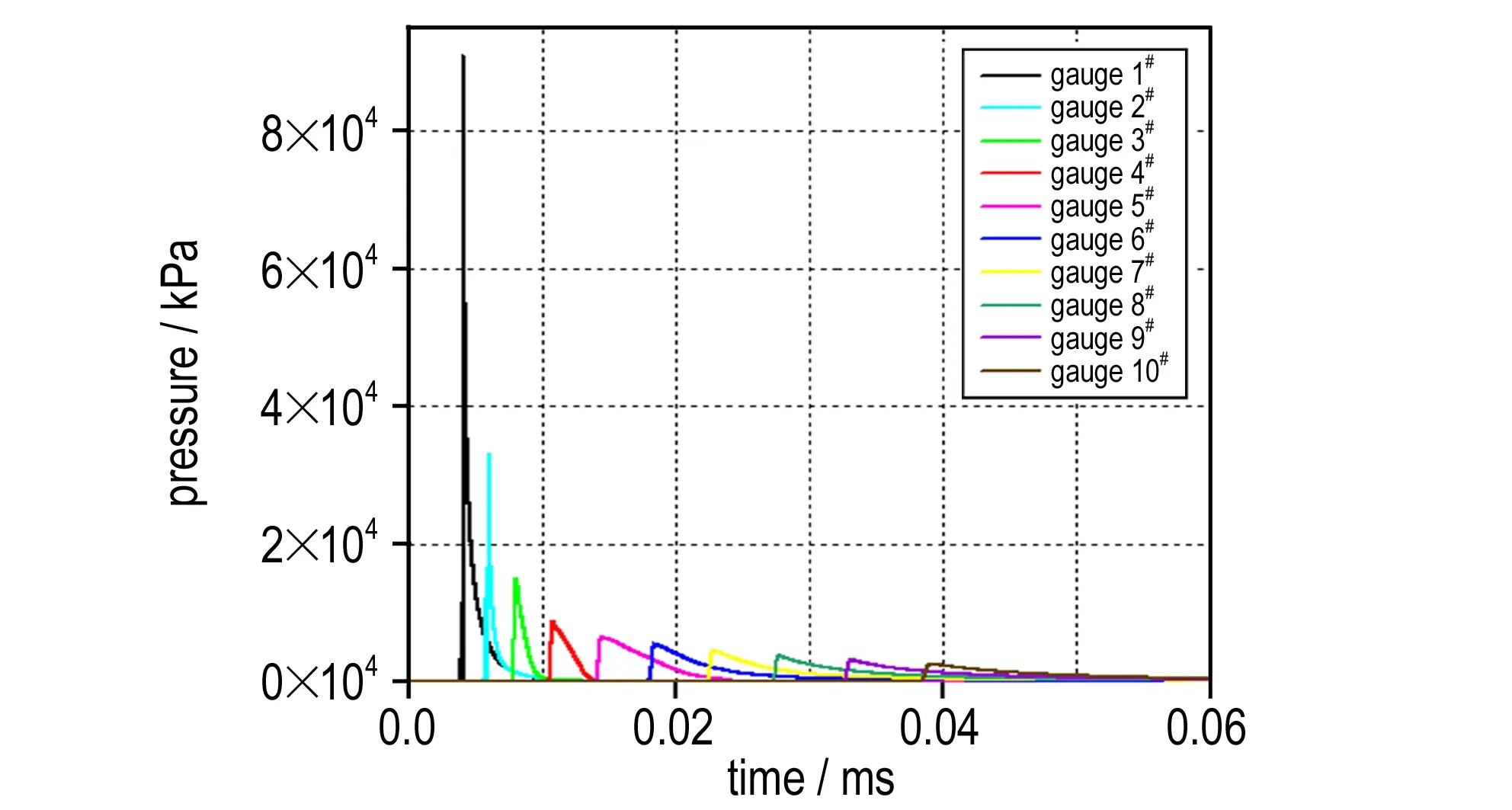
施主传爆管起爆受主传爆管的方式通常有两种: 冲击波起爆和破片起爆。建立空气当中炸药冲击波衰减的有限元模型(如图5a所示)，并在施主传爆管(忽略输出端壳体)输出端一侧不同距离处均匀设置10个测量点用以测量施主传爆管爆炸产生的冲击波在距施主传爆管右端面不同距离(单位mm)处的p-t曲线(如图5b所示)。从曲线可看出，距施主传爆管封闭端10 mm处的峰值压力为90 MPa左右，明显低于炸药临界起爆压力3 GPa以上[12-13]，之后各点的峰值压力依次降低，从而可以推断施主传爆管产生的冲击波不可能起爆受主传爆管。因此，10 mm处及更远的受主传爆管，其起爆只能由施主传爆管产生的破片高速撞击引起。

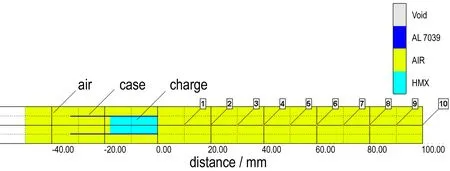
a. finite element model of detonation wave attenuation in the air and measuring points at different distances

b. pressure curves from measuring points at different distances

图5不同距离处炸药冲击波测量点的p-t曲线

Fig.5p-tcurves of the shock wave measurement point of explosive at the different distances

4.3 施主传爆管底端破片飞散和速率

由于施主与受主传爆管处于同轴线上，因此对受主传爆管起起爆作用的破片应该是施主壳底处产生的那部分。数值模拟可得到施主传爆管壳底(铝)被撕碎成大小不等的破片在离开端面不同距离时的分布情况，见图6。从图6可以看出，其轴芯周围的破片密度随破片飞行距离增大而变小，因此受主传爆管端面接受到的破片数量(或质量)随传爆距离的增大而减少。峰头破片(图6)速率随飞行距离的变化关系见图7。从图7可以看出，峰头破片速率在飞行10 mm以前就达到最大，即约4495 m·s-1，之后基本不变，这主要忽略了空气的影响所致，因此该速率较实际测量[14]的较大一些，且衰减更慢。但破片速率的变化规律与实际情况基本一致[15]。

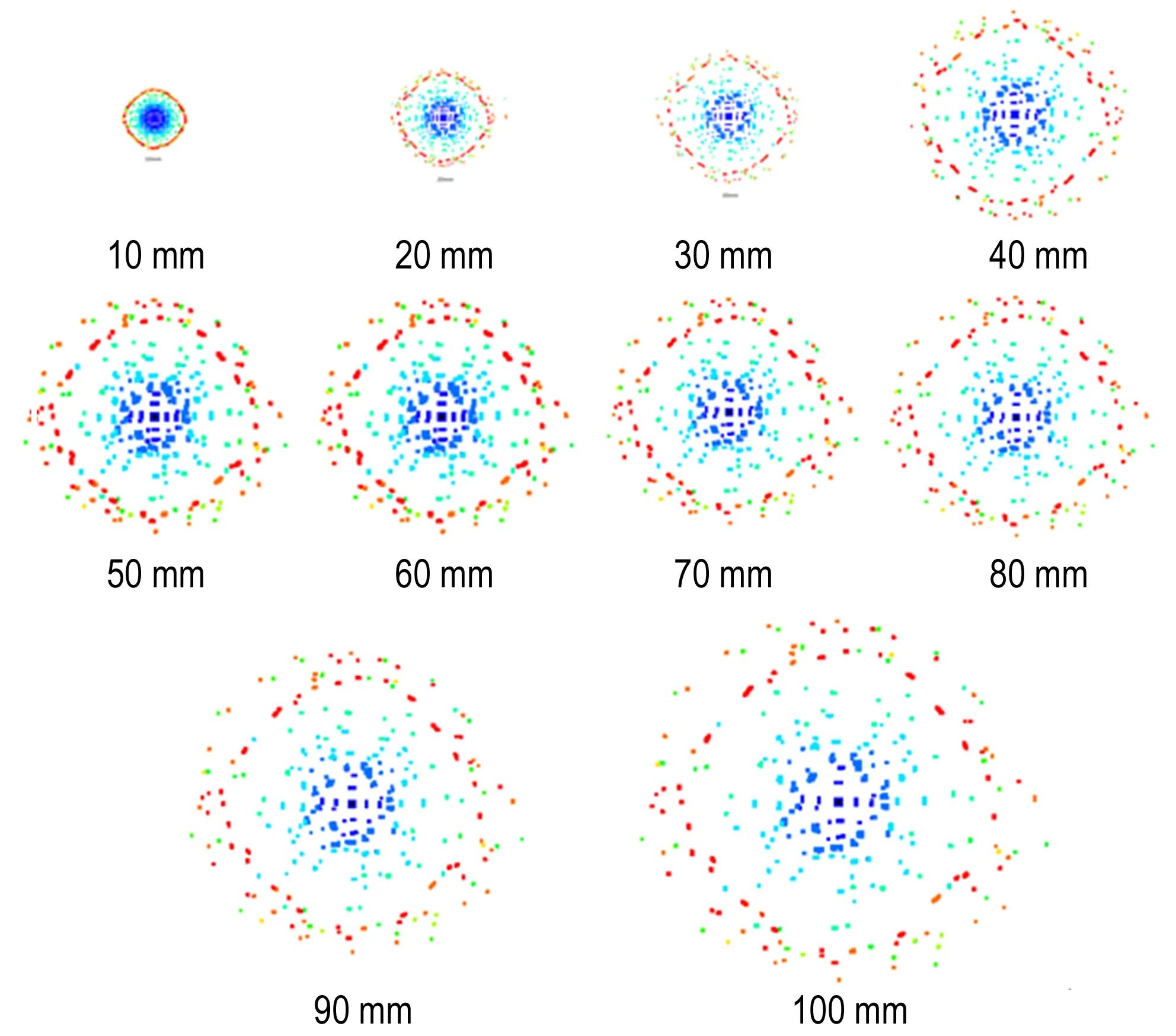
图6破片在离开端面不同距离时的正面截图

Fig.6Positive scattering of fragments at different distances away from the end face

4.4 受主传爆管封闭端面受到撞击的破片质量及撞击能

由于受主传爆管被起爆的成功率取决于撞击它的破片质量和速率(即撞击能)，因此通过数值模拟方法统计了受主传爆管封闭端面在不同传爆距离时受到撞击的破片质量(m)和该部分破片所携带的撞击能(1/2mv2，这里v取4495 m·s-1)，统计结果见表2。

图7峰头破片离开端面的距离与其速度的关系

Fig.7The distance and velocity of away from the end face for front fragments

表2受主传爆管封闭端面在不同传爆距离受到撞击的破片质量及撞击能

Table2Fragment mass of impacting the closed end face of acceptor booster at different transmitting detonation distances and its impact kinetic energy

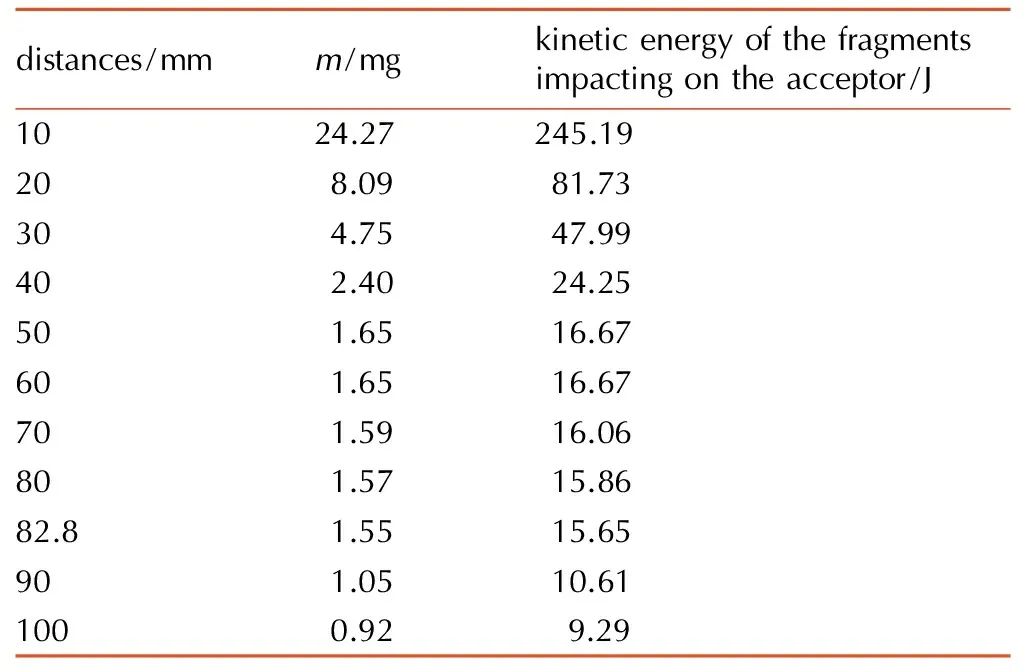
distances/mmm/mgkineticenergyofthefragmentsimpactingontheacceptor/J1024．27245．19208．0981．73304．7547．99402．4024．25501．6516．67601．6516．67701．5916．06801．5715．8682．81．5515．65901．0510．611000．92 9．29

Note:mis the mass of the fragments impacting on the accepter.

在统计破片质量时，由于SPH算法边界不清晰，不能直接读出破片质量，因此需要采用特殊方法进行统计。利用LS-PREPOST后处理功能，生成与传爆管同直径的圆柱辅助面及相应传爆距离的平面辅助面，并通过结果推进使破片与辅助圆柱面的交线刚好落在平面辅助面上(如图8a所示)，此时平面辅助面右侧为被统计破片(图8a中被圆柱面遮蔽)，然后利用Ident当中SPH元素统计功能，统计出平面辅助面右侧的SPH粒子数量(如图8b中白色部分)，最后通过粒子数量乘以单个粒子的质量(从模型K文件中找到)即可得到破片质量，该方法有效地统计了避免了SPH算法边界不清晰的缺陷，能较精确地统计出破片质量。从表2中可以发现该质量随着传爆距离的增加而不断减小，且在短距离段破片质量减小最快，相应地，破片能量的变化也呈现出同样规律。

a. method of capturing SPH particles by using auxiliary surfaces

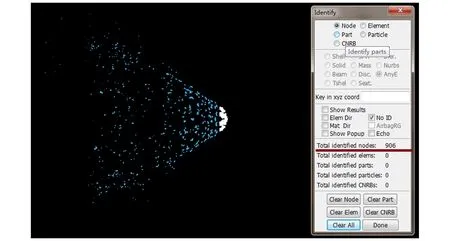
b. displayed number of captured SPH particles

图8运用LS-PREPOST统计破片质量方法演示图

Fig.8Displayed diagram of representation of statistic method of fragments′ mass by LS-PREPOST

HMX的99.9%(计数法)撞击发火的撞击能为8.37 J[16-17]，而表2显示，在82.8 mm处受主传爆管端面壳底接收破片的总撞击能为15.65 J，由于所有撞击破片的速度均按峰头值进行计算，且峰头速度比实际测量值大一些(因忽略了空气影响)，因此这里的总撞击能应该比实际值偏大。如果将高速破片在撞击受主传爆管端面壳体时所消耗的形变能从它的总撞击能去除，则最终受主传爆管端面炸药HMX接收到的净撞击能应趋近于8.37 J(或者说与8.37 J属同一量级)。因此，该传爆管数值模拟的结果在一定程度上支持了油气井用双向传爆管的极限传爆距离在82.8 mm左右的结论。

5 结 论

采用火工品常用的感度测试方法—升降法对双向传爆管进行了传爆试验，统计出了其极限传爆距离，并利用LS-DYNA软件对该传爆管的传爆过程和机理进行了数值模拟和探讨，得出如下结论:

(1) 在空气中，该油气井用双向传爆管之间的远距离(≥10 mm)传爆是通过施主传爆管底壳在爆炸高压作用下产生的高速破片撞击受主传爆管而实现的。

(2) 该油气井用双向传爆管在空气中的极限传爆距离在82.8 mm左右。

(3) LS-DYNA数值模拟得出的结果从理论上支持了油气井用双向传爆管的极限传爆距离在82.8 mm左右的实验结果。

参考文献:

[1] 周曌, 陈虹, 严瑞才, 等. 油、气井用高温传爆管的传爆影响因素探讨[J]. 火工品, 2003 (3): 39-41.

ZHOU Zhao, CHEN Hong, YAN Rui-cai, et al. Exploration on the influence factors of explosive transfer of heat-resistant booster for oil-gas well[J].Initiators&Pyrotechnics, 2003 (3): 39-41.

[2] 向旭, 赖康华. 油气井用传爆管性能影响因素探讨[J]. 测井技术, 2011, 35(4): 384-386.

XIANG Xu, LAI Kang-hua. Discussion on the influence factors on the booster tube for oil and gas wells[J].WellLoggingTechnology, 2011, 35(4): 384-386.

[3] 李利莎, 谢清粮, 郑全平, 等. 基于Lagrange_ALE和SPH算法的接触爆炸模拟计算[J]. 爆破, 2011, 28(1):18-22.

LI Li-sha, XIE Qing-lianag, ZHENG Quan-ping, et al. Numerical simulation of contact explosion based on lagrange ALE and SPH[J].Blasting, 2011, 28(1): 18-22.

[4] 周东强, 刘小虎. 节点分离法及其在高速碰撞中的应用研究[J]. 固体力学学报, 2008, 29(S): 49-52.

ZHOU Dong-qiang, LIU Xiao-hu. Study on nodal point separation algorithm and its application in hypervelocity impact problem[J].ChineseJournalofSolidMechanics, 2008, 29(S): 49-52.

[5] 张伟, 庞宝君, 贾斌, 等. 弹丸超高速撞击防护屏碎片云数值模拟[J]. 高压物理学报,2004,18(1): 47-52.

ZHANG Wei,PANG Bao-jun,JIA Bin,et al. Numerical simulation of debris cloud produced by hypervelocity impact of projectile on bumper[J].ChineseJournalofHighPressurePhysics, 2004, 18(1): 47-52.

[6] 李金铭, 马国伟, 马建. 间隔靶板对破甲战斗部威力影响的数值模拟[J]. 弹箭与制导学报, 2013,33(5): 112-114.

LI Jin-ming, MA Guo-wei, MA Jian. Numerical simulation of the effect of disconnected target on the power of armor-penetrating warhead[J].JournalofProjectilesRocketsMissilesandGuidance, 2013, 33(5): 112-114.

[7] 杨超, 杜来林. 基于ANSYS_LS_DYNA的有限元动力分析应用[J]. 机电产品开发与创新, 2011, 24(1): 121-125.

YANG Chao, DU Lai-lin. Finite element dynamic analysis and application on ANSYS/LS-DYNA[J].Development&InnovationofMachinery&ElectricalProducts, 2011, 24(1): 121-125.

[8] 白强本, 李向东, 贾飞, 等. 高速破片撞击飞机油箱的数值模拟研究[J]. 兵工自动化, 2014, 33(1): 35-38.

BAI Qiang-ben, LI Xiang-dong, JIA Fei, et al. numerical simulation on high-speed fragment impact against an aircraft fueltank[J].OrdnanceIndustryAutomation. 2014, 33(1): 35-38.

[9] 李旭锋, 李向东, 顾文彬, 等. 含能破片引爆带壳炸药过程的数值模拟[J]. 爆炸与冲击, 2014, 34(2): 202-207.

LI Xu-feng, LI Xiang-dong, GU Wen-bin, et al. Numerical simulation on detonating shelled explosion by energetic fragments[J].ExposionandShockWaves, 2014, 34(2): 202-207.

[10] 屈明, 钱立新. 破片发生器爆轰驱动数值模拟[J]. 含能材料,2003,11(2): 66-70.

QU Ming, QIAN Li-xin. Numerical simulation for detonation drive of fragment generator[J].ChineseJournalofEnergeticMaterials(HannengCailiao),2003,11(2): 66-70.

[11] 何广军, 万少松, 高福利. 防空导弹战斗部破片飞散特性分析[J]. 空军工程大学学报(自然科学版), 2000(4): 117-20.

HE Guang-jun, WAN Shao-song, GAO Fu-li. The Analysis on dispersion characteristic of aerial defense missile warhead[J].JournalofAirForceEngineeringUniversity(NaturalScienceEdition), 2000(4): 117-20.

[12] 李小笠, 屈明, 路中华. 三种破片对带壳炸药冲击起爆能力的数值分析[J]. 弹道学报, 2009, 21(4): 72-75.

LI Xiao-li, QU Ming, LU Zhong-hua. Numerical simulation on impact effect of three types fragments impacting steel-cover charge[J].JournalofBallistics, 2009, 21(4): 72-75.

[13] 梁斌, 冯高鹏, 魏雪婷. 多枚破片冲击引爆带盖板炸药数值模拟分析[J]. 弹箭与制导学报, 2013, 33(6): 62-66.

LIANG Bin, FENG Gao-peng, WEI Xue-ting. Numerical simulation on shock initiation composition explosive of cover board subjected to multi-fragment[J].ProjectilesRocketsMissilesandGuidance, 2013, 33(6): 62-66.

[14] 蒋小华, 陈静畴, 李敏, 等. 一种小型炸药驱动飞片装置的试验与数值模拟研究[J]. 含能材料, 2001, 18(6): 670-673.

JIANG Xiao-hua, CHEN Jing-chou, LI Min, et al. Experimental and numerical studies on flyer initiation device[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2001, 18(6): 670-673.

[15] 蔡瑞娇. 火工品设计原理[M]. 第一版. 北京: 北京理工大学出版社, 1999: 193-196.

CAI Rui-jiao. Theory of firework design[M]. Beijing: Beijing Technology College Press, 1999: 193-196.

[16] 王桂吉, 王平, 徐荣, 等. ANBDF炸药的短脉冲起爆感度研究[J]. 火工品, 2007(5): 20-22.

WANG Gui-ji,WANG Ping,XU Rong,et al. Study on short-duration pulse initiation sensitivity of ANBDF[J].Initiators&Pyrotechnics, 2007(5): 20-22.

[17] 袁俊明, 张庆明, 刘彦. 炸药感度测试兰利法与升降法比较研究[J]. 含能材料, 2008, 16(1): 86-89.

YUAN Jun-ming, ZhANG Qing-ming, LIU Yan. Comparison study on Langlie method and up and down method for sensitivity test of explosive[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2008, 16(1): 86-89.