三点起爆同步误差对尾翼EFP成型性能的影响
李 瑞, 李伟兵, 王晓鸣, 李文彬
(南京理工大学智能弹药技术国防重点实验室, 江苏 南京 210094)
1 引 言
爆炸成型弹丸(explosively formed projectile, EFP)具有远距离(有效炸高可达1000倍装药口径)攻击目标的能力,被广泛应用于反装甲武器。在EFP远距离飞行过程中,为了保证飞行弹道稳定并准确命中目标,对EFP的气动外形、飞行阻力及着靶精确度都提出了较高的要求[1]。尾翼EFP是通过一定的技术措施使EFP尾部发生规律性的褶皱,形成具有呈星形布置多个鳍状尾翼的特殊EFP,具有良好的空气动力稳定性和飞行弹道性能,适合于攻击远距离目标[2]。实现尾翼EFP方法有多种,研究表明采用多点同步起爆网络实现同步起爆是形成尾翼EFP一种简单可行的方式[3-5]。近年来,许多学者对多点同步起爆网络及其起爆精度做了大量的研究,如温玉全等[6]、白颖伟等[7]分别设计了刚性、柔性多点同步起爆网络,测量其同步误差分别为80 ns和200 ns; 沈慧铭等[8]设计一种板式结构的8点环形起爆器,其输出同步性为170 ns。研究表明,实际中多点起爆网络同步误差总是存在。而针对多点起爆同步误差对毁伤元成型的影响国内外也开展了大量研究,如李伟兵等[9-10]研究了6点起爆网络同步起爆精度对形成聚能侵彻体的速度、长径比等参数的影响规律,该研究主要基于小炸高情况下聚能侵彻体侵彻威力的考虑; 罗健等[11]在研究起爆点数对尾翼EFP的影响时,提出多点起爆的同步性对EFP的飞行稳定性有较大的影响,必须严格加以控制,但未对多点起爆的同步性对EFP成型参数的影响规律进行研究; D.Cardoso和F.Teixeira-Diasd[12]研究了起爆点数和起爆点位置对EFP成型参数的影响,但是没有考虑多点起爆同步偏差对EFP成型的影响,尤其是起爆精度对尾翼EFP成型有何影响有待研究。
本研究利用LS-DYNA非线性动力有限元软件,仿真研究三点起爆同步误差对尾翼EFP成型及飞行速度的影响,分析三点起爆EFP尾翼形成过程及三点同步起爆误差的影响原因,找出三点起爆成型装药形成较佳尾翼EFP应满足的最大同步起爆误差。为多点起爆形成远距离攻击目标的尾翼EFP毁伤元的相关研究、设计提供参考。
2 计算模型及数值模拟方案
本研究引用文献[13]形成尾翼EFP的成型装药结构,如图1所示,其中装药直径Dc=65 mm,装药长度Lc=32.5 mm,罩顶厚度δ=2.8 mm,药型罩外曲率半径为70 mm,内曲率半径为78 mm,采用端面三点环起爆,起爆环直径Di=40 mm。文献[13]试验验证了三点同时起爆形成规则尾翼EFP的可行性及仿真计算结果。有限元三维计算模型及起爆点分布如图2,主装药采用JH-2,用高能炸药材料模型和JWL状态方程描述,紫铜药型罩用Johnson_Cook本构模型和Gruneisen状态方程描述,具体计算参数见文献[13]。
在实际中多点起爆网络的起爆同步误差是参差不齐的,有一定的随机性,但是为了找出起爆同步误差对EFP尾翼成型的影响规律,将延迟起爆时间Δt分别设定为0,50,100,150,200,300,500 ns,将延迟起爆时间进行分配得到28种工况,如表1所示,其中设起爆点O1、O2、O3的延迟时间分别Δt1、Δt2、Δt3,三点同时起爆为工况n=0。
图1 装药结构示意图
Fig.1 Schematic diagram of EFP charger

图2 数值计算模型
Fig.2 A model for numerical simulation
表1 三点起爆同步误差分布
Table 1 Distribution of three-point initiation synchronization error

synchronizationerror/nsconditionn012345678910111213Δt100000000000000Δt20050050100050100150050100150Δt305050100100100150150150150200200200200synchronizationerror/nsconditionn1415161718192021222324252627Δt100000000000000Δt2200050100150200300050100150200300500Δt3200300300300300300300500500500500500500500
3 同步误差对尾翼EFP成型影响
3.1 带同步误差三点起爆对药型罩不对称压垮过程分析
为了分析带同步误差三点起爆引起药型罩不对称压垮过程,选取工况n=18的尾翼EFP成型过程进行分析。图3为装药端面起爆后形成的复合爆轰波对药型罩作用的压力等值线图。从图3中可以看出先后在O1、O2,O1、O3和O2、O3起爆点形成的半球面爆轰波两两碰撞处形成高压区,随后三个高压区相连,面积增大形成三叉形高压区。同等时间,三个半球面爆轰波对药型罩作用面积不相等,进而形成的三叉形高压区偏离了两两起爆点对称面。t=3.89 μs,3个半球面爆轰波碰撞作用点运动到三叉形高压区交点处的药型罩上,在药型罩上发生碰撞,在三叉形中心形成超高压作用区,超高压作用区对EFP头部形成至关重要。由于三个半球面爆轰波形成有先后,使得相同时间内形成的三个半球面爆轰波半径大小不同,进而三个半球面爆轰波碰撞叠加后形成的三叉形高压区偏离装药正中,三叉形中心的超高压作用区偏离装药中心轴线,作用偏离药型罩的顶点中心。t=4.59 μs,在三叉形靠近装药周边形成三个周边高压区,这三个周边高压区阻止EFP尾群向中心压合。
各起爆点形成的半球面爆轰波相互碰撞作用于药型罩表面形成三叉形高压区、三叉形中心超高压区以及周边高压区,对药型罩材料加载过程和初速度获得至关重要。图4为药型罩质点在不同时刻的速度等值线图,图4中181771点为药型罩顶点。图5为药型罩在不同时刻的变形。从图4看出药型罩先后在三个半球面爆轰波作用处获得速度,发生压垮(图5,t=7.20 μs); 随后药型罩先后在O1、O2,O1、O3和O2、O3起爆点形成的半球面爆轰波两两碰撞处形成的三叉形高压区的速度最大,表明药型罩在三叉形高压区先后形成三叉突起翻转(图5,t=14.99 μs); 接着药型罩在三叉形中心的超高压区处速度达到最大,表明药型罩在三叉形中心超高压作用下发生拉伸(图5,t=64.99 μs)。从图4可以看出药型罩三叉形中心速度最大区域偏离药型罩中心点,表明超高压作用区偏离药型罩中心。药型罩尾翼质点速度相对较低向中心轴线压合,而三叉形靠近药型罩周边在三个周边高压区作用下阻止向中心轴线压合,最后形成尾翼EFP(图5,t=90.01 μs)。

图3 不同时刻爆轰波阵面的压力等值线(单位: 102GPa)
Fig.3 Pressure isolines of detonation wave at different times (unit: 102GPa)

图4 不同时刻药型罩质点的速度等值线(单位: 104m·s-1)
Fig.4 Nodal velocity isolines of liner at different times (unit: 104m·s-1)

图5 EFP成型过程的数值计算结果
Fig.5 Simulated results of the forming process of EFP
从图4中可以看出,药型罩在三叉形中心超高压区作用下速度达到最大,发生拉伸形成尾翼EFP头部。由于三叉形中心超高压区偏离药型罩中心,导致最终形成的EFP尾翼外形不规则,外形不规则的EFP尾翼在飞行过程中受到空气阻力不均匀,导致空气动力不稳定,攻击远距离目标会偏离预定轨道。试验也表明多点同步起爆网络存在同步误差下形成的EFP形状不完全对称[11]。
3.2 不同工况下EFP尾翼成型情况分析
数值计算过程中,三点起爆同步误差按表1依次进行模拟,考虑只存在一点起爆偏差的工况,分别取工况n=0、1、3、6、10、15、21进行分析。图6为外形稳定时刻尾翼EFP的正视图和底视图。
从图6可以看出,工况n=0,三点同时起爆,EFP成型规则,EFP尾翼形成规则的褶皱。其他工况下,如果最大延迟时间在100 ns以内,三点起爆同步误差对EFP成型及尾翼形成的褶皱有影响,但形成的EFP及其尾翼较规则。当最大延迟时间大于100 ns,EFP开始成型不规则,EFP的尾翼也变的不规则。特别是到了300 ns,EFP发生严重不规则变形,底部尾翼也发生严重变形。
图6中可以看出起爆同步误差对EFP底部尾翼的成型影响较大,为此对不同工况下形成的EFP尾翼翼长进行测量并进行标准差分析。测量示意图如图7,三个较大尾群(外侧尾翼)翼长分别为A1、A2、A3,三个较小尾群(内侧尾翼)翼长分别为a1、a2、a3。
只存在一点起爆偏差工况下的三个外侧尾翼和三个内侧尾翼翼长标准差分析结果如图8所示。可以看出最大延迟时间在100 ns以内,内、外侧尾翼翼长偏差都较小,说明形成的EFP尾翼较规则; 当最大延迟时间从100 ns到150 ns,内、外侧尾翼翼长偏差增大了113.1%,对EFP的尾翼对称性产生了一些影响; 而当延迟时间从150 ns到200 ns,内侧尾翼翼长偏差增大了215.6%,外侧尾翼翼长偏差增大了74.8%,对EFP的尾翼对称性产生了较大的影响; 特别当延迟时间大于200 ns以后,内、外侧尾翼长度偏差发生剧烈变化,说明形成的尾翼变的不规则,这势必影响EFP的飞行稳定性。

图6 不同工况下形成的尾翼EFP外形
Fig.6 Shapes of EFP with fins formed by different condition
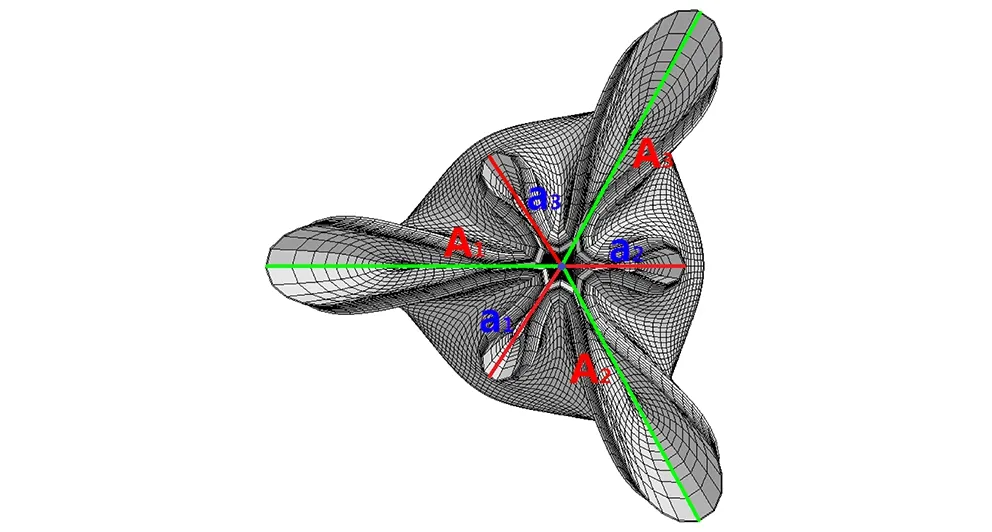
图7 尾翼翼长示意图
Fig.7 Schematic diagram of empennage lengths

图8 一点起爆偏差工况下形成的EFP尾翼翼长偏差
Fig.8 EFP empennage length deviation with the error of one initiation point
对于表1中设定的起爆偏差工况n=2、5、9、14、20、27,选取两点存在相同起爆偏差,实际上等同于存在一点起爆偏差的工况,同理获得了其内、外侧尾翼翼长的偏差和稳定时刻尾翼EFP的底视图(见图9),内、外侧尾翼翼长的偏差随起爆偏差的变化规律与图8变化规律一致。
对表1中所有工况下尾翼翼长进行统计分析,如图10所示。可以看出最大延迟时间在100 ns以内,内、外尾翼翼长的偏差较小,形成的尾翼较规则。延迟时间大于100 ns后,偏差变大,尾翼变的不规则,影响其远距离飞行空气动力稳定。因此,三点起爆同步误差应控制在100 ns范围内,这样形成的EFP尾翼规则,保证形成的尾翼EFP飞行稳定。

图9 两点相同起爆偏差工况下形成的EFP尾翼外形和翼长偏差
Fig.9 EFP empennage shapes and length deviation with the error of two simultaneous initiation point

a. outer empennage length

b. inner empennage length
图10 不同工况下形成的EFP尾翼翼长
Fig.10 EFP empennage length by different condition
3.3 同步误差对尾翼EFP飞行速度的影响
尾翼EFP形成的飞行速度v在空间坐标系分成两个分速度: 沿装药轴线速度分量为竖直分速度vz,垂直于装药轴线方向为水平分速度vx-y。竖直分速度vz是保证形成的尾翼EFP向前飞行,而水平分速度会使形成的尾翼EFP偏离预定轨道,对远距离攻击目标不利。图11为28种工况下,尾翼EFP稳定后飞行的速度分量vx-y、vz。

a. vx-y

b. vz
图11 不同工况下尾翼EFP飞行速度
Fig.11 Velocity of EFP with fins by different conditions
从图11中可以看出随着最大延迟时间增加,水平分速度vx-y增大,不利于形成的尾翼EFP远距离飞行,竖直分速度vz减小,最大只减少0.21%,说明起爆误差的存在对EFP向前飞行速度影响较小。在图11a中,Δt2在0~Δt3范围内,水平分速度vx-y呈抛物线规律变化,相应的拟合曲线如下:
当(1)~(5)式中的Δt2分别为51.54,74.03,97.26,141.03,216.89 ns,vx-y取最小值,可以看出Δt2≈Δt3/2时,水平分速度最低。因此,三点起爆应尽量使中间起爆点误差为最大误差的一半,这样可以减小水平分速度。在图11b中可以看出,当Δt2在0~Δt3/2范围内,竖直分速度vz略有降低,当Δt2在Δt3/2~Δt3范围内,竖直分速度vz降低较大。因此,在实践中应尽量使中间起爆点误差约为最大同步误差的一半,这样可以减小水平分速度,增大形成的尾翼EFP飞行稳定性。
4 结 论
(1) 三叉形高压区和三叉形中心超高压区对尾翼EFP成型至关重要。由于起爆同步误差的存在,三叉形高压作用区偏离药型罩正中,三叉形中心超高压区偏离药型罩中心,使得尾翼EFP成型不规则。
(2) 最大延迟时间在100 ns以内时,内外侧尾翼翼长偏差都较小,三点同步起爆误差对EFP尾翼成型影响较小; 最大延迟时间大于100 ns后,内外侧尾翼翼长偏差不断增大,形成的EFP尾翼发生不规则变化,这势必影响EFP的飞行稳定性。因此,三点同步起爆网络各起爆点的同步误差应控制在100 ns内。
(3) 随着最大延迟时间增加,竖直分速度减小,最大只减少0.21%,说明起爆误差对EFP前行速度影响较小,但水平分速度vx-y增大,不利于形成的尾翼EFP远距离飞行,因此要控制起爆同步误差。实际过程中尽量使中间起爆点误差约为最大误差的一半,有利于降低水平分速度。
参考文献:
[1] Bender D, Chhouk B, Fong R, et al. Explosively formed penetrators (EFP) with canted fins[C]∥Proceedings of the 19th International Symposium on Ballistics, Casino. Kursaal Congress Center, Interlaken, Switzerland, 2001: 755-762.
[2] LIU Jian-qing, GU Wen-bin, LU Ming, et al. Formation of explosively formed penetrator with fins and its flight characteristics[J].DefenceTechnology, 2014, 10: 119-123.
[3] Bouet T H, Tarayre P, Guillon J P. Study of a multi-point ignition EFP[C]∥Proceedings of the 15th International Symposium on Ballistics. Jerusalem, Israel, 1995: 159-166.
[4] LI Cheng-bing, SHEN Zhao-wu, PEI Ming-jing. Investigation of three-point detonation mechanism and formation of tails of EFP[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2007, 15(1): 23-28.
[5] 刘建青, 顾文彬, 徐浩铭, 等.多点起爆装药结构参数对尾翼EFP成型的影响[J]. 含能材料, 2014, 22(5): 594-599.
LIU Jian-qing, GU Wen-bin, XU Hao-ming, et al. Effects of multi-point initiation charge configuration parameters on EFP with fins formation[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2014, 22(5): 594-599.
[6] 温玉全, 焦清介.同步起爆网络精密压装装药技术研究[J]. 兵工学报, 2006, 27(3): 410-413.
WEN Yu-quan, JIAO Qing-jie. A study on the precision press loading technique of a synchronous multi-point explosive circuit[J].ActaArmamentarii, 2006, 27(3): 410-413.
[7] 白颖伟, 张蕊, 李哲, 等. 柔性多点同步爆炸网络设计技术研究[J]. 含能材料, 2009, 17(2): 225-228.
BAI Ying-wei, ZHANG Rui, LI Zhe, et al. Design on mild multi-point synchronous explosive circuit[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17(2): 225-228.
[8] 沈慧铭, 李伟兵, 王晓鸣, 等. 多点起爆网络结构参数设计及其同步误差分析[J]. 含能材料, 2016, 24(3): 238-243.
SHEN Hui-ming, LI Wei-bing, WANG Xiao-ming, et al. Design and synchronization analysis of structural parameter of a multi point explosive circuit[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2016, 24(3): 238-243.
[9] 李伟兵, 王晓鸣, 李文彬, 等. 环形多点起爆精度对聚能杆式侵彻体成型的影响[J]. 爆炸与冲击, 2010, 30(1): 45-50.
LI Wei-bing, WANG Xiao-ming, LI Wen-bin, et al. Effects of annulus multi-point initiation precision on formation of jetting projectile charge[J].ExplosionandShockWaves, 2010, 30(1): 45-50.
[10] LI Wei-bing, WANG Xiao-ming, LI Wen-bin. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator[J].InternationalJournalofImpactEngineering, 2010, 37: 414-424.
[11] 罗健, 蒋建伟, 朱宝祥. 多点起爆对EFP形成的影响研究[J].弹箭与制导学报, 2004, 24(2): 27-29.
LUO Jian, JIANGJian-wei, ZHU Bao-xiang. The effect of multi-point initiation on the explosively formed penetrator formation[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2004, 24(2): 27-29.
[12] Cardoso D, Teixeira-Dias F. Modelling the formation of explosively formed projectile (EFP)[J].InternationalJournalofImpactEngineering, 2016, 93: 116-127.
[13] 刘建青, 郭涛, 顾文彬, 等. 三点起爆形成尾翼的数值模拟和实验研究[J]. 爆炸与冲击, 2013, 33(1): 38-46.
LIU Jian-qing, GUO Tao, GU Wen-bin, et al. Numerical simulation and experimental investigation of EFPs with fins formed by three point initiation[J].ExplosionandShockWaves, 2013, 33(1): 38-46.

