一类广义的Cauchy行列式
王晓元,刘海霞(大连交通大学理学院,辽宁大连116028)*
一类广义的Cauchy行列式
王晓元,刘海霞
(大连交通大学理学院,辽宁大连116028)*
利用Laplace展开公式证明了一类广义的Cauchy行列式,并利用差商运算给出几个有趣的Cauchy行列式的推广形式.
Cauchy行列式; Laplace展开公式;差商
0 引言
行列式的计算一直是代数学研究的一个重要课题,倍受着数学家和物理学家的关注.著名的Cauchy行列式不仅在多重椭圆超几何级数中有着基本的应用,而且在对称函数理论中具有举足轻重的地位.为了更深入地研究这类行列式,本文将利用Laplace展开公式证明一类广义的Cauchy行列式公式,并在此基础上利用差商运算给出几个有趣的Cauchy行列式的推广形式

考虑到下面的应用,定义:

接下来,回顾一下差商的定义及性质,这部分内容可以参见Lascoux[6].对任意的复函数f( y)及不等距节点{ xk}nk =0,关于自变量y的差商运算定义如下:


通常情况下,可以将它表示成Newton公式:

1 一类广义的Cauchy行列式
在这一节,利用Laplace展开公式得到一个广义的Cauchy行列式公式.
定理1 (广义的Cauchy行列式)


证明 对式( 1)左端采用加边法,加入一行元素1,β0,β1,…,βn,一列元素1,0,…,0.将所得行列式的第一行的(-αi)倍加到第i行,并利用Laplace公式按第一行展开,有


将上式求和中的行列式,再次利用Laplace公式按第一列展开得

最后,利用Cauchy行列式将上式展开,得到

将上式代入后,得到定理1.
推论1在定理1中,令p0= 0,则有

推论2在定理1中,令p0= q0= 0,则有

2 应用
在这一节,令αi,pi和βj,qj分别是关于xi和yj的函数,通过对它们取不同的函数,并利用差商运算,我们可以得到下面几个有趣的Cauchy行列式的推广形式.
命题1在推论1中,令βk= 1,qk= 1-qyk,则有

证明 由推论1可以得到

将等式右端求和公式写成差商形式


再利用Chu[5]中式( 2.7),有

将上式代入得到命题1.
命题2 在推论1中,令βk= 1-βyk,qk= 1-qyk,则有

证明 由推论1可以得到

将等式右端求和公式写成差商形式

再利用Chu[5]中式( 2.7)和( 2.8),有
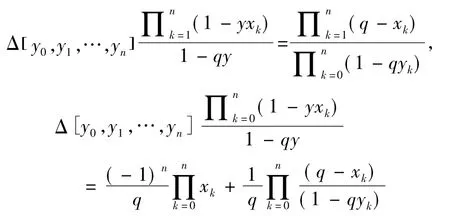
将上式代入得到命题2.
命题3在定理1中,令αk= a,βk= 1,pk= b,qk= 1,则有

证明 由定理1可以得到

将等式右端求和公式写成差商形式

将上式代入得到命题3.
命题4在定理1中,令αk= a,βk= 1,pk= 1-pxk,qk= 1,则有

证明 由定理1可以得到


将等式右端求和公式写成差商形式

将上式代入得到命题4.
[1]北京大学数学系几何与代数教研室代数小组.高等代数[M].3版,北京:高等教育出版社,2003.
[2]王萼芳.高等代数教程[M].北京:清华大学出版社,1997.
[3]周士藩.高等代数解题分析[M].江苏:江苏科技大学出版社,1985.
[4]王任宏.数值逼近[M].北京:高等教育出版社,1999.
[5]CHU W.The Cauchy double alternant and divided differences[J].Ctronic Journal of Linear Algebra,2006( 15) : 4-21.
[6]LASCOUX A.Symmetric Functions and Combinatorial Operators on Polynomials[C].CBMS Regional Conference Series in Mathmatics,AMS,2003.
The Generalizations of Cauchy’s Double Alternant
WANG Xiaoyuan,LIU Haixia
( School of Mathematics and Physics,Dalian Jiaotong University,Dalian 116028,China)
Applying the Laplace expansion formula,a generalization of the Cauchy determinant formula is established.Several interesting extensions of Cauchy determinant identities are derived as consequences by means of divided differences.
cauchy determinant; laplace expansion formula; divided differences
A
1673-9590( 2016) 01-0117-03
2015-04-07
王晓元( 1981-),女,副教授,博士,主要从事超几何级数与组合恒等式的研究
E-mail: xiaoyuan_djtu@163.com.

