基于不同目标的铁路旅客票价优化

程谦(南京铁道职业技术学院运输管理学院，江苏南京210031)*

基于不同目标的铁路旅客票价优化

程谦
(南京铁道职业技术学院运输管理学院，江苏南京210031)*

分析了铁路旅客运输市场结构，定义了铁路客票的价格函数.结合旅客出行行为方式选择模型，定义了铁路客运市场的需求函数并分析了铁路旅客运输的可变成本与边际成本.根据定价目标的不同，分别提出以运输企业盈利最大、以乘客需求最大、以社会福利最大的价格优化模型.在给定数据的简单网络上，对不同的定价模型进行数据检算，对比分析了不同定价目标的价格及收益，证实了模型的适用性.

交通运输经济;价格优化;非线性规划;铁路客运;价格函数;需求函数

0 引言

从经济学的观点出发，价格是运输市场中进行资源配置的有效工具.根据定价目标的不同，在充分的市场竞争条件下，优化的产品价格既可以保证运输组织者取得最大化的利益，也可以对市场中的客流进行有效调节.随着铁路旅客运输市场的不断发展、成熟，我国铁路企业针对旧有的“大一统”的价格管理模式正在逐步改革，有望实现更为灵活的、动态可调节的价格体系.

国内外的很多学者针对旅客运输票价优化这一课题进行了深入的研究.四兵锋在深入分析了铁路旅客运输市场供求关系的基础上应用城市道路网络平衡配流模型( UE)构建了双层规划模型来描述多种交通方式竞争条件下铁路旅客票价制定的最优策略［1］.陈建华在深入分析铁路旅客出行特点，以及旅客出行效用最大化的基础上，应用Logit模式分离模型描述旅客出行行为，并确定了最优票价［2］.张秀敏在车票折扣销售和存量控制方面应用最大凹向包络理论和EMSR票价动态控制方法解决了票价折扣销售和增加收益的问题［3］.国外的相关文献中，R.Borndorfer应用非线性优化模型构建了不同目标的公共交通优化模型，并应用实际数据测试了不同定价目标的定价差别［4］.Agostino应用离散选择模型模拟中长途铁路旅客运输中乘客的选择行为，应用实际数据对现行价格政策进行评价［5］.Van详细阐述了铁路旅客票价优化以及差别定价的经济学理论以及在荷兰国铁的应用，并针对不同时期的价格弹性差异提出了定价改进的建议［6］.上述文献大多是以运输企业收入最大化作为定价目标来进行价格优化的，但是由于铁路运输企业具有一定的社会属性，使得企业在进行价格决策时，并不完全以收入最大化作为唯一的定价目标.本文在前述研究的基础上，分析了我国铁路旅客运输产品的市场结构，定义了铁路运输产品的价格函数，并应用旅客出行行为选择模型( Logit)定义了需求函数.针对运输企业收入最大化、旅客需求最大化、社会福利最大化的不同优化目标条件，构建了相应的数学模型，并结合给定数据，验证了不同定价优化模型的适用性.

1 铁路旅客运输市场结构

1.1价格函数

根据《铁路客运运价规则》的规定，我国目前的铁路客运票价是由客票票价与附加票票价组成.基本票价以每人每公里的票价率为基础，加上按各种列车等级、空调、席别的上浮比率，以“递远递减”的方式计算.其中列车运行公里数以《铁路客运运价里程表》上公布的为准.硬座(含无座)为起始基准票价率，其他席别如硬卧、软座、软卧等均以此基准票价率上浮.影响铁路旅客票价的主要因素包含两部分，一部分为固定收费部分，另一部分为随运输距离远近而变化收费的部分，根据相应的票价率以及乘车里程，满足“递远递减”原则.这种结构关系可以利用图1来描述.可以看出图中有三段截距不同、斜率不同的直线分别代表不同旅行距离的价格.三段不同直线的不同截距表示价格的固定收费部分.不同的斜率代表着相应的票价率.随着旅行距离的不断增加，直线的斜率减少.

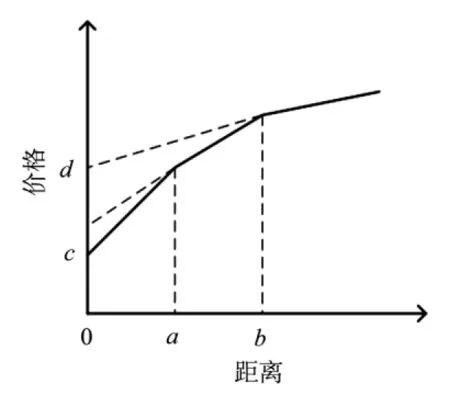
图1 铁路客票价格与旅行距离关系图

基于以上分析，不失一般性，提出如下价格函数

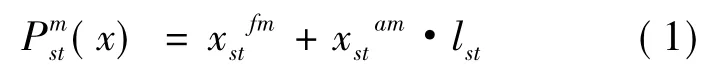
其中: st为OD对，始发s站终到t站，s，t∈D; m为服务产品，硬座，软座，硬卧等，为一个OD对间，m类客票的价格，其中x是2维向量;为m类客票固定收费价格;为m类客票票价率; lst为OD间距离.

1.2需求函数

在铁路旅客运输市场中与服务相对应的就是乘客的需求.准确测算一定时期内乘客对某一服务的需求对于价格优化的实现具有关键的作用.从经济学的观点来看，影响乘客需求的因素有很多，其中最主要的包括价格、舒适程度、正点率等.在相关研究中，需求函数大多是以历史数据结合上述因素经过回归分析得到的统计模型.但近年来，一些文献对需求函数的确定逐渐由预测模型转向研究个人对运输产品选择的选择行为模型.从旅客的出行特征来看，此类模型能较好地描述旅客的购买行为.

非集计Logit旅客出行行为选择模型是研究交通出行行为使用较广泛的模型之一.该模型反应了出行者旅客对服务的选择行为，出行者对服务选择的目标是建立在追求“效用”最大化的基础上.这里的“效用”是指与出行者自身相关的需求影响因素集合，包括价格、舒适度等.通常随机效用理论将效用函数U，分为非随机变化的部分V (固定项)和随机变化的部分ε(概率项)两部分，并假设它们两者间呈线性关系，如下式.

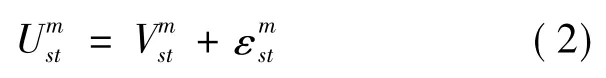
影响出行者购买行为的主要因素一般来说主要包括，车票价格、旅行时间、舒适程度.反映到效用函数中，参考文献［5］、［6］，可以采用线性模型来表示，如式( 3).

式中:β0，β1，β2为系数项;这里指不依赖车票价格、旅行时间等的固定效用常量;

指一个OD段内，m类产品的旅行舒适度水平.

为简化分析，如果仅以价格作为行为选择的影响因素，则出行者效用函数为.

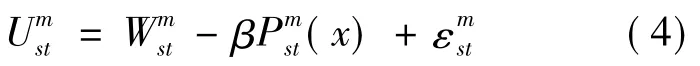
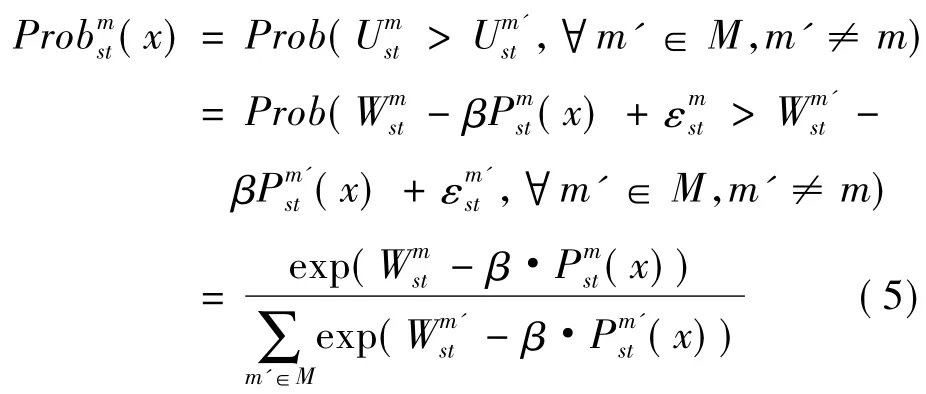
如果设定研究范围内铁路运输的总需求为Q，则相应的需求函数为:

1.3成本函数

根据经济学的定义，运输企业的成本就是企业为生产服务产品所消耗的代价.成本是进行收入优化的关键因素之一.一般来说，铁路运输企业的成本主要包含三类，固定成本、可变成本和沉没成本.轨道、桥梁等基础设施属于沉没成本.机车、车辆等大型设备属于固定成本.另外，根据企业生产水平而投入的人力、部分设备则属于可变成本.在短期范围内衡量运输企业收入的成本指标主要是指可变成本与边际成本.铁路运输中的边际成本是指每增加单位人/公里运输所产生的成本支出.由于铁路运输生产所涉及的生产要素繁多，因此在实际应用中很难准确掌握铁路运输生产的边际成本.一般通过利用模拟可变成本函数来计算边际成本.式( 7)为可变成本函数，式( 8)为边际成本函数.

上两式中q为一定时期内的产出水平; C与MC分别表示可变成本与边际成本.

在实际分析中边际成本并不是一成不变的.在运输能力紧张时期(如寒暑运)和运输能力富裕时期的边际成本变化较大.

2 价格优化模型

2.1企业盈利最大化为目标

企业盈利是企业收入与运营成本的差值.根据上述几节的分析，可以得到以企业盈利最大化为目标的价格优化模型，如式( 9)所示.

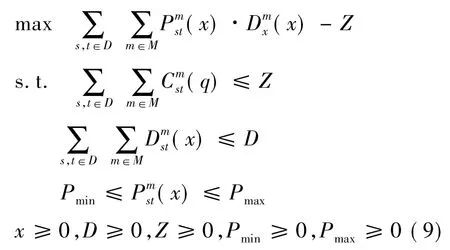
上式中，Z是可变成本的限界值.在计算中可以选择成本的常量数值代替，则相应约束条件可以取消而不影响计算结果.Pmin与Pmax是价格设定的上下限值，可以根据相应的价格政策要求选取.D是运输企业生产能力，运输需求D( x)应满足运输企业生产能力约束.其余符号说明与上节相同.

2.2需求最大化为目标

在保证基本经营成本的基础上，通过适当的定价使得市场需求达到最大，是铁路运输企业在不同经营时期需要考虑的目标.甚至在一些特定地区的特定线路上，铁路企业的社会属性要求要大于企业经营属性的要求.此时，以旅客需求最大化作为定价目标并辅以一定程度的政府补贴作为维持运输企业正常运营的价格调节手段.

以旅客需求最大化作为目标的价格优化模型为

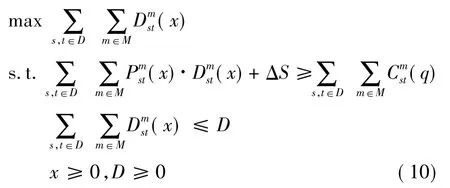
上式中，ΔS是政府补贴支持，企业盈利与政府补贴支持的和应不小于运营成本支出，这样才能保证运输企业维持正常经营.

2.3社会福利最大化为目标

铁路旅客运输作为国家综合交通体系之中重要的一种运输方式，在日常经营中要体现铁路企业的社会福利属性.根据经济学定义，社会福利是运输供给方与需求方的总剩余.运输生产部门所取得的剩余就是收入所得.运输需求方所取得的剩余是旅客在对服务产品购买时，支付意愿价格与实际支付价格的差值.在2.2节中曾经提出，旅客在对服务产品选择的过程中始终满足自身效用最大的选择方式.因此，可以利用效用函数(式( 3) )来描述旅客自身效用.

则相应的价格优化模型为

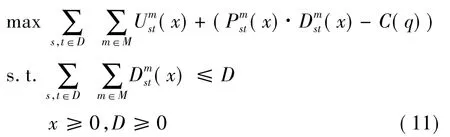
同上两式相同，在约束条件中，旅客对运输产品的需求应满足企业生产能力的限制.

不同的价格优化模型对应于不同的定价目标与定价主体.铁路运营企业作为铁路运输系统的主要参与方，其参与市场竞争的目的是实现利益最大化，因此，以企业盈利最大化为目标的定价模型反映了铁路企业的定价需求;出行者作为铁路旅客运输的服务对象，其出行需求应最大程度满足，以需求最大化为目标的定价模型在一定程度上反映了出行者的定价需要;政府部门作为铁路运输系统的监管方，以社会福利最大化作为定价目标更为适合.在实际应用中，应综合三个不同的定价模型的计算结果，综合考虑定价选择.

3 算例应用

3.1背景说明

为了验证在上节中提出的不同目标的价格优化模型，本文构建了包含三个节点的简单路网结构在单位时间(一日)内两类客票(一等座，二等座)的需求、价格设定、收益等数据变化情况.如图2所示.

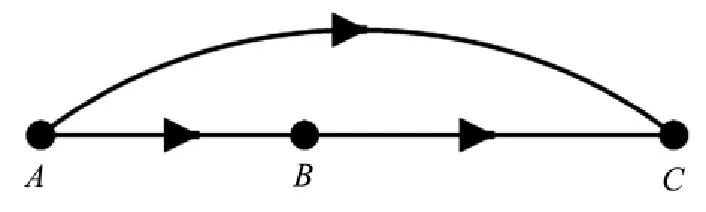
图2 网络示意图

需要说明的是，为简化计算此处给定为单向网络.图中站间距离lst由下式给出，单位为km.

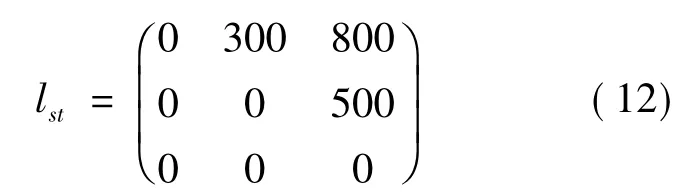
站间出行需求为，单位为万人.

其余有关参数选择如表1所示.其中，价格影响系数参考文献［2］取值.调价限值中最低价格根据相应里程普通旅客列车(绿皮车)票价确定，最高价格依据航空票价确定.

表1 相关参数取值表

3.2计算

上述价格优化模型均为非线性规划模型，模型的计算规模取决于实际应用路网规模，在本次研究中应用MATLAB 7.10优化软件对模型数据进行验证计算.表2给出了以收入最大化为目标的优化结果，表3给出了不同优化目标的价格差异.

表2 收入最大化的最优定价

表3 不同优化目标的价格比较

从数据计算结果来看，上述价格优化模型能够反映不同目标的定价需求，在应用到优化定价决策上是可行的.

4 结论

本篇论文对不同目标的铁路旅客车票优化方法进行了分析.论文提出了运输企业收入最大化、乘客需求最大化、社会福利最大化的不同目标的价格优化模型.在给定数据的简单网络上，通过计算分析，可以看出，价格作为乘客出行选择的重要影响因素之一，可以定量化的反映在对运输产品的需求上，应用非集计Logit出行行为选择模型构建需求函数，并应于目标定价，对于铁路运输企业定价决策是可行的.

应用不同定价目标合理制定产品价格的前提是对铁路客运市场需求、供给、以及成本的准确分析.本文提出的方法还有待今后在实际应用中加以验证.此外，文中所提出的定价模型均为单目标定价模型，并不能综合反映铁路旅客运输相关参与主体的利益诉求，多目标综合优化定价模型应作为后续研究方向.

［1］四兵锋，高自有.合理制定铁路客票价格的优化模型及算法［J］.管理科学学报，2001，4( 2) : 45-51.

［2］陈建华.铁路旅客票价优化问题的相关模型及算法［D］.北京:北京交通大学，2007.

［3］张秀敏.我国铁路客票折扣销售研究［D］.成都:西南交通大学，2002.

［4］BORNDORFER R.Models for fare planning in public transport［J］.Discrete applied mathematics，2012，160 ( 18) : 2591-2605.

［5］AGOSTINO NUZZOLO.A behavioral choice model for the evaluation of railway supply and pricing policies［J］.Transportation research Part A，2000，34( 5) : 395-404.

［6］VAN VUUREN D.Optimal pricing in railway passenger transport: theory and practice in the Netherlands［J］.Transport policy，2002，9( 2) : 95-106.

［7］陶媛.大城市停车换乘( P＆R)系统的实施条件及规划设计方法研究［D］.北京:北京交通大学，2008.

下期待发表文章摘要预报

Study of Optimal Pricing in Railway Passenger Transport based on Different Goal

CHENG Qian
( School of Transportation and Management，Nanjing Institute of Railway Technology，Nanjing 210031，China)

The structure of the market of railway passenger transportation is analyzed.In supply side，the ticket fare function is developed on the rules of China railway passenger ticket.In demand side，the demand function is proposed on discrete choice model，assuming maximal the utility of the passenger.The marginal cost and variable cost of the market is also studied.Three pricing models are provided based on various objects，and these optimal systems are computed using example data.

transportation economy; optimal tariffs; nonlinear programming; railway passenger transport; price function;demand function

A

1673-9590( 2016) 01-0006-05

2015-07-20

南京铁道职业技术学院基金资助项目( Y11015)

程谦( 1977－)，男，讲师，硕士，主要从事铁路运输规划与管理的研究

E-mail: 13851522967@139.com.

book=10,ebook=13