高速铁路桩承式路基土拱安定性分析
毕宗琦, 宫全美, 周顺华, 韩高孝
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
桩承式路基中土拱的稳定性直接关系到路基结构的服役性能。列车瞬时冲击荷载或长期循环荷载的作用均有可能导致拱效应的重新调整或失稳破坏,从而导致路基面较大的变形、道床板的开裂等,加大养护维修费用,甚至影响铁路正常使用。这一问题在变形控制要求极为严格的高速铁路无砟轨道路基结构中尤为突出。
目前有关桩承式路基中土拱效应的研究多数都是在静力条件下进行的[1-9],国内外学者对桩承式路基中土拱的形状、影响因素、荷载分担等开展了系统的探索。针对动荷载作用下桩承式路基中土拱效应发生退化失稳现象的相关研究近年来同样取得了一定的进展。肖宏[10]、叶阳升等[11]对桩网结构路基进行了现场动力测试试验,结果表明动荷载作用下土拱效应依然存在,但动荷载对路基不同深度处应力传递模式有一定的影响。Heitz等[12]进行了静-动荷载共同作用下1∶3室内模型试验研究,试验中土拱出现了退化现象(表现为桩土应力比减小),并据此提出了拱效应动力折减系数。Lai等[13]利用PFC2D研究了递增动荷载作用下桩承式路基中土拱效应的演变规律并将其分为逐步加强、形成-破坏-重构、失稳三个阶段。韩高孝、宫全美等[14-16]通过模型试验和离散元研究了动荷载作用下影响土拱稳定的因素及土拱退化和破坏的基本特征,同样得到了动荷载削弱土拱中荷载转移效果的结论,其认为动荷载作用下土拱效应的失稳退化是由拱顶、拱脚土体发生塑性破坏引起的,在退化过程中伴随着土体内部应力状态的调整,导致了土压力系数的变化以及主应力方向的偏转。
循环动荷载下土拱的稳定性的变化模式可分为瞬时破坏、渐变破坏和稳定三种[17],拱体所受动荷载大小超出瞬时-渐变破坏临界值时会导致主力链颗粒间形成的稳定摩擦结构在短时间内发生大变形而破坏,而大于渐变破坏-稳定状态临界值的荷载作用虽不足以在初始数个周期内产生破坏,但长期变形的累积最终将导致结构失稳。目前的研究仅限于对这一现象的定性发现,而对其机理性的认识、变化特性、影响因素等的研究尚未有合理的解答。循环动荷载作用下土拱何时发生退化或破坏则缺少明确的判别条件和相应的分析方法。
安定理论的提出始于20世纪30年代初,其主要研究结构在复杂加载条件下能否达到稳定状态,以及后续塑性行为的发展趋势。土拱的动力稳定特性同样可以借助安定理论进行解释,本文根据改进的Hewlett土拱模型,对循环荷载作用下拱脚区域进行安定性分析以确定其弹性状态、安定状态、破坏状态的临界荷载,从而给出动力作用引发土拱失稳不同阶段的界限值。
1 土拱破坏模式
在理想情况下,土拱形成后表现为仅受截面轴力作用的合理拱轴线形式,假定土拱区域内土体主要承受压力作用。桩间土以上路堤的自重以及表面的附加荷载,通过土拱传递于桩帽上,使桩帽上的竖向应力大于桩间土的竖向应力,同时假定土拱区域内部将因材料摩擦力的调动产生应力状态的改变。随荷载作用的增强,某些位置乃至整个土拱结构体中的土体可能生成塑性点或进入极限状态,使荷载转移的效果受到影响,即土拱发生了退化、失稳和破坏。
根据土拱的受力特点,拱顶及拱脚是最容易发生失稳破坏的位置[18]。根据Hewlett模型[1],土拱的塑性点可能出现在土拱顶部的中心点或是桩帽上方的土拱拱脚处。在拱顶中心位置,外部荷载垂直于拱轴线,在垂向荷载幅值过大时易发生剪切破坏,通常以极限平衡条件作为其强度标准;在拱脚处的土体则主要承担压力作用以及相邻土拱间的作用力,易受到挤压而产生塑性破坏[19]。其中,拱顶位置的剪切破坏主要受桩间净距的控制,若桩间距及填筑高度设置不合理,土拱在形成过程中可能发生坍塌失稳;而拱脚位置的破坏很大程度上归因于过大的附加荷载作用,同时桩帽的宽度对拱脚稳定性也有一定的影响。本文针对土拱以上破坏模式,对拱顶、拱脚的受力状态进行分析。
2 循环荷载作用下土拱受力分析
在循环荷载作用下,土拱效应的削弱具体表现为桩土应力的重新分布以及土体内部主应力方向的偏转,使桩间土承担更多的填土荷载而桩体承担的填土荷载有所减小。假定土拱结构体为理想弹塑性材料,基于Mohr-Coulomb屈服准则,忽略时间相关因素(速度敏感性、蠕变等),考虑循环荷载作用为准静态过程,分析自重及循环荷载作用于桩间土及桩帽上方的应力大小。
根据球形土拱顶部单元体的竖向受力平衡条件(图1)可得
( 1 )
( 2 )
式中:γ为路基材料重度;Kp= (1+sinφ)/(1-sinφ)为朗肯被动土压力系数,φ为内摩擦角;c为材料黏聚力。


σsg=
( 3 )
式中:s为桩中心距;d为桩帽宽度;H为桩顶至路基顶面深度。

附加循环荷载作用于拱顶的应力σa则考虑其幅值沿深度的衰减效应,结合路基中实测动应力衰减规律,采用拟静力方法据Boussinesq解求得
( 4 )
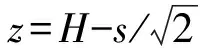

( 5 )
进而求解出作用于桩间土上的附加动应力为
( 6 )

将式( 3 )、式( 6 )求得的自重应力与附加动应力叠加,得作用于桩间土上的垂向应力σs,并考虑应力分布的非均匀性[2],见图2,利用不均匀系数η进行修正,即
σsu(λ)=ησs(λ)=ησsg+σsa(λ)
( 7 )
作用于桩帽上的垂向应力σp(λ)=σpg+σpa(λ)可根据整体竖向受力平衡条件求得。其中,自重及循环荷载引起的应力分别为
( 8 )
式中:σd1、σd2分别为在深度z=H处根据式( 4 )求得的角点、中点应力值,与λ有关。
3 土拱安定性分析

3.1 塑性区发展分析与弹性、破坏荷载临界值
结合目前针对桩承式路基土拱效应的相关模型试验及数值研究中给出的规律[13, 24-25],对桩帽顶部即土拱拱脚处进行分析。拱脚附近土体的主应力方向发生偏转并集中指向桩顶,且靠近桩顶边缘的主应力方向偏转程度更大;相对于桩帽中心位置,边缘处应力水平和材料强度发挥程度更高从而更易产生屈服;破坏时拱脚区域受到较大的压缩。本文在此基础上构造一弹塑性应力场,假定屈服首先由桩顶边缘即拱脚内边界产生,塑性区逐步向桩中心位置发展。认为当拱脚边界位置刚达到屈服时为弹性临界状态,此时的外荷载pe为土拱的弹性极限荷载,大于该值的循环荷载将使拱脚产生一定的塑性变形;随荷载幅值增大,在少量的几个循环内拱脚全断面将达到塑性极限状态即土拱发生破坏,此时的外荷载pp为土拱的临界破坏荷载。

如图3所示,取土拱区内、外边界的土体单元进行分析,设作用于拱脚位置内、外边界的径向压力分别为σib、σob,根据实际主应力分布情况,拱脚内侧临近桩间土位置的土压力系数大于1,处于被动土压力状态,而桩帽上方区域则处于主动土压力状态。根据对应位置单元体所受竖向应力可求得拱脚的内、外侧边界条件为
( 9 )
式中:Ka为主动土压力系数。
分析土拱在内外两侧压力共同作用下的弹塑性应力响应。将拱脚单元近似视为平面应变状态的理想弹塑性体,当荷载幅值较小时表现为纯弹性响应,据Lame解答,径向、环向应力分量分别为
(10)

(11)
式中:λe为土拱的弹性荷载乘子临界值。由此即可得到弹性极限荷载pe,即pe=λep0。
在作用荷载大于弹性极限荷载后,拱脚进入部分屈服的弹塑性状态。当λ>λe时,拱脚位置将形成塑性区。如图4所示,假设塑性区与弹性区的交界面的径向坐标为rp,即拱脚处沿径向塑性区的分布为R1≤r≤rp,弹性区为rp (12) (13) 设弹塑性交界面的应力边界条件为σrr=rp=q,可求得塑性、弹性区应力为 R1≤r≤rp (14) rp (15) 未知项q可根据拱脚内侧应力边界条件σrr=R1=σib(λ)解得 (16) 式(15)应在r=rp处满足屈服条件,据此求得荷载乘子λ与交界面坐标的关系函数P(λ)为 (17) 当给定一个外载荷时,其相应的rp也随之确定。随λ的增大,当塑性区发展至rp=R2=s/2时弹性区消失,拱脚达到塑性极限状态,有 (18) 式中:λp为临界破坏荷载乘子,进而可确定使土拱发生失稳破坏的临界荷载pp=λpp0。 当载荷乘子满足λe≤λ≤λp时,拱脚位于弹塑性状态。初始正向加载时会产生一定的塑性变形,这一部分变形导致反向卸载后形成一残余应力场ρij,若在后续加卸载中此残余应力场保持恒定,且与不超出λ控制范围的外荷载作用叠加后仍处处满足屈服条件,则结构将呈安定状态。根据最佳残余应力场的构造方法,完全卸载后结构保持稳定的充要条件是ρij自身不发生反向屈服,从而卸载过程的应力响应为纯弹性,并在后续循环中不产生新的塑性变形累积。根据已知弹塑性状态的拱脚处的总应力场分布,构造满足条件的最佳残余应力场并寻找荷载乘子的极大值,可得到拱脚的临界安定荷载psd。 塑性区R1≤r≤rp (19) 弹性区rp (20) 土拱的安定性分析则转化为沿拱脚径向上的一维搜索最优化问题,即 λsd=maxλ s.t. maxf(ρij)≤0 ρij=F(λ,r) λe≤λ≤λpR1≤r≤R2 (21) 求解式(21)即可得到安定荷载乘子λsd的值。当荷载幅值大于临界安定荷载psd=λsdp0时,土拱将因每个循环中不断累积的塑性变形而导致在一定荷载作用次数后发生失稳破坏。 文献[17]针对动荷载作用下高速铁路桩承式路基的土拱稳定性进行了相关室内模型试验。试验以京沪高铁某断面桩-网结构路基为原型,该断面地基采用CFG桩处理,桩间距1.8 m,桩帽宽度1.0 m,填筑高度约2 m。模型中各结构尺寸按几何相似比CL=1∶6.5进行设置,见图6、图7。试验在边长为55 cm,高为100 cm的有机玻璃模型箱中进行,共设置4根混凝土桩,桩帽宽d=15.3 cm,桩中心间距s=27.5 cm,净距s1=12.2 cm。试验中路基填土材料选用含水率为3%的砂土,其颗粒级配不均匀系数Cu=3.33,曲率系数Cc=0.97,内摩擦角为φ=31°(直剪试验所得)。模型中填土高度H=30 cm,填筑后容重约为γ=14 kN/m3。激振器放置在一边长为40 cm的加载板上,提供振动频率30 Hz、最大幅值p0=20 kPa的半正弦型动荷载,共进行循环加载18万次,以模拟高速铁路路基中的列车动应力。桩帽、桩间土上方按5 cm竖向间距布置DYB-1型电阻应变式土压力传感器,数据通过DH-5922动态信号测试分析系统采集处理。 试验研究了动荷载幅值变化对桩土应力比的影响,并反映土拱的退化、失稳以及破坏状态。当加载后桩土应力最终趋于相同即σp/σs= 1时认为路基中荷载分配传递的能力已经丧失,土拱发生失稳破坏;当加载后σp/σs位于1~1.2时认为土拱达到临近破坏阶段;当σp/σs大于1.2时认为土拱效应仍能保持长期的稳定。如表1所示,在动应力幅值为10、13、17 kPa时,加载后的桩土应力比均较填筑自重作用下减小,且荷载幅值越大衰减越显著,这说明土拱效应下桩的荷载分担效果受到了削弱。试验1~3中的土拱在加载后分别处于安定、临近破坏及失稳破坏状态,并据此判断该试验中土拱安定荷载的临界值在13 kPa附近。 表1 施加动荷载前后桩土应力比 利用本文的计算方法分析该模型中的土拱效应。根据以上试验参数设置计算条件,取泊松比μ= 0.3,忽略砂土黏聚力,桩间土应力不均匀系数η= 0.8[26]。首先考虑自重荷载作用,由式( 7 )、式( 8 )计算作用于桩帽及桩间土上的应力,得填筑时桩土应力比为3.50,与实测值3.11近似。循环加载时,通过式(21)计算得安定荷载乘子λsd= 0.62,即安定荷载为psd=p0×λsd= 12.39 kPa。当外荷载作用大于该值时,将导致在循环中发生塑性变形的持续累积,直至破坏,这与试验规律基本相符。 上述计算方法在确定弹性、安定、破坏荷载乘子临界值时,考虑了材料内摩擦角φ、桩间距s、桩帽宽度d及填土高度H的影响。改变计算参数分析临界荷载乘子λe、λsd、λp随之变化的规律,计算结果见图8~图11。 如图8所示,随内摩擦角即土体抗剪强度的提高,3个荷载乘子临界值均有明显的增加。临界破坏荷载始终大于安定临界荷载以及弹性极限荷载,在摩擦角较小时安定荷载接近弹性极限荷载,说明在抗剪强度不足时土拱结构难以达到安定状态。 在摩擦角φ=31°时,研究桩间距s变化对荷载乘子临界值的影响,如图9所示。可以看出,增大桩间距将使临界破坏荷载、安定荷载与弹性极限荷载有所减小,说明较小的桩间距有利于土拱在外荷载作用下的稳定性。 如图10所示,增加桩帽宽度将扩大拱脚承载面积,显著提高荷载分担能力,使临界破坏荷载迅速增加,同时安定荷载与弹性极限荷载上升平缓,后续呈现一定的收敛趋势。当桩帽宽度较小时弹性、安定荷载阈值小于0,表明在此条件下拱脚无法避免循环荷载作用导致的塑性变形的产生和累积。 如图11所示,填土高度的增加对荷载临界值造成两方面影响:(1)附加荷载将沿深度衰减,对土拱区域影响逐渐减小;(2)覆土重量的增加将导致拱脚处应力的增大。计算结果表现为随填土高度增加,临界破坏荷载增大而弹性荷载略有减小,安定荷载则呈现先增大后减小的趋势但变化不明显,荷载乘子最大值位于H=32 cm处。 本文以桩承式路基中桩帽上方的土拱拱脚位置作为研究对象进行安定性分析,求解了土拱稳定-失稳破坏状态间的弹性、安定、破坏荷载临界值,得出以下结论: (1) 考虑循环荷载对土拱效应的影响,改进了Hewlett土拱分析方法,可分析循环荷载引起的附加应力及其沿深度的衰减,计算得到的桩土应力比与试验结果相近。 (2) 基于Mohr-Coulomb屈服准则对拱脚处在循环荷载作用下的弹塑性行为进行分析,拱脚处于弹性状态时无塑性区产生,发生破坏时则全断面进入塑性状态,塑性区边界随循环荷载幅值增大而扩张。据此给出了土拱弹性极限荷载与临界破坏荷载的求解方法。 (3) 通过构造最佳残余应力场的方法进行了安定性分析,经过最优化搜索,求解了反映土拱稳定特性的安定荷载。根据模型试验参数,对于填筑高度/桩间净距约为2.5,路基材料为砂性土的高速铁路桩承式路基,计算确定的安定荷载临界值为12.39 kPa,与试验中土拱发展、破坏规律较为符合。 (4) 根据计算结果,弹性极限荷载、安定荷载、临界破坏荷载随材料内摩擦角的增大、桩间距的减小、桩帽宽度的增加而增大,填土高度的增大会减小弹性荷载临界值并增大破坏荷载临界值,而安定荷载则变化不明显。临界破坏荷载始终大于安定荷载及弹性荷载,且受到以上因素变化的影响较后者更为显著。 (5) 安定荷载临界值可作为长期循环荷载作用下土拱稳定与否的量化判据之一,其对高速铁路桩承式路基结构设计具有一定理论意义。 参考文献: [1] HEWLETT W J, RANDOLPH M F. Analysis of Piled Embankments[J]. Ground Engineering, 1988, 21(3):12-18. [2] LOW B K, TANG S K,CHOA V. Arching in Piled Embankments[J]. ASCE Journal of Geotechnical Engineering, 1994, 120(11): 1 917-1 938. [3] 陈云敏, 贾宁, 陈仁朋. 桩承式路堤土拱效应分析[J]. 中国公路学报, 2004, 17(4): 1-6. CHEN Yunmin, JIA Ning, CHEN Renpeng. Soil Arch Analysis of Pile-supported Embankments[J]. China Journal of Highway and Transport, 2004, 17(4): 1-6. [4] KEMPFERT H G, GOEBEL C, ALEXIEW D, et al. German Recommendations for Reinforced Embankments on Pile-similar Elements[C]// Third European Geosynthetics Conference, Geotechnical Engineering with Geosynthetics. Munich: German Geotechnical Society, 2004: 279-285. [5] ROGBECK Y, GUSTAVSSON S, SÖDERGREN I, et al. Reinforced Piled Embankments in Sweden-design Aspects[C]// Proceedings of the 6th International Conference on Geosynthetics. Atlanta, United States:Industrial Association International,1998:755-762. [6] VAN EEKELEN S J M, BEZUIJEN A, VAN TOL A F. Analysis and Modication of the British Standard BS8006 for the Design of Piled Embankments[J]. Geotextiles and Geomembranes, 2011, 29(3): 345-359. [7] ELLIS E A, ASLAM R. Arching in Piled Embankments: Comparison of Centrifuge Tests and Predictive Methods-Part 1 of 2[J]. Ground Engineering, 2009, 42(6): 34-38. [8] ELLIS E A, ASLAM R. Arching in Piled Embankments: Comparison of Centrifuge Tests and Predictive Methods-Part 2 of 2[J]. Ground Engineering, 2009, 42(7): 28-31. [9] NAUGHTON P J. The Significance of Critical Height in the Design of Piled Embankments[C]//Geo-Denver Conference: New Peaks in Geotechnics, ASCE Geotechnical Special Publication (GSP) No. 172 - Soil Improvement. Denver, Colorado, United States:America Society of Civil Engineers,2007:1-10. [10] 肖宏, 蒋关鲁, 魏永幸. 遂渝线无砟轨道桩网结构路基现场动车实验测试分析[J]. 铁道学报, 2010, 32(1): 79-84. XIAO Hong, JIANG Guanlu, WEI Yongxing. Dynamic Test Analysis on Ballastless-track Column-net Structure Subgrade of the Suining-Chongqing Railway Line[J]. Journal of China Railway Society, 2010, 32(1): 79-84. [11] 叶阳升, 张千里, 蔡德钩, 等. 高速铁路桩网复合地基低矮路基动静荷载传递特性研究[J]. 高速铁路技术, 2010, 1(1): 10-15. YE Yangsheng, ZHANG Qianli, CAI Degou, et al. On Static and Dynamic Load Transfer Peculiarity of Low Embankment for High Speed Railway Pile-net Composite Foundation[J]. High Speed Railway Technology, 2010, 1(1): 10-15. [12] HEITZ C, LVKING J, KEMPFERT H G. Geosynthetic Reinforced and Pile Supported Embankments under Static and Cyclic Loading[C]// Proceedings of the 4th European Geosynthetics Conference. Edinburgh, UK:International Geosynthetics Society,2008: 215. [13] LAI H, ZHENG J, ZHANG J, et al. DEM Analysis of “Soil”-arching within Geogrid-reinforced and Unreinforced Pile-supported Embankments[J]. Computers and Geotechnics, 2014, 61: 13-23. [14] HAN Gaoxiao, GONG Quanmei, ZHOU Shunhua. Mechanical Analysis of Soil Arching under Dynamic Loads[C]// 14thPan-American Conference on Soil Mechanics and Geotechnical Engineering. Toronto, Canada: Canadian Geotechnical Society,2011. [15] HAN Gaoxiao, GONG Quanmei, ZHOU Shunhua. An Experimental Investigation of Soil Arching under Dynamic Loads[C]// 11thInternational Conference of Chinese Transportation Professionals. Nanjing, China:America Society of Civil Engineers,2011:3 030-3 037. [16] 韩高孝, 宫全美, 周顺华. 列车动荷载下桩网结构路基土拱效应试验研究[J]. 岩土力学, 2014, 35(6):1 600-1 606. HAN Gaoxiao, GONG Quanmei, ZHOU Shunhua. Experimental Study of Soil Arching Effect in Geogrid Reinforced Pile Supported Embankment under Train Dynamic Load[J]. Rock and Soil Mechanics, 2014, 35(6): 1 600-1 606. [17] 韩高孝. 列车动荷载作用下桩网结构路基土拱效应稳定性研究[D].上海:同济大学, 2015. [18] 周德培,肖世国,夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132-135. ZHOU Depei, XIAO Shiguo, XIA Xiong. Discussion on Rational Spacing between Adjacent Anti-slide Piles in some Cutting Slope Projects[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 132-135. [19] 杨明,姚令侃,王广军. 桩间土拱效应离心模型试验及数值模拟研究[J]. 岩土力学, 2008, 29(3): 817-822. YANG Ming, YAO Lingkan, WANG Guangjun. Study of Centrifuge Model Tests and Numerical Simulation on Soil Arching in Space of Piles[J]. Rock and Soil Mechanics, 2008, 29(3): 817-822. [20] MELAN E. Theorie Statisch Unbestimmter Tragwerke aus Idealplastischem Baustoff[R]. Sitzungsbericht der Akademie der Wissenschaften (Wien) Abt, ⅡA,1938,(195):145-195. [21] 陈钢, 杨璞, 刘应华. 弹塑性结构安定性上限分析的数值方法及应用[J]. 工程力学, 2005, 22(1):21-27. CHEN Gang, YANG Pu, LIU Yinghua. A Computational Approach to Kinematic Shakedown Analysis of Elastic-plastic Structures and Its Applications[J]. Engineering Mechanics, 2005, 22(1): 21-27. [22] 张明焕,杨海元. 结构安定分析方法研究[J]. 应用力学学报, 1994, 11(4): 83-90. ZHANG Minghuan, YANG Haiyuan. Study of Shakedown Analysis of Structure[J]. Chinese Journal of Applied Mechanics, 1994, 11(4): 83-90. [23] 王飞,栾茂田,朱菊芬,等. 基于弹塑性有限元分析土工安定性计算方法及其应用[J]. 大连理工大学学报, 2001, 41(3): 349-354. WANG Fei, LUAN Maotian, ZHU Jufen, et al. Shakedown Analysis of Soil Structures Based on Elasto-plastic FEM[J]. Journal of Dalian University of Technology, 2001, 41(3): 349-354. [24] 费康,王军军,陈毅. 桩承式路堤土拱效应的试验和数值研究[J]. 岩土力学, 2011, 32(7):1 975-1 983. FEI Kang, WANG Junjun, CHEN Yi. Experimental and Numerical Studies of Soil Arching in Piled Embankment[J]. Rock and Soil Mechanics, 2011, 32(7):1 975-1 983. [25] 韩高孝,宫全美,周顺华. 桩网结构路基土拱效应离散元研究[J]. 石家庄铁道大学学报:自然科学版, 2014, 27(4): 19-23, 36. HAN Gaoxiao, GONG Quanmei, ZHOU Shunhua. Research on Soil Arching Discrete Element of Pile Supported Geosynthetic-reinforced Embankment[J]. Journal of Shijiazhuang Tiedao University:Natural Science, 2014, 27(4): 19-23, 36. [26] 郭帅杰,宋绪国,罗强,等. 基于Hewlett方法的桩网复合地基土拱效应优化算法[J]. 铁道标准设计, 2015, 59(5): 16-23. GUO Shuaijie, SONG Xuguo, LUO Qiang, et al. The Improved Hewlett Method for Soil Arching Effect of Pile-net Foundations[J]. Railway Standard Design, 2015, 59(5): 16-23.

3.2 残余应力场的构造与安定荷载临界值

3.3 试验验证



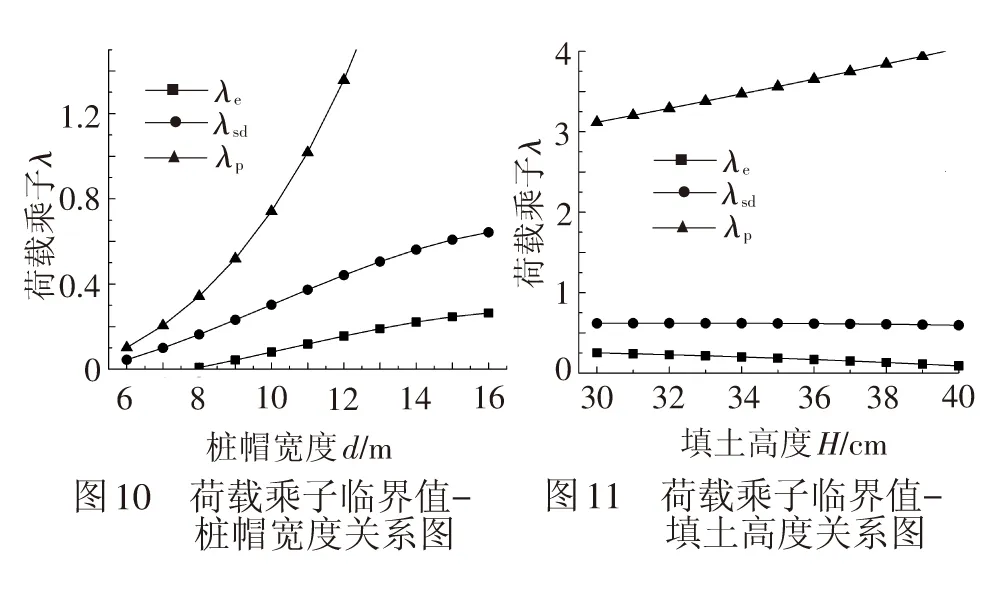
4 影响因素分析

5 结论

