采用交叉熵支持向量机和模糊积分的电网故障诊断

边莉，边晨源(黑龙江科技大学电子与信息工程学院，黑龙江哈尔滨150022)



采用交叉熵支持向量机和模糊积分的电网故障诊断

边莉，边晨源
(黑龙江科技大学电子与信息工程学院，黑龙江哈尔滨150022)

摘要:为了解决分布式电网故障诊断中局部电网内部故障和相邻区域联络线故障的诊断问题，采用交叉熵支持向量机(cross entropy support vectormachine，CE-SVM)的改进方法，提出一种基于后验概率输出的CE-SVM和模糊积分动态融合的大电网故障诊断策略。首先通过网络分区算法将电网分割成连通且计算负担平衡的子区域;采用历史数据离线训练各局部CE-SVM模块，根据故障报警信息选择性触发局部CE-SVM实现局部电网内部的故障诊断;利用模糊密度动态调节算法构建模糊积分环节，关联融合相连区域CE-SVM模块关于联络线故障的后验概率输出，实现联络线故障的综合决策。该方法不仅可以应对局部网络内部的故障诊断，也可以有效处理相邻区域间联络线的故障诊断问题。仿真结果看出:所得到的诊断结论正确，并且对于处理保护器和断路器报警信息丢失或不正确动作的情况具有较好的容错性。

关键词:分布式;大电网;故障诊断;交叉熵;支持向量机;模糊积分

边晨源(1989—)，男，硕士研究生，研究方向为电网智能故障诊断技术。

0　引言

随着电网规模的扩大、设备的增多，故障诊断的难度逐渐加大。国内外专家学者提出一系列电网故障诊断的方法和思路，主要有专家系统［1］，人工神经网络［2］和Petri［3］网等。不过要实现在线快速准确的故障诊断仍然是一个难题，尤其是当保护器和断路器存在不正常动作或报警信息缺失以及多重故障的情况下，在线故障诊断更为困难。支持向量机是在统计学习理论基础上发展起来的一种全新的机器学习算法，着重研究在小样本条件下的统计学习规律，有较强的泛化能力，目前已有很多研究将其应用于故障诊断领域［4－5］。不过支持向量机在应用中存在参数选取的盲目性问题，本文采用一种交叉熵支持向量机(cross entropy support vector machine，CE-SVM)的改进方法，即利用交叉熵优化算法对支持向量机参数寻优，来提升支持向量机的推广泛化能力。

基于分布式的思想来实现电网故障诊断，首先需要利用网络分区算法将整个电网划分为若干小规模的网络区域，各个子区域独立并行完成各自的诊断任务，从而提升诊断效率。不过要实现分布式的故障诊断需要解决3个主要问题:1)如何将大规模电力网络分割成一定数目的便于进行分布式故障诊断的局部电网;2)局部电网内部的故障诊断问题; 3)连接相邻2个子网络的联络线故障诊断问题。对于问题1)，采用文献［6］的方法可以较好的解决，本文的研究重点是问题2)和问题3)。离线阶段，针对每个局部电网，利用历史数据样本作为训练集，采用交叉熵算法改善支持向量机的参数寻优方式，构造各区域CE-SVM故障诊断模型，根据报警信息选择性触发相应区域的CE-SVM模块，各诊断模块并行完成各自诊断任务，实现局部网络内部故障的有效诊断，从而解决问题2);而对于问题3)，当局部电网间联络线故障时，若故障联络线的主保护和近后备保护未能隔离故障，而由远后备保护动作切除故障时，电网故障区域会蔓延扩大至邻近网络，而局部CE-SVM在没有相邻的对侧局部电网保护器和断路器开关状态信息的情况下，是无法准确判别故障元件的。为了解决此问题，本文在相邻局部网络间建立模糊积分环节，并采用一种网络重叠分区的思路［7］，将相邻局部电网间的联络线作为重叠区域分别归于这两个局部电网，当两两相邻的CE-SVM诊断模块被报警信息触发时，区域间的模糊积分环节得以触发，采用模糊积分关联融合相邻区域CESVM模块关于联络线故障的后验概率输出，完成先验信息与后验概率有机融合，实现联络线故障诊断综合决策。

本文方法在算例电网中进行了仿真测试，结果表明基于CE-SVM与模糊积分融合的大电网故障诊断方法诊断过程透明，易于构造和实现，能有效解决电网分区后局部网络内部故障诊断问题和相邻区域间联络线的故障诊断问题，对于各种复杂故障情况，诊断正确率高，具有良好的容错能力。

1　交叉熵支持向量机

1.1支持向量机原理

支持向量机(support vectormachine，SVM)基本思想是:对于线性不可分的样本，通过非线性映射φ(·)将欧式空间Rn中的输入数据T映射到高维特征空间(Hilbert空间)，从而转化为Hilbert空间上的线性可分问题，如式(1)。在Hilbert空间，通过构造最优分类超平面W(φ(T))确定分类决策函数y=sgn［W (φ(T))］，其中最优分类超平面参数的确定是依据结构风险最小化原则，通过引入拉格朗日乘子，构造与原始分类问题对偶的非线性规划问题并求解得到的［8］。

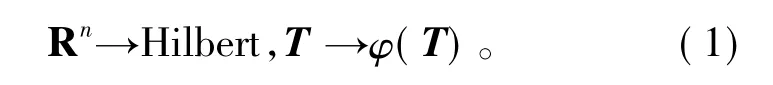
分类决策函数y的计算过程只涉及高维特征空间中输入向量与支持向量的内积运算，在非线性映射满足Mercer条件时，可利用核函数代替此内积运算。文献［4］通过实验证明采用径向基核函数和多层感知器核函数时，SVM的分类效果相当，并且均优于采用线性核函数和二次核函数时的分类效果。考虑到后续交叉熵算法优化核函数参数的复杂度，本文采用径向基核函数，有

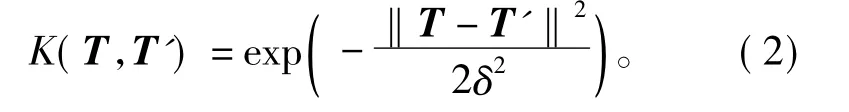
式中:‖T－T'‖为向量间距;δ为径向基宽度，用来描述高维特征空间的精确结构。

SVM的训练过程对参数的选取非常敏感，参数选取恰当与否将直接决定最终诊断模型的准确度，因此为了协调SVM的各个参数，提升SVM性能，采用一种交叉熵支持向量机(cross entropy SVM，CESVM)的改进方法，即利用交叉熵全局随机优化算法，对SVM中的2个主要训练参数:惩罚因子C和径向基宽度δ进行寻优。其中，径向基宽度δ控制与SVM对应的非线性规划问题最优解的复杂度，δ值太大或太小均会降低SVM的泛化能力;惩罚因子C取值太大或太小均易产生过学习或欠学习现象。

1.2交叉熵算法基本原理及优化流程

交叉熵(cross entropy，CE)算法的一个迭代的过程有两个步骤［9］:1)基于某一特定的概率密度函数，产生一组随机数据样本;2)依据这些数据样本更新概率密度函数的参数，从而为下次迭代贡献更优化的样本。在优化过程中，CE算法的操作基于参数化的概率密度分布，每次迭代使用的候选样本都发生变化［10］。考虑式(3)所示的无约束连续型优化问题，χ是一个表示状态的有限集，G是以χ为定义域的实值函数，其中γ*为G的最小值，x*为最优解。

设在χ上的一个概率密度函数族为{f(·;υ)，υ∈V}。对于一个给定的概率密度{f(·;η)，η∈V}，将式(3)的优化问题与式(4)的估计问题关联，研究G(X)比给定实数γ小的概率问题。

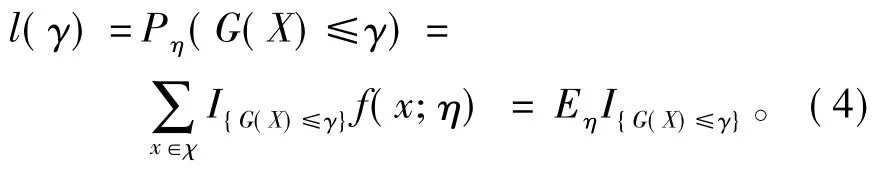
其中{I{G(X)≤γ}}表示指示函数集合，X是依据概率密度f(·;η)产生的随机样本，Eη表示相应的期望值。当γ逐渐接近γ*时，G(X)≤γ为小概率事件，但所选定的η，要保证Pη(G(X)≤γ)的值不是太小，因此式(4)中γ和η的选取是紧密相关的［10］。多级别算法能够解决目标事件概率过小所带来的限制，即构造参考参数序列{υt，t≥0}和级别序列{γt，t≥0}，然后υt和γt同时更新迭代。其中γt的更新值为在给定参数υt－1下，G(·)的(1－ρ)分位点(ρ取值不可太小)。本文以惩罚因子C和径向基宽度δ作为CE算法优化目标，算法中采样概率密度函数选择高斯分布N(μ，σ2)，适应度函数为SVM交叉验证概率，计算流程如算法1所示。

算法1:交叉熵算法优化SVM参数流程

1)开始:初始化参数向量μ0，，随机样本个数M，分位数系数ρ0，平滑常数β，n(μ0的维数)，令迭代次数t=0。

3)排序:计算每个样本对应的适应度函数值(本文取交叉验证概率)，并得到适应度函数值序列E=［E1，E2，…，EM］T;将该序列中的元素从小到大排列1≤2≤…≤M，得到新的矩阵序列，按照式(5)计算序列的(1－ρ0)分位数。

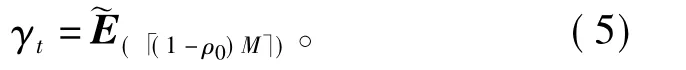
4)更新:利用产生的M个随机样本代入式(6)、式(7)，更新μ=(μ1，μ2，…，μn)和。令L=1，…，n。

5)平滑:

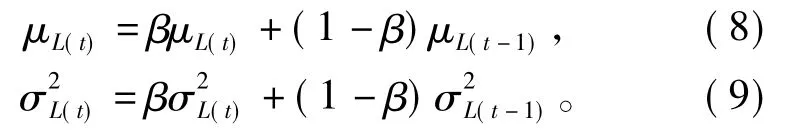
算法终止时，输出最优解X*=μ(t)，为一个2维向量，其中元素即为最优化的SVM参数C和δ。

2　后验概率输出算法

SVM在模式识别中，只考虑两种极端情况，属于某一类为1，不属于某一类为－1，无法得到预测样本的后验概率，而后验概率信息对于分类器的设计往往十分重要。Platt提出的后验概率SVM具有良好的概率输出功能［11］，但此方法仅能处理二分类问题。本文基于Platt模型构建具有多类别输出的SVM。

根据“一对一”方法训练SVM，给定“一对一”中每一个两类问题(u≠v)的训练样本数为nuv。SVM后验概率输出算法如下所示。

算法2:后验概率输出算法

1)采用Platt模型计算每一个两类问题的概率输出模型ruv=P(u|u or v)，如式(10)所示。

其中f是已知训练样本的决策值，Q和D是通过最小化训练样本的负对数似然函数估计出的［11］。

对于任意样本，利用全部ruv计算K类(K＞2) SVM的后验概率时，需满足条件

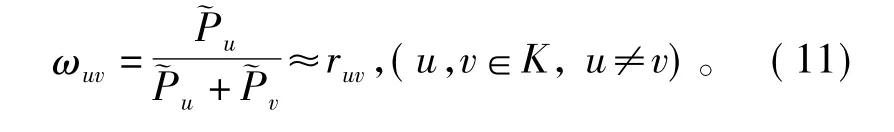
2)采用逐对耦合思想，使用Kubllback-Leibler距离来衡量ωuv与ruv的接近程度［12－13］，将式(11)转化为最大值问题，相当于找到一个使式(12)成立;随机初始化，计算相应的ωuv。

3)重复如下过程直至收敛，其中u=1，2，…，K，1，2，…，K，…循环。

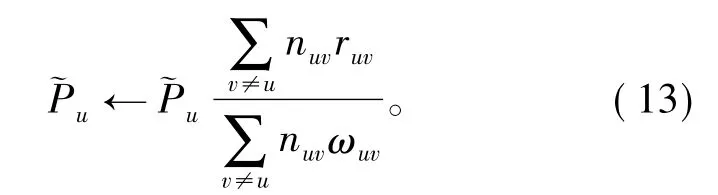
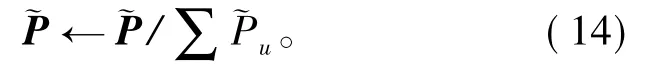
3　Choquet模糊积分融合

相比于常用的数据融合算法，如贝叶斯网络、D－S证据理论［14－15］，模糊积分不需要假设每个信源相互独立，能够评价不具有独立性的元素间具有的交互影响特性，可以有效地处理不确定性问题［14－16］。

3.1模糊测度

设Z={z1，z2，…，zn}为一有限集合，P(Z)为Z的幂集，定义在P(Z)上的集合函数g:P(Z)→［0，1］若满足正则性、单调性、连续性［16］，则称g为模糊测度。如果模糊测度还满足对∀A，B⊂Z，A∩B=φ，都存在λ＞－1，使得式(15)成立，则称该模糊测度为gλ－模糊测度。gλ－利用参数λ描述可加程度，是一种受λ值限制的模糊测度，目前应用最为广泛(以下g均表示gλ－模糊测度)。

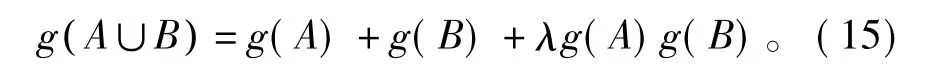
定义单点集上:gi=g({zi})，i=1，2，…，n，gi称为第i个信源的模糊密度，若已知各个信源的模糊密度值，可推导得出λ的计算公式为

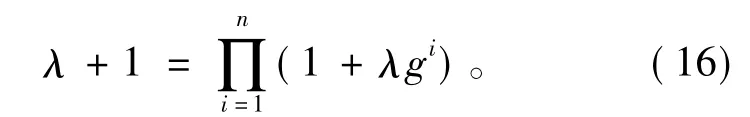
由式(16)可唯一确定λ，其中λ＞－1，且λ≠0。

3.2 Choquet模糊积分

模糊积分是定义在模糊测度上的一种线性函数，常用的模糊积分是Murofushi和Sugeno提出的Choquet积分［17］。对于有限集合Z={z1，z2，…，zn}，函数h:Z→［0，1］，则h在Z上关于模糊测度g 的Choquet模糊积分定义为

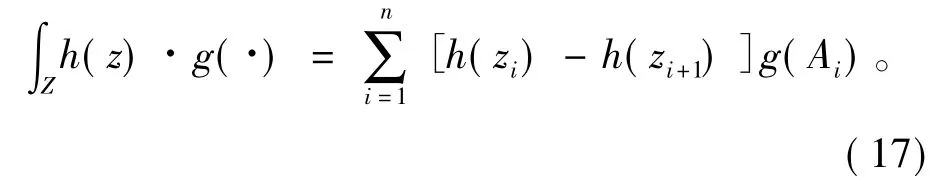
式中:函数值h(·)按照降序排列，即h(z1)≥h(z2)≥…≥h(zn)。Choquet积分可视为函数h(zi)的加权和。

函数h(zi)(i=1，2，…，n)可视为信源zi的可信度。Ai={z1，z2，…，zi}为论域里的子集，模糊测度g(Ai)可通过式(18)的递归形式求解，有

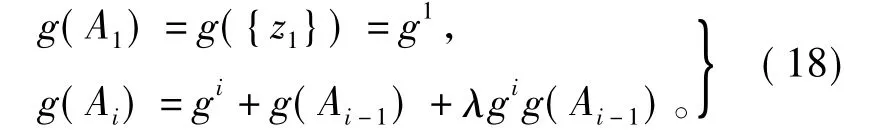
模糊积分运用中，模糊密度度量了信源在融合过程中的重要程度，而h(zi)表示相应输出对于融合结果的可信度。

3.3 Choquet模糊积分动态融合对联络线故障诊断

利用Choquet模糊积分融合联络线故障诊断结论时，设电网被划分为N个部分，局部CE-SVM集合为{CS1，CS2，…，CSN}，对于输入目标ε∈T，第m个模块CSm(m=1，2，…，N)输出的诊断结果dm(ε)= ［dm1(ε)，dm2(ε)，…，dmF(ε)］为一个F维向量，其中dmj(ε)，(j=1，2，…，F)，表示在第m个局部网络的F个故障类别里，CSm得到的ε属于第j个故障类别的后验概率。当电网发生故障且同时触发两个相邻局部CE-SVM模块时，这两个局部CE-SVM会输出各自关于联络线的故障类别后验概率，同时相邻区域间的模糊积分环节被触发。利用Choquet模糊积分融合相邻CE-SVM模块的联络线后验概率输出，从而实现联络线故障的综合决策，更为可靠地识别联络线故障。而Choquet模糊积分运用的核心问题是确定各局部CE-SVM模块的模糊密度［18］。

模糊密度用来度量信源在融合过程中的重要程度。文献［7］用分类精度来刻画区域诊断模块的重要度，但它仅是一个概率统计值，而对于不同的样本，信源表现出来的性能是不同的，单用分类精度度量模糊密度显然是不完备的。因此本文结合工程实际需求，采用算法3所示的模糊密度动态调节算法确定各个局部CE-SVM对不同故障类别的模糊密度，然后对联络线故障进行综合决策。

算法3:动态调节Choquet积分对联络线故障诊断

1)初始模糊密度。利用训练样本计算每一个局部CE-SVM的混淆矩阵——对于F个故障类别，CSm的混淆矩阵是一个F×F的矩阵，记CMm=

将CE-SVM分类结果与实际历史资料构成的训练样本匹配，并对分类效果进行计数，体现在CMm中。其中表示CSm将已知类别样本中第j类误识别成第k类的样本个数。显然对角线元素表示分类正确的样本个数。

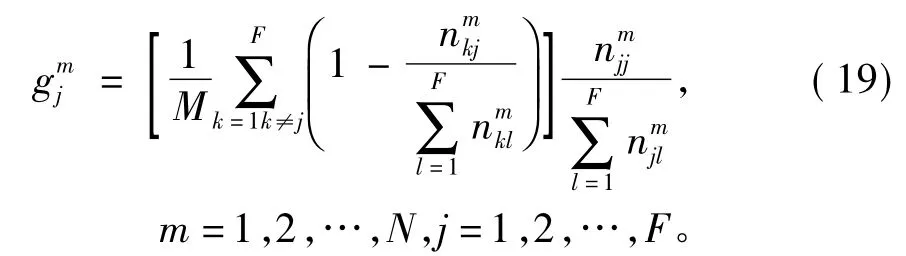
利用CMm和式(19)计算局部CE-SVM的初始模糊密度并从中提取联络线故障的模糊密度上式说明越大，则越小越大，表示判决目标属于类别j时CSm的重要性越大。本文只研究CSm对联络线故障识别的重要性，因此从中提取联络线故障的模糊密度

2)动态调节系数。对于待识别目标ε，根据其实时动态数据，利用式(20)确定模糊密度调节系数αm(ε)，并由式(21)对联络线初始模糊密度调节。

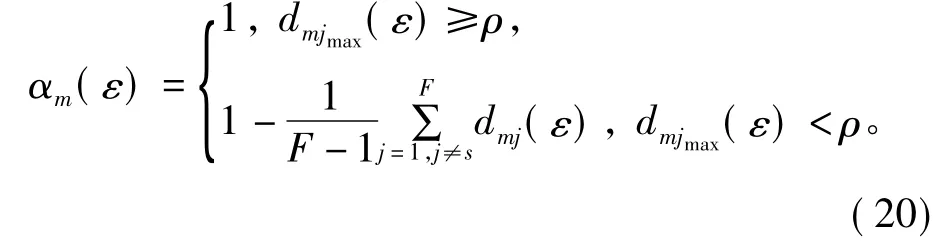
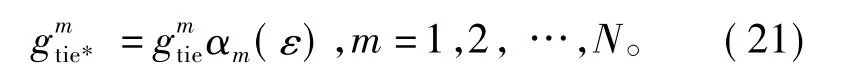
3)模糊积分参数及模糊测度。利用调节后各局部CE-SVM模块关于联络线故障的模糊密度，通过式(16)计算λ的值，并利用递归公式(18)计算模糊测度。

4)信源可信度。将CSm输出的关于联络线故障的后验概率dm，tie(ε)作为模糊积分中的h函数，表示CSm的输出可信度，即h(CSm)=dm，tie(ε)，m= 1，2，…，N。

5)模糊融合。重复1～4步骤得到电网N个局部区域的模糊积分参数，利用式(17)构建相邻区域的Choquet积分环节。当报警信息触发Choquet模糊积分环节后，融合相邻局部CE-SVM对联络线的后验概率，最终采用融合概率值Pe作为相邻局部z模块关于联络线故障的后验概率输出。

4　电网分布式故障诊断策略

实现分布式故障诊断的前提是将大型电力网络分割为连通的子网络［19］。然而常用分区故障诊断方法由于缺少相邻局部电网故障报警信息，从而无法准确判别故障元件。本文采用一种网络重叠的电网分区思路［7］，即联络线分别归属于两个相连的局部电网，而并不是严格归属于某个区域。在离线阶段，依据电网拓扑结构信息以及故障历史数据，构建每个局部电网的CE-SVM诊断模块;当有实时报警信息上传至调度中心时，局部CE-SVM诊断模块实现区域内部的故障元件识别，而相邻两区域间的模糊积分环节融合联络线故障的后验概率，实现联络线故障的综合决策，最后输出诊断结果，完成诊断过程，流程图如图1所示。

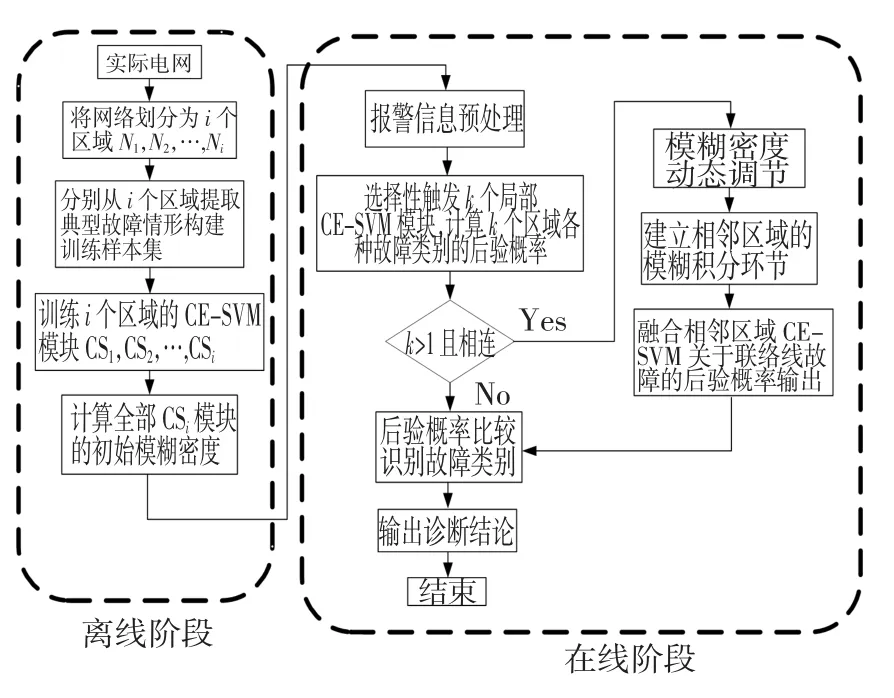
图1　故障诊断流程Fig.1 Flowchart of the fault diagnosismethod

5　算例分析

5.1算例网络介绍

图2测试网络中共有母线、变压器、线路元件28个;断路器40个以及主保护36个，近后备保护24个，远后备保护24个。采用文献［6］的网络分割法将图2所示电力网络分成4个子网络，划分结果如图2虚线所示，其中联络线分别属于关联的两个区域，如联络线L1，即属于子网络1#，又属于2#。网络分区完成后，针对4个局部网络建立局部CESVM诊断模块为{CS1，CS2，CS3，CS4}，构建相连区域的模糊积分环节。本文采用仿真软件Matlab与Libsvm软件包结合的方式设计全部算法流程。

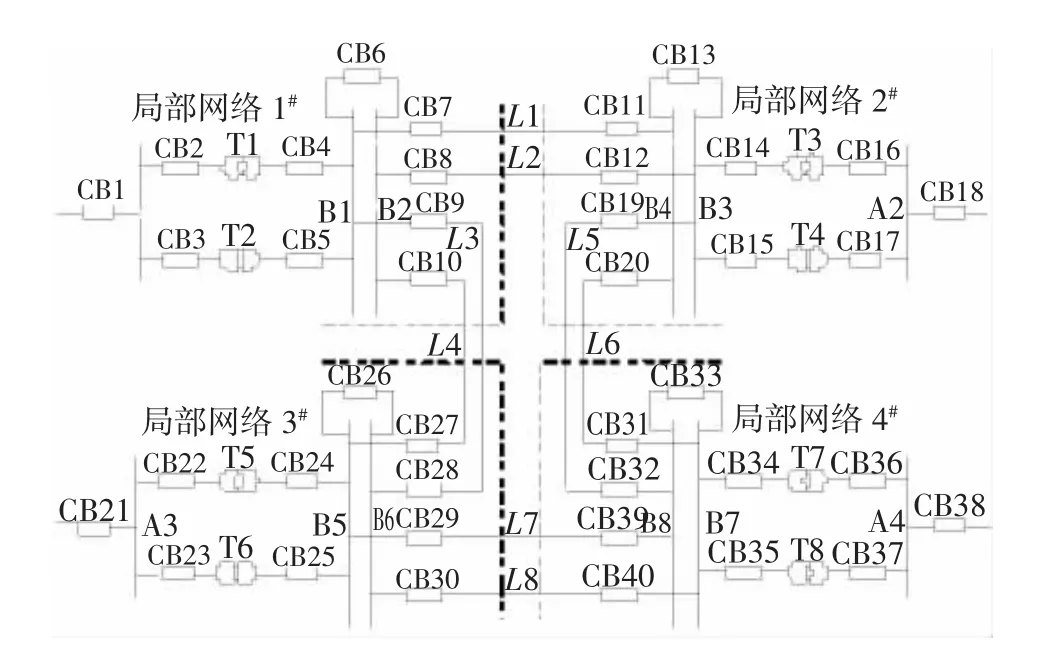
图2　测试网络Fig.2 Test system

5.2局部CE-SVM诊断性能分析

5.2.1 CE算法的优越性

从局部电网1#中提取60个故障样本进行仿真分析，从中选取21个样本作为测试样本，其余39个故障情况作为训练样本。所有保护器和断路器的状态(0或1)作为局部CE-SVM的输入(47个)，选取15个故障类别标签作为输出。仿真过程参数C、δ的变化如图3所示，能够看出SVM惩罚因子C和径向基宽度δ在40代以后就相对稳定的收敛于最优值，得到最优化的惩罚因子C=10.97，径向基宽度δ= 2.78。从图4的种群均值变化曲线也可以看出交叉熵算法40代之后已经能够稳定的收敛于最优的交叉验证概率CV=88.89%，得到的分类正确率为90.48%(19/21)，其中有2个错分样本存在。为分析比较，现从稳定性、收敛性和分类正确率3方面考察CE算法、PSO算法和GA算法优化SVM上的区别，仿真如图4～图6所示。

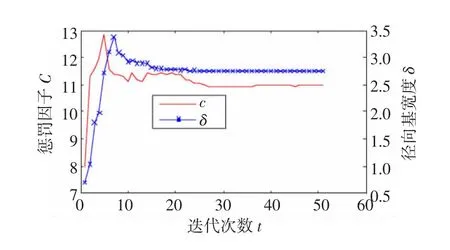
图3　径向基宽度和惩罚因子仿真图Fig.3 Simulation diagram of optim izingδand C

图4　交叉熵算法收敛曲线Fig.4 Population mean of CE algorithm

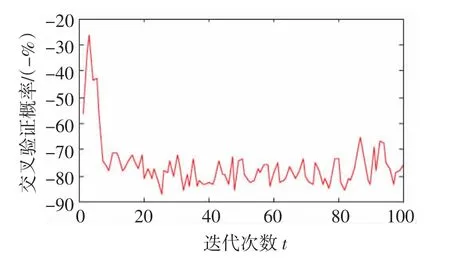
图5　粒子群算法收敛曲线Fig.5 Population mean of PSO

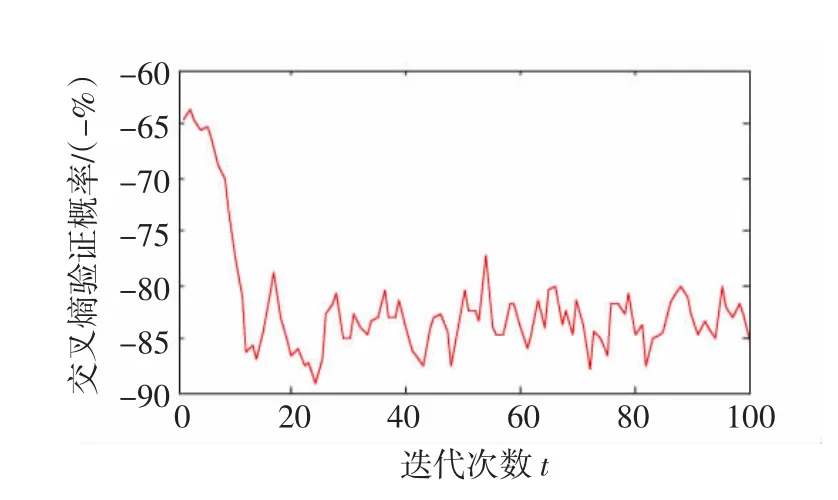
图6　遗传算法收敛曲线Fig.6 Popu lation mean of GA

1)稳定性和收敛性。从图5～图6中可以看出粒子群算法和遗传算法在收敛过程中始终无法稳定的收敛于最优解，种群均值变化范围大，而在图4中，交叉熵算法能够相对稳定的收敛于最优解，种群均值变化范围小，所得到的最优解(SVM参数)更为可靠。多次运行程序，发现CE算法平均在40代前收敛于最优解，而其他智能算法平均在90代前收敛，显然CE算法收敛性要优于其他两种算法。

2)诊断正确率。另从局部网络2#，3#，4#中提取一定数量的训练样本和测试样本，如表1所示，构建不同区域的CE-SVM诊断模块。从表1中可以看出，各种算法对测试样本进行分类时，都存在错分的现象，但相比较来说，交叉熵算法优化的SVM表现出更为优越的故障分类性能。

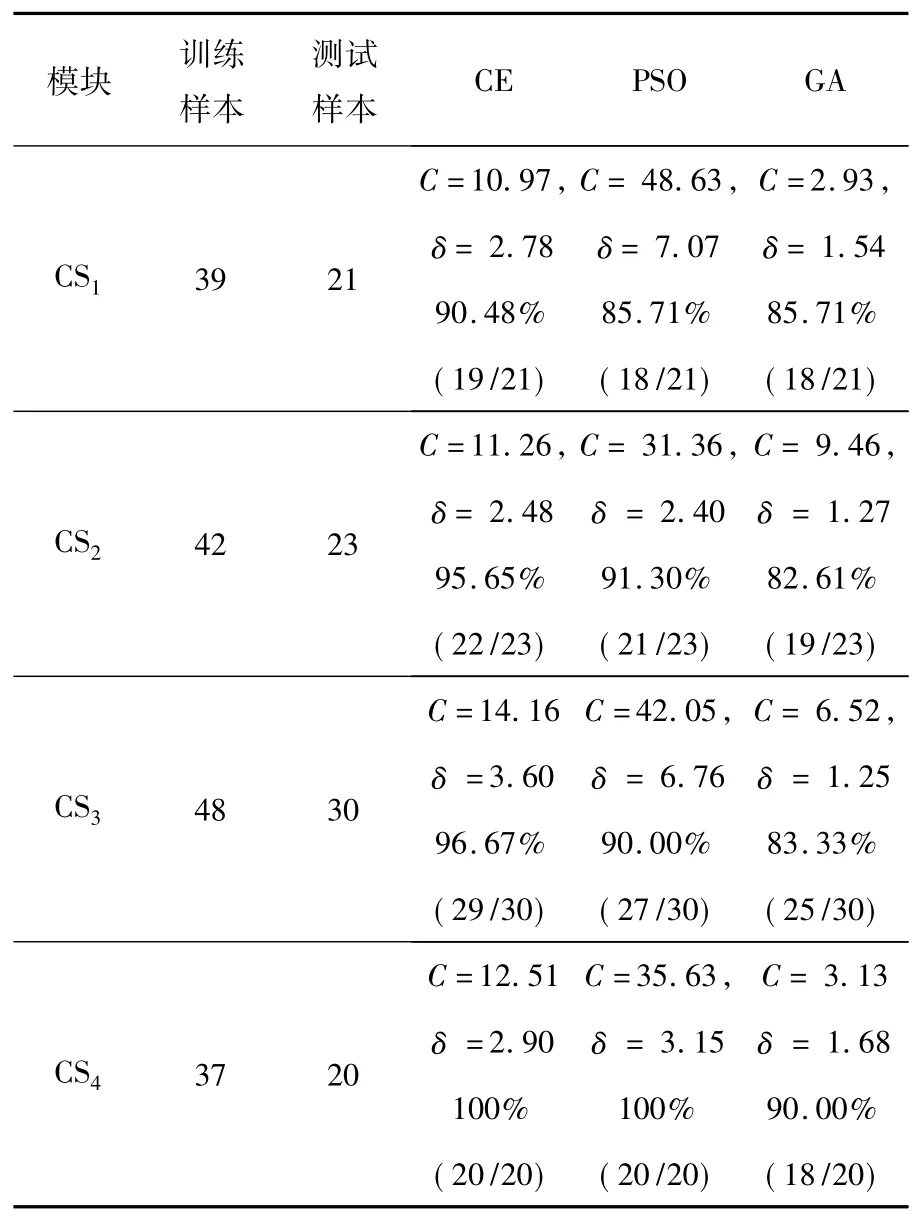
表1　算例网络测试结果Table 1 Test result of test system

5.2.2局部CE-SVM诊断结论

当报警信息限制在局部电网时，需要局部CESVM模块实现网络内部的故障诊断。选取部分故障情形如表2所示，此时仅触发CS1模块。后验概率输出结果如表3所示。从表2中可以看出样本1－3为区域内母线、变压器单重故障，样本4为区域内多重故障，故障情形同时伴有保护器或断路器拒动以及由于某种原因导致的信息缺失的情况。表3测试结果显示局部CE-SVM能够得到正确的诊断结论，具有一定的容错性和较可靠的后验概率输出。为了实时性的考量，将CE-SVM与文献［7］中所用的径向基神经网络故障诊断方法比较，隐层神经元数目为36，训练时间如表4所示。显然本文算法具有较好的实时性，且子网络越复杂，元件越多，效果表现越明显。

值得说明的是:当某一区域同时发生多重故障时，多重故障所属类别标签以及多重故障里的各个元件类别标签的后验概率都维持在相对较高的水平，但这不影响最后的诊断决策正确性;当多重故障分布于不同区域时，分布式故障诊断方法能够将多重故障转化为不同区域的单重故障，并利用相应局部CE-SVM模块进行分布式故障诊断，从而提升诊断效率，降低计算复杂程度。

表2　CS1测试样本Table 2 Test samples of CS1

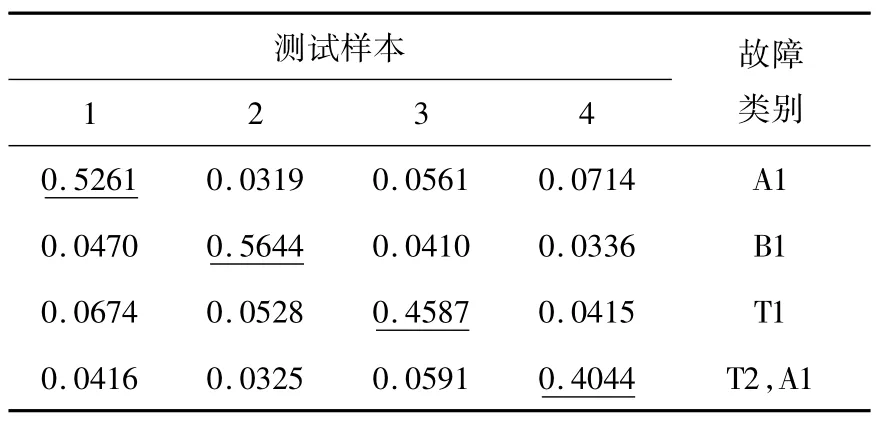
表3　测试结果Table 3 Test result

表4　CE-SVM与RBF神经网络训练时间比较Table 3 Com parison for time between CE-SVM and RBF

5.3模糊积分融合环节

模糊积分应用的关键在于确定两个参数:信源的模糊密度和信源关于某个样本的可信度输出。本文采用算法2的模糊密度动态调节算法确定局部CE-SVM模块的模糊密度;以各区域CE-SVM模块关于某个样本的后验概率输出，作为相应的可信度输出。以区域1#和区域2#间的联络线L1、L2为例:采用算法2求解动态调节后的模糊密度、参数λ以及模糊测度值如表5所示(联络线L1的诊断内容为表6和表7中的样本1)。采用同样方法能够得到动态调节后所有区域关于联络线故障类别的模糊积分参数。

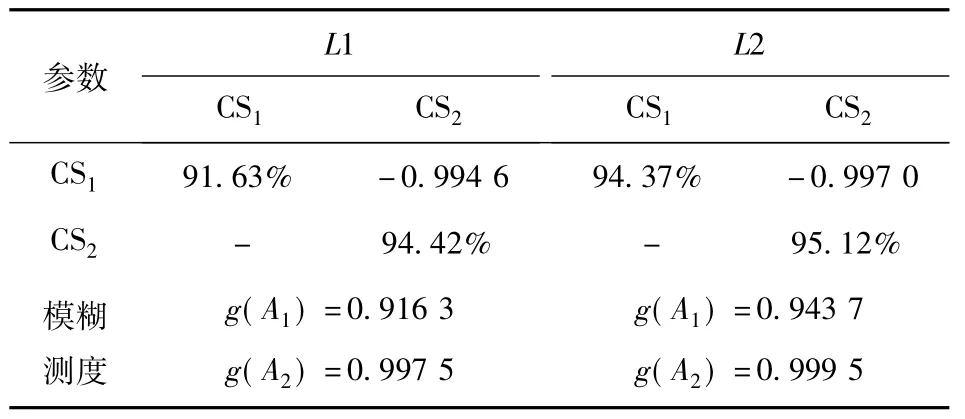
表5　联络线L1、L2模糊积分参数的确定Table 5 Parameters setting of fuzzy integral of L1 and L2

另外，从图1测试网络中提取故障情形如表6所示，此时报警信息不再局限于某一个区域，而是同时波及多个区域，导致相邻区域间的模糊积分环节被触发。局部CE-SVM在完成各自诊断任务的条件下，模糊积分环节融合相邻区域的CE-SVM模块关于联络线故障的后验概率输出。

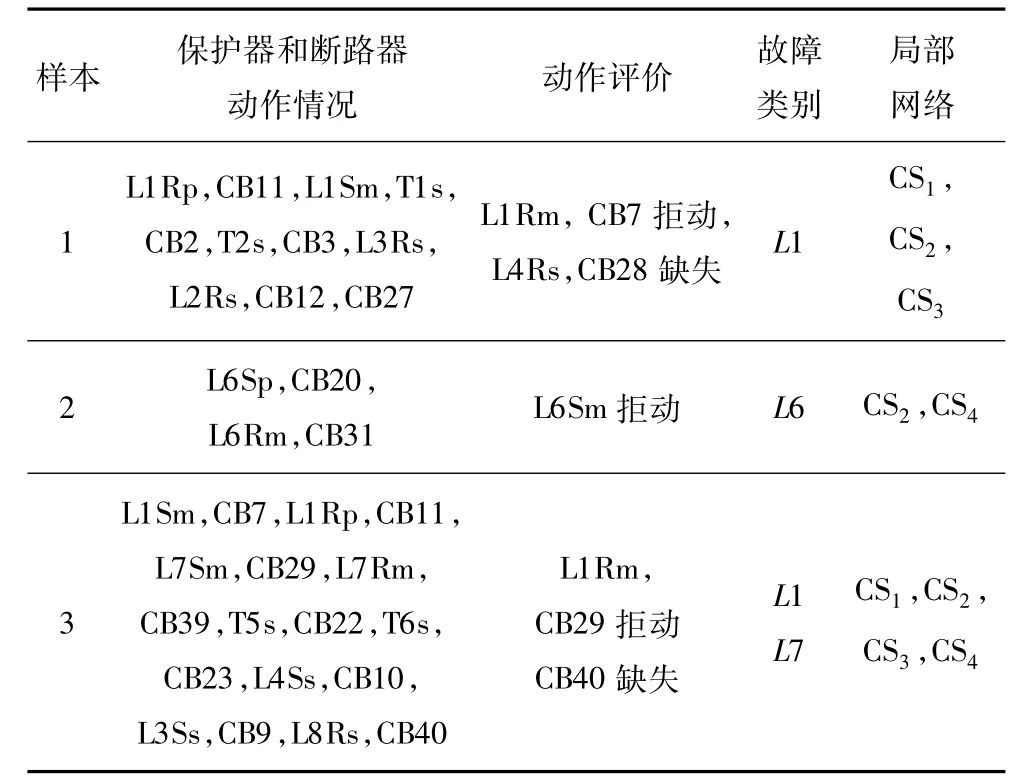
表6　多区域测试样本Table 6 Test samp le in multi-region

样本1－2为单重故障且故障报警信号触发多个区域诊断模块的情况，模糊积分关联融合各局部CE-SVM关于联络线的故障诊断后验概率，诊断结果如表7所示。表7列出连接相邻区域的联络线后验概率输出和模糊积分融合结果。当联络线发生复杂故障，如保护装置不正确动作或信号丢失导致故障范围扩大时，若只利用单一区域网络接收到的故障信号进行诊断，易导致故障类别后验概率较低(如样本1中CS2输出的L1故障后验概率)，降低故障识别正确率。此时利用模糊积分环节对诊断结论做进一步综合决策，能够有效克服上述不足。样本6为多重故障并触发多个区域CE-SVM诊断模块情况，同时伴有保护装置拒动和信号丢失的情况，此时对电网故障诊断提出了更高的要求，诊断结果如表8所示。故障元件分布在不同区域的情况，分区故障诊断策略能够将全网多重故障转为针对相邻网络间联络线或网络内部的单重故障，进而利用相应区域的诊断模块分区诊断。

诊断结果显示，报警信息触发多个CE-SVM模块时，模糊积分环节能够融合相邻区域间联络线的后验概率，实现故障诊断的综合决策，并且在保护或断路器拒动时，本文方法仍能有效诊断故障元件。

表7　单重故障诊断结果Tab le 7 Diagnosis resu lts of single fault cases

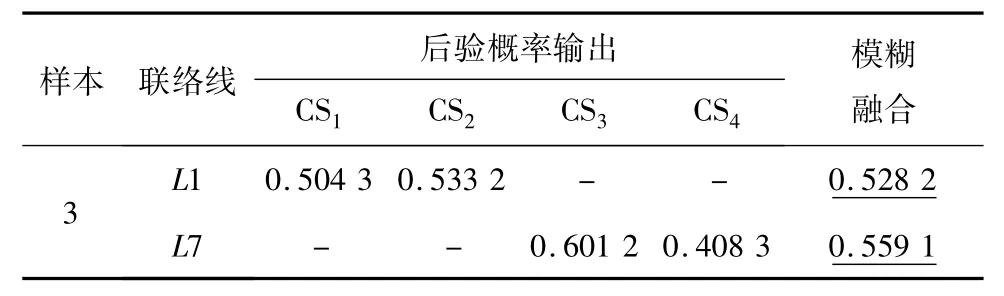
表8　多重故障诊断结果Table 8 Diagnosis results ofmultiple fault cases

需要说明的是:采用本文的局部CE-SVM模块对某一输入样本进行故障识别时，得到对应全部训练样本中故障类别的后验概率值总和为1，显然后验概率取值大小与训练样本的故障类别数有关，但无论这个类别数是多少，都不影响局部CE-SVM的分类效果，后验概率最大值所对应的故障类别始终作为CE-SVM输出的分类结果，而表1的算例仿真结果也表明本文诊断方法对不同区域的不同故障类别均具有良好的故障分类准确率。但是在模糊积分融合的过程中，要求由于不同区域故障类别数的差异，造成的相邻CE-SVM模块对于联络线后验概率输出的差别尽量小，这样可以提升诊断模型的容错性，而选用合理的网络分区算法将电网划分为均匀连通的子网络，可以改善此类问题。另外分区不同带来的影响主要体现在模糊积分环节的参数设定与诊断模型结构方面，对CE-SVM的局部故障诊断能力影响很小。显然深入具体地分析不同分区算法对本文诊断方法的影响是十分有意义的，所以作者下一步研究的主要内容就是对网络分区算法的研究，使得网络分区与SVM和模糊积分融合的故障诊断过程相协调，进一步提升诊断方法的容错性。

6　结论

本文采用分布式的思想，针对当前大电网故障诊断问题时面临的两个主要问题:即分区后局部故障诊断问题和联络线故障诊断问题，提出了一种基于CE-SVM和模糊积分相结合的有效解决办法。CE算法可以有效防止SVM参数陷入局部最优，提升电网局部故障诊断能力;模糊积分将局部CESVM先验信息与后验概率关联融合，对联络线的故障具有良好的诊断效果。仿真算例表明:该方法对于识别网络内部故障或联络线故障都有较好的效果，同时在少量信息缺失或错误的情况下仍能得到准确的诊断结论。本文下一步研究内容将主要集中在电网结构分区算法对故障诊断影响等方面。

参考文献:

［1］PARK Y M，KIM GW，SOHN JM.A logic based expert system (LBES)for fault diagnosis of power system［J］.IEEE Transactions on Power Systems，1997，12(1):363－369.

［2］CARDOSO G J，ROLIMJG.Applications of neural network modules to electric power system fault section estimation［J］.IEEE Transactions on Power Delivery，2004，19(3):1034－1041.

［3］张岩，张勇，文福拴，等.容纳时序约束的改进模糊Petri网故

障诊断模型［J］.电力系统自动化，2014，38(5):66－72.

ZHANG Yan，ZHANG Yong，WEN Fushuan，et al.Power system fault diagnosis with an enhanced fuzzy petri net accommodating temporal constraints［J］.Automation of Electric Power Systems，2014，38(5):66－72.

［4］郑蕊蕊，赵继印，赵婷婷，等.基于遗传支持向量机和灰色人工

免疫算法的电力变压器故障诊断［J］.中国电机工程学报，2011，31(7):56－63.

ZHENG Ruirui，ZHAO Jiyin，ZHAO Tingting，etal.Power transformer fault diagnosis based on genetic support vectormachine and gray artificial immune algorithm［J］.Proceedings of the CSEE，2011，31(7):56－63.

［5］PELLACO L，COSTAMAGNA P，GIORGIA D.Fault diagnosis

in fuel cell systems using quantitative models and support vector machines［J］.Electronics Letters，2014，50(11):824－826.［6］毕天姝，焦连伟，严正，等.用于分布式故障诊断系统的新型

网络分割法［J］.电力系统自动化，2001，35(16):16－21.

BITianshu，JIAO Lianwei，YAN Zheng，et al.Graph partitioning method for distributed fault section estimation system in power network［J］.Automation of Electric Power Systems，2001，35(16): 16－21.

［7］石东源，熊国江，陈金富，等.基于径向基函数神经网络和模

糊积分融合的电网分区故障诊断［J］.中国电机工程学报，2014，34(4):562－569.SHIDongyuan，XIONG Guojiang，CHEN Jinfu，et al.Divisional fault diagnosis of power grids based on RBF neural network and fuzzy integral fusion［J］.Proceedings of the CSEE，2014，34 (4):562－569.

［8］VAPINKW N.The nature of statistical learning theory［M］.Australia:Springer-Verlag New York Inc，1999:11.

［9］REUVEN Y R.The cross-entropy method:a unified approach to combinatorial optimization［M］.Australia:Springer-Verlag New York Inc，2004.

［10］PIETER T D，REUVEN Y R.A tutorial on the cross-entropy method［J］.Annals of Operations Research，2005，134(2):19 －67.

［11］PLATT J.Probabilistic outputs for support vector machines and comparison to regularized likelihood method［C］//Advance in Large Margin Classifier，Cambridge.MA:MIT press，2000:61 －74.

［12］HASTIE T，TIBSHRANIR.Classification by pairwise coupling ［J］.The Annals of Statistics，1998，26(1):451－471.

［13］WU T F，LIN C J，WENG R C.Probability estimates formulticlass classification by pairwise coupling［J］.Journal of Machine Learning Research，2004，5:975－1005.

［14］郭创新，游家训，彭明伟，等.基于面向元件神经网络与模糊

积分融合技术的电网故障智能诊断［J］.电工技术学报，2010，25(9):183－190.

GUO Chuangxin，YOU Jiaxun，PENG Mingwei，et al.A fault intelligent diagnosis approach based on element-oriented artificial neural networks and fuzzy integral fusion［J］.Transactions of China Electrotechnical Society，2010，25(9):183－190.

［15］KWAK K C，PEDRYCZW.Face recognition:a study in information fusion using fuzzy integral［J］.Pattern Recognition Letters，2005，26(6):719－733.

［16］SUGENO M.Theory of fuzzy integrals and its applications［D］.Tokyo:Tokyo Institute of Technology，1974.

［17］MUROFUSHI T，SUGENO M.An interpretation of fuzzy meas

ures and the Choquet integral asan integralwith respect to a fuzz

ymeasure［J］.Fuzzy Sets and Systems，1989，29(2):201－227.［18］邢清华，刘付显.一种基于模糊密度动态调节的融合目标识

别方法［J］.控制与决策，2009，24(5):777－780.

XING Qinghua，LIU Fuxian.Method of fusion target recognition based on fuzzy densities dynamic adjusted［J］.Control and Decision，2009，24(5):777－780.

［19］MCAFFREY JD.Graph partitioning using a Simulated Bee Colony algorithm［C］//Information Reuse and Integration(IRI)，2011 IEEE International Conference on，Aug.3－5，2011，Las Vegas，NV.2011:400－405.

(编辑:刘琳琳)

Fault diagnosis of power networks app lying CE-SVM and fuzzy integral fusion

BIAN Li，BIAN Chen-yuan
(School of Electronic and Information Engineering，Heilongjiang University of Science and Technology，Harbin 150022，China)

Abstract:A fault diagnosis method for power networks based on posterior probability CE-SVM and fuzzy integral dynamic fusion was proposed.The aim was to solve the problem of division fault diagnosis inside the local network and for the tie lines connecting local network.Firstly，a graph partitioningmethod was used to the large power network into connected sub-networks with balanced working burdens.Historical data was applied to train local CE-SVMs and local CE-SVM moduleswere selectively triggered according to local alarm information.Fuzzy integral fusion department constructed by fuzzy densities dynamic adjusted algorithm was used to fuse posterior probability of the tie lines fault that outputted by local CE-SVM modules for tie line fault identification.The method can notmerely diagnose the faults inside local network，but also solve the fault diagnosis problem of tie lines.The simulation results indicate that the proposed method is effective and have good fault tolerance under action information losing or unwanted operation of protector and circuit breaker.

Keywords:distributed;large power networks;fault diagnosis;cross entropy;support vector machine; fuzzy integral

通讯作者:边晨源

作者简介:边莉(1978—)，女，博士，副教授，研究方向为阵列信号处理、人工智能技术;

基金项目:黑龙江省自然科学基金(QC201003);黑龙江科技大学青年才俊资助计划

收稿日期:2014－09－24

中图分类号:TM 71

文献标志码:A

文章编号:1007－449X(2016)02－0112－09

DOI:10.15938/j.emc.2016.02.016