基于CM F-EEMD的风电齿轮箱多故障特征提取

王志坚，韩振南，宁少慧，梁鹏威(太原理工大学机械工程学院，山西太原030024)



基于CM F-EEMD的风电齿轮箱多故障特征提取

王志坚，韩振南，宁少慧，梁鹏威
(太原理工大学机械工程学院，山西太原030024)

摘要:针对EMD(empiricalmode decomposition)模态混叠现象和由于所添加白噪声幅值单一而影响EEMD(ensemble empiricalmode decomposition)分解精度等问题，提出了一种新的信号处理方法CMF-EEMD。CMF(combined mode function)将EMD分解得到敏感的IMFs按高低频进行组合，形成两个包含高低频的本征模态函数Ch和CL，然后通过添加不同的白噪声幅值对Ch和CL分别进行EEMD分解，最后对敏感的IMFs进行循环自相关函数解调分析。将提出方法应用于仿真信号和风力齿轮箱试验台的振动信号，成功提取了多故障特征频率，验证了此方法的有效性。并通过与添加单一白噪声幅值进行对比分析，凸显此方法具有更高的分解精度。

关键词:风电齿轮箱;组合模态函数;总体平均经验模态分解;多故障;循环自相关函数

韩振南(1958—)，男，教授，博士生导师，研究方为机械故障诊断分析;

宁少慧(1978—)，女，博士，讲师，研究方向为机械故障诊断;

梁鹏威(1990—)，男，硕士，研究方向为机械故障诊断。

0　引言

在旋转机械零部件出现局部损伤时，工作过程中会出现间断性的脉冲冲击激振，如轴承，转子等［1－2］。这种冲击成分的能量是周期性变化的，但故障脉冲信号往往被淹没在工频振动、背景噪声、其他零部件的振动谐波中，因此冲击能量的时域提取显得非常困难。多故障共存时多冲击信号持续时间短，频带很宽，特征频率出现相互交叉现象，往往导致误诊断发生。经验模态分解(empirical mode decomposition，EMD)［3］被广泛的用在旋转机械多故障诊断中，能高效地分析非平稳非线性信号，能将信号从高频到低频分解成有限个具有物理意义的固有模态函数(intrinsic mode functions，IMFs)和余项之和，IMFs的带宽由信号本身决定，但是由于模态混叠现象使其分解的结果不够精确［4］。模态混叠是指在同一个IMF中包含差异极大的特征时间尺度，或者接近的时间尺度分解在不同IMF中［5－6］，为了避免该现象，Wu和Huang又提出了总体平均经验模态分解(ensemble empirical mode decomposition，EEMD)［7］。通过对原信号添加不同白噪声并重复的求IMFs的均值来提高EMD的分解精度，如何选取合适的白噪声幅值非常重要，幅值过小不足以改变极值点的分布，过大会造成过分解，同样会产生模态混叠现象，因此单一的白噪声幅值会直接影响到EEMD分解精度［8］。

针对以上方法的缺点，本文提出了CMF-EEMD，组合模态函数(combined mode function，CMF)将原信号分解成两个新的组合模态函数Ch和CL。它们分别代表原信号的高频和低频成分。通过确定合适的白噪声幅值来提高EEMD的分解精度。此外，齿轮箱多故障振动信号往往是多调制源多载波信号共存，用循环自相关函数(cyclic autocorrelation function，CAF)解调方法处理复杂信号时，循环域的高频处由于载波频率比较接近而出现交叉项［9］。CMF-EEMD可将比较接近的时间尺度分解在不同的IMFs中，在一定程度上弥补了交叉项的干扰。最后将CMF-EEMD分解后能量相对集中的IMFs进行循环自相关函数解调分析，将该方法应用于风电齿轮箱故障诊断中可以有效地分离出各状态下的故障特征频率。

1　CMF-EEMD的基本原理

1.1 CM F

由EMD得到的IMFs C1，C2，…，CI，包含了从高到低不同的频带［10］，CMF将相邻的IMFs叠加组成Ch和CL。本文中Ch为含有高频成分IMFs的叠加结果，CL为剩余IMFs的叠加结果。重组相邻的含有高频成分的IMFs得到Ch为

其中，m是含有高频IMF的最大层数。

重组相邻的含有低频成分的IMFs得到CMF CL

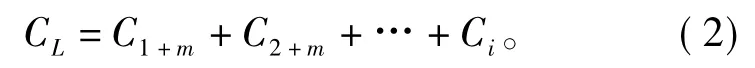
其中，m＜i≤n，n为EMD敏感IMFs的最大层数。

关于如何确定含有高频成分的最大层数，论文从以下两个角度分析的。

EMD能自适应的将信号按高低频依次分开，分别对其进行FFT变换，能得到不同的频带。

考虑到循环自相关函数解调的结果:在整个循环域内可将循环频率分为高低频两部分，低频处主要包含调制频率或其二倍频，在高频处主要以载波频率的二倍频为中心以调制频率为边频带的频率簇。

因此本文以调制频率(一般为轴的转频)或其倍频作为高低频分界线。

1.2 EEMD

EMD中由于极值点分布不均导致模态混叠现象。为此，Wu等［4］将原信号中加入白噪声来平滑异常现象的出现，不仅利用了白噪声频谱均匀分布使不同的时间尺度的信号自动分布到合适的参考尺度上，而且也利用了白噪声的零均值特性，经过多次平均将噪声相互抵消，从而消除了噪声对原信号的影响。EEMD步骤如下:

1)给定一个原信号x(t)，加入均值为零、幅值标准差为常数的白噪声nj(t)，j=1，2，3，…，M。

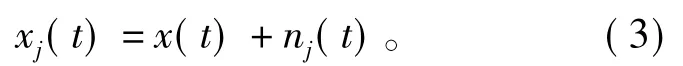
2)用EMD分解xj(t)得到I个(IMFs)Ci，j，(i= 1，2，3，…，I)，其中Ci，j表示第j次加入白噪声幅值后，分解得到的第i个IMF。

3)如果j＜M令j=j+1重复步骤2。

4)最终得到EEMD分解的IMFs为

5)输出Ci(i=1，2，3，…，I)作为EEMD得到的第i个IMF。

所加噪声的幅值c直接影响EEMD分解精度［11－14］。若在EEMD分解的过程中加入单一的白噪声幅值，过大时会影响原信号的高频成分的极值点的分布，若幅值太小，则不能有效消除原信号的间断现象［7－14］。到目前为止，在不丢失原信号信息的基础上，仍没有一个关于白噪声幅值选取的自适应方程［15－16］。一般情况下所加白噪声幅值是原信号标准差的0.2倍［7－17］，但根据经验和大量的仿真信号可知，0.2并非适合所有的信号，当原信号主频成分为高频时，c要小于0.2，反之c要大于0.2。因此对本文中含有高频的Ch分解时，c=0～0.2;含有低频的CL分解时c=0.2～0.5。

本文选用相关系数法，计算各IMF与原信号的归一化相关系数［18］，设定较小的阈值目的使Ch和CL尽可能保持原信号的完整性。此外本论文采用在执行EMD总次数为100的前提下，用逐步逼近法来确定仿真和实测信号的c值，提取多故障的流程图如图1所示。

图1　CMF-EEMD流程图Fig.1 Flow chart of CM F-EEMD

2　仿真实验分析

当齿轮箱发生故障时，其振动信号往往表现为调制信号［6］，为了提取振动信号的故障特征，需要对其进行解调分析。例如，给定一个多调制源多载波频率的仿真信号(5)，采样频率fs=600 Hz，采样点数1 024，调制频率为fn1=8 Hz，fn2=15 Hz，fn3= 10 Hz，fn4=12 Hz，载波频率fz1=80 Hz，fz2=130 Hz。

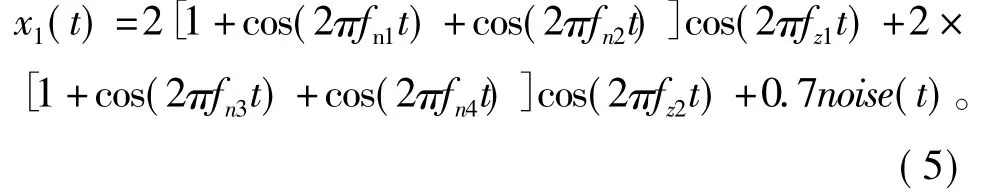
仿真信号的时域波形如图2(a)所示，包含着大量不易区分的周期成分，循环自相关函数解调如图2(b)，显然循环频率fn1=8 Hz和2fz1=160 Hz为主频成分，但在高频处2fz2=260 Hz没有明显的谱峰，而且出现了200 Hz和260 Hz的交叉项;在低频处(fn3+ fn4)=22 Hz，2(fn1+fn4)=40 Hz，2(fn2+fn3)+fn4= 62 Hz分别为调制频率的和及其倍数，它们在解调谱中易表现为无法区分且引起误诊断的频率成分。

图2　仿真信号时域波形和循环自相关函数Fig.2　Time-domain and cyclic autocorrelation function waveform of simulation signal

为了继续提取特征频率，c=0.2时对仿真信号EEMD分解如图3所示，对相关性强的前6层IMFs进行循环自相关解调分析如图4:在高频处频率成分2fz2=260 Hz，2fz1=160 Hz对应仿真信号载波频率;在低频处fn1=8 Hz，fn3=10 Hz为原信号的调制频率。但是22 Hz、36 Hz、38 Hz、72 Hz和76 Hz仍然是调制频率之和或和的倍数，依然不易区分，调制频率fn2=15 Hz，fn4=12 Hz也没有分离出来，且在调制频率160 Hz并无分解到两个不同的IMF中。以上结果与EEMD处理时c的选取有关，为此用本文提到的方法继续进行分析。

将原信号进行EMD分解得到相关性最强的前7层模态函数如图5(a)，分别对其进行FFT变换，发现前两层为高频成分，由于篇幅的限制在此不做图像说明。叠加前两层作为高频成分Ch，叠加后5层作为低频成分CL。Ch和CL经过EEMD分解时c值分别取0.05和0.5，结果如图5(b)和图5(c)。图5(b)的前6层循环自相关函数解调分析，结果如图6(a～f)所示，高频处频率成分2fz2=260 Hz，2fz1=160 Hz分解在两个不同的IMFs中，低频处调制频率fn3=10 Hz，2fn3=20 Hz，fn1=8 Hz，2fn1=16 Hz，fn4=12 Hz逐一凸显出来。对图5(c)的前5层进行循环自相关分析，结果如图7(a～e)，显然低频处除了图6显示的调制频率外，2fn2=30 Hz，fn2= 15 Hz表现明显。综上分析，对不同的高低频带确定不同的白噪声幅值，通过循环自相关函数分析，无论高频还是低频处追踪效果都有明显改进。为下面的实测信号的特征提取提供理论依据。

图3　仿真信号当c=0.2时EEMD分解结果Fig.3 Decomposition results using EEMD when c=0.2

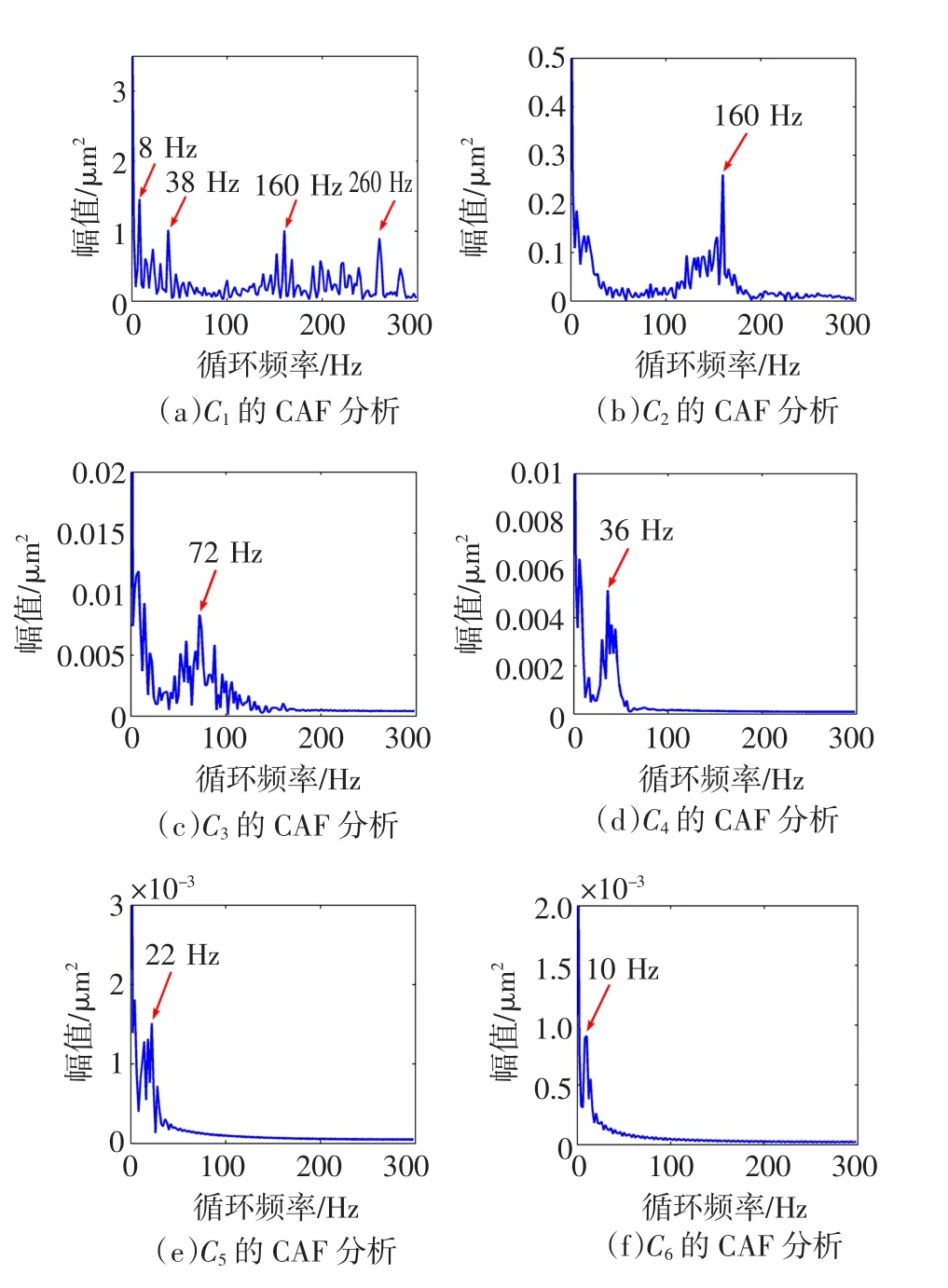
图4　当τ=0时对IMFs进行CAF分析Fig.4　Cyclic autocorrelation function of the IMFs w ith EEMD whenτ=0

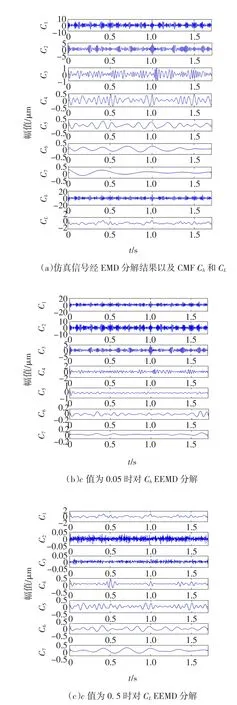
图5　仿真信号EMD分解结果以及Ch和CL的EEMD分解Fig.5 Decomposition results using EMD and decomposition results for Chand CLw ith EEMD

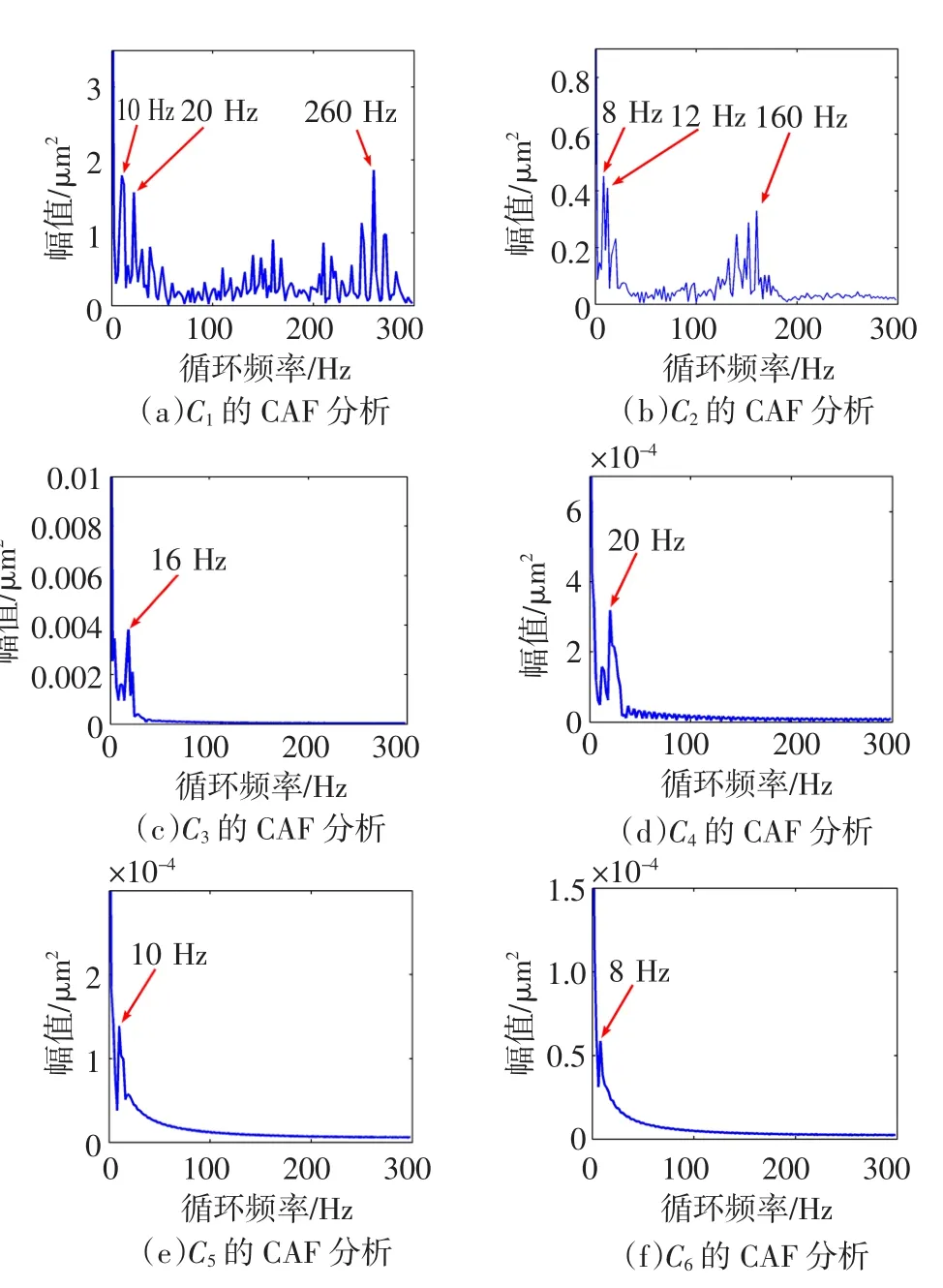
图6　当τ=0时对Ch的IM Fs进行CAF分析Fig.6　Cyclic autocorrelation function of ChIMFs w ith EEMD whenτ=0

幅

值

/μ

m2

图7　当τ=0时对CL的IMFs进行CAF分析Fig.7　Cyclic autocorrelation function of CLIM Fs w ith EEMD whenτ=0

3　风电齿轮箱振动信号分析

某公司风力发电机齿轮箱试验台的结构如图8所示。1～4分别代表电动机、齿轮箱、联轴器和发电机，发电机作为齿轮箱负载，#1、#2等代表轴承编号。其中#6、#8、#10内外圈点蚀，#7内圈点蚀。采用加速度传感器和动态信号分析仪对其进行测量分析，采集点位于高速轴齿轮箱轴承座。采样点数1 024，采样频率10 000 Hz。输出齿轮轴转速为1 728 r/min，转动频率为28.8 Hz(调制频率)，中间级齿轮轴转动频率为7.04 Hz(调制频率)部分轴承转速与故障频率的数据如表1所示。

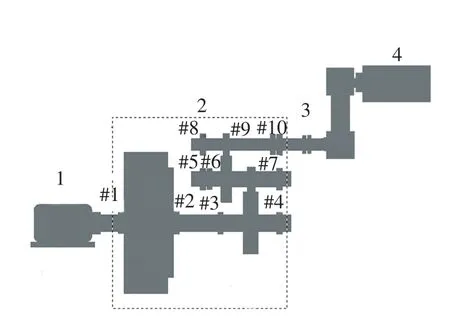
图8　风电齿轮箱试验台简图Fig.8 Schem atic of w ind turbine gearbox test rig

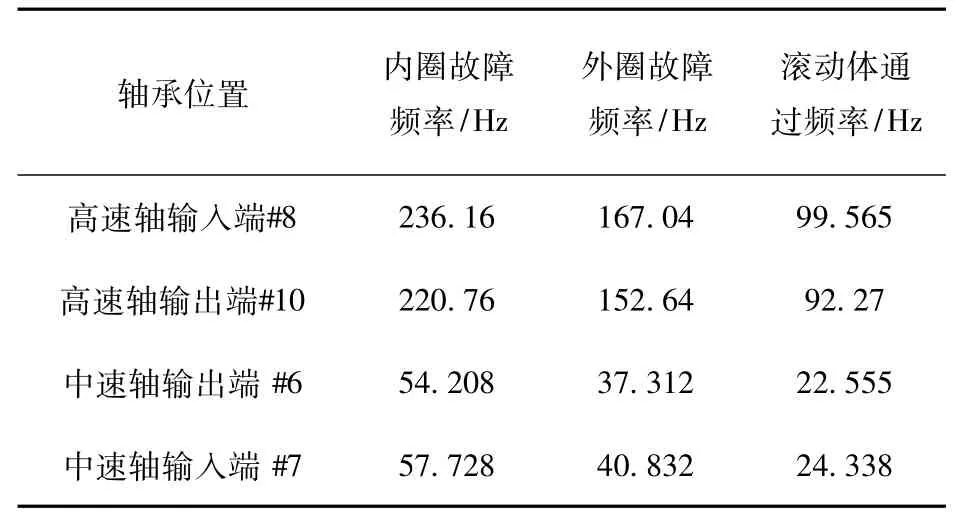
表1　轴承故障频率Table 1 Characteristic frequency of rolling bearing

分别采集空载和强载荷下#10轴承座加速度传感器数据，振动波形如图9(a)和图9(b)，其中图9(a)无明显周期成分，振动幅值较小。当电机加载到1 880 kW时，振动和噪声显著提高，短时间内高速轴输出端升温迹象明显。由图9(b)可知，存在两个明显的振动周期，分别是0.035 6 s和0.004 5 s，对应于频率28 Hz和220 Hz，且前者幅值明显高于后者，它们分别为高速轴的转频和高速轴输出端#10轴承内圈故障频率。分别对其进行循环自相关解调如图10所示，结果与图9完全吻合。

图9　#10轴承座采集的信号Fig.9 The vibration signal of bearing block#10

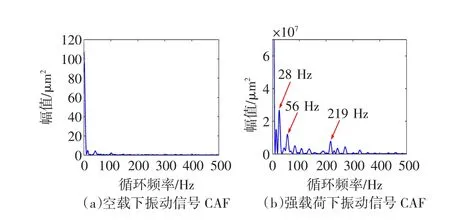
图10　振动信号CAF分析Fig.10 Cyclic autocorrelation function for vibration signal at whenτ=0

为了进一步提取其他故障特征，对上述强振动信号用本文提出方法进行分析。将振动信号进行EMD分解得到相关性最强的前6层模态函数如图11(a)，分别对其进行FFT变换，发现前两层为高频成分。叠加前两层作为高频成分Ch，叠加后4层作为低频成分CL。Ch和CL经过EEMD分解时c值分别取0.1和0.5，结果如图11(b)和图(c)。图11(b)的前4层循环自相关函数解调分析，结果如图12(a～d)所示，低频处，高速轴的转动频率28 Hz以及二倍频57 Hz明显凸出。高频处219 Hz、114 Hz、238 Hz、353 Hz、107 Hz分别对应高速轴#10轴承内圈故障频率、中速轴#7轴承内圈故障的二倍频、高速轴#8轴承内圈故障频率以及外圈故障二倍频、#6轴承内圈故障二倍频。显然Ch包含了大量的故障信息，同时对图11(c)的前5层进行循环自相关解调分析如图13，低频处循环频率与图12完全一致。在高频处除了图12出现的循环频率外，还包括302 Hz和73 Hz，分别为#10轴承外圈故障频率二倍频和#6轴承外圈故障频率二倍频。在强载荷作用下，高速轴因刚度不足而发生了微小变形，其振动信号最为强烈，从高速轴输出端到中速轴振动信号逐渐减弱。此外当c=0.2时，只对原信号进行EEMD分解，通过对比分析，发现在低频处与图12和图13信息完全一致，但高频处部分特征频率依然被淹没在噪声之中。显然c值得选取影响EEMD的分解精度。

图11　振动信号EMD分解结果以及Ch和CL的EEMD分解Fig.11 Decomposition results using EMD and decom position results for Chand CLw ith EEMD

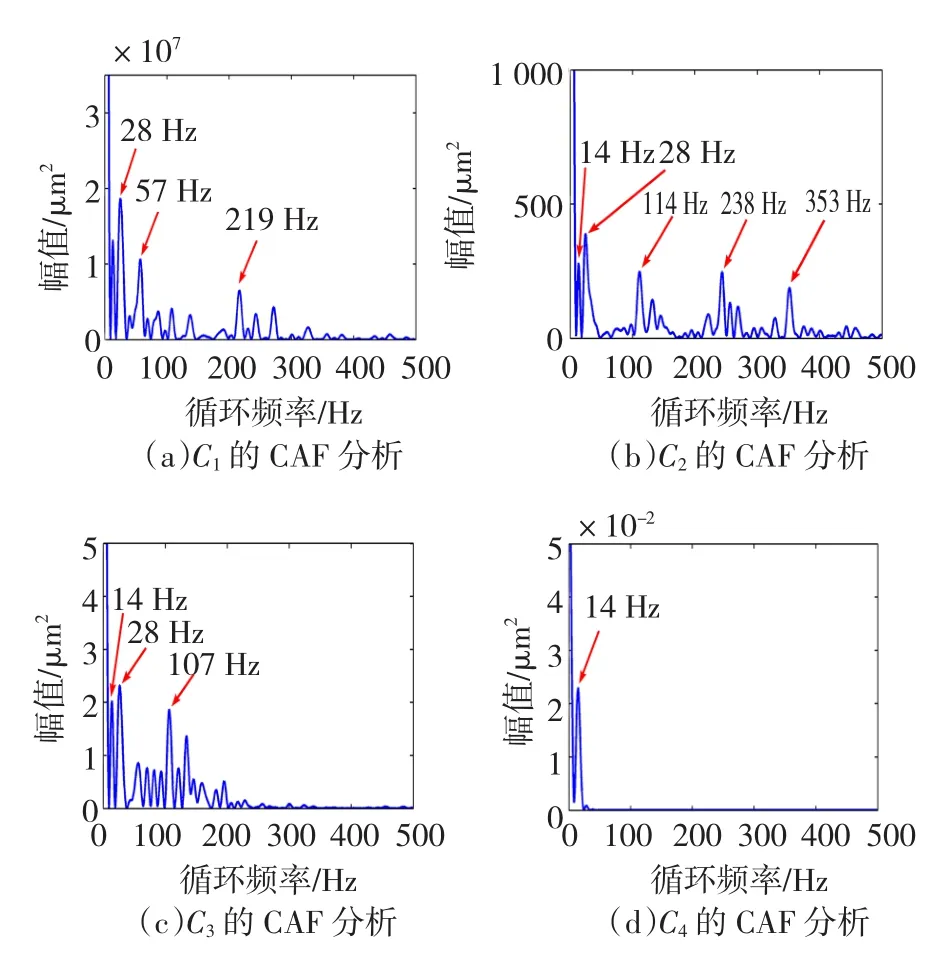
图12　当τ=0时对Ch的IMFs循环自相关函数解调分析Fig.12　Cyclic autocorrelation function of ChIMFs w ith EEMD whenτ=0

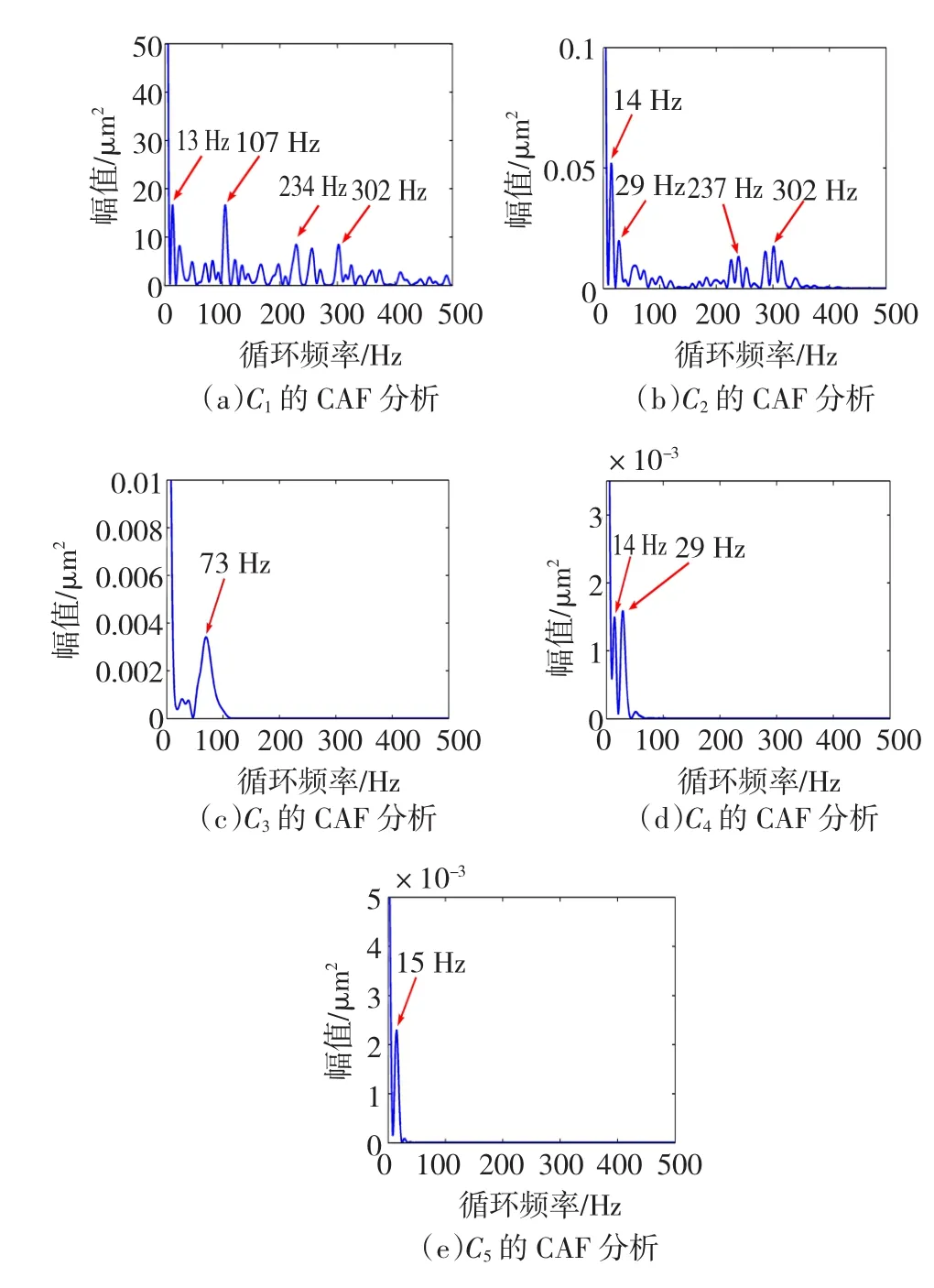
图13　当τ=0时对CL的IM Fs进行CAF分析Fig.13　Cyclic autocorrelation function of CLIMFs w ith EEMD whenτ=0

4　结论

1)文章提出CMF-EEMD方法，弥补了EEMD由于所加白噪声幅值单一而出现的分解精度低等问题，通过多调制源多载波频率的仿真信号验证了方法的可靠性。

2)CMF-EEMD用于多故障共存(轴承6#、7#、8#、10#内外圈点蚀，高速轴微小弯曲)的风电齿轮箱中，且逐一识别出故障位置。

参考文献:

［1］孙斌，王艳武，杨立.基于红外测温的异步电机轴承故障诊断［J］.电机与控制报，2012，16(1):50－55.SUN Bin，WANG Yanwu，YANG Li.Study of fault diagnosis of induction motor bearing based on infrared inspection［J］.Electric Machines and Control，2012，16(1):50－55.

［2］王国富，张海如，张法全，等.时频压缩随机共振用于转子故障早期检测［J］.电机与控制学报，2011，15(6):38－44.WANGGuofu，ZHANGHairu，ZHANG Faquan，etal.Frequency compression of SR for detecting rotor’s incipient fault signal［J］.Electric Machines and Control，2011，15(6):38－44.

［3］FlANDRIN P，RILLING G，GONC-ALVE’S P.Empiricalmode decomposition as a filter bank［J］.IEEE Signal Processing Letters，2004，11(2)，112－114.

［4］LIH，YANG L，HUANG D.The study of the intermittency test filtering character of Hilbert—Huang transform［J］.Math.Comput Simul，2005，70(1):22－32.

［5］赵进平.异常事件对EMD方法的影响及其解决方法研究［J］.青岛海洋大学学报，2001，31(6):805－814.ZHAO Jinping.Study on the effects of abnormal events to empiricalmode decompositionmethod and the removalmethod for abnormal signal［J］.Journal of Ocean University of Qingdao，2001，3l(6):805－814.

［6］张海如，王国富，张法全，等.改进的随机共振和EMD混合模型用于转子早期故障检测［J］.电机与控制学报，2014，(8): 84－89.ZHANG Hairu，WANG Guofu，ZHANG Faquan，et al.Conjoint model combining improved stochastic resonance and empirical mode decomposition for rotor incipient faults detection［J］.Electric Machines and Control，2014，18(2):84－89.

［7］WU Z，HUANG N E.Ensemble empiricalmode decompos-ition: a noise assisted data analysismethod［J］Adv.Adapt.Data Anal，2008，1(1):1－41.

［8］YEH JR，SHIEH JS，HUANG N E.Complementary ensemble empiricalmode decomposition:a novel noise enhanced data analysis method［J］.Advances in Adaptive Data Analysis，2010，2 (2):135－156.

［9］LILi，QU Liangsheng.Cyclic statistics in rolling bearing diagnosis ［J］.Journal of Sound and Vibration 2003，267(2):253－265.

［10］GAO Q，DUAN C，FAN H，et al.Rotatingmachine fault diagnosis using empirical mode decomposition［J］.Mechanical Sys-tems and Signal Processing，2008，22(5):1072－1081.

［11］LEIY，HE Z，ZIY.EEMDmethod and WNN for fault diagnosis of locomotive roller bearings［J］.Expert Systems with Applications，2011，38(6):7334－7341.

［12］CHANG K M，LIU S H.Gaussian noise filtering from ECG by Wiener filter and ensemble empirical moded ecomposition［J］.Journal of Signal Processing，2011，64(2):249－264.

［13］ZHANG J，YAN R，GAOR X，etal.Performance enhancement of ensemble empirical mode decomposition［J］.Mechanical Systems and Signal Processing，2010，24(7):2104－2123.

［14］王红军，万鹏.基于EEMD和小波包变换的早期故障敏感特征获取［J］.北京理工大学学报，2013，33(9):945－950.WANG Hongjun，WAN Peng.Sensitive features extraction of early faultbased on EEMD and WPT［J］.Transactions of Beijing Institute of Technology，2013，33(9):945－950.

［15］ZHOU Y，TAO T，MEI X，et al.Feed-axis gearbox condition monitoring using built-in position sensors and EEMDmethod［J］.Robotics and Computer—Integrated Manufacturing，2011，27 (4):785－793.

［16］LEIY，ZUO M J.Fault diagnosis of rotatingmachinery using an improved HHT based on EEMD and sensitive IMFs［J］.Measurement Science and Technology，2009，20(12):125701 －125712.

［17］窦东阳，赵英凯.集合经验模式分解在旋转机械故障诊断中的应用［J］.农业工程学报，2010，26(2):190－196.DOU Dongyang，ZHAO Yingkai.Application of ensemble empiricalmode decomposition in failure analysis of rotating machinery ［J］.Transactions of the CSAE，2013，32(8):63－67.

［18］PENG Z K，TSEPW，CHU F L.A comparison study of improved Hilbert-Huang transform and wavelet transform:application to fault diagnosis for rolling bearing［J］.Mechanical Systems and Signal Processing，2005，19(5):974－988.

(编辑:刘琳琳)

W ind turbine gearbox multi-fault diagnosis based on CM F-EEMD

WANG Zhi-jian，HAN Zhen-nan，NING Shao-hui，LIANG Peng-wei
(College of Mechanical Engineering，Taiyuan University of Technology，Taiyuan 030024，China)

Abstract:In view of the problems such as empiricalmode decomposition(EMD)modal aliasing phenomenon and ensemble empiricalmode decomposition(EEMD)precision which affected by the singularity of amplitude of the added white noise，an improved EEMD with combined mode function(CMF)was proposed.Combined mode function(CMF)was used as the pre-filter to improve EEMD decomposition results.CMF is combining the neighboring intrinsicmode functions(IMFs)which are obtained by EMD to get two new IMFs Chand CL.Chcontains high frequency components and CLcontains low frequency components.The proper added noise amplitude was determined according to the vibration characteristics to decompose Chand CLwith EEMD，and the purpose is that EEMD is further improved to increase the accuracy and effectiveness of its decomposition results.Finally，what extractsweak fault frequencymore effectively is cyclic autocorrelation function analysis for every characteristic IMF.The proposed method is applied to analyze themulti-fault of a wind power growth gearbox setup，and the results confirm the advantage of the proposed method over EEMD with cyclic autocorrelation function.

Keywords:wind gearbox;combined mode function;ensemble empirical mode decomposition;multifault;cyclic autocorr elation function

通讯作者:韩振南

作者简介:王志坚(1985—)，男，博士，讲师，研究方向为机械故障诊断;

基金项目:国家自然科学基金(50775157);山西省基础研究项目(2012011012－1);山西省高等学校留学回国人员科研资助项目(2011－12)

收稿日期:2014－10－09

中图分类号:TP 17;TP 206

文献标志码:A

文章编号:1007－449X(2016)02－0104－08

DOI:10.15938/j.emc.2016.02.015