基于自适应终端滑模控制的城轨列车精确停车算法

王青元，吴 鹏，冯晓云，张彦栋

(西南交通大学 电气工程学院，四川 成都 610031)

精确停车是城轨列车自动驾驶(ATO)系统的关键技术之一，其精度通常要求在±30 cm之内。精确停车能保证城轨交通系统的高效率运行。若列车停站不准确，不仅影响乘客的上下车，而且会造成列车晚点等诸多问题。因此，研究城轨列车精确停车算法具有重要意义[1]。

文献[2]设计模糊控制器，基于已知线路数据，实现有限离散级位下城轨列车的自动停车控制。文献[3]分析了城轨列车制动系统的构成特性，提出适合控制器设计的制动系统模型。该模型能够较好描述城轨列车制动系统的动态特性，并且基于该模型的自动停车控制系统在实验中也取得了满意的性能。基于此，文献[4，5]分别运用LQR和模糊PID控制，实现了列车在平直道的精确停车控制。但是上述控制器在设计的过程中，需要事先得知模型的准确参数，然而列车的设备包括制动系统等出现磨损和老化是不可避免的，这使得列车制动模型参数会发生变化。文献[6]引入了自适应控制，较好地克服了模型参数不确定性所带来的控制失准，但是其处理线路附加阻力的方式具有一定的局限性，面对线路变坡点时，切换过于频繁。在列车运行过程中，应尽可能的减少控制信号的切换，这样不仅降低制动系统设备的磨损，又能降低列车运行时的冲击度，提高旅客乘坐的舒适性。文献[7]为了克服自适应控制引起的控制输入频繁切换问题，进行了辅助系统的设计，平滑处理了变坡点的控制。该自适应控制算法虽然能使系统稳定，但当线路扰动较大时，列车运行状态收敛到要求的跟踪误差范围的快速性方面存在缺陷。文献[8]运用迭代学习控制对列车精确停车进行了研究，经过多次重复学习，列车最终可以克服运行环境的干扰，但是不断迭代的方式实时性较差。文献[9，10]将预测控制算法运用于停车控制器的设计，具有较好的鲁棒性，停车精度高。文献[11]在此基础上，引入参数估计以实现对列车制动系统模型参数的在线辨识，设计了自适应广义预测控制算法，其能较好地处理模型参数的不确定性和外部扰动。然而预测控制所采用的二次规划算法在求解过程中较为耗时，实时性方面不易保证。文献[12]通过引入应答器的数据，通过在线学习的方式对列车实施精确的控制，但是该算法依赖于应答器提供的数据。

自适应终端滑模控制因具有对系统内在参数扰动和外部干扰完全的自适应性、有限时间内收敛至平衡点等特点[13]，广泛应用于各种领域[14，15]。将线路断面引起的附加阻力和列车基本运行阻力以扰动形式引入滑模控制器，可有效减少对线路信息的获取，如线路坡道、线路曲线，并且对列车在明线或隧道内引起的扰动具有抑制作用。自适应终端滑模控制可在有限时间内收敛至平衡点，使得列车在停车过程中较快地跟踪参考曲线，能有效保证停车精度。本文通过对列车停车过程的分析，利用自适应终端滑模控制提出一种具有较强自适应性和鲁棒性的停车控制算法，并引入扰动观测器以进一步增强系统的抗干扰能力，以应对坡道较大线路所造成的附加干扰。通过仿真对所提出的算法进行了验证。

1 列车停车过程数学描述

1.1 列车牵引计算模型

列车在运行过程中受到线路附加阻力和基本阻力的干扰，可通过牵引力或制动力调整其运行工况。运动学方程可以表示为[16]

( 1 )

式中：M为列车的总质量，由列车自重和载荷质量组成，单位为t；γ为列车回转质量系数；v为列车的实时速度，单位为m/s；x为列车的距离，单位为m；F(t)为列车牵引力或者制动力，作为列车的控制输入；Rb(t)是基本运行阻力；Rc(t)是线路附加阻力，单位均为kN。假设列车的质量是均匀分布的。

基本运行阻力Rb(t)主要由空气阻力和机械阻力构成，可以表示为

Rb(t)=(r1+r2v+r3v2)Mg·10-3

( 2 )

式中：r1、r2和r3是阻力系数；g为重力加速度常数，m/s2。

列车基本运行阻力受环境因素影响，如风速、轨面情况等，工程中通过多次试验拟合获得各项系数，因此，模型中使用的公式在列车实际运行过程中不可避免地存在外部环境因素引起的扰动。

线路附加阻力Rc(t)主要包括坡道、曲线和隧道对列车所形成的线路阻力。

Rc(t)=(wi+wr+ws)Mg·10-3

( 3 )

式中：wi为单位坡道附加阻力；wr为单位曲线附加阻力；ws为单位隧道附加阻力。

为更加准确地计算线路附加阻力，引入多质点模型，如图1所示。即认为列车质量是根据列车长度均匀分布的，将整个列车视作均匀棒体，单位长度的质量相同。相比之下，利用单质点模型所计算出的附加阻力会出现明显的阻力阶跃跳变现象，而匀质棒模型的线路附加阻力相对缓和，使得模拟列车运行过程更贴近实际。

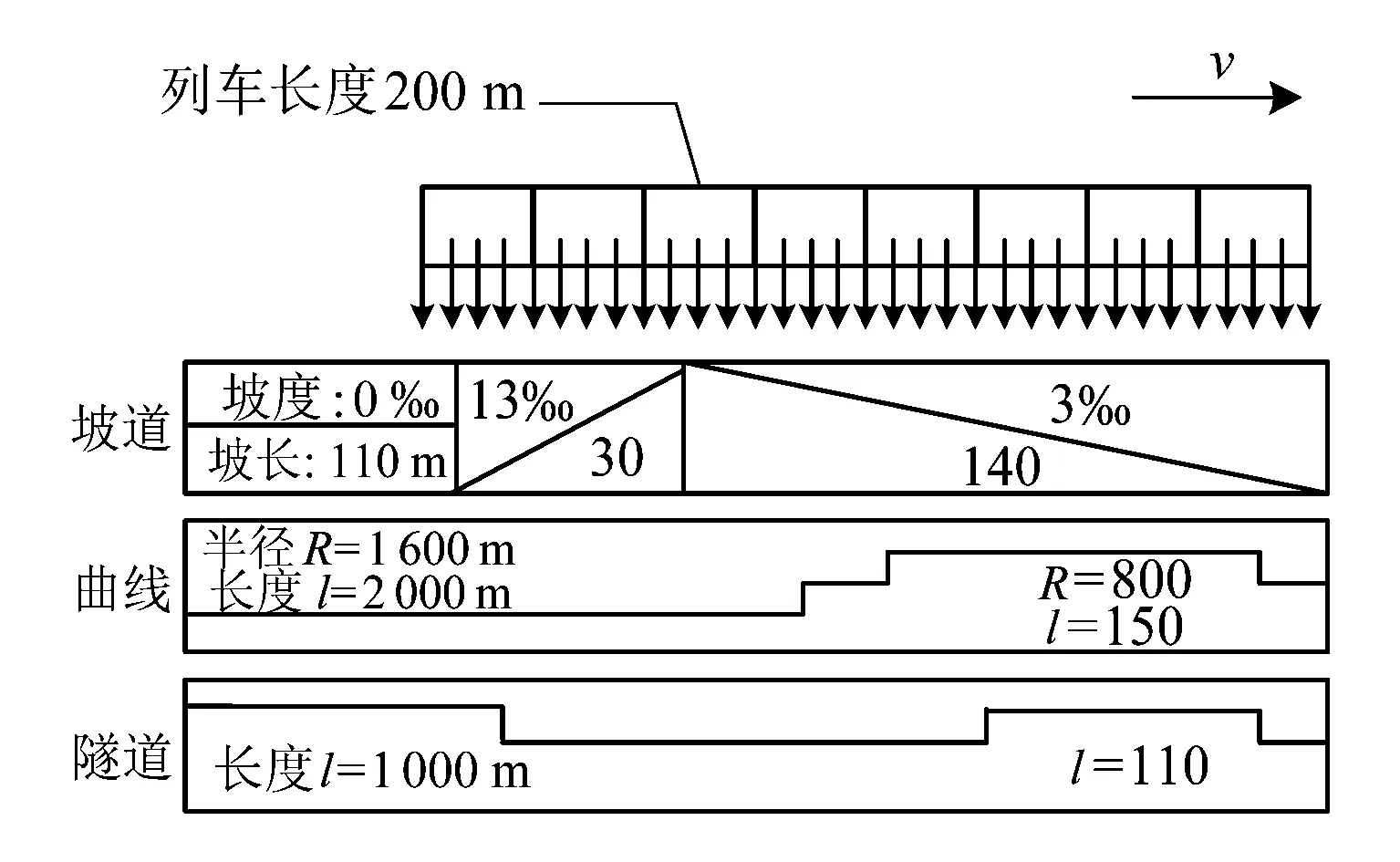
图1 匀质棒模型

1.2 列车制动系统

制动系统作为列车运行安全的基础保证，在需要减速的时候会对列车运行速度进行调整。现有城轨列车制动设备主要由电空联合制动系统构成，其通过调节列车电制动力和空气制动力的分配，以实施最终的制动。由于制动作用会受系统中机电装置传输延时的影响，其过程可被近似描述为典型工业过程中一阶滞后纯延时环节[3]。因此，制动系统的数学模型可以表示为

( 4 )

式中：ac为控制加速度，它是由制动控制器的作用产生的列车加速度；at为目标加速度，即ATO设定的列车制动加速度；τ为系统响应时间常数；Td为控制传输延时。

为了方便后续动力学关系描述，令

( 5 )

与此同时，由列车运行单位基本阻力和单位线路附加阻力构成的加速度可以表示为

d(t)=-W(t)-a-bv-cv2

( 6 )

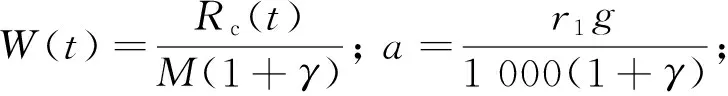
根据式( 6 )可得

( 7 )

既有城轨列车制动系统的控制运行方式多为无级制动模式[17]，因此设定列车制动系统为无级模式，则列车制动系统以及车辆动力学的模型框图如图2所示。

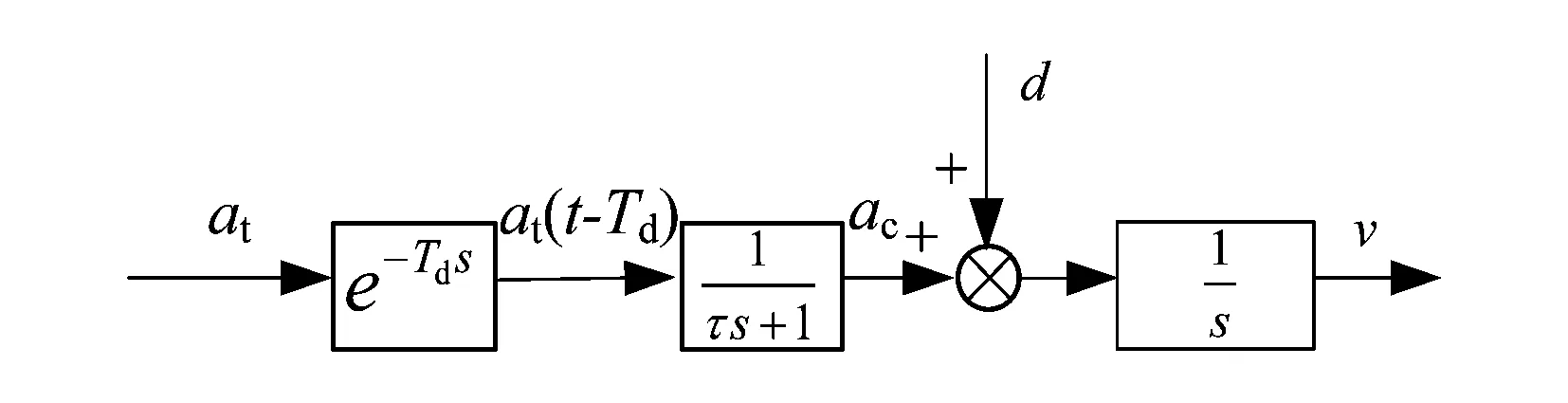
图2 制动系统模型

为方便后续控制器设计，采用pade逼近方法和拉普拉斯逆变换后可得

( 8 )

式中：λ为采用pade逼近方法时引入的与控制传输延时Td相关的常数，其与Td的关系表达式为

( 9 )

为便于表示，将式( 8 )表示为

(10)

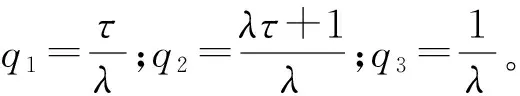
城轨列车停车过程采用一次制动方式，ATO系统将会实时跟踪停车制动曲线，完成精确停车[17]。停车的首要目标是实现高的停车精度，保持在±30 cm内。而且在整个停车过程中，需要对停车曲线保持较高精度的跟随性，并保证控制信号的平滑切换。

由图3可知，列车在开始进入停车模式之前，沿着ATO模式运行曲线进行速度跟踪控制。在进入停车模式后，由于制动系统的延迟因素，其对停车制动曲线的跟随性将会有一定时间上的滞后。但是，经过控制器的快速调整后，其可以快速地跟踪停车模式曲线，最终实现精确停车。在整个列车停车过程中，最大的控制难点在于对速度曲线的精确跟踪，因为较高的跟踪精度有利于保证后续停车位置的精确。然而，由于整个线路的坡道以及曲线的设计是由地势、车站分布、施工成本等因素综合决定，因此列车附加阻力具有较强的非线性。所以，如何有效克服线路附加的扰动是一个十分重要的研究目标。

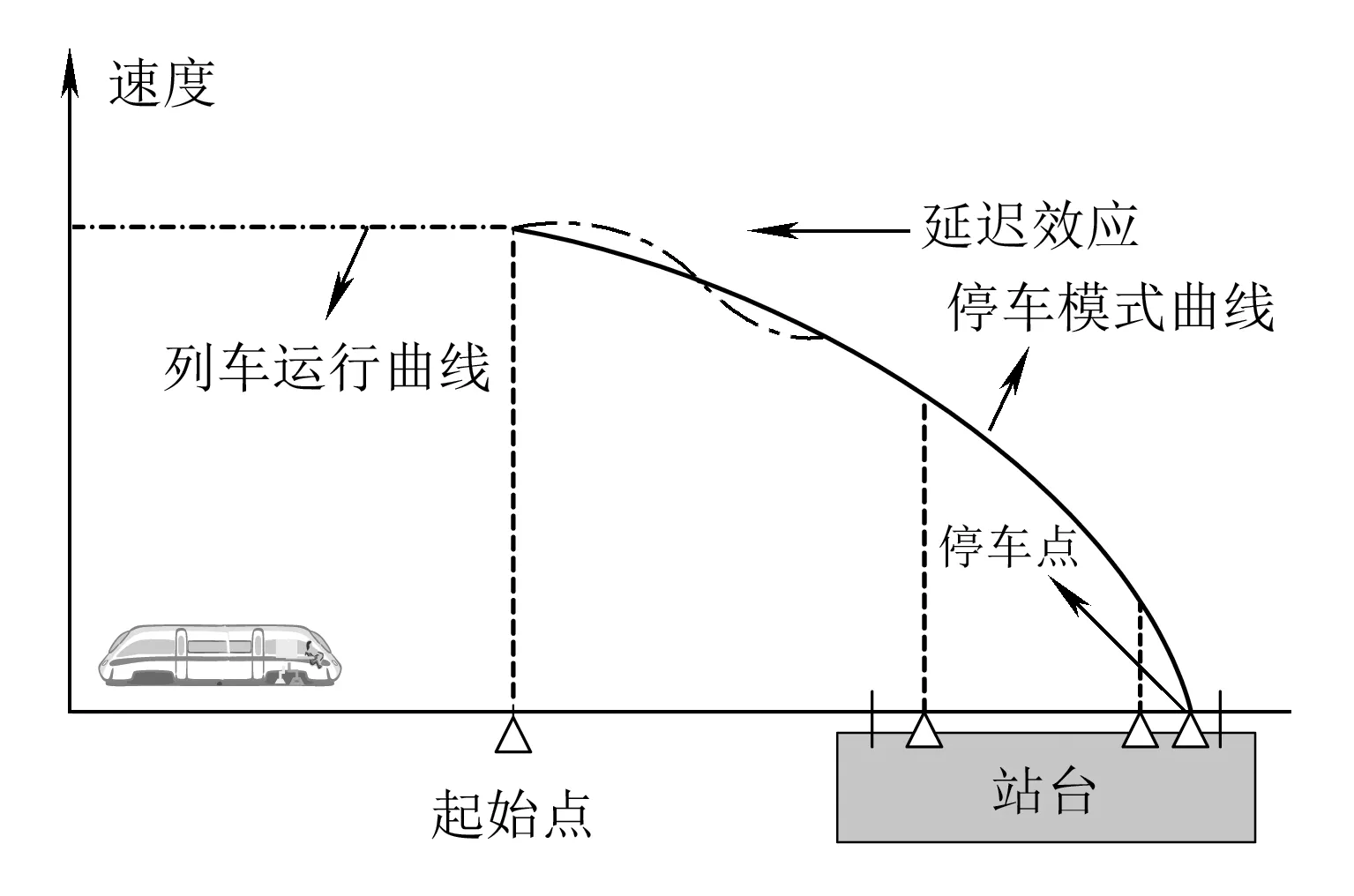
图3 制动系统模型

2 控制器设计

在整个列车停车过程中，对于控制器而言，其最大的控制难点在于对速度曲线的精确跟踪。其次，整个线路的坡道和曲线设计的复杂性决定了列车附加阻力的高度非线性。所以若控制器本身具有较好的扰动抑制能力，则在运行过程中的跟踪精度将得以保证，并有利于最终精确停车的实现。

由制动系统的工作流程可知，系统的延时参数等可能受到外界影响或者因系统磨损产生慢时变性，因此列车制动系统的参数不确定性会对列车的稳定运行产生影响。所以在控制器的设计过程中需考虑系统模型参数的不确定性。

列车停车控制的结构框图如图4所示。所设计的控制器需具备良好的鲁棒性，使其能克服系统外界阻力的干扰，并能克服制动系统参数的不确定性，从而实现稳定的在线控制，保证列车在停车过程中实现高精度速度跟踪、精确停车以及平滑控制输入等要求。

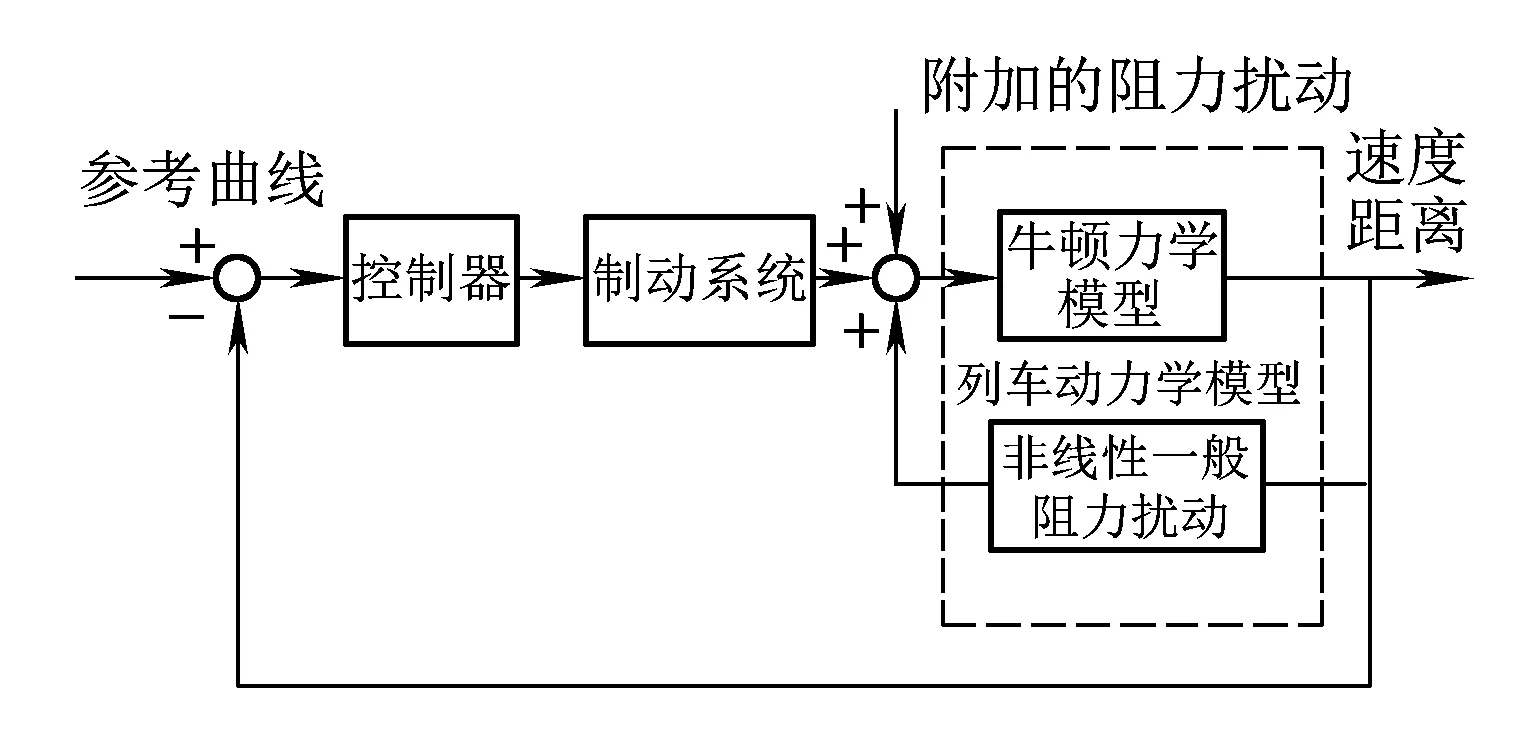
图4 控制器结构图

2.1 自适应终端滑模控制器

自适应终端滑模控制不仅具备很强的鲁棒性，而且可以使系统状态在有限的时间内收敛到期望的运行轨迹。另外其还具备较强的参数自适应处理功能，保证系统在具备参数不确定性时，不会出现不必要的不连续切换。

定义误差状态方程为

(11)

式中：e1为列车位置误差；e2为列车速度误差；xr为参考距离曲线；vr为参考速度曲线。将式(11)取微分代入到式( 7 )，可以得到新的误差状态空间方程为

(12)

在停车过程中，为满足准点要求，需要对参考距离和参考速度曲线实现精确的跟踪，因此设计的滑动超平面需要引入列车位置误差e1和列车速度误差e2，以保证误差的快速收敛。设计终端滑模函数为

(13)

式中：β>0；p和q为正奇数，而且满足1

下面将设计滑模控制器，实现对列车参考速度和参考位置的在线跟踪。

对滑模函数(13)求导可得

(14)

与此同时，由式( 6 )和式( 7 )可得

(15)

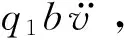
(16)

结合式(15)和式(16)，将式(16)带入到滑模函数的一阶导数(14)中有

(17)

基于滑膜控制器原理，滑模控制输入的形式为

u(t)=ueq+un

(18)

式中：ueq为系统的等效控制项；un为系统的非线性切换控制项。

令式(17)趋近于零可得

(19)

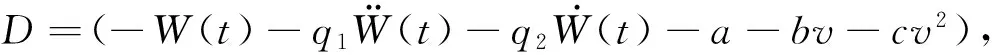
(20)

式中：k>0为控制增益。

又由于列车实际运行中列车的阻力项都是未知的，即D是未知的，但是D有界，因此实际的控制器应改为

(21)

式中：q4=q1c；q5=q2b；q6=q2c；且有k>Dmax。

选取如下形式的Lyapunov函数

(22)

令k0=k-Dmax，对式(22)求导并将控制器式(21)代入可得

(23)

则该系统稳定，且因切换项的存在能较好的克服运行过程中的扰动。但是为了增强鲁棒性，会增大切换项的控制负担，最终增加控制系统发生抖振的可能性。因此，基于自适应终端滑模控制理论，引入参数自适应机制。首先将控制器修正为

(24)

构造如下Lyapunov函数

(25)

式中：λi>0(i=1，2，…，9)为相应参数的自适应增益。

将式(25)进行求导可得

(26)

其中

将式(24)代入式(26)，有

(27)

为满足Lyapunov稳定性，对式(27)进一步整理可得参数自适应律为

(28)

根据上述所设计出来的自适应终端滑模控制律，因为其中不连续切换函数ksgn(sm)的存在，必将导致ATO系统发出不连续的控制信号，以保持列车的运行状态在滑模面上。但是列车在实际运行过程中，会由于线路附加阻力、基本运行阻力或者测量偏差等因素使得列车的运行状态无法停留在滑模面上，而使得状态误差在理想的滑模面上进行反复地穿越，最终形成抖振现象[18]。为避免过度的抖振以导致列车运行控制输入的频繁切换，将式(24)控制切换项中的符号函数sgn(sm)替换为饱和函数sat(sm)，φ为饱和宽度。

(29)

2.2 扰动观测器

饱和函数的引入必将降低系统的鲁棒性，然而列车在运行过程中所受到线路干扰可能较大，特别是坡度较大的线路条件下，会造成列车停车不精确等问题。因此，引入扰动观测器以增强系统的抗干扰能力。

考虑控制器式(24)，引入扰动观测值，将式(24)转变为

(30)

设计如图5所示结构的扰动观测器。

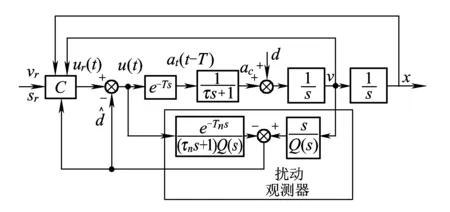
图5 扰动观测器结构图

由图5可知，实际模型和名义模型分别为

(31)

根据图5设计的扰动观测器的原理，考虑输入项为ur和d的传递函数，可得

(32)

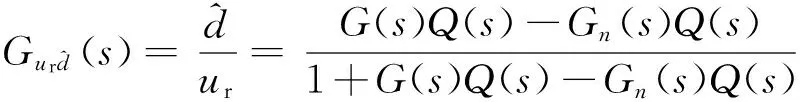
(33)

由式(32)和式(33)可得扰动观测值的表达式为

(34)

由式(34)可知，如果有Gn(s)=G(s)，则可以精确地观测出所需要的扰动值，但是在实际系统中，Gn(s)与G(s)之间可能存在偏差。由式(34)可分析出，估计值的偏差主要来自于模型的误差。

(35)

式中：ΔG(s)=Gn(s)-G(s)。Q(s)为低通滤波器，Q(s)=1。

由式(35)可知，如果模型存在偏差，所得到的观测器值也一定会存在偏差，模型误差大小决定观测值偏差的大小。引入扰动观测器后，将会在一定程度上削弱切换函数的增益。由于列车制动系统的参数是制动系统老化造成，其参数漂移是属于慢时变的，因此系统的模型误差一般相对较小。所以，引入扰动观测器能提高控制系统的抗干扰能力，且能降低切换增益，以避免抖振的产生。

3 仿真分析

分别对比不带扰动观测器的自适应终端滑模控制器(ATSMC)和带扰动观测器的自适应终端滑模控制器(ATSMC+DOB)的控制效果，考虑仿真线路为坡度较大的停车线路，如图6所示。车辆参数及其控制参数见表1和表2。考虑扰动观测器在设计过程中使用的模型参数具有20%的误差，同时，设计扰动观测器的低通滤波器的时间常数为0.05，阶次为3次。

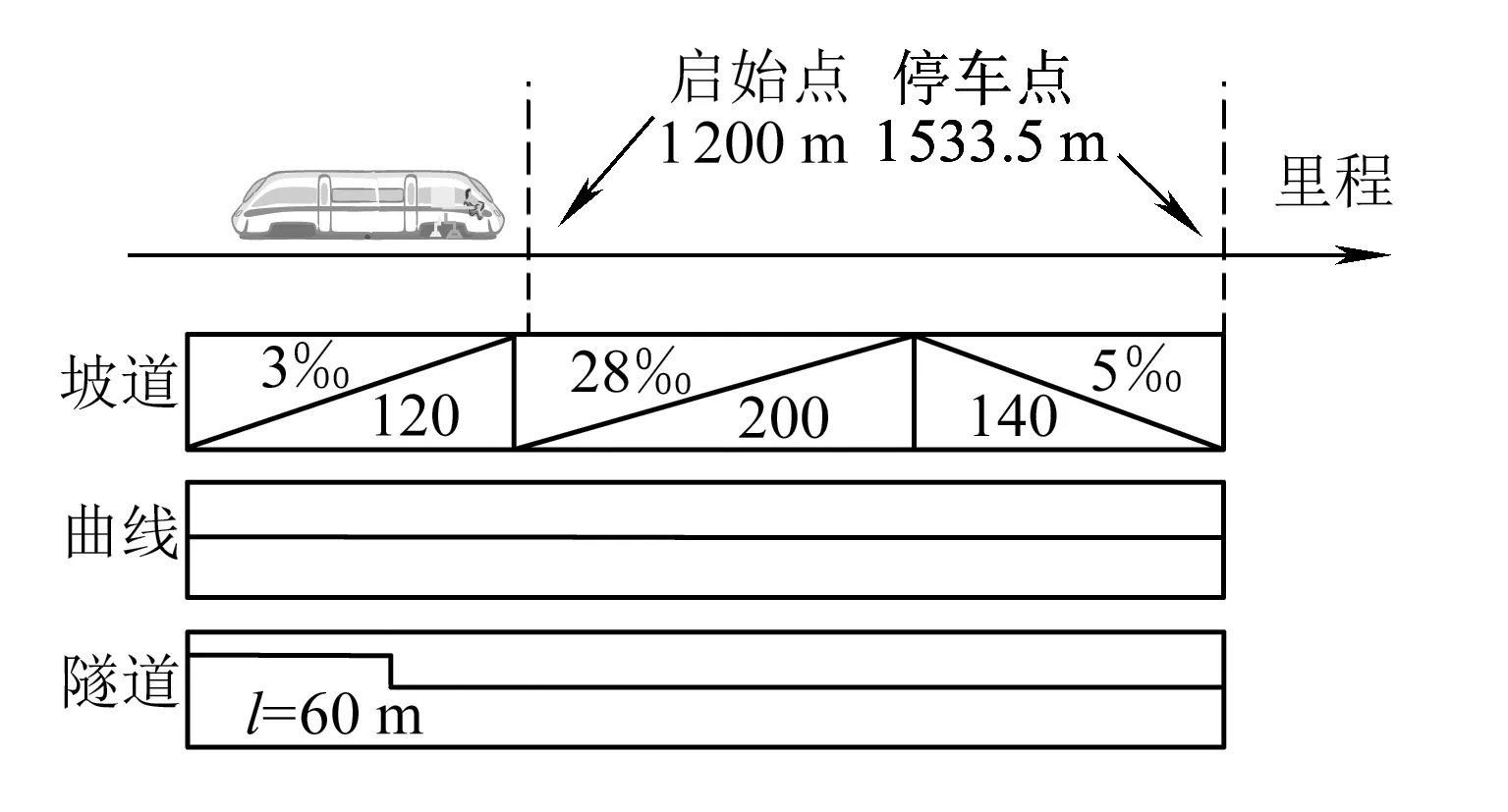
图6 坡度较大的线路条件图

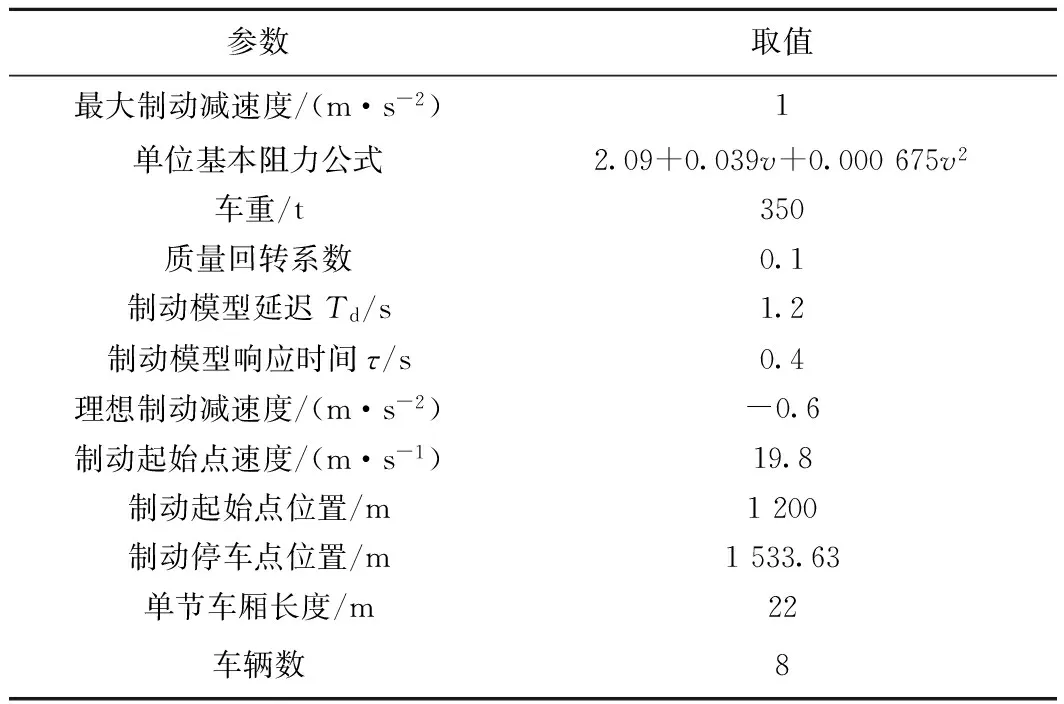
参数取值最大制动减速度/(m·s-2)1单位基本阻力公式2.09+0.039v+0.000675v2车重/t350质量回转系数0.1制动模型延迟Td/s1.2制动模型响应时间τ/s0.4理想制动减速度/(m·s-2)-0.6制动起始点速度/(m·s-1)19.8制动起始点位置/m1200制动停车点位置/m1533.63单节车厢长度/m22车辆数8

表2 列车运行基本参数

如图7所示，当列车运行在坡度较大的线路上时，由于外界干扰较强，导致自适应终端滑模控制器的控制精度下降，而为了克服外界的扰动，控制器在1 320～1 370 m处增强了不连续的非线性切换控制以维持控制的精度，如图8所示。但是频繁切换导致列车运行的舒适性降低，并且增大了制动系统的磨损。由于外界干扰较强，最终使得列车停车精度变低，停车误差为61 cm，并未满足精确停车的要求。基于扰动观测器的自适应终端滑模控制的仿真结果如图9所示，其不仅保证了列车在坡度较大的线路上的稳定运行，而且最终的停车精度为15 cm,达到了要求。因为引入扰动观测器，降低了不连续切换的可能性，使得列车停车全程过程中，并未出现图8所示的控制输入不断切换的现象，一定程度上提高了列车运行的舒适性，如图10所示。

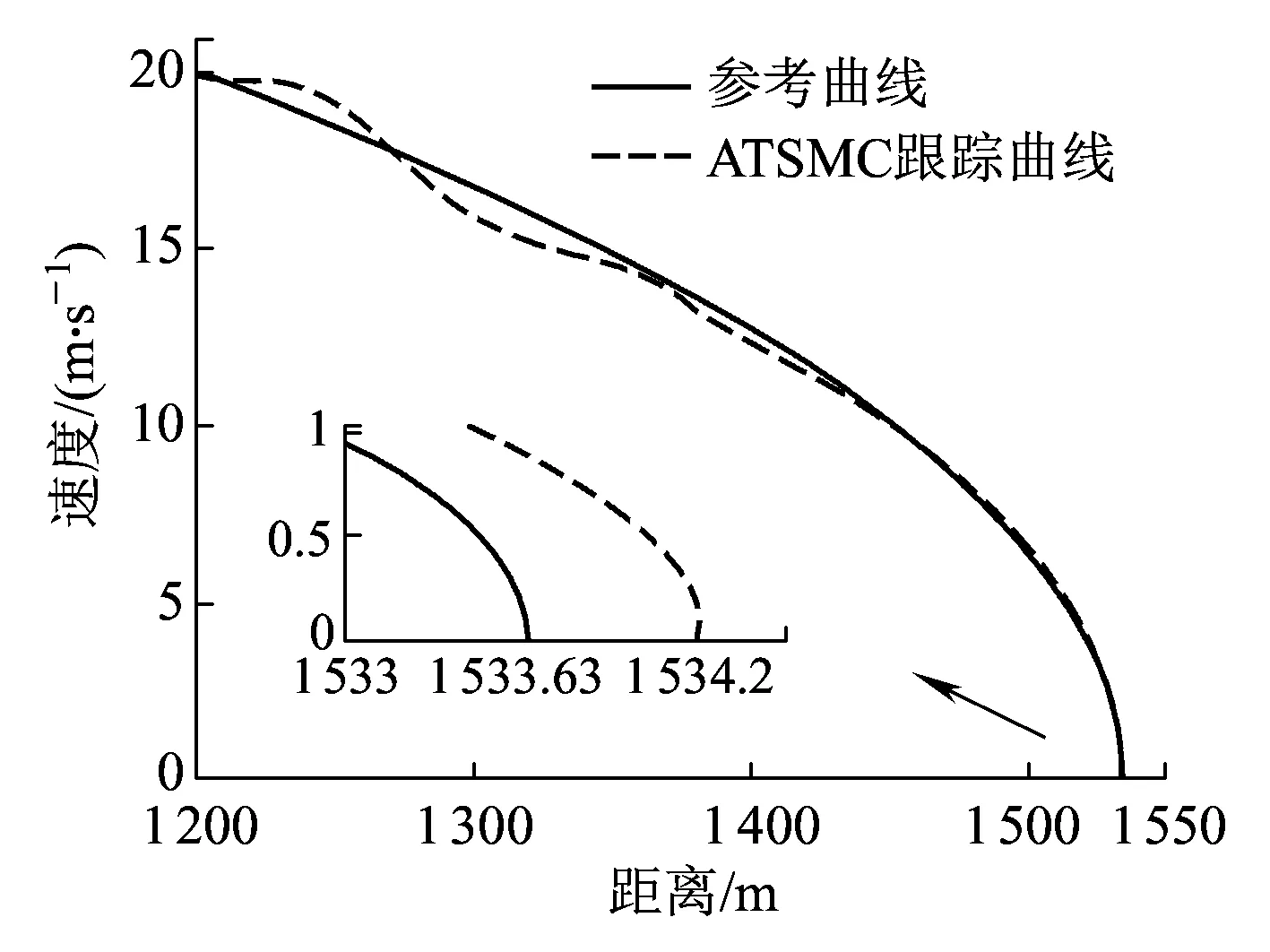
图7 ATSMC停车控制结果

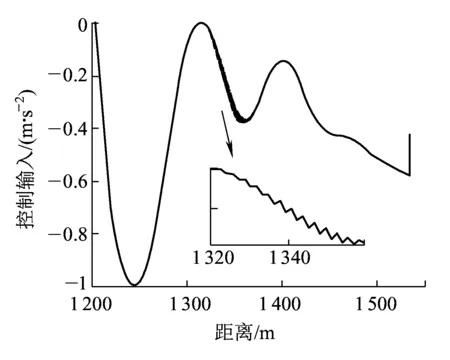
图8 ATSMC控制信号

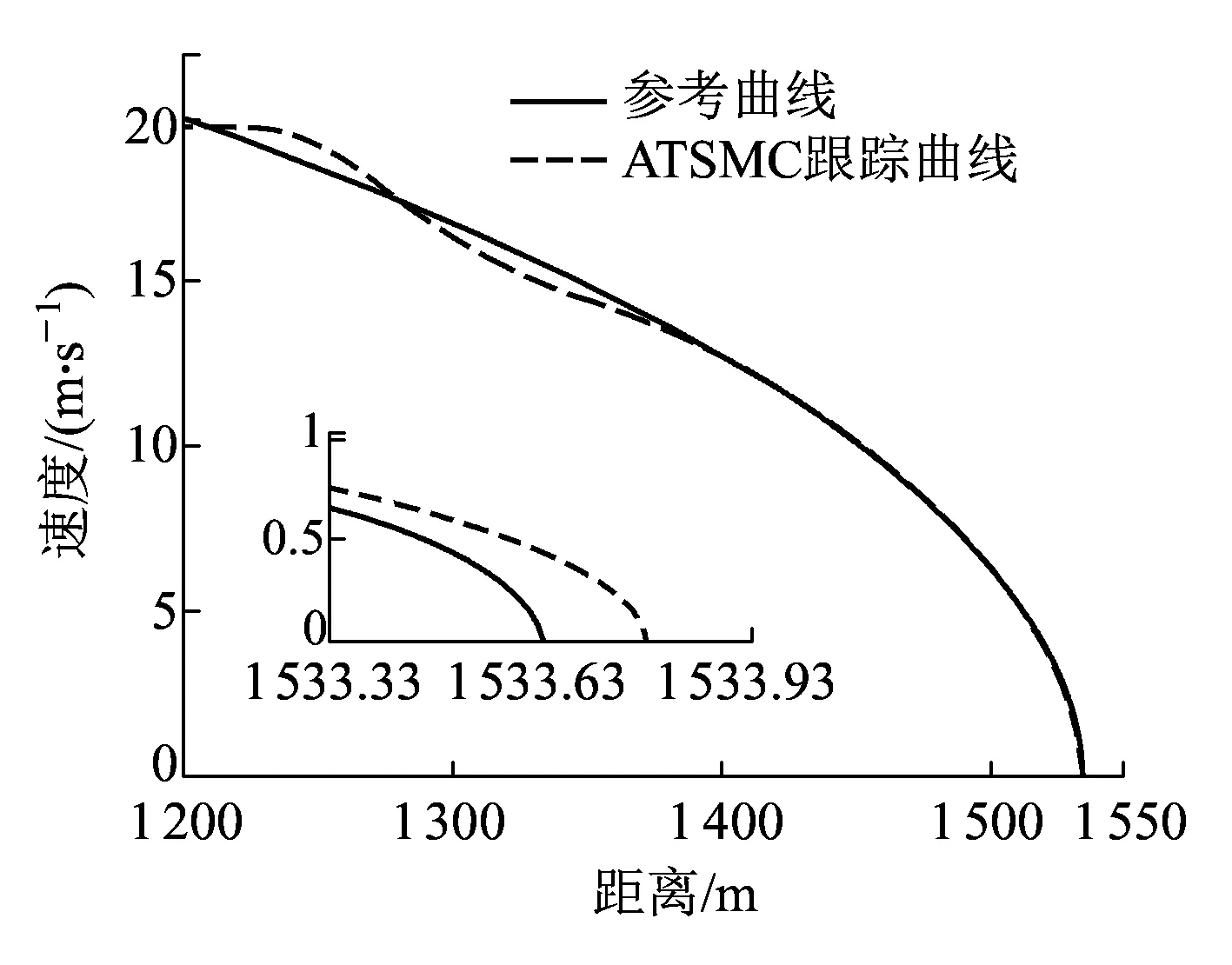
图9 ATSMC+DOB停车控制结果

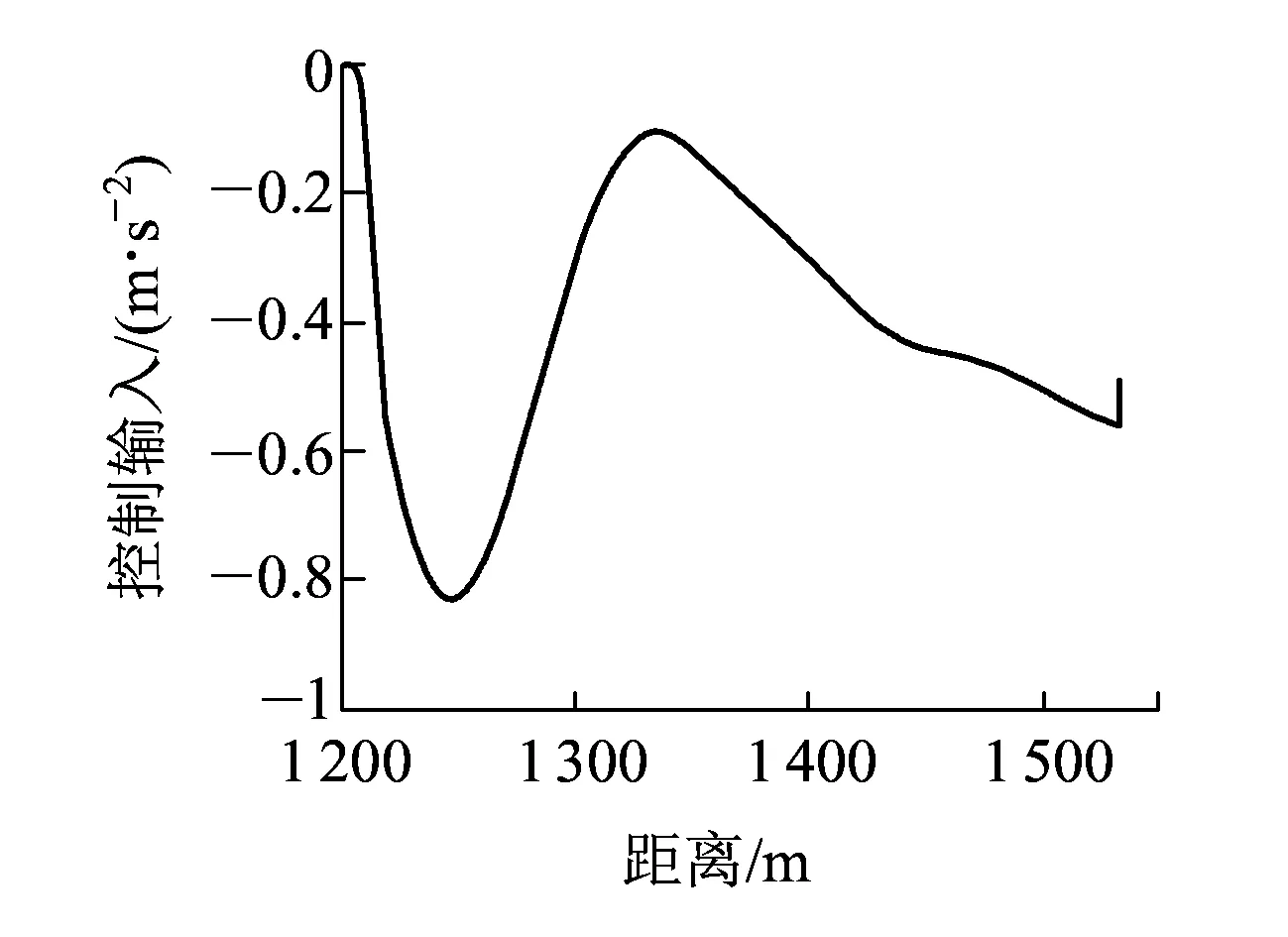
图10 ATSMC+DOB控制信号

如图11和图12所示，自适应终端滑模控制在面对较大外部干扰时，其状态误差收敛较慢，即列车的距离误差和速度误差整个过程偏差也较大。而基于扰动观测器的自适应终端滑模控制器在面对较大外部干扰时，调整速度较快，整个过程状态误差收敛较快，表现出较强的抗扰动能力。

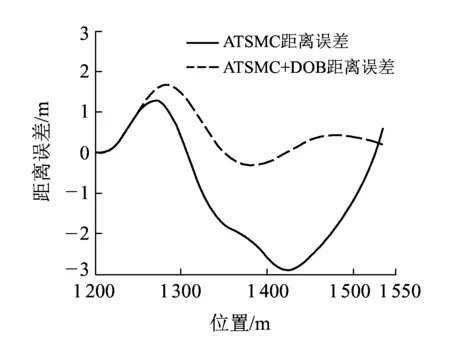
图11 停车过程距离误差

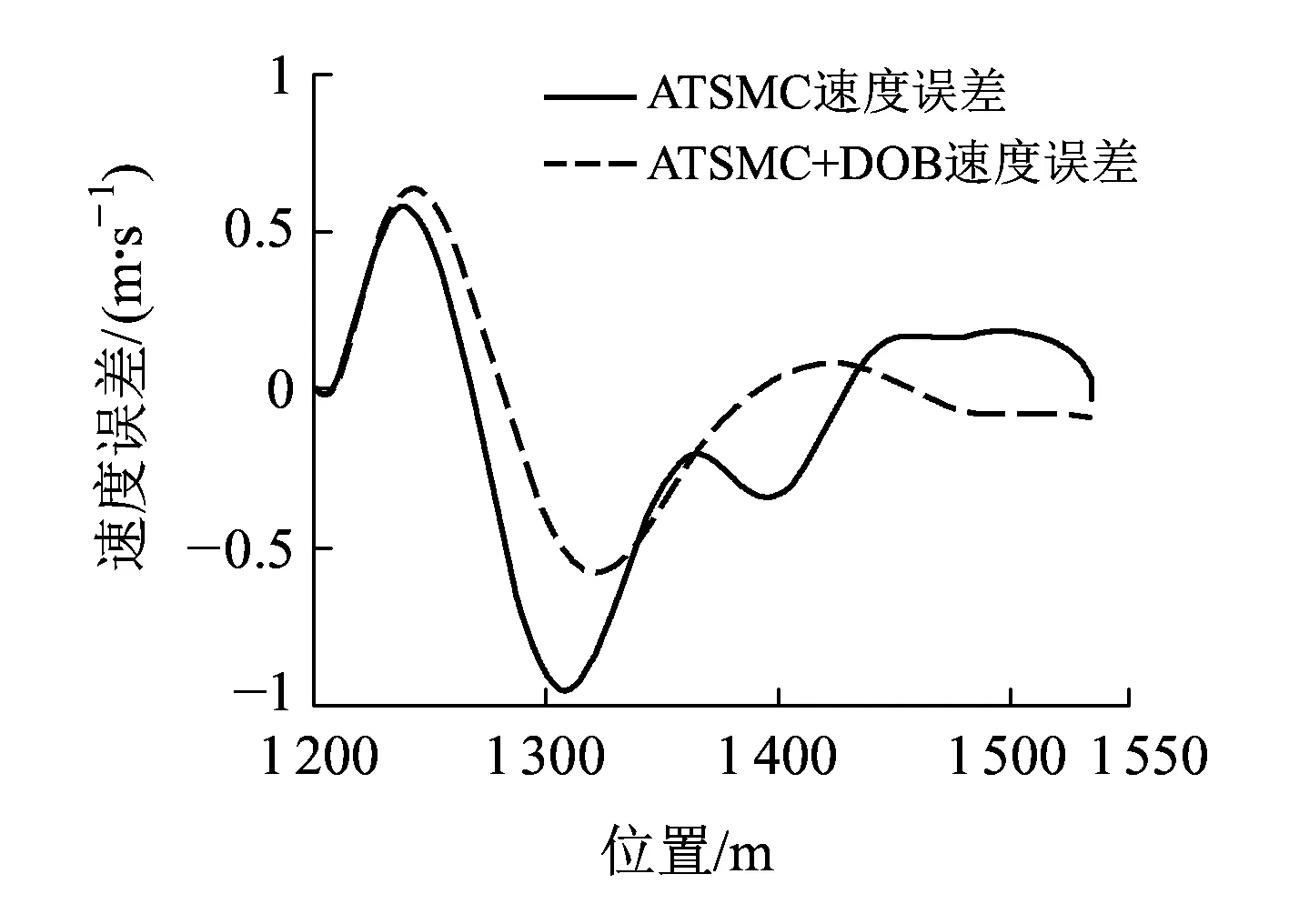
图12 停车过程速度误差

为进一步探讨基于扰动观测器的自适应终端滑模控制器的性能，分别对比基于不同制动系统模型误差ΔG(s)所设计出的扰动观测器的控制效果。

图13为不同模型误差下的扰动观测结果，当系统模型误差较小为20%或者无误差时，扰动估计较为准确。而当模型误差较大为50%，扰动估计值偏差较大。图14为不同模型误差下列车距离误差结果，当模型误差较小或者无误差时，因为观测结果较为准确，控制效果较好，停车过程中距离偏差收敛较快，最终停车精度得到保证，在±30 cm内。而当系统模型误差较大时，由于扰动误差较大导致列车距离误差无法实现收敛，最终无法实现精确停车，停车精度为±80 cm。

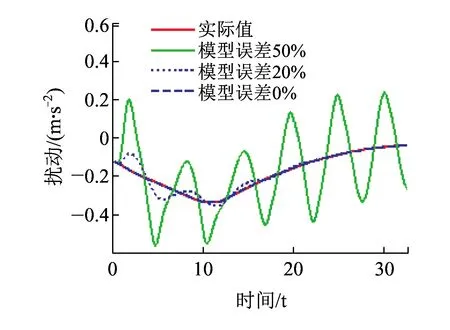
图13 不同模型误差下的扰动估计值

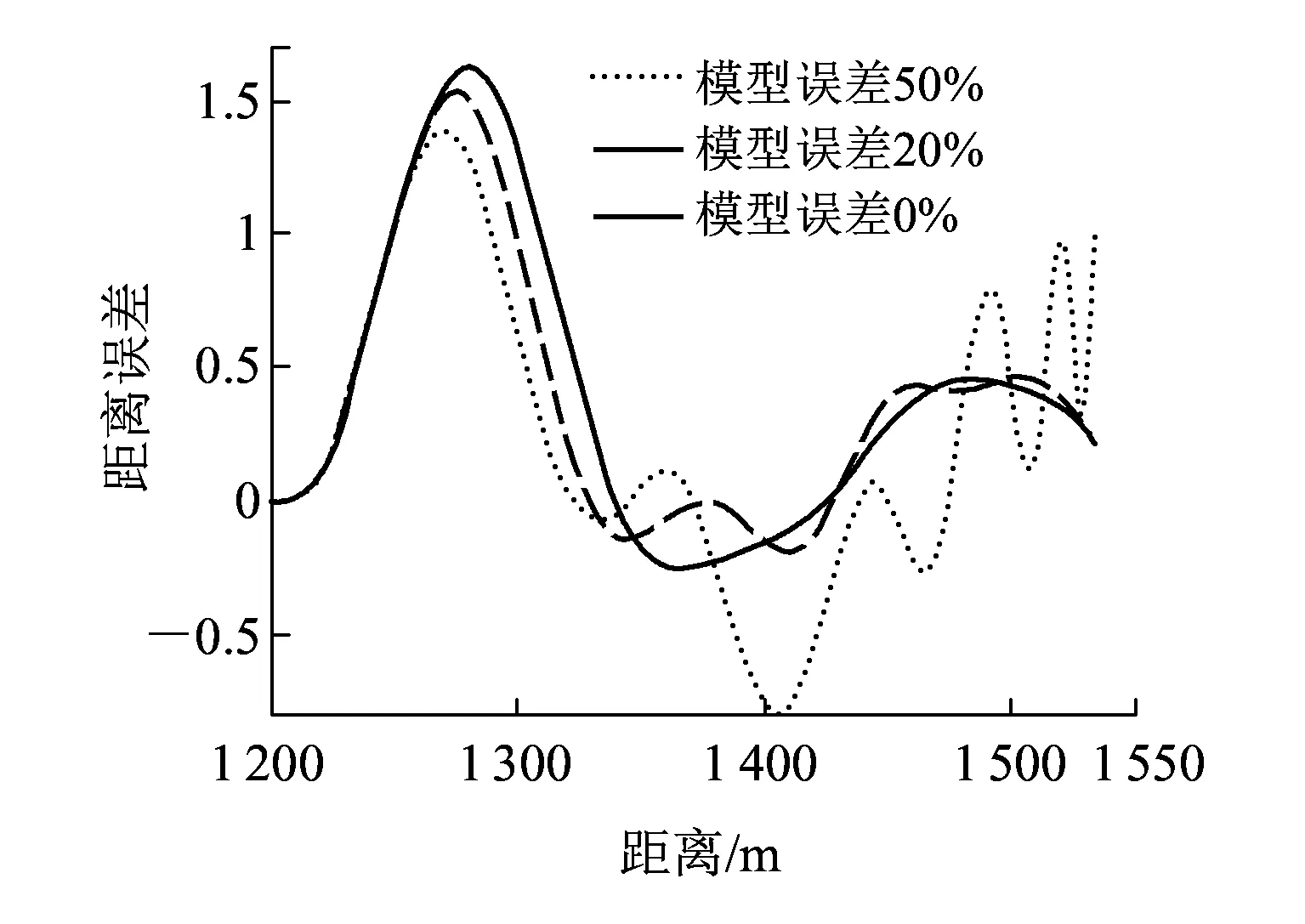
图14 不同模型误差下的停车过程距离误差

通过上述分析，模型误差在一定程度上影响了停车控制算法的性能。但列车制动系统参数主要变化是由于磨损老化导致，属于慢时变，在一定程度上系统模型误差较小，因此所提出的算法能满足运行的要求，具有普遍适用性。

4 结论

本文以城轨列车自动驾驶系统为研究对象，针对城轨列车精确停车算法进行了深入研究。结合列车制动系统模型，给出了列车停车过程的数学描述。基于列车精确停车的目标，提出了停车控制器设计的主要性能指标。针对列车自动驾驶中的精确停车技术，提出了自适应终端滑模控制器。利用终端滑模控制设计停车控制算法，以增强控制系统自适应性为目的，引入参数自适应机制，并通过仿真验证了算法的有效性。在自适应终端滑模控制停车算法框架的基础上，设计扰动观测器，并将扰动观测器的观测值引入到了控制算法的估计项中，增强了系统的鲁棒性和抗扰动能力。仿真平台对所提出的停车控制算法进行了全面的验证。当模型具有参数不确定性和外部扰动较强时，所提出的控制算法可以保证列车运行精确停车，同时平滑了控制输入，避免频繁切换。但当模型误差达到50%时，停站精度未得到保证，后续将作进一步研究。

参考文献：

[1]NING B,TANG T,GAO Z Y,et al.Intelligent Railway Systems in China[J].Intelligent Transportation System,2006,21(5):80-83.

[2]YASUNOBU S,MIYAMOTO S,IHARA H.A Fuzzy Control for Train Automatic Stop Control[J].Transactions of the Society of Instrument and Control Engineers,2002,2(1):1-9.

[3]于振宇,陈德旺.城轨列车制动模型及参数辨识[J].铁道学报,2011,33(10):37-40.

YU Zhenyu,CHEN Dewang.Modeling and System Identification of the Braking System of Urban Rail Vehicles[J]. Journal of the China Railway Society,2011,33(10):37-40.

[4]贺广宇.基于LQR的列车精确停车控制算法研究[D].北京:北京交通大学,2009.

[5]赵东旭,董昱.CTCS-2级列控系统ATO精确停车功能的研究[D].兰州:兰州交通大学,2012.

[6]罗仁士,王义惠,于振宇,等.城轨列车自适应精确停车控制算法研究[J].铁道学报,2012,34(4):64-68.

LUO Renshi,WANG Yihui,YU Zhenyu,et al.Adaptive Stopping Control of Urban Rail Vehicle[J].Journal of the China Railway Society,2012,34(4): 64-68.

[7]罗恒钰,徐洪泽.基于参考模型的ATO自适应控制算法研究[J].铁道学报.2013,35(7):69-73.

LUO Hengyu,XU Hongze.Study on Model Reference Adaptive Control of ATO Systems[J]. Journal of the China Railway Society,2013,35(7):69-73.

[8]王呈,唐涛,罗仁士.列车自动驾驶迭代学习控制研究[J].铁道学报,2013,35(3):49-52.

WANG Cheng,TANG Tao,LUO Renshi.Study on Iterative Learning Control in Automatic Train Operation[J].Journal of the China Railway Society,2013,35(3):49-52.

[9]王义惠,罗仁士,于振宇,等.考虑ATP限速的ATO控制算法研究[J].铁道学报,2012,34(5):59-64.

WANG Yihui,LUO Renshi,YU Zhenyu,et al.Study on ATO Control Algorithm with Consideration of ATP Speed Limits[J].Journal of the China Railway Society,2012,34(5):59-64.

[10]吴鹏,王青元,梁志成,等.基于预测控制的列车精确停车算法研究[J].计算机应用,2013,33(12):3 600-3 603.

[11]WU P,WANG Q Y.Research of the Automatic Train Stop Control Based on Adaptive Generalized Predictive Control[C]//The 33rd Chinese Control Conference,2014:3 399-3 404.

[12]CHEN D W,CHEN R,LI Y D,et al.Online Learning Algorithms for Train AutomaticStop Control Using Precise Location Data of Balises[J].IEEE Trans.Intell.Transp.Syst.,2013,14(3):1 526-1 535.

[13]颜闽秀.几类控制的若干滑模控制问题研究及应用[D].沈阳：东北大学,2008.

[14]范金锁,张合新,张明宽,等.基于自适应二阶终端滑模的飞行器再入姿态控制[J].控制与决策,2012,27(3):403-407.

FAN Jinsuo,ZHANG Hexin,ZHANG Mingkuan,et al.Adaptive Second-order Terminal Sliding Mode Control for Aircraft Re-entry Attitude[J].Control and Decision,2012,27(3):403-407.

[15]李前国,姜长生,黄国勇.基于自适应模糊快速终端滑模控制的导弹自动驾驶仪设计[J].系统工程与电子技术,2007,29(10):1 690-1 694.

LI Qianguo,JIANG Changsheng,HUANG Guoyong.Missile Autopilot Design Based on Adaptive Fuzzy Fast Terminal Sliding Mode Control Method[J].Systems Engineering and Electronics,2007,29(10):1 690-1 694.

[16]孙中央.列车牵引计算实用教程[M].北京:中国铁道出版社,2005.

[17]王长林,林颖.列车运行控制技术[M].成都:西南交通大学出版社,2008:70-80.

[18]UTKIN V I,YOUNG K D.Methods for Constructing Discontinuity Plans in Multidimensional Variable Structure Systems[J].Automatic Remote Control,1979,13(1):1 466-1 470.