基于Markov决策过程的列控系统定量安全分析方法
周 果,赵会兵
(北京交通大学 电子信息工程学院,北京 100044)
安全分析是所有安全苛求系统开发的必要过程,是事前预示、控制风险和保障安全苛求系统安全性的有力手段。列控系统是典型的安全苛求系统,系统安全完整性等级要求为SIL4,随机失效完整性应满足标准中对SIL4等级的要求,即容许隐患率THR(Tolerant Hazard Rate)小于10-9/h[1]。对列控系统的安全分析包括定性安全分析和定量安全分析两项任务,定性分析主要是全面地寻找导致隐患(Hazard)发生的原因,定量分析主要是计算隐患发生的可能性。对列控系统的定量分析是本文关注的核心问题,定量分析的结果一方面是判断隐患控制措施有效性的标准,另一方面是帮助开发设计人员决策风险(Risk)可接受性的依据。
传统定量安全分析方法(如故障树分析(FTA)、故障模式影响和严重度分析(FMECA)、Markov链(MC))在对简单小规模系统进行安全分析时有较好的效果,得益于它们易于学习和理解的优点,自提出以来就被极大程度地推广。然而随着系统复杂度和规模的不断提升,传统安全分析方法已经不能满足基于计算机技术的列控系统安全分析的需求,依靠手工和单纯人的联想推理已不能得到可信的定量安全分析结果。例如FTA在描述系统失效行为的过程中,启发式地联想推理失效条件,形成逻辑门的输入和输出,在系统规模庞大或结构复杂的情况下,不仅会遗漏失效事件之间的顺序关系,也会遗漏某些可能的输入输出事件。FMECA在归纳遍历所有组成器件失效模式和影响的过程中,需要安全工程师对系统行为非常熟悉,并对失效影响作出准确判断,由于组成器件众多,工作量巨大,难免会遗漏和出错,最终导致定量分析结果不可信。MC方法在面对多对象并发系统建模时,手工获得全局状态和状态迁移几乎不可能,因此需要开发新的定量安全分析方法。
为了克服以上传统安全分析方法的不足,学界提出了基于模型的安全分析(Model Based Safety Analysis)[2],它是基于模型的系统工程(Model Based System Engineering)的重要组成部分,其核心意义在于让设计工程师和安全工程师共同使用统一的系统行为模型,以系统设计的正常功能模型为基础,使系统验证和安全分析结合的更为紧密,得到完整可信的安全分析结果。2005年美国明尼苏达大学JOSHI A等[2]首次提出基于Matlab/Simulink模型的安全分析方法。2007年BOZZANO M等[3]开发了基于故障注入和模型检验的安全分析工具NuSMV-SA/FSAP。2013年altarica3.0项目启动,目的是开发基于失效逻辑建模语言Altarica的安全分析一体化平台[4]。由于以上方法对模型行为信息的描述各有侧重并不统一,且尚处于研究阶段,本文结合基于模型安全分析的思想,应用Markov决策过程作为系统行为模型建模基础,以概率模型检验为安全分析基础,提出了基于综合行为模型CBM(Comprehensive Behaviour Model)的列控系统定量安全分析方法。
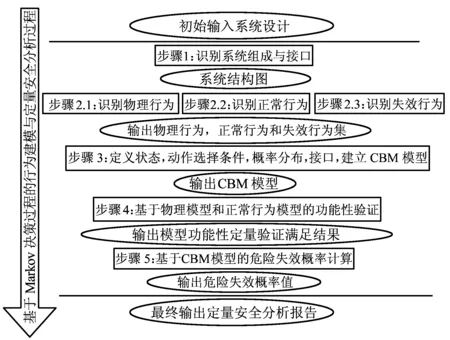
图1 基于Markov决策过程的行为建模与定量安全分析过程
该方法分为两个方面,综合行为模型的模块化建模和完整定量安全分析。图1为该方法的任务剖面,以系统设计作为输入开始,经过建模和分析两大过程最终输出定量安全分析报告。
1 建模与定量安全分析基础
1.1 基于模型的安全分析
基于模型的安全分析思想,一方面强调系统建模,认为模型准确真实地反映系统抽象属性是后续安全分析的基础,直接关系到安全分析结果的正确性;另一方面弱化分析过程,将分析过程交给自动化工具完成。要完整地描述定量安全分析关心的行为,需要包含以下5个方面:首先是物理行为,是指分析对象如列车在场景中实际运动的过程模型,是整个系统行为模型的基础;其次是正常行为,是指无失效前提下分析对象作为一个反应系统(Reactive System)对外界环境的响应控制逻辑;第三是失效行为,是指分析对象中可能出现的失效模式对应的行为模型;第四是不确定(Non-deterministic)行为,是指并发系统中下一步执行行为的选择是不确定的;第五是概率(Probabilistic)行为,是指一个行为的执行符合某种概率分布。将以上5种行为整合为一个行为模型,称为综合行为模型CBM 。
1.2 Markov决策过程
由以上5方面的建模需求,选择Markov决策过程MDP(Markov Decision Process)[5]作为建模基础,因其具有表达不确定行为和概率行为的双重能力,又能实现物理行为、正常行为和失效行为的并发建模,是其他建模工具如Petri网、Markov链等不能比拟的。另外,由于建模过程中,每一时间步内系统行为概率分布的确定并不依赖于之前历史状态的影响,只与当前状态有关,符合无记忆即马尔科夫性。基于以上理由,可以实现在统一的建模基础下完成CBM模型的建立。
首先给出Markov决策过程的形式定义。MDP是一个五元组。
M=(S,Act,P,s0,AP,L)
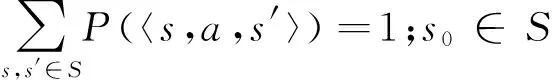
对于每个状态s∈S,MDP在每一时间步内至少选择一项不确定性动作a∈Act,并按该动作的概率分布执行。形式上每一步动作执行是一个有序对(ai,μi),其中ai∈Act且μi∈P,i∈N。MDP中一条完整的路径由一系列状态与动作组成,设一条无限路径为
式中:ai∈Act;μi∈P(si,ai+1,si+1)且μi>0,i≥0。设有限路径为
n∈N
它是无限路径π的前缀,终止状态为sn。对无线路径π或有限路径ρ而言,其第i个状态si记做π(i)或ρ(i),迹记做tr(π)=(a0,μ0)(a1,μ1)(a2,μ2)…或tr(ρ)=(a0,μ0)(a1,μ1)(a2,μ2)…(an,μn),由路径上的所有动作组成。如图2所示,圆表示状态,三角形表示动作,虚线有向弧表示动作的选择,实线有向弧表示概率状态迁移,虚线有向弧上标注的是触发该动作的条件,实线有向弧上的正实数表示动作概率分布中的该状态迁移的概率。
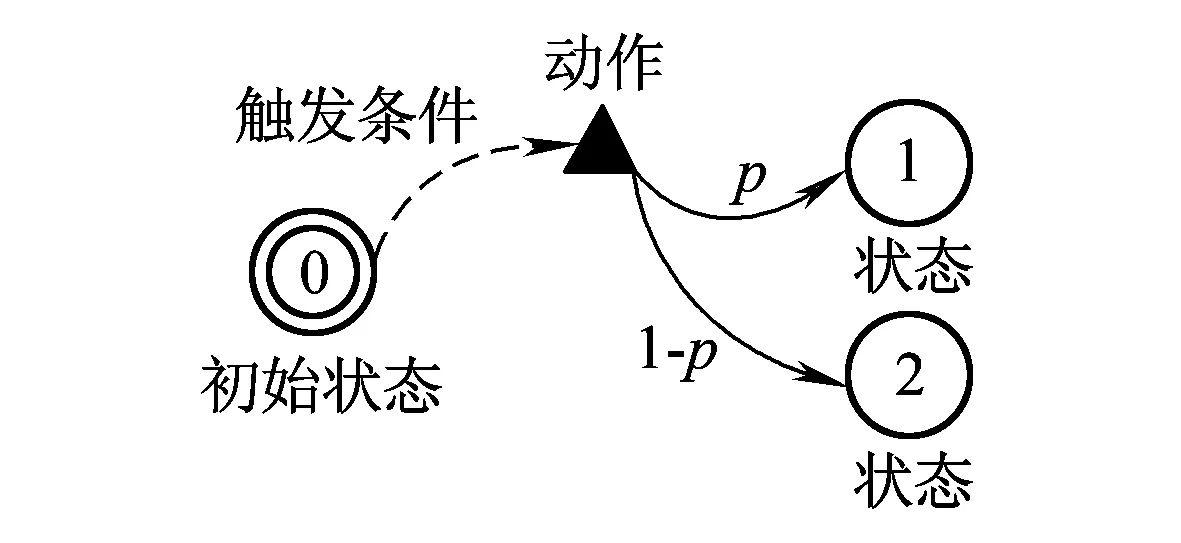
图2 MDP的图形表示
2 基于MDP的系统行为建模
2.1 基于MDP的物理行为建模
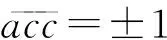
根据以上物理运动的设定,可建立列车物理运动的MDP模型,如图3所示。对列车位置和速度的生成是迭代进行的,两个物理量可选择的动作集Act中仅有一个叠加动作,即图3中的a1,表示同步地将下一时刻的速度增量Δv和位移增量Δl叠加到上一时刻的速度值v(t)和位移值l(t)上,得到下一时刻的速度值v(t+1)和位移值l(t+1),表示规则如式( 1 )所示。每次叠加动作完全叠加到上一时刻的值之上,所以对速度和位移两者单独来讲,动作a1以概率1到达下一状态。
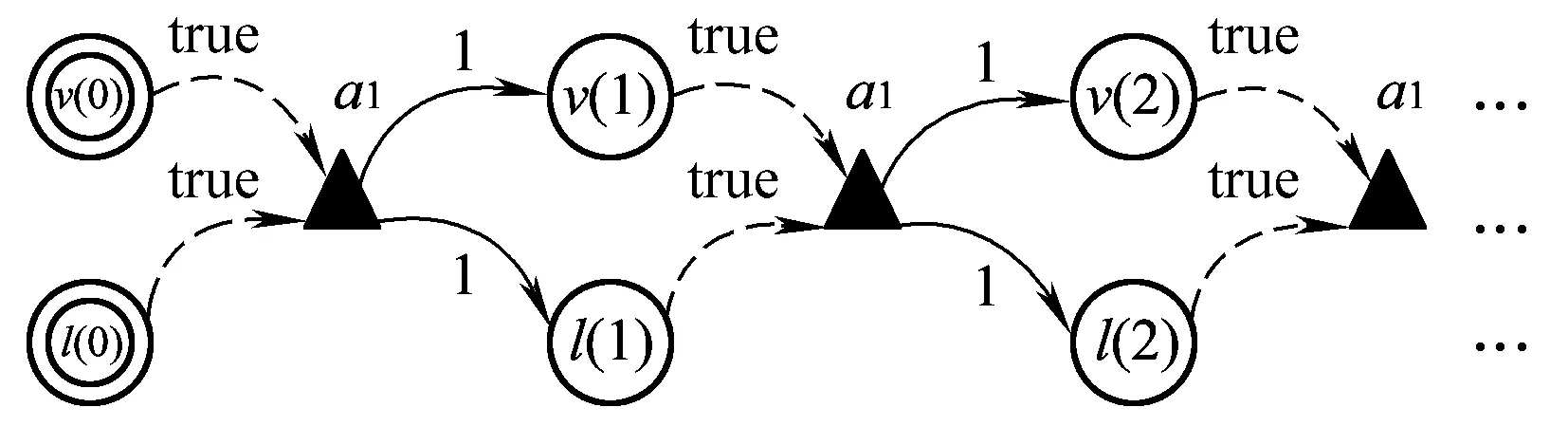
图3 列车物理运动模型
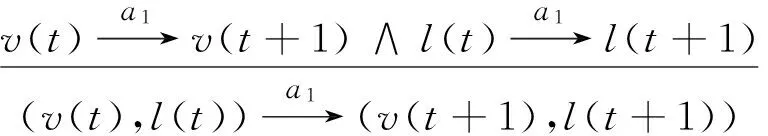
( 1 )
2.2 基于MDP正常行为的建模
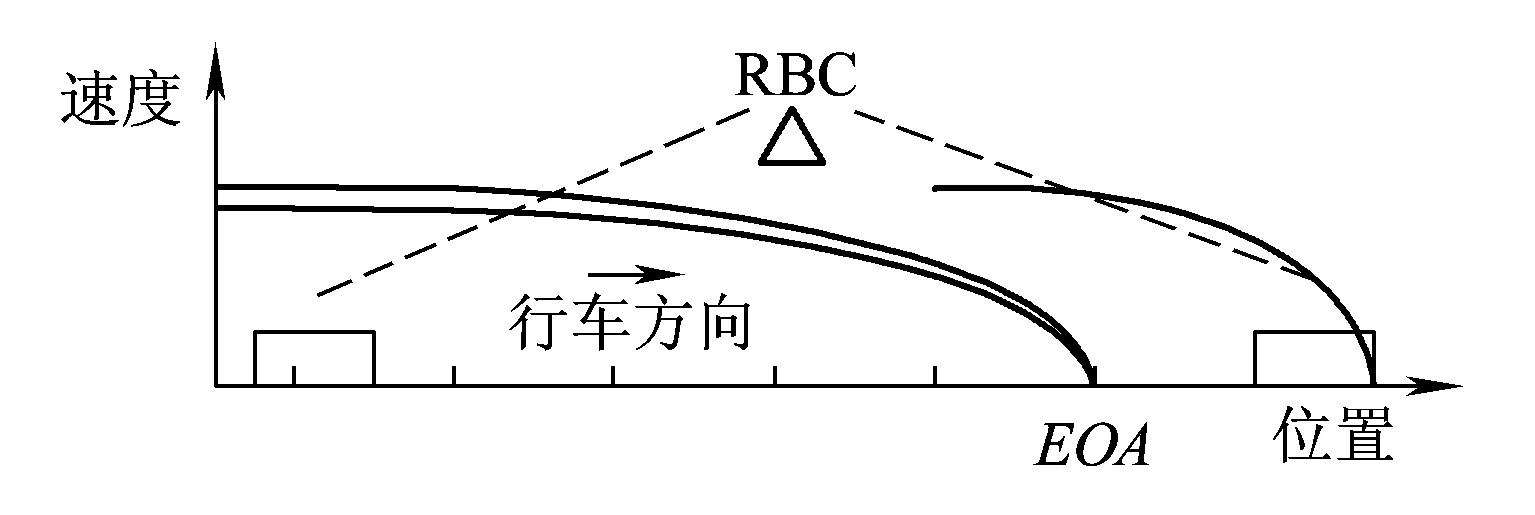
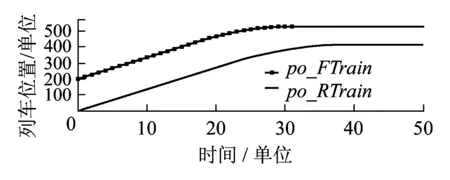
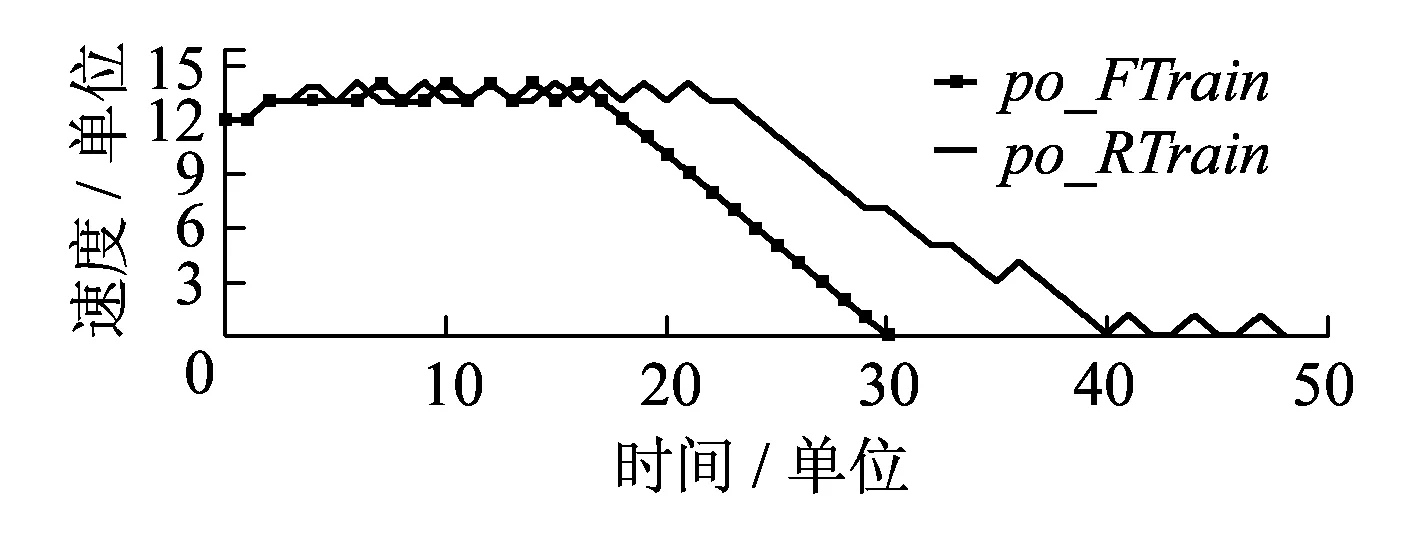
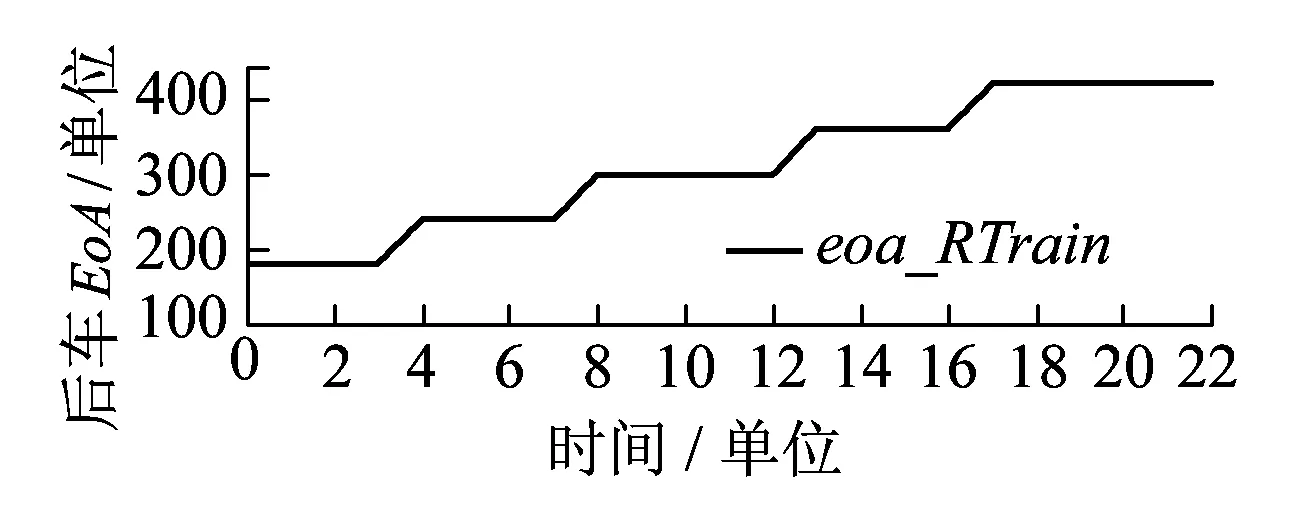
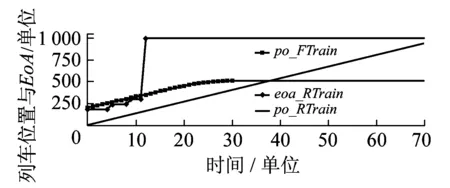
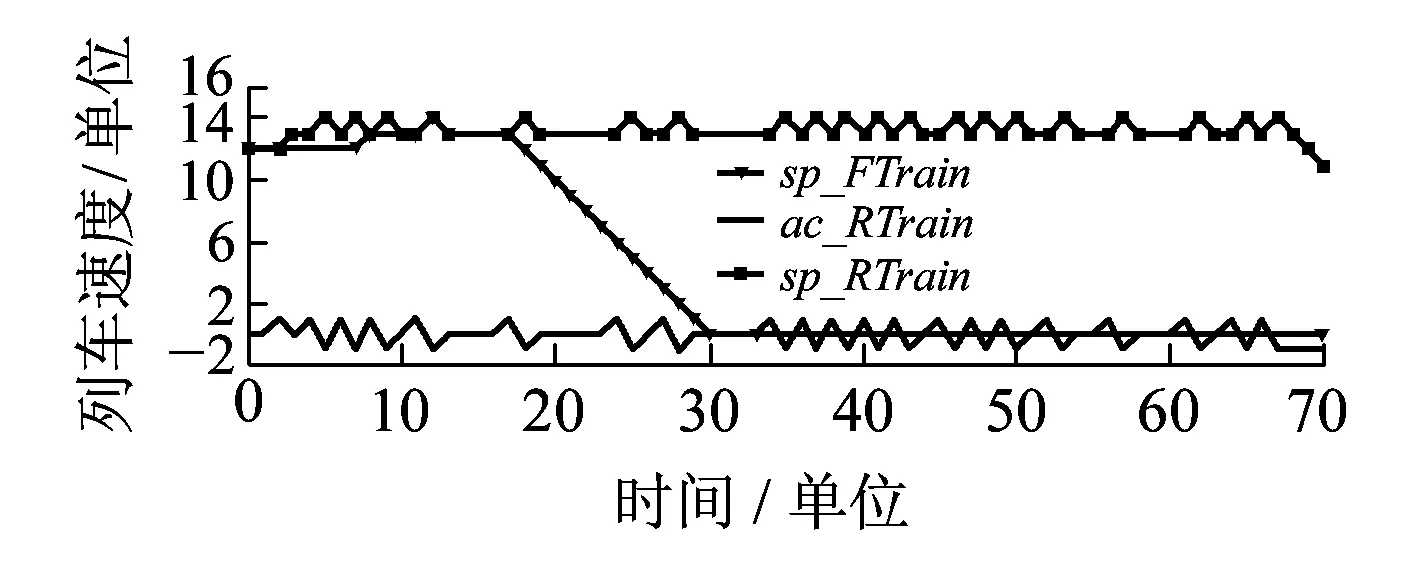
设列车制动触发值与限速值的速度差为vc,当下一刻的车速v(t+1)使得命题brake:v(t+1) 图4 列车正常行为模型 失效行为是指对象内部发生故障(Fault)后经过演变,在对象边界上使得表征功能的量产生错误(Error),最终导致对象所要实现的某种功能丧失即失效(Failure)的一系列过程。一个对象的失效行为模型也是一个MDP,可能包含不确定行为和概率行为。失效行为的组成根据失效可恢复性分为瞬态性失效和永久性失效两类。瞬态性失效指失效可在有限步时间内恢复到正常状态的失效模式,相反永久性失效指失效不能在有限步时间内恢复到正常状态的失效模式。根据失效触发的形式,失效行为可分为时间性失效和请求性失效两类。时间性失效指对象的失效过程是与时间相关的连续失效过程,而请求性失效指失效只在外界环境请求对象提供安全功能的时候发生。 这4种失效均可由MDP来进行建模。以列控系统中车载设备计算列车位置的安全功能为例,建立时间性瞬态失效模型;以RBC计算列车EoA为例,建立时间性永久失效模型;以车载设备与无线闭塞中心之间安全数据交互的安全功能为例,建立请求性瞬态失效模型;以列车请求制动的安全功能为例,建立请求性永久失效模型。4类失效行为的MDP模型如图5所示。模型5(a)和5(b)分别是车载设备故障导致的列车定位错误和RBC计算EoA错误,状态0和1分别表示未发生故障状态和发生故障状态;模型5(c)和5(d)分别表示车载设备与无线闭塞中心之间安全信息通信错误和车载设备请求制动失效,状态0、1和2分别表示初始状态、未发生故障状态和发生故障状态。请求性失效存在初始状态是由于对请求的响应需要一个时间步长,为了使失效正好发生在安全功能被请求的时刻而没有一个时间步长的延迟,增加了一个虚拟的初始请求,其触发条件始终为真,这使得在下一次请求到来时,保证失效模型只对其做出一次响应。 图5 4类失效行为模型 根据以上3部分的建模方法和模型修订规则,可建立列控系统中系统层面各实体的行为模型。为了得到完整统一的行为模型,需要将它们整合为综合行为模型CBM(Comprehensive Behaviour Model)。根据并发系统建模理论[5],定义两个并发的MDP模型M1和M2,其合成的MDP模型为 M=M1‖M2=(S,Act,P,s0,AP,L) 使得 M=(S1×S2,Act1∪Act2,P,AP1∪AP2,L) 定量安全分析的目的是计算系统隐患发生的可能性即危险失效概率或危险失效率,并判断它是否在可接受的概率风险范围之内。定量安全分析与定性安全分析相比,其优势在于它的值可作为设计人员比较和改进设计的参考指标,是设计人员按照定性安全分析结果对系统设计进行改进后的效果验证。基于以上理由,本文采取的基于模型的定量安全分析必须保证足够的正确性和完整性。正确性是指定量分析过程的确准确计算了导致隐患发生的一系列顺序事件的可能性,而完整性是指所有导致隐患发生情形的可能性都被计算在定量分析过程中。 为了满足正确性和完整性的要求,应用概率模型检验技术对CBM模型进行分析。概率模型检验技术确保对由CBM模型生成的状态空间进行遍历搜索,并对到达危险状态的所有路径的概率进行准确计算,同时现有的先进模型检验工具PRISM[6]可高效地处理大规模状态空间分析,且PRISM语言可方便地描述包含不确定行为和概率行为的MDP模型。 定量安全分析包括两类任务,基于系统正常行为的功能性验证和基于CBM模型的危险失效概率计算。首先,即使正常行为的功能性验证通过,证明了设计的安全功能可实现且危险状态不可达,也不能证明在系统中某个失效或多个失效发生时系统仍然是安全的。其次,只要存在失效,隐患永远不可避免会发生,定量分析的目的就是要确定各种失效情形出现的条件下,隐患发生的可能性被有效控制。因此,这两类任务中前者是后者的基础。 为了验证方法的有效性和先进性,选择列控系统区间运行中的双车追踪场景为例进行定量安全分析,首先对系统进行CBM建模。如图6所示,在CTCS3级列控系统中[8],线路情况与第2章中相同,两车初速度为12个速度单位,RBC将前车报告的位置信息和来自列控中心的轨道占用信息与联锁进路信息综合为移动授权信息MA,将移动授权终点EoA发送给后车,后车根据EoA、自身当前位置po(t)、速度sp(t)、加速度ac(t)(包括减速度SB)、列车车长Length400 m、安全保护距离SafeDistance100 m和静态限速Maxspeed等信息,计算当前限速速度sb和制动触发速度bt,保证列车前端在危险点前停车,由于系统采用固定闭塞模式,即危险点在前车停车时所在区间之后整数个区间的入口处。当前车在300个长度单位位置处发生紧急情况制动停车时,后车对危险点进行追踪,追踪间隔一个闭塞区间。本文主要研究RBC和后车ATP之间协作产生的失效,故假设前车、地面轨道电路和应答器等设备正常。 图6 CTCS3级双车追踪场景 本文采用PRISM工具对CBM模型进行建模和分析,PRISM工具[6]是由牛津大学开发的先进概率模型检验工具,PRISM语言是一种基于状态的反应系统形式的建模语言,支持包括Markov决策过程MDP在内的多种概率行为模型的建模和检验。语言遵循模块化的建模思路,对组件模块(Module)定义其局部状态变量(Local Variable)或全局状态变量(Global Variable),多个模块组合形成系统,系统全局状态由各模块的状态组合确定。模块的行为由一组命令(Command)组成,形式为 []guard->prob_1:update_1+…+ prob_n:update_n 式中:标记[]中表示该命令的名称用来控制命令的同步;guard为命令触发的条件;prob_n为状态转移概率;update_n表示状态更新。 图7 EoA计算PRISM表达式 RBC计算好后车的EoA之后,通过状态变量eoa_RTrain的更新将其发送给后车车载ATP,当eoa_RTrain的值在其初始值与设定线路长度Rail之间时,将值更新为下一时刻的eoa_RTrain值,供后车计算限速使用,其PRISM模型如图8所示。命令标记“[t]”被添加到每条命令之前,模拟时钟信息,使模型全局同步执行可执行的命令,eoa_RTrain′表示下一时刻的状态值。 图8 RBC控制发送EoA模型 自此,物理模型、正常行为和失效行为模型都已获得,根据2.4节中CBM模型合成规则,将失效模型注入到物理模型和正常行为模型中,由于规则已经详细描述,这里不再重复。 本文使用对属性规范语言概率计算树逻辑PCTL的检验来实现第3章中定义的定量安全分析任务。使用G(global)模态逻辑操作符表达属性,设ψ为MDP模型M上的一个路径表达式,πi是无限路径π的前缀,操作符G的定义为MMDP,πGψ⟺∀i≥0:MMDP,πiψ,表示对某条路径来说所有状态都使ψ成立。 第一步追踪场景的功能性验证,只需要证明后车的位置始终在EoA之前。由于物理行为和正常行为模型中没有无限执行路径,且场景运行为一次性过程,因此无需对计算时间进行限制。通过PRISM计算属性得到 Pmax=?[Gsafestop]=1 且Pmin=?[Gsafestop]=1 同时计算属性得 Pmax=?[Gunsafestop]=0 且Pmin=?[Gunsafestop]=0 表达式 safestop=po_RTrain≤EoA_RTrain unsafestop=safestop 计算结果表明功能性验证满足,物理行为与正常行为模型正确。图9、图10分别为两车的位置和速度变化曲线,图11为固定闭塞模式下后车EoA的变化曲线,与实际追踪运行情况一致。 图9 两车位置变化曲线 图10 两车速度变化曲线 图11 后车EoA变化曲线 第二步计算危险失效发生的概率,只需对综合行为模型CBM进行定量概率可达性计算。假设场景中考虑的故障包括:ATP计算列车位置错误偏低,时间性瞬态失效概率为RTrainPoerror=7×10-9;ATP与RBC之间安全数据交互错误且被接受,请求性瞬态失效概率为RBCcomError=7×10-9;RBC计算列车EoA错误,时间性永久失效概率为RBCeoaError=7×10-9;ATP请求制动失效,请求性永久失效概率为RTrainBrError=7×10-9。 图12、图13中以RBC计算EoA错误为例,选择了一条失效路径。图12显示了两列车的位置曲线,可见在11个时间单位处,RBC出现故障将错误的EoA值1 000发送给后车,使得后车不断前行,在约38个时间单位、500个位置单位处与前车相撞。图13中同时显示了该失效路径下两车的速度曲线,可见前车制动后在30个时间单位时实现停车,但后车由于接收了EoA错误值,并未及时采取制动措施,而保持在13~14个速度单位之间持续运行。 图12 RBC计算EoA错误使两侧相撞 图13 RBC计算EoA错误使后车未制动 系统隐患是列车位置超过EoA点,即通过PRISM计算场景危险失效概率最大值Pmax=?[true∪unsafestop]=1.607 2×10-12,其中时态逻辑操作符∪的定义为MMDP,πψ1∪ψ2⟺∃i≥0:MMDP,πiψ2∧∀j 本文使用PRISM4.2版本软件,Intel CORE i5处理器,4G内存计算机计算,MDP求解算法选择值迭代算法,功能性验证中生成状态22 168个,概率迁移32 410个,不确定动作选择32 410个,计算时间7.2 s,由于概率行为分布均为1,则概率迁移与不确定动作选择数量相同。危险失效概率计算中,稀疏矩阵占用空间312 M,运行时间257 s,状态空间5 597 187个,概率迁移25 195 039个,不确定动作选择4 152 658个。 本文提出了以Markov决策过程为基础的列控系统行为模型的建模方法,通过该方法可对列控系统中的物理行为、正常行为和失效行为进行建模,并对其中的不确定行为和概率行为进行准确描述,最终经过组合得到综合行为模型CBM。提出了基于CBM模型的定量安全分析方法,克服了经典方法中对离散事件模型危险失效概率计算在完整性和精确性上的不足,运用概率模型检验理论和工具,实现了危险失效概率的计算。以CTCS3级列控系统中的追踪场景为例,证明了本方法的先进性和有效性,证明了该定量安全方法在系统级多实体交互安全分析中的适用性。 参考文献: [1]BSI.EN 50129 C.Railway Applications-Communication,Signalling and Processing Systems-Safety Related Electronic Systems for Signalling[S].United Kingdom:British Standards Institution,2003. [2]JOSHI A,MILLER S P,WHALEN M,et al.A Proposal for Model-based Safety Analysis[C]//Digital Avionics Systems Conference,2005. [3]BOZZANO M,VILLAFIORITA A.The FSAP/NuSMV-SA Safety Analysis Platform[J].International Journal on Software Tools for Technology Transfer,2007,9(1):5-24. [4] BATTEUX M,PROSVIRNOVA T,BRAMERET P A,et al.The Altarica 3.0 Project for Model-based Safety Assessment[C]//Industrial Informatics(INDIN),2013 11th IEEE International Conference on.New York:IEEE Press,2013:741-746. [5]BAIER C,KATOEN J P.Principles of Model Checking[M].Cambridge:MIT Press,2008. [6]HINTON A,KWIATKOWSKA M,NORMAN G,et al.PRISM:A Tool for Automatic Verification of Probabilistic Systems[M].Tools and Algorithms for the Construction and Analysis of Systems,Berlin:Springer Berlin Heidelberg,2006:441-444. [7]FOREJT V,KWIATKOWSKA M,NORMAN G,et al.Automated Verification Techniques for Probabilistic Systems[M].Formal Methods for Eternal Networked Software Systems,Berlin:Springer Berlin Heidelberg,2011:53-113. [8]张曙光.CTCS-3 级列控系统总体技术方案[M].北京:中国铁道出版社,2008.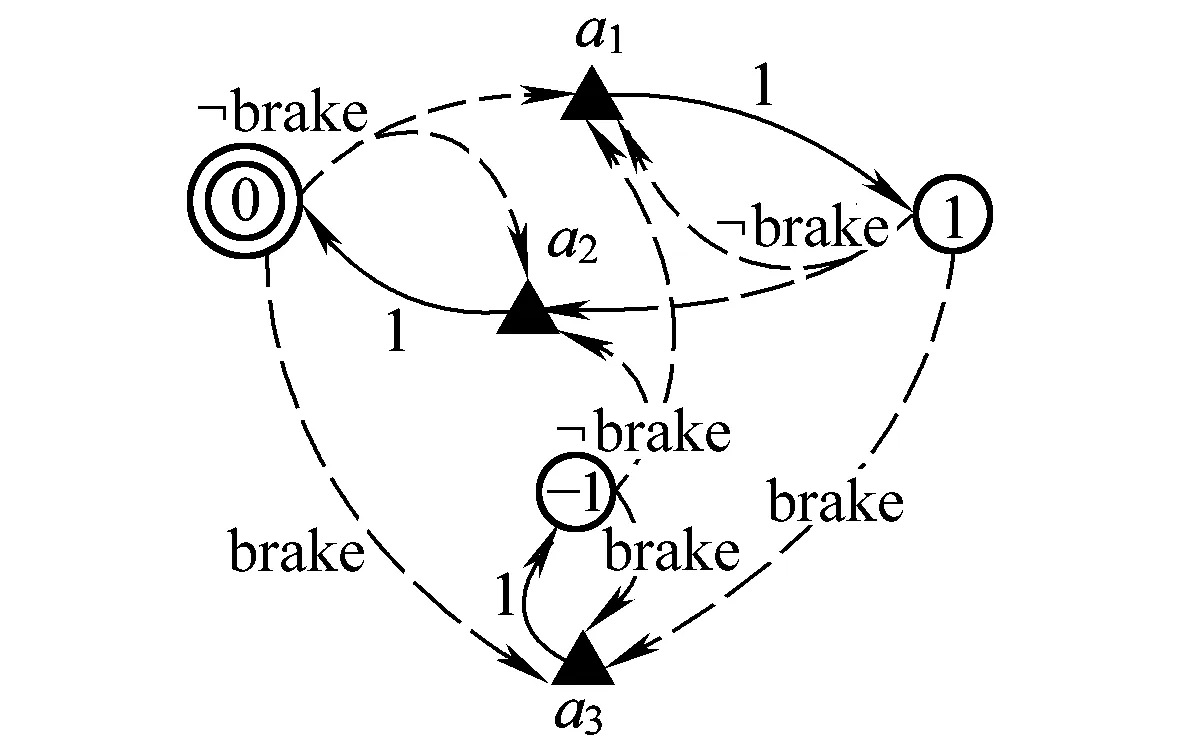
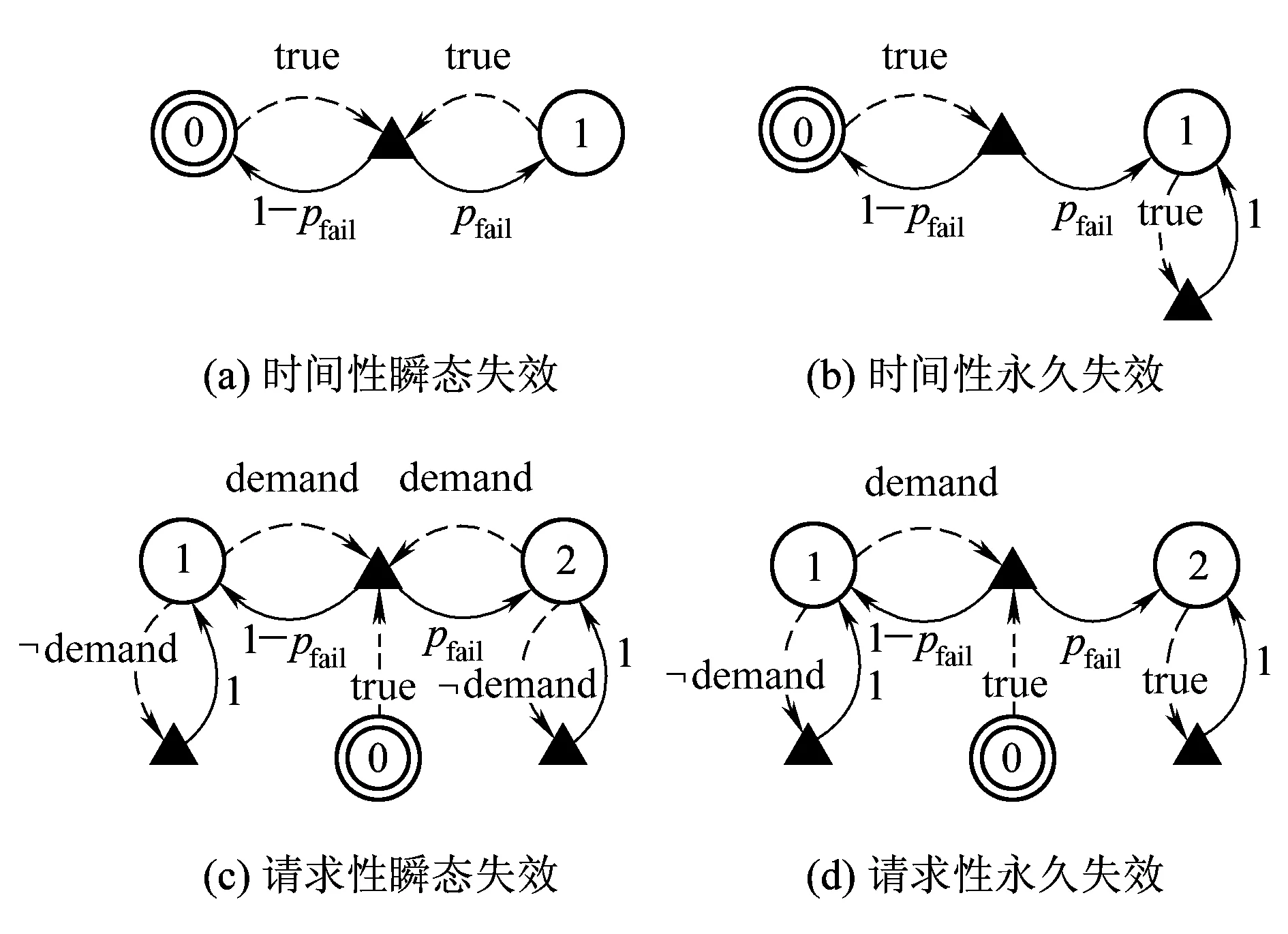
2.3 基于MDP的失效行为建模
2.4 模块化行为模型的综合
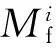
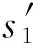
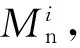
3 基于CBM模型的定量安全分析
3.1 定量安全分析
3.2 基于正常行为模型的验证
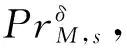
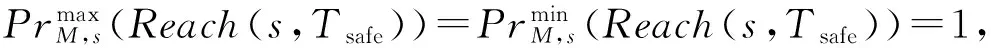
3.3 基于CBM模型的危险失效概率计算
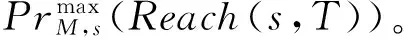
4 列控系统追踪场景的定量安全分析
4.1 追踪场景的CBM建模
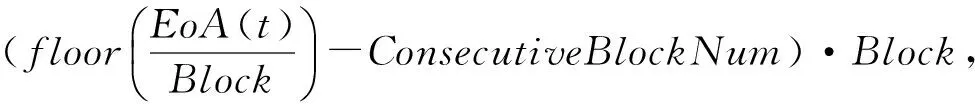


4.2 追踪场景的定量安全分析
5 结论

