对称边界条件下轨道炮有限元/边界元仿真

林志朋，刘振祥，杨　栋，欧阳建明，杨丽佳

(国防科技大学 理学院，长沙　410073)



对称边界条件下轨道炮有限元/边界元仿真

林志朋，刘振祥，杨栋，欧阳建明，杨丽佳

(国防科技大学 理学院，长沙410073)

摘要：基于deal.ii编写了电磁轨道炮有限元仿真程序，建立了拉格朗日运动坐标下电磁轨道炮的有限元仿真模型；通过使用有限元边界元耦合方法可以对电磁轨道炮的边界条件进行计算，而无需对轨道炮周边的空气划分网格，是一种处理电磁场边界问题的有效方法；但是，由于边界元方法，使用的是满秩矩阵，在三维情况下计算量大，利用轨道炮的对称性，使用对称边界条件，减少了参与计算的网格数目，从而减少计算量。

关键词：轨道炮；有限元；边界元；对称边界条件

Citation format:LIN Zhi-peng, LIU Zhen-xiang, YANG Dong, et al.Finite Element/Boundary Element Simulation of 3D Rail Gun with Coupling Method Based on Symmetry Condition[J].Journal of Ordnance Equipment Engineering,2016(3):42-44.

电磁轨道炮通常主要是由两条导轨和一个电枢组成的电磁加速装置。通过组成电磁回路， 形成电磁场，并且与电枢上的电流相互作用，产生洛伦兹力推进其前进。电磁轨道炮的有限元仿真涉及运动﹑电接触﹑热传导等诸多过程，非常复杂。电磁轨道炮在发射过程中会产生速度趋肤效应，影响电枢上电流的分布，从而影响电枢的受力分布以及热分布。对电磁轨道炮的有限元仿真有助于帮助理解电磁轨道炮发射的过程，为改进电磁轨道炮的结构提供指导依据， 降低研究成本。

国内外许多学者对电磁轨道炮的有限元仿真进行了研究，有基于欧拉坐标系的[1]，也有基于拉格朗日坐标系的， 如EMAP3D[2]。采用欧拉坐标系可以采用流线迎风算法来计算迎风项[3]，而本文参考的了EMAP3D的设计原理，采用的是拉格朗日坐标系。在电磁轨道炮仿真中由于角点的存在和对轨道炮的边界条件进行计算的需要，需要额外计算。一种方法是增加额外网格计算周边的环境，一种是使用有限元/边界元耦合方法，国内林庆华等人[4-5]对这两种方法都进行过研究。

本文使用了有限元/边界元耦合的方法，这样可以不需要额外网格，但是由于边界元方法使用了满秩矩阵，在3维情况下计算量大，因此本文利用了轨道炮的对称性，使用对称边界条件，减少了参与计算的网格数目，减少计算量。

1理论模型

电磁轨道由于具有对称性，因此可以通过使用对称边界条件，减少计算量，图1为仿真所用的网格。边界条件的对称约束可以利用矢势和电场在对称面上的反对称性和连续性，结合拉格朗日乘子的方法施加。

图1　仿真所使用的网格

在拉格朗日坐标系下，图1中电枢和导轨采用独立坐标，分别属于运动坐标系和静止坐标系，这样就不需要使用额外网格。两坐标系中电磁场方程是一致的，即：

(1)

运动网格采用固定空间步长的方式运动。通过隐式时间差分的算法计算矢势对时间的导数。

由于在运动边界上电场切向分量需要满足连续性要求[6]，即：

(2)

方括号表示跳变，所以考虑运动后，有：

(3)

其中m代表运动标，s代表静止坐标。上式表明：当使用拉格朗日坐标时，φ值的切向导数在运动边界上是不连续的。可以通过使用离散的φ势或者添加额外的自由度表示这一切向跳变，本文采用后一种方法。为了便于计算交界面上电枢和导轨，采用了不同的自由度，然后通过拉格朗日乘子的方法进行约束，使之保持连续。这样就不用在每一个时间步重复计算有限元矩阵。

由于矢势使用的是拉格朗日元，所以需要添加规范条件，即：

(4)

电枢所受的力可以通过方程：

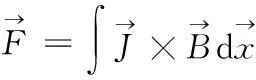
(5)

来计算。之后用计算的力来修正运动时间步长，反复迭代，当两次计算的时间步长接近时，即可认为收敛。

本文程序将电源配置放在python中，因此可以很容易实现对不同波形电流源或电压源的支持。

计算的边界条件可以通过有限元与边界元耦合的方法得到，即除了使用有限元方程，还要加入边界积分方程[7]：

(6)

其中G是格林函数，Ak是矢势的分量，i是结点的编号。

由于电枢运动，在计算每一个时间步时需要重新计算边界元相关的矩阵。为了减少计算量，可以视电枢与轨道中间部分一起运动，这时他们彼此间的相对位置不变，无需重复计算，而只要重新计算导轨首尾的贡献即可。

对称区域的边界元可以通过映射方法得到，由于源点与网格上的场点距离不同，所以仍需要加入计算中。但由于网格只有原来的1/4，所需计算的场点也只有原来的1/4，使计算量大为减少。

2仿真结果

图2为仿真所得的磁场分布图，其中上侧和右下侧为对称面，电枢从左下至右上侧运动。图中可以看到磁场趋于内表面。磁场与右下侧对称面相垂直，结果是对称的。计算量有效减少。

图2　磁场分布图

3结论

三维电磁轨道炮的有限元仿真由于大尺度，多物理，结构复杂，为了进行精确的计算仿真，需要庞大的计算资源以及正确的仿真模型。通过编写代码，掌握了电磁仿真的关键技术，为改进轨道炮的设计提供了理论模型。

本文建立了对称边界条件下，三维电磁轨道炮有限元边界元耦合模型。考虑了拉格朗日坐标系下电场的运动边界条件。通过合理的设计减少了轨道炮系有限元与边界元耦合时所需的计算量。

本文程序仍然有许多可以改进的地方，如本文为了不重复计算有限元矩阵，使用在运动方向上均匀的网格，当轨道炮尺寸比较大时，计算量仍很大,以及由于电枢与轨道的网格不在同一坐标系，需要添加跳变条件。这两点可以通过使用随电枢一起运动的网格改进，在轨道的头端可以通过动态加入新网点保持计算的准确性。由于没有使用逆矩阵减少边界元的计算量，在迭代时计算量比较大。在速度比较低时，时间步长较大，影响对时间的偏导数计算，为了提高精度可以结合非线性的显示差分算法[8]，使用更加细致的网格提高精度，以及通过MPI或GPU对计算进行进一步的加速。

参考文献：

[1]RODGER D,LAI H C.A comparison of formulations for 3D finite element modeling of electromagnetic launchers[J].IEEE Transactions on Magnetics,2001,37(1):135-138.

[2]HSIEH K.A Lagrangian formulation for mechanically,thermally coupled electromagnetic diffusive processes with moving conductors[J].Magnetics,IEEE Transactions on,1995,31(1):604-609.

[3]XU E X,SIMKIN J,TAYLOR S C.Streamline upwinding in a 3-D edge-element method modeling eddy currents in moving conductors[J].IEEE transactions on magnetics,2006,42(4):667-670.

[4]林庆华,栗保明.电磁轨道炮三维瞬态涡流场的有限元建模与仿真[J].兵工学报,2009(9):1159-1163.

[5]林庆华,栗保明.有限元/边界元耦合法计算电磁轨道炮三维瞬态涡流场[J].南京理工大学学报(自然科学版),2010(2):217-221.

[6]SATAPATHY S,HSIEH K.Jump conditions for Maxwell equations and their consequences[J].AIP Advances,2013,3(1):12120.

[7]MEUNIER G E R.The finite element method for electromagnetic modeling[M].John Wiley & Sons,2010.

[8]HANNALLA A,MACDONALD D.Numerical analysis of transient field problems in electrical machines[A].1976:893-898.

[9]李小将，杨成伟，武昊然. 基于单参数灵敏度方法的轨道炮系统性能影响因素分析[J].兵工自动化，2014(9):4-6.

(责任编辑周江川)

Finite Element/Boundary Element Simulation of 3D Rail Gun with Coupling Method Based on Symmetry Condition

LIN Zhi-peng, LIU Zhen-xiang, YANG Dong, OUYANG Jian-ming, YANG Li-jia

(College of Science, National University of Defense Technology, Changsha 410073, China)

Abstract:This article created finite element program and model for rail launch based on deal.ii in Lagrange coordinate frame. By using coupling finite element/boundary element coupling method, we can calculate boundary condition without air grid surround rail gun. It is a valid method to handle boundary problems of electromagnetic without the perimeter of the rail gun air mesh. But for boundary element method using full matrix which will cost a lot of calculation in 3D situation, we would better using symmetry conditions for rail gun to reduce the grid number and calculation.

Key words:rail gun; finite element; boundary element; symmetry condition

文章编号：1006-0707(2016)03-0042-03

中图分类号：TM303.1

文献标识码：A

doi:10.11809/scbgxb2016.03.011

作者简介：林志朋(1988—)，男，硕士研究生， 主要从事电磁发射与等离子体研究。

基金项目：国防预研项目

收稿日期：2015-10-09；修回日期：2015-10-22

本文引用格式：林志朋，刘振祥，杨栋，等.对称边界条件下轨道炮有限元/边界元仿真[J].兵器装备工程学报，2016(3):42-44.

【装备理论与装备技术】