鞍式支承钢平管桥模型试验、有限元分析与简化计算方法

沈晔

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

鞍式支承钢平管桥模型试验、有限元分析与简化计算方法

沈晔

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

基于3组钢平管桥负弯矩试验结果进一步比对规范计算的合理性，同时验证非线性有限元模拟的准确性，对20个自承式平直型钢管桥模型展开参数分析。研究支承角度、管壁厚度、支承长度、钢管直径等参数对支座处钢管环向应力的影响。并将计算结果与现行管桥设计规程推荐的计算方法进行对比。研究结果表明：自承式管桥的支承断面为结构设计的控制性断面，按现行设计规程设计大直径管桥时，有较大的安全储备。最后，基于参数分析，回归给出最大环向弯矩计算公式，与有限元结果吻合良好。

钢平管桥；鞍式支承；有限元；环向弯矩

0 引言

自承式钢管桥是输送介质的管道工程穿越河流等障碍物的主要结构形式之一，具有施工方便，便于维护等优点。自承式钢管桥的支座形式有鞍式支座和环式支座等。其中：鞍式支座因其结构简单、施工方便的特点得到了广泛的应用。

自承式钢平管桥主要根据《自承式给水钢管跨越结构设计规程》(CECS 214：2006)中规定的进行内力计算和构造设计，其支承处管壁环向弯矩是钢平管桥的设计控制弯矩，根据《规程》第6.1.3条的公式进行计算。在实际工程应用中，普遍觉得由该公式计算所得的环向弯矩比以往的经验偏大，依据该结果在工程设计中不得不选用较大的钢管壁厚而不尽合理。

本文结合3组钢平管桥的支承负弯矩模型试验，通过试验结果进一步比对《规范》的计算值，并在试验结果的基础上，确立合理的有限元验证模型与参数，对20组不同跨度、管径、壁厚与支承角度的钢平管桥的有限元分析计算，研究管桥的内力分布规律，为管道结构设计计算提供更合理的参考。

1 模型试验

1.1 试验概况

该项试验研究以管桥支座处弯矩分布为主要试验研究对象，设计了3个1/2模型试件。试件具体参数如表1所列，钢管选用DN 500钢管，壁厚6 mm，钢管长度为8 800 mm，支墩采用C 30混凝土内配构造钢筋，钢平管及钢支座均采用Q 235钢。

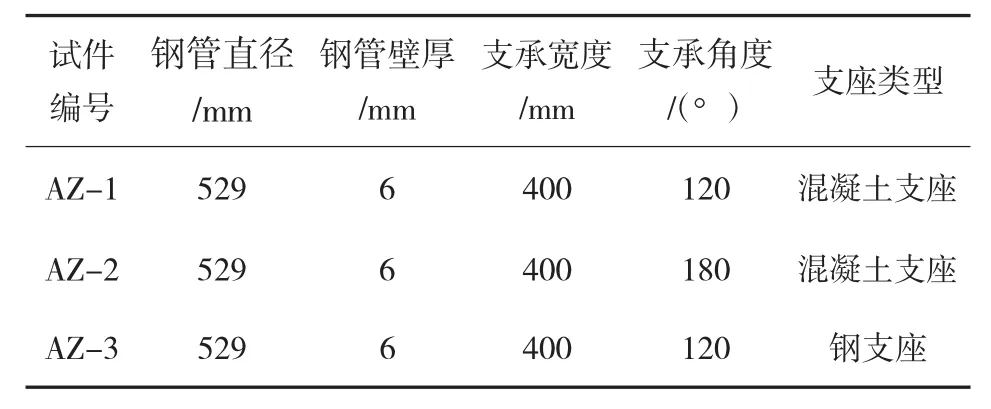
表1 试件参数表

1.2 加载方案

试件采用简支支座，一端悬臂加载，如图1所示，跨中通过油压千斤顶以限制钢平管竖向位移。悬臂端通过100 t的油压千斤顶单点施加集中力，为防止内支座B内侧钢管先于外侧破坏，经计算，跨中加载点位置如图1所示，在加载时，跨中千斤顶先施加微小的力以保证其竖向位移，悬臂端预加载后，连续加载直至试件破坏。

1.3 管桥破坏模式

3个试件的试验均显示，鞍式支座钢平管桥破坏均发生在支座处。试件在弹性阶段时，随着悬臂端荷载增加，钢管环向变形明显。在支座两侧面，由于支座对钢管环向变形约束作用，两侧钢管沿支座方向呈不同的凹曲状态；在弹塑性阶段时，钢管支座上部环向变形加快，与支座接触范围出现明显凹曲，底部钢管由于较大支座负弯矩及支座多向约束作用在离支座约50 mm处鼓曲，承载力达到极限。

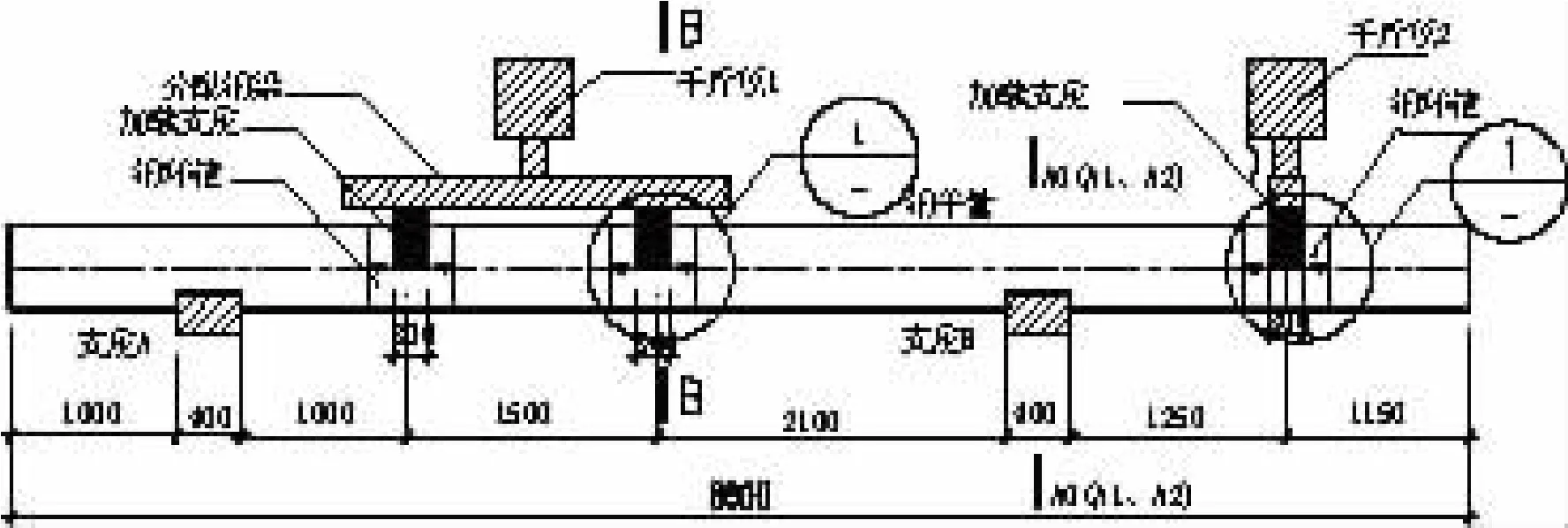
图1 加载示意图

3个试件中，较混凝土支座，钢支座的钢管凹曲范围较大，屈曲程度最为严重，角部应力集中最明显；对于支承角度为180°的试件，对环向变形约束效果最好，凹曲程度最轻，承载力最高。

1.4 环向弯矩比较

环向弯矩是该试件试验重点关注的力学性能，是支座及钢管设计的重要指标。图2为鞍式支座示意图。

图2 鞍式支座示意图

在图2中，截面上的A、B及C点为截面主要控制部位，其中，C点应力集中受力复杂，为危险部位。

在C点屈曲变形前，截面环向应变增长迅速，且为主控应变。根据试验测试结果，将关键点在屈服荷载下环向弯矩计算结果列入表2。

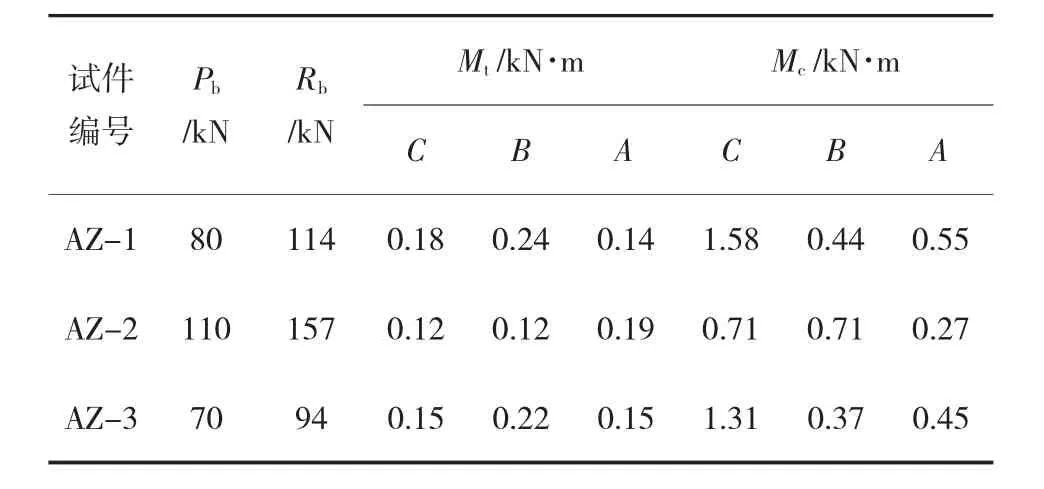
表2 试件参数表

在表2中，Pb为屈曲荷载，即钢管局部变形时对应的荷载；Rb为支座反力；Mt为环向弯矩试验值；Mc为同等工况下环向弯矩计算值，根据《自承式给水钢管跨越结构设计规程》计算所得。

由表2分析可知，环向弯矩试验值远小于环向弯矩规范设计值，即相同的支座反力下，对于试件AZ-1、AZ-2及AZ-3的C点处环向弯矩，试验值分别为设计值的11%、17%及12%，B点和A点试验值较设计值也偏小，可见规范设计值偏于安全，提供的计算方法得到的结果过于保守。

2 有限元模型的建立

以上述三个模型试验为基础，确立符合试验结果的ABAQUS有限元模型和参数，并采用该有限元参数建立多组管桥实例进行分析计算，最终归纳出能指导工程应用的建议和公式。

2.1 边界条件

构件的受力模式与试验加载方案相同，均为跨中限制竖向位移，悬臂加载模式。支座截面与钢管截面之间属于边界高度分线性接触问题，拟将其设置成切向为罚函数摩擦模型，即使用摩擦系数来表示接触之间的摩擦特性。钢管与支座接触设置法向硬接触，允许只传递的接触压力，切向为摩擦接触。

2.2 单元选取

建模中钢管均采用4节点减缩积分 (S4R)单元，S4R单元为线性、有限薄膜应变、缩减积分的四边形壳单元。其他构件均采用solid65实体单元建模。

2.3 材料选取

钢材采用等向弹塑性模型 (Plasticity)，满足Von Mises屈服准则。钢材本构选用强化模型，钢材的弹性模量E及泊松比ν分别取195 000 N/mm2及0.3。该项研究进行了钢材标准拉伸试验，有限元模拟与试验对照时材性取实测值。Abaqus中对混凝土有多种本构模型，为了更好模拟试验，选用混凝土损伤模型，此模型基于塑性并带有连续损伤模型，假定混凝土拉伸开裂破坏及压缩破坏。

2.4 初始几何缺陷施加

在实际工程中，钢管在没有承受荷载之前加工、运输等原因会不可避免的存在初始几何缺陷，导致试件平面外变形从加载开始时以初始缺陷的形态展开且不断增加，使其承载力降低，因此在ABAQUS模拟时需要考虑初时几何缺陷的影响。施加初始几何缺陷时采用了一致缺陷模态法。

2.5 有限元模拟与试验对比

分别对3个试件进行模拟分析，对钢管加入整体初始缺陷，进行屈曲分析。图3为钢管屈曲破坏模式对比云图，可以看出ABAQUS模拟的屈曲破坏基本与试验破坏模式吻合，该项研究所建立的有限元模型能够较为准确地模拟钢管的破坏模式。

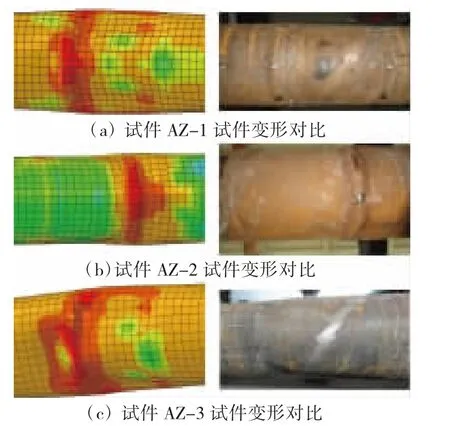
图3钢管屈曲破坏模式对比云图

图4 为钢管的P-Δ曲线对比图，表3为试验与有限元计算承载力对比表。

试件AZ-1：有限元计算与试验结果吻合良好，计算刚度与试验刚度基本一致，计算极限承载力与试验值相差1.6%，屈服承载力与试验值相差6%。

试件AZ-2：有限元计算与试验结果基本吻合，计算刚度略大于试验刚度，计算极限承载力与试验值相差0.23%，屈服承载力与试验值相差11%。

试件AZ-3：有限元计算与试验结果吻合良好，计算刚度与试验刚度基本一致；计算极限承载力与试验值相差0.85%，屈服承载力与试验值相差14%；下降段吻合良好。

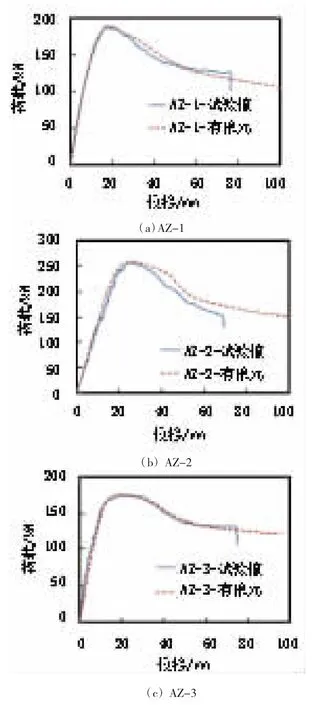
图4 P-Δ关系曲线对比图

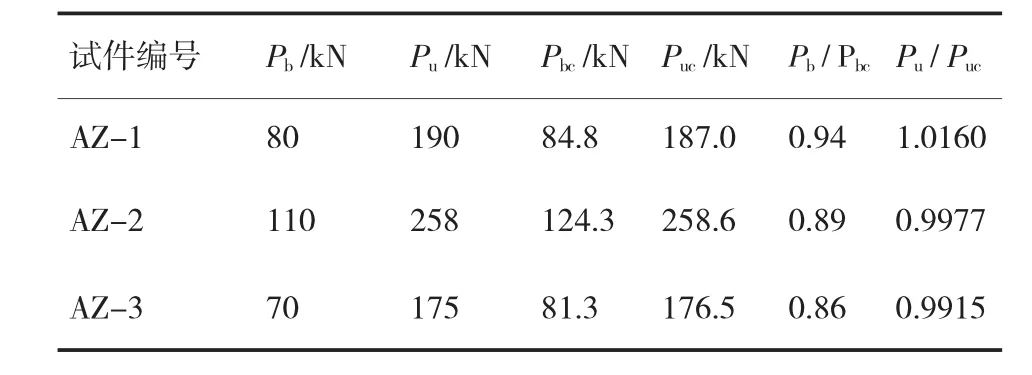
表3 试验与有限元计算承载力对比表

通过图4钢管屈曲模式对比图与表3试验与有限元计算承载力对比表可见有限元计算的P-Δ曲线和试验结果符合很好，该项研究所建立的有限元模型能够较为准确地模拟钢管的P-Δ曲线。

3 管桥有限元模拟

前文利用ABAQUS有限元程序建立了钢平管桥的有限元模型，并用该项研究的试验数据验证了模型的合理性。在此基础上，本节将对鞍式支承钢平管桥在实际工况荷载作用下的力学性能进行分析，拟给出支座处钢平管桥环向弯矩的设计建议。

3.1 管桥参数选取

有限元分析模型选择工程中常用的鞍式支承钢平管桥结构，分析不同管径、壁厚、跨度、支座宽带及支承角对钢管环向应力的影响。模型中荷载取钢管自重和满载水时荷载之和，支座类型为混凝土支座。试验模型的详细参数如表4所列。

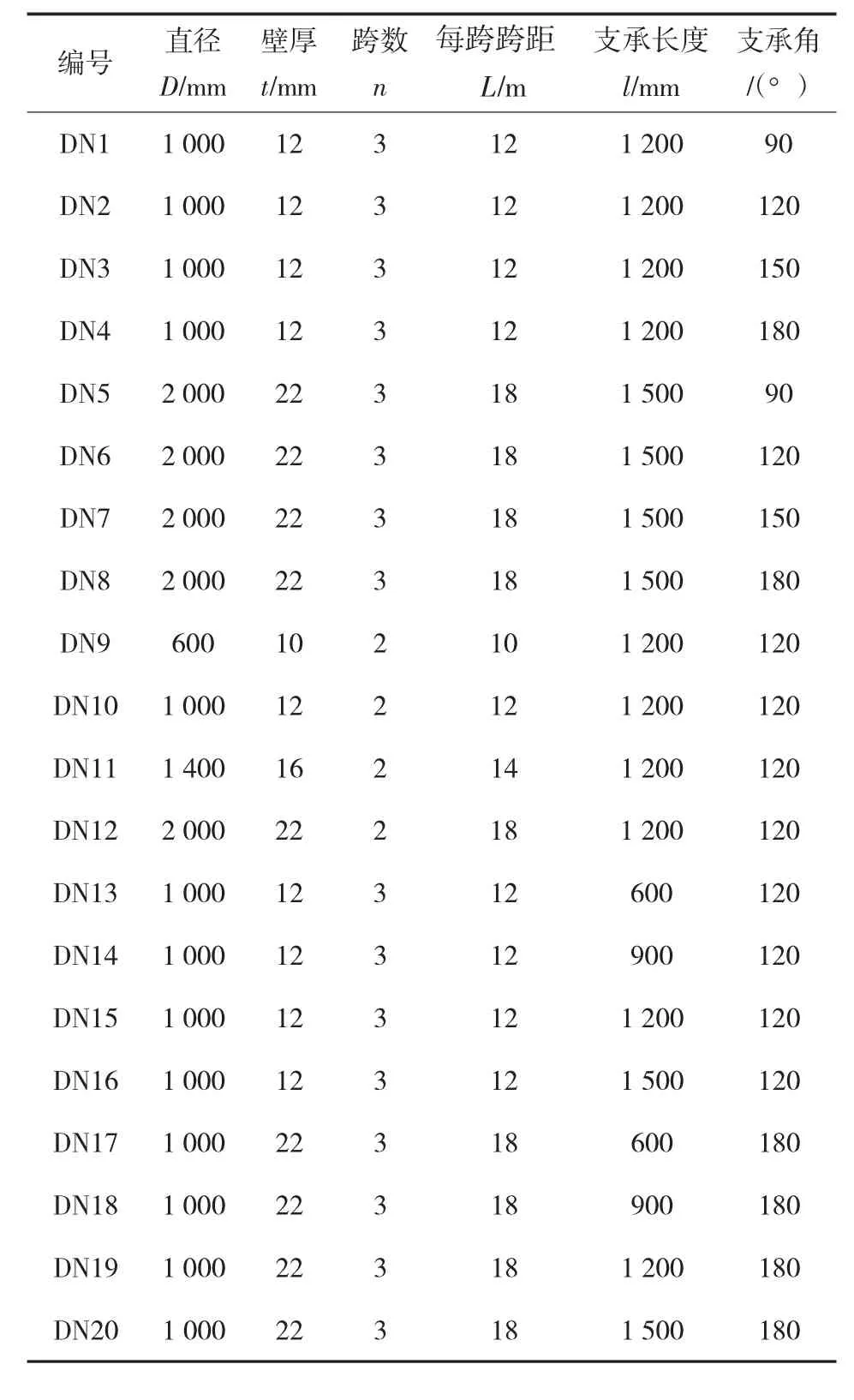
表4 鞍式支承钢平管桥模型参数表

需要说明，有限元分析模型中未考虑支座上部钢套箍和钢管与鞍式支座之间薄橡胶垫的影响。

3.2 主要结果与分析

3.2.1 支撑角度的影响

鞍式支承钢平管桥模型环向应力分析有限元及规范计算结果对比见表5、表6所列，表中A、B及C表示钢管截面不同的位置，具体见图2所示。图5为支座控制截面C点环向弯矩Mθ与Rr关系曲线图。

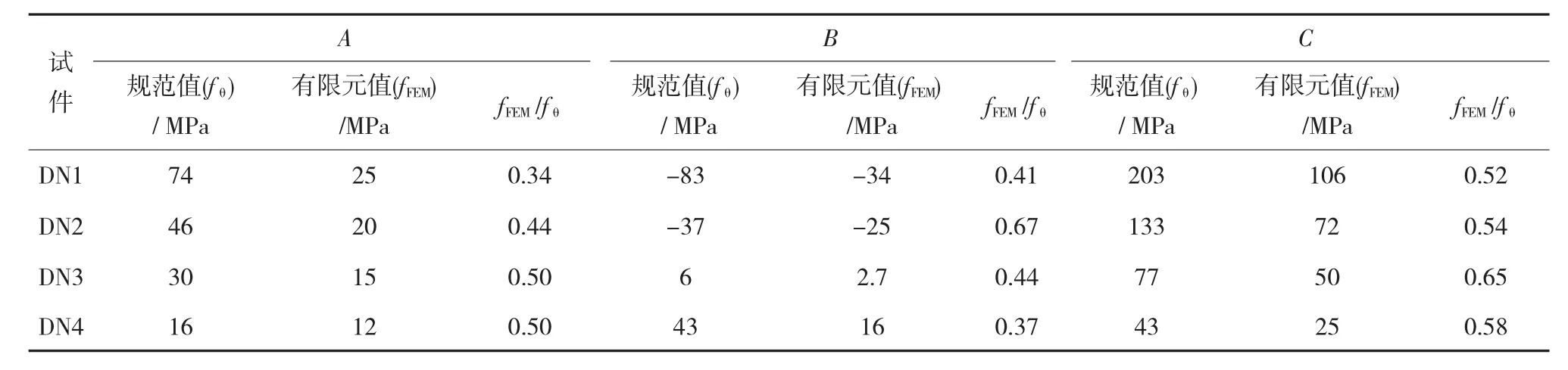
表5 管径1 000 mm变角度环向应力结果对比表

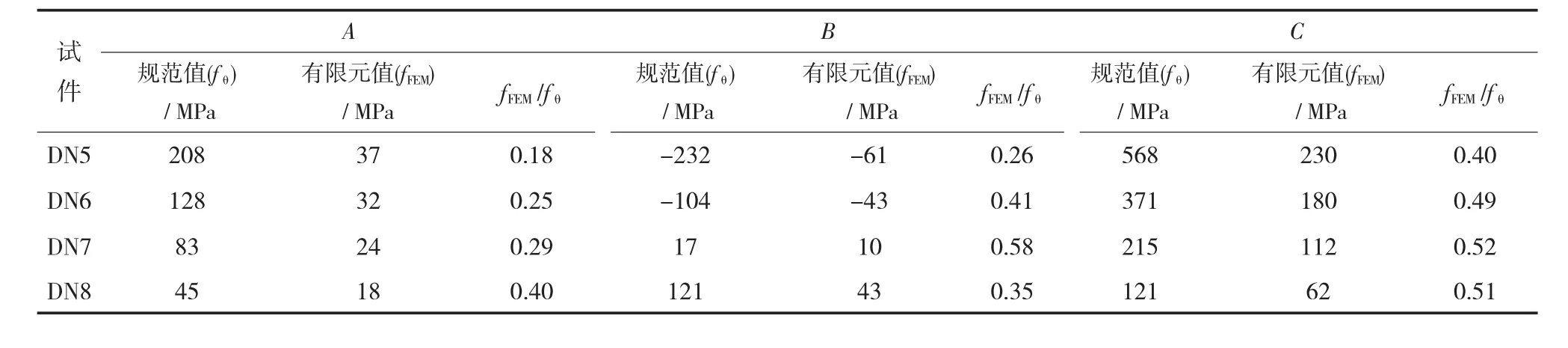
表6 管径2 000 mm变角度环向应力结果对比表

（1）DN1～DN8管桥支承截面A、B、C三点处有限元计算的钢管最大环向应力均小于规范计算结果，控制截面C的有限元计算弯矩为规范计算值的40%～65%。

（2）随着支座支承角度的增加支座环向应力大幅减小。

3.2.2 管径的影响

鞍式支承钢平管桥模型环向应力分析有限元及规范计算结果对比见表7所列。

（1）试件DN9～DN12管桥支承截面A、B、C三点处有限元计算的钢管最大环向应力均小于规范计算结果，控制截面C的有限元计算弯矩为规范计算值的35%～66%。

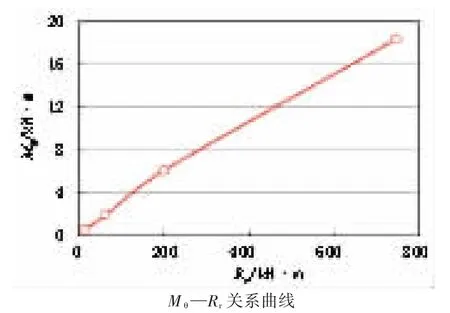
图5 C点环向弯矩与Rr关系曲线图

（2）随着管径的变大，支承截面A、B、C三点处有限元计算的钢管最大环向应力与规范计算结果的比值变小，A点从53%变化到20%，B点从75%变化到41%，C点从66%变化到35%。说明随着管径的增加，规范计算值与有限元计算值的差别增大。

（3）试件支承截面A、B、C三点之间的应力比例关系与规范计算结果相近。

（4）如图5所示，说明当支承角度一定时，环向弯矩Mθ与Rr呈近似线性关系。

3.2.3 支承长度影响

鞍式支承钢平管桥模型环向应力分析有限元及规范计算结果对比见表8所列，表8为支承角度为120°及180°时支承长度从600 mm～1 500 mm的关键点的环向应力对比情况。图6为C点环向应力及环向弯矩与支承长度关系曲线图。具体分析如下：

（1）DN13～DN20管桥支承截面A、B、C三点处有限元计算的钢管最大环向应力均小于规范计算结果，控制截面C的有限元计算弯矩为规范计算值的53%～59%。

（2）随着支承长度的增加最大环向应力（C点处环向应力）近似幂函数逐渐减小，如图6(a)所示，适当增大支承长度有利于减小截面环向应力；随着支承角度增大最大环向弯矩近似不变，最大环向弯矩与支承长度近似直线关系，如图6(b)所示。说明合适支承宽度下，支承宽度对环向弯矩大小影响不大。

表7 变管径环向应力结果对比表

表8 变支承长度环向应力对比表

4 环向弯矩计算公式

基于试验研究及有限元参数分析，支承处局部应力规范计算偏于保守，研究发现支承处钢管环向最大弯矩与支承反力及钢管内半径之积成正比，影响环向弯矩因素繁多，其中支承角度及钢管的厚径比是影响计算结果的重要因素，为了优化设计，经有限元参数分析及利用最小二乘法对数据进行多重拟合，基于弹性设计方法，给出支承管壁处环向最大弯矩计算公式（1）：

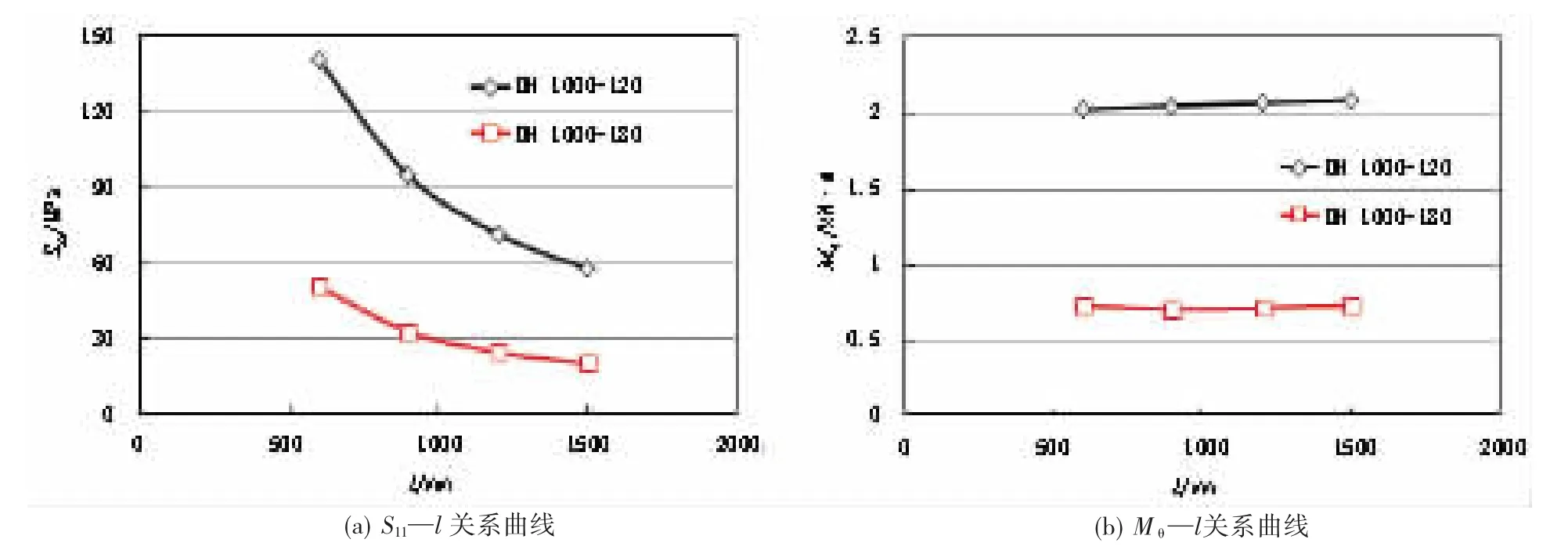
图6 C点环向应力及环向弯矩与支承长度关系曲线图

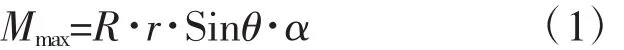
式中：Mmax为作用于鞍式支撑长度上管壁的最大环向弯矩，N·mm；R为支座竖向反力，N；r为钢管内半径，mm；θ为支承角度，90°～180°；α为考虑管径、管厚、跨度及支承长度等综合影响系数，建议取0.011。

由环向弯矩计算得出环向应力结果及比对如表9所列。计算分析表明，该公式和有限元计算结果吻合较好，规范计算结果过于保守，建议优化规范计算公式。

5 结论

通过3组钢平管桥试验验证有限元分析的准确性，并在此基础上进行多参数非线性有限元分析，小结如下：

（1）考虑初始缺陷的非线性有限元分析结果与试验结果吻合良好，环向屈服承载力最大误差在16%以内，极限承载力在2%以内。

（2）在试验及有限元建模基础上进行多参数管桥有限元分析，有限元计算结果是规范计算结果的40%左右，随着支承角度的变化，支承截面A、B、C三点处的应力变化规律与规范计算相同。在有限元基础上，考虑多参数影响下给出支座截面处钢管最大环向弯矩的计算建议。

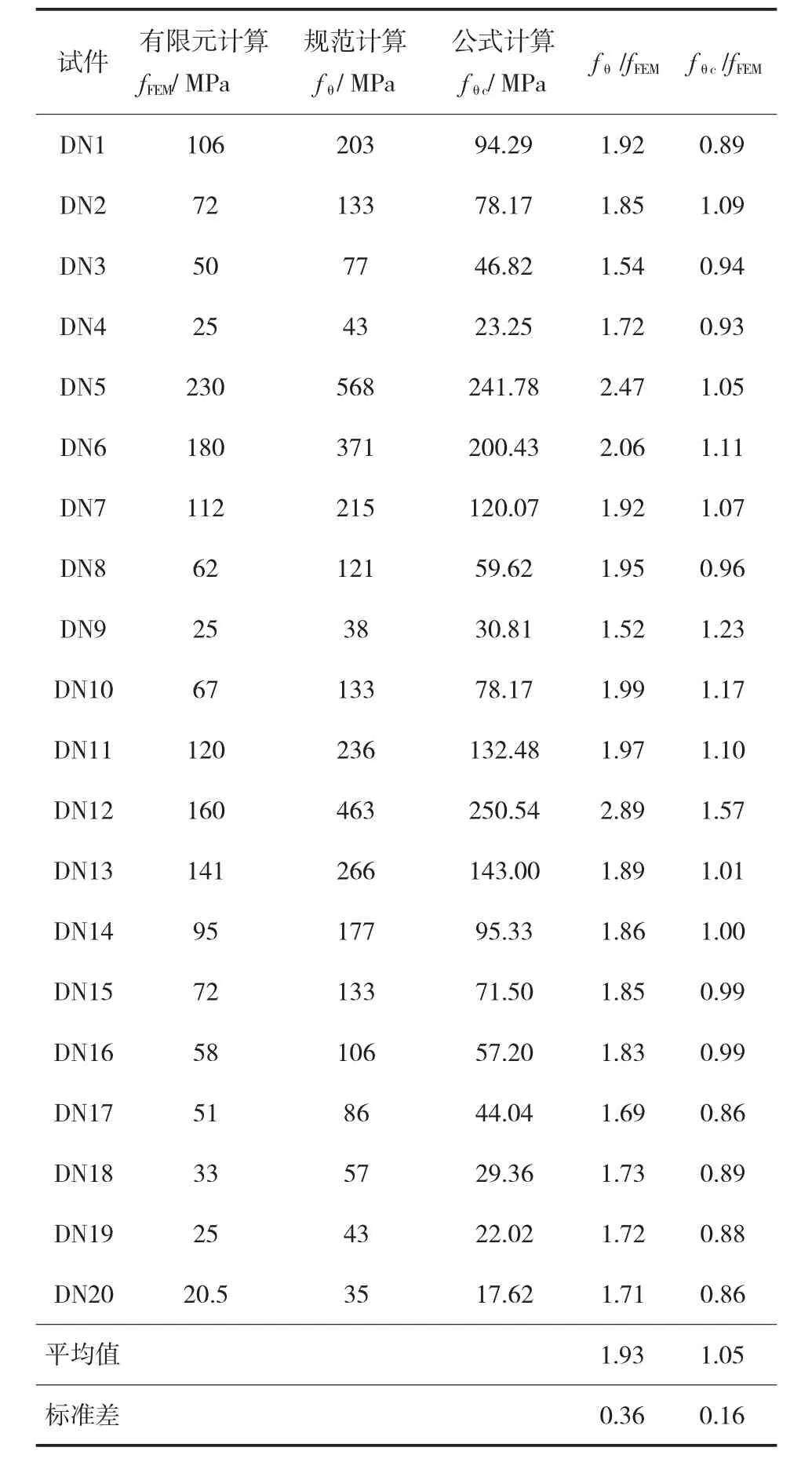
表9 由环向弯矩计算得出的环向应力计算结果对比表

U441+.5

A

1009-7716（2016）05-0084-06

10.16799/j.cnki.csdqyfh.2016.05.023

2016-02-19

沈晔（1972-），男，浙江宁波人，高级工程师，第二设计研究院副总工程师，从事市政工程结构设计审核工作。