大尺寸CFRP约束混凝土方柱的轴心抗压试验研究*

单　波, 蔡　静,肖　岩, Giorgio Monti,2

(1.湖南大学 土木工程学院，湖南 长沙　410082；2.罗马第一大学，意大利 罗马　00917)



大尺寸CFRP约束混凝土方柱的轴心抗压试验研究*

单波1†, 蔡静1,肖岩1, Giorgio Monti1,2

(1.湖南大学 土木工程学院，湖南 长沙410082；2.罗马第一大学，意大利 罗马00917)

摘要：试件的尺寸对于碳纤维增强塑料(CFRP)约束混凝土柱的性能具有重要影响，但目前在CFRP约束混凝土尺寸效应方面的研究基本上还处于空白.基于对7种不同倒角半径的大尺寸CFRP约束混凝土方柱的轴心抗压试验，获取了各组试件的破坏模式、抗压强度、应力-应变曲线、外包CFRP应变分布等基本力学性能，并与已有小尺寸试件的试验结果进行比较和分析.研究结果表明,试件的抗压强度随倒角半径比的增大而增大，外包CFRP对直角试件几乎无增强作用；所有试件的破坏都是由外包CFRP的拉断所导致，断裂位置均位于倒角范围内，应力集中的现象明显；约束效应比MCR可以较好地反映尺寸效应对抗压强度影响，试件尺寸的增大显著降低CFRP的约束效应；外包CFRP的极限应变低于其材性试验结果35%以上，明显大于对应的小试件试验结果；已有模型的计算结果与本试验的实测结果存在显著差异，故有必要考虑尺寸效应的影响.

关键词：FRP；约束混凝土；方柱；轴心受压；尺寸效应

纤维增强塑料 (FRP)具有重量轻、强度高、耐腐蚀性好和施工简便等特性，在土木工程领域，特别是混凝土结构加固及改造方面得到广泛应用.采用FRP外包混凝土柱，可以形成约束混凝土结构，当混凝土柱轴向受压时产生其侧向膨胀，约束材料FRP受拉对核心区混凝土产生约束应力，使其处于三向受压状态，从而显著提高混凝土柱的变形能力和承载能力[1].

目前，国内外对于FRP约束混凝土开展了大量研究，取得了不少的研究成果，部分学者还提出了约束本构模型及设计方法[2].但总的看来，现有研究主要集中在FRP约束混凝土圆柱方面，而在实际结构中，方形或矩形柱更为普遍.因此，对FRP约束方形及矩形截面柱进行研究很有必要，但这个问题更为复杂，因为FRP约束作用于方形及矩形截面柱所产生的围压是非均匀的，约束效应的影响因素更多[3].

在国际上，Mirmiran等[4]是最早对FRP约束矩形截面柱进行试验研究的研究者之一，其研究表明，倒角半径是影响FRP约束效应的一个主要因素，倒角半径过小，约束效应难以体现.Lam等[5-6]对小尺寸外包FRP矩形(方形)柱进行了试验，研究表明，FRP约束能有效提高混凝柱的抗压强度和延性，并在分析了既有试验数据后提出相应的本构模型和强度模型.Wang和Wu[7]对72个混凝土小尺寸试件进行轴压试验，得出试件的抗压强度与倒角半径比2r/b近似呈线性关系，也提出了相应的本构模型和强度模型.吴刚等[8-9]在既有试验数据的基础上，给出判断FRP约束方柱强、弱约束的界限值，提出二次抛物线加直线的应力-应变模型.国内其他学者在此领域也开展了相关的研究工作[8-12].

目前，关于FRP约束方形(或矩形)柱的试验绝大部分以小试件为主[4-7,13]，试件边长不超过250 mm，高度不超过600 mm，与实际结构柱尺寸相距甚远.Pessiki等[14]的研究表明，此类小试件的试验研究结果相比于实际加固柱，存在较大误差.Rocca[15]测试了截面尺寸分别为324 mm，457 mm，648 mm和914 mm的方形试件，实验结果表明，小试件和大试件在轴向力作用下的应力-应变曲线有很大不同.Wang等[16]测试了大尺寸FRP约束钢筋混凝土方柱，结果显示CFRP约束增加了混凝土柱的变形性能，但其承载能力的提高相对有限.从已有研究成果来看，试件的尺寸对FRP约束混凝土方形柱有显著影响，但这方面的试验开展得很少，也不系统.本文针对这一研究的盲区，设计了一系列不同倒角半径的大尺寸CFRP约束混凝土方柱，进行轴心抗压试验研究，以期填补研究空白，为后续的CFRP加固方柱设计提供参考.

1试验设计

1.1试件设计和材料特性

文献[7]中进行了CFRP约束混凝土方柱的试验，标准方形试件截面尺寸为150 mm×150 mm，高度为300 mm，倒角半径依次变化6次，混凝土设计强度等级为C30和C50.本文参考了该试验，使本试验的研究成果能够较为准确地反映试件尺寸的影响.本试验按照不同的倒角半径r依据相似比例尺设计了7组CFRP加固大尺寸试件，标准试件的截面尺寸为300 mm×300 mm，高度为600 mm，每组均有3个试件.倒角半径r依次变化：0，15，30，60，90，120和150 mm，其中，r=0和r=150 mm分别代表方柱和圆柱.每组加固试件都制作了一组与之对应的素混凝土试件.一共制作了14组试件，共计42个.需要说明的是，虽然本试验设计的试件与实际结构柱仍然有较大的尺寸差异，但与文献[7]以及大量其他研究者所进行的FRP约束试件相比较，在尺寸上显著增大，因此，本文称之为“大尺寸试件”是合适的.混凝土设计强度等级为C30，具体配比为：水泥∶砂∶石∶水=1∶1.90∶3.10∶0.56，标准养护28 d,立方体抗压强度为33.6 MPa.试验用的单向碳纤维布为南京生产，型号为HITEX-C300，名义厚度为0.167 mm.配套环氧树脂为长沙生产的碳纤维加固专用浸渍树脂.按照GB/T 3354-1999《定向纤维增强塑料拉伸性能试验方法》制作了CFRP小试件.单向抗拉试验结果如表1所示.

表1　CFRP材性试验结果

1.2试件制作

试件采用定制的钢模浇筑，每种规格的钢模3个，一共21个试模.浇筑时，混凝土分3层浇捣，每层混凝土约为试件高度的1/3，采用插入式振捣器分层振捣，振动至混凝土表面不出现明显的气泡.试件分两批浇筑，一批为对比试件，另一批为加固试件.试件完成浇筑后，在室温下放置48 h，拆模后在室内放置30 d，再进行外包CFRP.

加固前，先清除试件表面杂物，在干燥状态下涂刷底胶，然后再分层外包碳纤维布，每层搭接长度为100 mm，在包裹下一层碳纤维布前，用专用的刮子沿纤维方向反复挤压，以排除气泡并使树脂更好地浸润碳纤维丝.所有加固试件均外包3层CFRP.试件完成加固后，在室内放置14 d，然后进行抗压试验.

1.3试验装置和加载制度

本试验进行单轴抗压试验，现有试验表明，FRP增强层的应变分布不均匀，在角部附近会产生较为显著的应力集中.因此，本试验在试件的中间截面处粘贴一定数量的应变片，具体位置为：对于方柱(r=0)，横向应变片粘贴在角部的最边缘和每条边的中点(b/2处)，共12个，纵向应变片粘贴在b/2处，共4个；对于圆柱(r=150 mm)，横向和纵向应变片均粘贴在圆周的4等分点处，共8个；对于其他截面形式，横向应变片粘贴在倒角的中点、倒角的起始部位(切线处)和每条边的中点(b/2处)，共16个，纵向粘贴在b/2处，共4个.每种截面应变片的粘贴情况如图1所示，图中，M表示边长中点处(b/2处)，C表示倒角中点处，T表示倒角的起始部位(切点处).

加载设备为1 000 t电液伺服控制的压力试验机，试验时，在试件中部位置安装轴向变形测试架，试验架卡在试件上，并对称安装两个高精度的位移计，位移计可以沿导轨在轴向自由滑动，如图2所示.荷载由压力机内置传感器测量，所有数据均采用DH3821数据采集系统同步采集和记录.

图1　CFRP表面应变片分布示意图

测试时，先对试件进行预压，预压荷载不超过预估极限荷载的30%，通过4个轴向应变片检查试件的对中情况，如最大应变读数与最小应变读数不超过10%，即认为试件处于理想的轴心受压状态，随即卸载，并开始正式加载.在试验的开始阶段，采用力控制加载模式，加载速度为3 kN/s.当加载至预估极限承载力的90%时，采用位移控制加载，加载速度为0.01 mm/min，直至试件破坏.

图2　测量设备布置图

2试验结果与分析

2.1破坏现象及破坏模式

7组CFRP约束混凝土方柱试件的破坏部位均位于试件中部约30～40 cm高度，最终破坏模式都是外包CFRP增强层被拉断，并且试件发生破坏前会连续发出“噼啪”的声音，最终在破坏位置3层CFRP增强层突然断裂，并伴随着很大的声响，核心区混凝土压溃飞溅.破坏的突然性及破坏程度随着倒角半径的增大而增大.

图3　CFRP约束混凝土柱破坏模式

对于小倒角半径试件(r≤30 mm)，CFRP增强层的断裂口基本上集中在一处，破坏位置均在倒角圆弧的中点处附近，断口比较整齐，如图3(a)-图3(c)所示.当倒角半径较大时(r≥60 mm)，CFRP增强层的断裂位置出现一定的离散性，拉断部位主要发生在倒角中心附近或倒角起始部位，或这两个部位均出现断裂现象，且试件不止一处发生破坏，断口纤维布呈多条状，如图3(d)-图3(g)所示.试验中，检查所有试件的外包CFRP，均没有观察到明显的剥离和搭接破坏现象，因此，可认为对于此类试件，CFRP取100 mm搭接长度是合理可靠的.

对比文献[7]中的试验，如前所述，其试件边长为150 mm，高度为300 mm，CFRP的搭接长度为150 mm.试验中r较大的试件，CFRP出现了搭接破坏，或为剥离与拉断的混合破坏.这表明，CFRP约束混凝土所需的搭接长度与试件的尺寸大小不存在必然的相关性.此外，在该试验中，当r较大时， CFRP的断裂位置出现在倒角范围以外的侧面(即CFRP的平直段)，与本试验有一定差异.

2.2应力-应变曲线

表2给出了各组试件强度的测试结果，表中fco′为每组无约束混凝土柱的抗压强度平均值，fcc′为每组约束混凝土柱的抗压强度.由表2可知，随着倒角半径r的增加，试件的抗压强度不断提高.图4给出了各组试件典型的应力-应变曲线，包含了未加固试件.图4中，纵轴为应力，横轴为CFRP的横向应变和试件的轴向应变.其中，横向应变为CFRP中部4个应变片的平均值(M1-M4)；对于纵向应变，由于两个位移计在加载的起始阶段读数变化不大，因此，在轴线应变达到6 000 με之前，采用CFRP上4个纵向应变片读数的平均值，此后采用2个位移计读数的平均值.试验表明，在6 000 με这个读数点上，两者的差别较小，在3%～8%之间.由图4可以看出，在加载初期，CFRP约束混凝土方柱应力-应变曲线与素混凝土的曲线基本一致.当试件的压应力超过素混凝土的峰值应力后，曲线出现一个明显的转折点，转折点后的应力-应变行为与倒角半径r密切相关，且曲线在达到素混凝土峰值应力后的斜率随着倒角半径的增加而增大.为了便于比较和分析，定义倒角半径比为rc，按下式计算：

rc=r(b/2)．

(1)

按照公式(1)，rc=0为方柱，rc=1为圆柱.

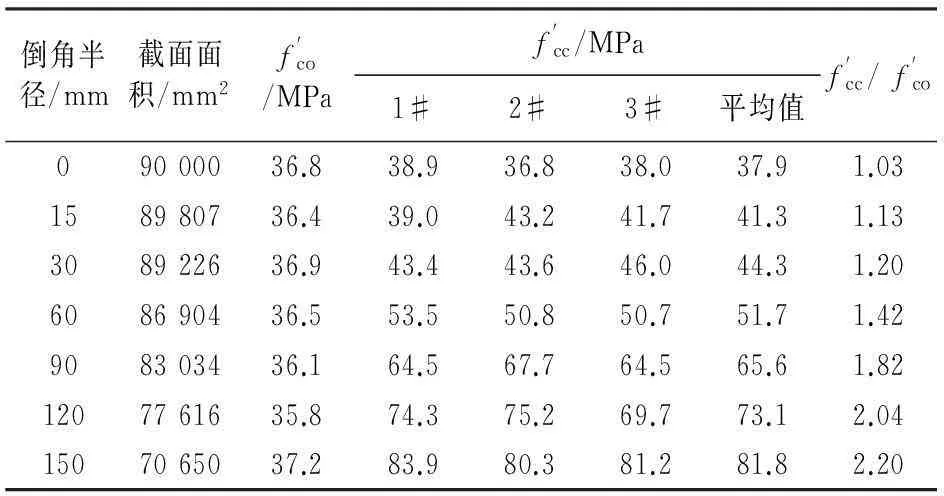
表2　CFRP约束混凝土抗压强度

应变/%

对于方柱，加固柱与未加固柱的应力-应变关系很接近.因此，如果不采取倒角措施，外包CFRP对混凝土方柱的承载力几乎没有提高作用，这与Wang 和 Wu[7]以及Mirmiran等[4]的研究成果一致，即可以认为这一结论不受尺寸效应的影响.但外包增强层大大改善了混凝土柱的延性，增强柱的纵向极限变形达到0.8%，这对于提高混凝土柱的变形能力极为有利.

总的来看，外包CFRP增强可以有效提高方柱的变形能力，但其增强效果并没有随着rc的增加成比例地递增，而且其增强效果远不如对承载能力的提高效果.例如，当rc从0.4逐步提高到0.8时，抗压强度增幅超过80%，而轴向极限应变变化很小.

2.3倒角半径的影响

对于方柱，倒角半径的大小对于外包CFRP的约束效应有重要影响，采用约束柱与对比柱抗压强度的比值fcc′/fco′可以定量分析倒角半径对增强效果的影响.从表2可以看到，对于直角方柱，fcc′/fco′仅为1.03，抗压强度几乎没有得到提高.fcc′/fco′最大者为圆柱，达到了2.20.

本文试验与文献[7]中的试验在尺寸上具有很好的对应关系，但除了尺寸差异外，两者在混凝土的抗压强度、CFRP的性能与约束量等方面存在或多或少的差异.为了突出研究尺寸差异对试验结果的影响，作者采用Mirmiran等[3]提出的约束效应比MCR的概念，定义为：

(2)

式中:fl为FRP提供的侧向约束应力;fco′为无约束混凝土的轴心抗压强度，注意到2r/b也就是倒角半径比rc.按照公式(2)计算得到的MCR考虑了约束程度、混凝土差异的影响.Mirmiran根据其试验结果，认为当MCR<0.15时，FRP对方柱的增强效应可以忽略.

图5给出了文献[7]与本试验的所有数据点及每组试件的平均值曲线.从图中可以看到，对于本试验的大尺寸试件，在试验范围内，随着MCR的增加，约束试件的抗压强度几乎成线性增长.这一倒角半径的影响规律与文献[7]中进行的4组小尺寸试件的试验结果基本一致.显然，Mirmiran提出的MCR=0.15为FRP对方柱的增强效应的界限值的结论，与试验结果不相符.

文献[7]的试验结果中，与本试验条件最为接近的一组为C30-2(C30强度等级的试件外包2层CFRP)，两条平均值曲线较为吻合，意味着MCR相同时，两者对于混凝土方柱的增强效果接近，试验结果具有可比性.应该注意到，相对于边长为150 mm的小试件，本试验300 mm边长的大试件即使多外包一层CFRP，在相同的rc下，其MCR大大低于小试件，表明试件的尺寸对CFRP的约束效应有重要影响.

MCR

2.4应变分布

试验中，在每个试件的中间截面上粘贴了应变片，以测量关键部位CFRP的应变.表3给出了这些点达到破坏状态时的应变值，各点数值均为每组试件对应部位测试数据的平均值，其中，Rmax为每一组试件达到破坏状态时，测得的M，C和T中的最大者与CFRP小试件单向拉伸试验测得的极限应变的比值.由表3可知，Rmax的最大值为0.724，从所有试件的统计结果来看，绝大部分试件达到破坏状态时，测得的CFRP极限应变低于其材性试验测得的极限应变的35%以上.对比文献[7]试验中与本文MCR接近的试验数据(C30的试件外包2层CFRP)，该组数据的Rmax最大为0.88，且多数试件CFRP的极限应变比CFRP材性试验测得的极限应变降低25%.试件外包CFRP的极限应变低于材性试验测得的极限应变，这一现象在许多研究者的论文中都进行过描述和讨论，一般认为造成这种现象的原因有两点：一是在加载过程中，核心区混凝土的局部开裂导致FRP的拉伸应力分布不均匀；二是外包FRP在倒角部位有一定的弯曲变形，特别是对于小倒角半径试件，产生显著的应力集中[5,7,14,17].从本试验与文献[7]的试验结果对比分析可知，大尺寸试件的应力集中现象更为显著，在试验范围内，试件尺寸增大一倍，外包CFRP的极限应变降低约10%，存在明显的尺寸效应.这也意味着实际结构中，FRP加固柱的延性很可能显著低于小试件测得的结果.

表3　CFRP的破坏应变

考虑到方形截面的对称性，选取1/4截面，将破坏状态时的M,C和T的极限应变表示出来，并将最大应变标在其相应位置，如图6所示.图中清楚显示出最大拉伸应变均出现在倒角中点(C点)或起点(T点)，与CFRP破坏的拉断位置基本吻合.与Wang和Wu的试验比较，CFRP没有在试件中部(M点附近)出现断裂的情况，由此可以推断，由倒角引起的FRP应力集中及其对试件破坏的影响程度，大尺寸试件要大于小尺寸试件，存在尺寸效应问题.

按照试件的应力-应变曲线是否出现下降段，试件可以分弱约束和强约束两类，rc=0.4是本试验的分界点.表4给出了3组弱约束试件在峰值应力时，对应CFRP在M，C和T点的应变平均值，其中，R1max为峰值应力时应变与小试件材性试验获取的极限应变值的比值，rmax为其与试件破坏时的最大应变值的比值.可以看到，各组试件的rmax和R1max都不大，特别是对于无倒角处理的试件， CFRP在荷载峰值时，其关键点C的拉伸应变仅为其破坏时应变的0.2，或其材料抗拉性能的0.1.这从约束机理上表明，外包CFRP不可能有效提高直角试件的承载力，这一结论与文献[7]中小尺寸试件的试验结果相同.对于弱约束试件，进入下降段后，CFRP的约束效应逐渐增大，试件破坏点的应变较峰值荷载对应的应变大很多，这种约束效应对试件的延性改善有显著贡献，但对试件增强的影响要有限得多，如图4所示.

图6　应变分布图

3理论模型与试验结果的对比

不少研究者提出了FRP约束方形(矩形)截面柱的约束模型，本文选用其中具有代表性的5种强度模型对本文试验柱进行计算分析：Mirmiran 等[4]，Lam等[5]，ILki等[18]，Kumutha等[19]和Wu等[20].在计算中，需要定义模型中FRP的失效条件，按照ILki等[18]的分析，FRP破坏应变取为其材性试验获取的极限应变的0.7倍.计算结果见表5，图7给出了各强度模型计算结果与本文试验结果的对比曲线.

表4　峰值应力处的应变比

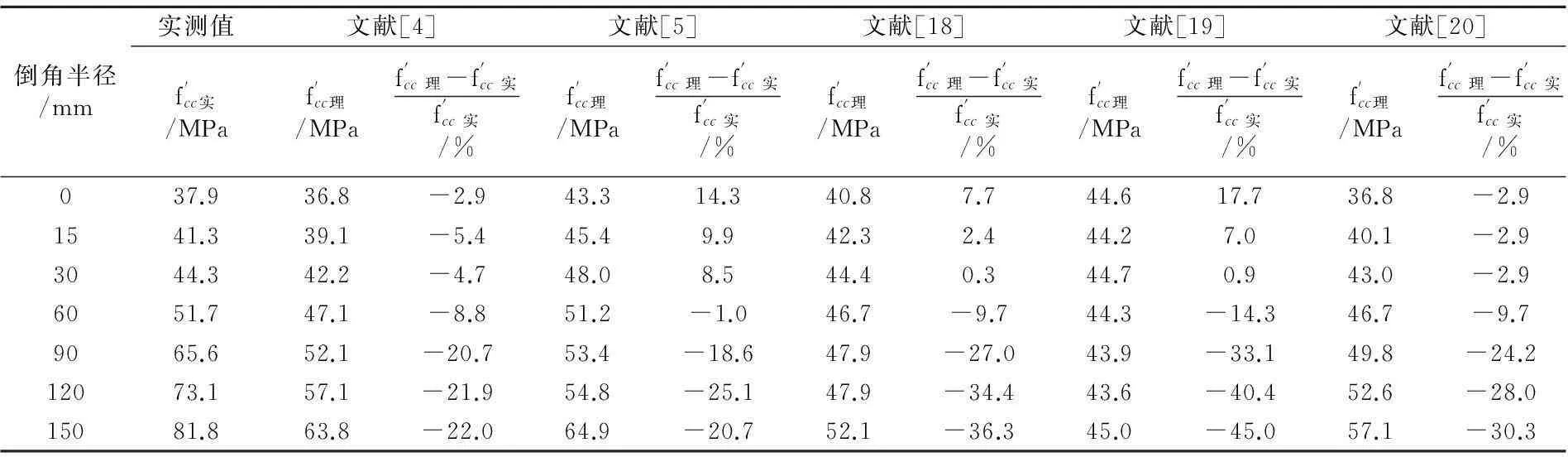
表5　理论模型与试验结果对比

2r/b

由图7可知，在倒角半径比较小的情况下(rc≤0.2)，文献[4]和文献[20]中强度模型预测的结果与试验数据吻合情况较好，而其他模型则明显高估了约束柱的抗压强度，且对于直角试件，这些模型的计算结果体现出较为明显的约束效应，与试验结果明显不相符.在倒角半径比较大的情况下(rc>0.2),所有强度模型都低估了试件的抗压强度，且预测误差随着rc的增大而显著增大.整体来看，在所有强度模型中，文献[4]中模型的预测结果与试验结果最为接近，但相对误差也不小，在-2.9%～-22.0%之间.比较特殊的是文献[20]中的模型，该模型是基于文献[7]的试验结果提出的，试件尺寸为150 mm×150 mm×300 mm，该模型对他们自己的试验结果吻合情况很好，因此，有必要考虑尺寸效应的影响.而与本文试验数据相比较，模型的预测值显著低于试验值，这与尺寸效应对抗压强度的一般影响规律不相符，这种差异可能来自于两方面：一是本文试验材料和条件与文献[7]中的试验存在一定差别；二是本文试件尺寸显著增大，约束程度显著低于文献[7]中的试验，而低约束程度相对于高约束程度，其对于强度的增强效果相对更显著，因此，基于较强约束程度提出的文献[20]模型预测本试验结果可能会偏低.而对于FRP约束柱的尺寸效应研究来说，本试验试件尺寸仍很有限，且数据量也很有限，尺寸效应的影响还需要进一步的试验研究和分析.

4结论

本文通过对7组逐步变化倒角半径的大尺寸CFRP约束混凝土方形柱进行轴心抗压试验，获取了基本力学性能，并与已有小试件结果进行了比较分析，得到以下主要结论：

1)在试验范围内，约束柱的抗压强度比fcc′/fco′随倒角半径比的增加几乎呈线性增加，倒角半径对CFRP约束方柱的力学性能有重要影响.

2)本试验所进行的大尺寸CFRP约束柱试验，破坏模式均为外包CFRP被拉断，且破坏位置均在倒角范围内，具有显著的应力集中现象.试件破坏时，CFRP的最大应变低于材性试验所测得极限应变的35%以上，明显大于已有小试件的试验结果，具有较为显著的尺寸效应.

3)采用约束效应比MCR，将本试验的大尺寸试件与已有的小尺寸试件试验结果建立起较好的对应关系，反映出尺寸效应的影响.试件的尺寸增加，大大降低了外包FRP的约束效应.

4)对于小倒角试件，特别是直角试件，达到应力峰值时，CFRP的约束效应很低，增强效应可以忽略；进入下降段后，CFRP的约束效应逐渐显现，对增加试件的延性有显著作用.

5)采用现有CFRP约束方形柱的强度模型对试验结果进行了对比，模型的预测结果与试验结果在rc较大的情况下存在显著差异，有必要考虑尺寸效应的影响，这方面的研究需要进行进一步的试验和分析.

参考文献

[1]徐竞雄. FRP加固矩形混凝土柱研究[D]. 武汉：华中科技大学土木工程与力学学院, 2011：1-4.

XU Jing-xiong. Study on FRP confined rectangular concrete columns[D]. Wuhan: School of Civil Engineering & Mechanics, Huazhong University of Science & Technology, 2011:1-4.(In Chinese)

[2]TENG J G, CHEN J F, SMITH S T,etal. Behaviour and strength of FRP-strengthened RC structures: a state-of-the-art review[J]. Proceedings of the ICE-Structures and Buildings, 2003, 156(1): 51-62.

[3]滕锦光，陈建飞，史密斯S T，等. FRP加固混凝土结构[M]. 北京：中国建筑工业出版社, 2005：185-195．

TENG Jin-guang, CHEN Jian-fei, SMITH S T,etal.FRP strengthened RC structures[M].Beijing: China Architecture & Building Press, 2005：185-195. (In Chinese)

[4]MIRMIRAN A, SHAHAWY M, SAMAAN M,etal. Effect of column parameters on FRP-confined concrete[J]. Journal of Composites for Construction, 1998, 2(4): 175-185.

[5]LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete in rectangular columns[J]. Journal of Reinforced Plastics and Composites, 2003, 22(13): 1149-1186.

[6]LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete[J]. Construction and Building Materials, 2003, 17(3):471-489.

[7]WANG L M, WU Y F. Effect of corner radius on the performance of CFRP-confined square concrete columns: test[J]. Engineering Structures, 2008, 30(2): 493-505.

[8]吴刚, 吕志涛. 纤维增强复合材料(FRP)约束混凝土矩形柱应力-应变关系的研究[J]. 建筑结构学报, 2004, 25(3):99-106.

WU Gang, LV Zhi-tao. Study on the stress-strain relationship of FRP-onfined concrete rectangular columns[J]. Journal of Building Structures, 2004, 25(3):99-106. (In Chinese)

[9]魏洋, 吴刚, 吴智深,等. FRP约束混凝土矩形柱有软化段时的应力-应变关系研究[J]. 土木工程学报, 2008, 41(3):21-28.

WEI Yang, WU Gang, WU Zhi-shen,etal. Study on the stress-strain relationship for insufficient FRP-confined rectangular concrete columns[J]. China Civil Engineering Journal, 2008, 41(3):21-28. (In Chinese)

[10]陆新征, 冯鹏, 叶列平. FRP布约束混凝土方柱轴心受压性能的有限元分析[J].土木工程学报, 2003, 36(2):46-51.

LU Xin-zheng, FENG Peng, YE Lie-ping. Behavior of FRP-confined concrete square columns under uniaxial loading[J].China Civil Engineering Journal, 2003, 36(2):46-51. (In Chinese)

[11]刘涛, 冯伟, 张智梅,等. 碳纤维布约束混凝土矩形柱的抗压性能研究[J].土木工程学报, 2006, 39(12):41-47.

LIU Tao, FENG Wei, ZHANG Zhi-mei，etal. A study on the compressive performance of rectangular concrete columns confined with CFRP sheets[J]. China Civil Engineering Journal, 2006, 39(12):41-47.(In Chinese)

[12]王代玉, 王震宇, 乔鑫. CFRP 中等约束钢筋混凝土方柱反复受压本构模型[J]. 湖南大学学报: 自然科学版, 2014, 41(4): 39-46.

WANG Dai-yu, WANG Zhen-yu, QIAO Xin. Cyclic stress-strain model for CFRP moderately-confined reinforced concrete square columns.[J]. Journal of Hunan University:Natural Sciences,2014, 41(4): 39-46. (In Chinese)

[13]ROCHETTE P, LABOSSIERE P. Axial testing of rectangular column models confined with composites[J]. Journal of Composites for Construction, 2000, 4(3): 129-136.

[14]PESSIKI S, HARRIES K A, KESTNER J T,etal. Axial behavior of reinforced concrete columns confined with FRP jackets[J]. Journal of Composites for Construction, 2001, 5(4): 237-245.

[15]ROCCA S. Experimental and analytical evaluation of FRP-confined large size reinforced concrete columns[D]. Rolla: University of Missouri-Rolla, 2007：1-16.

[16]WANG Z, WANG D, SMITH S T,etal. CFRP-confined square RC columns. I: experimental investigation[J]. Journal of Composites for Construction , 2012, 16(4) : 150-160.

[17]LAM L, TENG J G. Stress-strain models for concrete confined by fiber-reinforced polymer[C]//Advances in Mechanics of Structures and Materials, Proceedings of the 17th Australasian Conference.Lisse, The Netherlands: AA Balkema Publishers,2002: 39-44.

[18]ILKI A, KUMBASAR N, KOC V. Low strength concrete members externally confined with FRP sheets[J]. Structural Engineering & Mechanics, 2004 (18): 167-194.

[19]KUMUTHA R, VAIDYANATHAN R, PALANICHAMY M S. Behaviour of reinforced concrete rectangular columns strengthened using GFRP[J]. Cement and Concrete Composites, 2007, 29(8): 609-615.

[20]WU Y F, WANG L M. Unified strength model for square and circular concrete columns confined by external jacket[J]. Journal of Structural Engineering, 2009, 135(3): 253-261.

Experimental Research on Large-scale Square Columns Confined with Wrapped CFRP under Axial Compressive Load

SHAN Bo1†, CAI Jing1, XIAO Yan1,Giorgio Monti1,2

(1.College of Civil Engineering, Hunan Univ, Changsha,Hunan410082, China; 2. Univ of Rome Sapienza, Rome00917, Italy )

Abstract:Although the size of specimens presents significant effect on the mechanical performance of CFRP confined concrete columns, the size effect is a blank area of study until now. Based on a series of tests on seven groups of Carbon Fibre Reinforced Plastics (CFRP) confined large-scale square concrete columns with different corner radius, the basic mechanical properties were obtained, such as the failure modes, compressive strengths, stress-strain relationships, and the ultimate strain distribution of CFRP jacket. Moreover, their comparison with the experimental results of the smaller-scale specimens has been investigated and published. It is demonstrated that the confined strength increases with the increase of the corner radius except for the specimens with sharp corner. All of the specimens fail due to CFRP rupture, and the fracture location occurs in the chamfer zone. Meanwhile, the phenomenon of the stress concentration is obvious. The confinement ratio, i.e., MCR, shows a certain correlation with the size of specimen on the compressive strength of CFRP confined specimens. The ultimate strains measured on the CFRP jackets are about 35% less than that tested by the coupon specimens, while it is more serious than that for the smaller-scale specimens. It is found that the discrepancies between the predicted results of the existing strength models of CFRP confined square column and the experimental results in this work are obvious. It suggests that the size effect on the FRP confined square columns cannot be ignored,which needs to be further researched.

Key words:FRP；confinement; columns; axial compression; size effect

中图分类号：TU375.3

文献标识码：A

作者简介：单波(1976-)，男，湖南益阳人，湖南大学副教授，工学博士†通讯联系人，E-mail:supershanb@hnu.edu.cn

基金项目：国家重点基础研究发展计划(973计划)资助项目( 2012CB026204)；国家自然科学基金资助项目(51278180)，National Natural Science Foundation of China(51278180)

*收稿日期：2015-03-26

文章编号：1674-2974(2016)03-0075-08