不同倒角半径方柱绕流数值模拟研究

张志超，杨汉彬

(西南交通大学土木工程学院，四川成都 610036)

钝体绕流(尤其是方形柱体绕流)是流体力学的经典问题之一。当流体以一定速度流经柱体结构时，流体会在结构后方产生规则的旋涡脱落，即卡门涡街现象。方形截面是典型的柱体截面形式之一，但工程中也存在方形带倒角的截面形式，如各种大型桥梁的桥墩、高桩码头、高层建筑的立柱等。到目前为止，许多学者对方柱绕流问题进行了研究，Lyn等[1]对雷诺数Re=21400的方柱绕流流场特性进行了详细的研究，给出了流动速度及其脉动量的分布，为数值模拟提供了事实依据和考核标准。秦浩等[2]对高雷诺数下方柱绕流问题进行了PIV(Particle Image Velocimetry)试验和二维数值模拟，研究表明通过PIV试验可准确观测到方柱尾流的整个脉动流场且γ-Reθ模型对方柱绕流流场的模拟十分准确。付英男等[3]对方柱绕流进行了三维数值模拟，发现Re=100、300时方柱绕流存在三维特性，导致三维数值模拟计算的阻力系数和升力系数均小于二维计算结果。李雪健等[4]对方柱绕流进行了二维和三维数值模拟，结果发现三维数值模拟优于二维数值模拟且随着雷诺数的增加，Cd的平均值增加而St先增大后减小。王远成等[5]采用RNGk-ε湍流模型对方柱绕流流场进行了数值模拟，结果表明RNGk-ε湍流模型可以成功模拟绕方柱的不稳定，非定常和剧烈分离流动。朱梦楠等[6]对单个方柱及间距为1H，2H，3H的两并列方柱的流动进行了数值模拟，研究发现当两并列方柱之间的间距为2H时，方柱壁面处的升阻力会发生突变，间距为3H时，两并列方柱绕流数值模拟的结果与单方柱绕流的结果类似。周强等[7]对高雷诺数下方柱绕流进行了三维数值模拟，结果表明：雷诺数为22 000下方柱尾流区回转长度为1.37倍方柱宽带，St为0.121，脉动升力系数为1.40，展向长度取8倍方柱宽带可更准确地获得三维湍流特性；沈立龙等[8]等人对亚临界区圆柱和方柱绕流进行了数值模拟，发现同一雷诺数下圆柱绕流阻力系数较方柱绕流阻力系数要小，但圆柱的Strouhal数较方柱的要高，单圆柱和单方柱绕流生成的旋涡脱落周期不同，方柱的偏大，二者的旋涡脱落特性与流场运动具有相似特性。圆柱的分离点随着雷诺数的增大而逐渐向柱后方推移，方柱的分离点则固定在柱前两个棱角位置。虽然之前对方柱绕流问题进行了很多研究，但对于带倒角方柱的研究却很少，杜明倩等[9]采用数值模拟的方法对不同倒角半径下方柱绕流进行了二维数值模拟，研究发现增加倒角半径会改变方柱的分离点，使尾流区长度增加，旋涡尺度减小，柱体截面越接近圆形，斯托罗哈数会逐渐增大。Kumar等[10]使用粒子图像流速测量技术(PIV)，研究了不同倒角半径的流场特性，发现当倒角半径越大时，尾流附近旋涡脱落越均匀。

本文运用CFD软件、基于k-ωSST模型对亚临界区Re=22000的单方柱和倒角半径为0.15D、0.25D和0.35D的方柱进行了三维数值模拟，计算得到这几种情况下的升阻力系数、斯特罗哈数等重要动力学参数，并对圆柱、方柱和带倒角方柱绕流机制进行了分析。

1 控制方程与建模

1.1 控制方程

不可压缩粘性流体的运动可用Navier-Stokes方程来描述，连续性方程与动量方程分别为：

式中：ui，uj为速度分量；p为压力；ρ为流体的密度；v为流体的动力粘性系数。

对于湍流情况，本文采用k-ωSST模型，该模型综合了k-ω模型在近壁区计算的优点和k-ε模型在远场计算的优点，将k-ω模型和标准k-ε模型都乘以一个混合函数后再相加就得到这个模型。在近壁区，混合函数的值等于1，因此在近壁区等价于k-ω模型。在远离壁面的区域混合函数的值则等于0，因此自动转换为标准k-ε模型。与标准k-ω模型相比，k-ωSST模型中增加了横向耗散导数项，同时在湍流粘度定义中考虑了湍流剪切应力的输运过程，模型中使用的湍流常数也有所不同。这些特点使得k-ωSST模型的适用范围更广，如可以用于带逆压梯度的流动计算、翼型计算、跨音速激波计算等。模型方程如下：

(3)

(4)

式中：k为湍流动能，ω为湍流比耗散率，σω2=0.856，β*=0.09，混合函数`定义如下：

(5)

(6)

式中：y表示距离壁面的距离，CDkω代表比耗散率输运方程中交错扩散项的正值部分，涡粘系数定义为

(7)

式中：a1=0.31，Ω为涡量，混合函数F2定义如下：

(8)

模型中常数的取值为OpenFOAM中的默认值。

1.2 参数定义

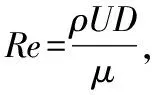
1.3 边界条件和初始条件设置

计算流场的边界条件和初始条件设置如下：

初始条件：初始设定一个从左向右的速度场，u=U0=0.22m/s，v=0，w=0；其中，u、v和w分别为x、y和z方向的速度，方柱边长D=0.1m。

边界条件：来流方向为均匀流速U0，出口为自由出流，方柱采用无滑移固壁边界，其余边界采用对称边界(图1)。

(a)XY方向计算域示意

(b)Z方向计算域示意

网格划分采用六面体结构化网格，方柱壁面处y+取20，具体网格划分如图2所示。

(a)方柱

(b)倒角0.15D

(c)倒角0.25D

(d)倒角0.35D

2 计算结果分析

2.1 升阻力系数

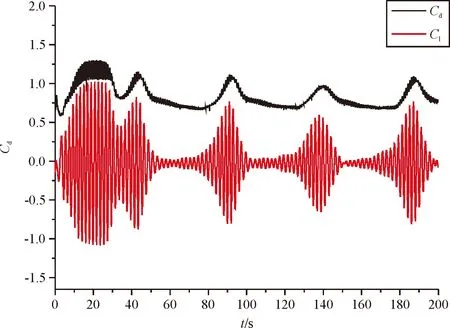
图3为利用OpenFOAM软件模拟Re为22 000时方柱和倒角半径为0.15D，0.25D和0.35D方柱阻力系数Cd及升力系数Cl随时间t变化。

由图3(a)可以看出，单方柱的阻力系数和升力系数在20s附近开始稳定，阻力系数稳定在2.12，升力系数在-1.92到1.92之间波动。当倒角半径增大到0.15D时，方柱的升力系数和阻力系数都开始减小且阻力系数降低约46 %，而后当倒角半径继续增加时，方柱的阻力系数继续减小，升力系数变化不大，当倒角半径为0.35D时，阻力系数相对于倒角半径为0.25D时无明显变化，但升力系数却开始增大。

表1为三维计算结果与实验及以往文献结果的对比，结果显示，Re=22000时的模拟结果能很好的与参考文献中数据相吻合，即说明本文模拟结果的正确性。

2.2 斯托罗哈数

斯托罗哈数又被称为涡脱落的无量纲频率。根据模拟所得结果绘制了Re=22000时单方柱和倒角半径为0.15D、0.25D和0.35D方柱绕流的St随倒角半径的变化曲线如图4所示。

(a)方柱

(b)倒角半径0.15D

(c)倒角半径0.25D

(d)倒角半径0.35D

由上图可知，单方柱的St为0.124，当倒角半径增大到0.15D时，St以较快速度增大到0.212，当倒角半径继续增大时，St的增速变得平缓，说明方柱增加倒角后，旋涡脱落频率

表1 Re=22 000时单方柱绕流模拟计算结果

图4 方柱绕流的斯托罗哈数随倒角半径变化曲线

会加快，脉动更强，这也与文献[9]中的结果相一致。

2.3 三维涡量图

方柱及倒角半径为0.15D、0.25D和0.35D方柱的三维涡量图如图5所示。

(a)方柱

(b)倒角半径0.15D

(c)倒角半径0.25D

(d)倒角半径0.35D

从上图可以看出，由于方柱具有固定的分离角，其旋涡脱落在高度方向一致，而带倒角方柱具有明显的胞体结构，呈现明显的三维特征。由于胞体结构的存在说明其旋涡脱落的相关性较弱，这也是导致其阻力系数小于方柱的原因之一。

2.4 边界层分离

亚临界区雷诺数下方柱绕流边界层分离为层流分离，且边界层内液体运动时会伴有能量损失，本次模拟的方柱雷诺数Re=22000，正好处于亚临界区。对于圆柱见图6(a)，随着雷诺数的增大，分离点会逐渐向后推移。在压强最大的P点至柱上下A、B两点的边界层内液流处于加速减压状态，在A、B两点时压强最小，流速最大，在这两点之后液流处于减速增压状态，当动能减小至零无法提供压能时，完成分离。对于方柱见图6(b)分离点固定在柱前的两个棱角位置。而对于带倒角方柱见图6(c)分离点则相对复杂，其分离点介于圆柱和方柱之间。

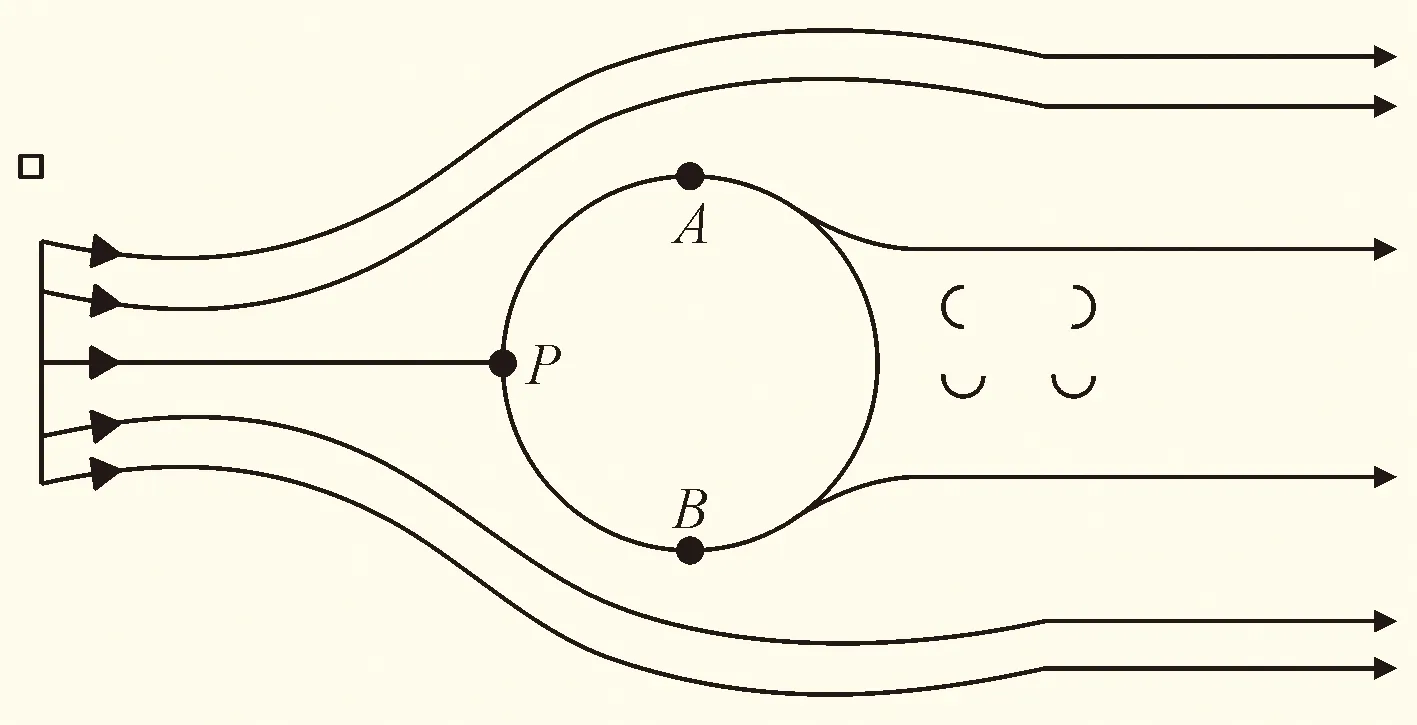
(a)圆柱

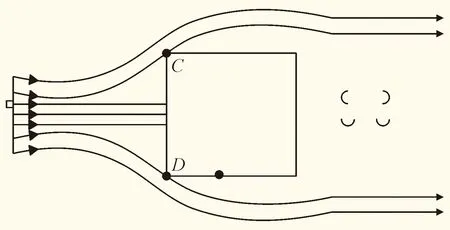
(b)方柱

(c)带倒角方柱

3 结论

本文运用OpenFOAM软件，通过对亚临界区Re=22000下单方柱和倒角半径为0.15D、0.25D和0.35D的方柱进行了数值模拟，得出以下结论：

(1)Re=22000时，单方柱的升力系数和阻力系数最大，随着倒角半径的增加，升阻力系数会减小，但当倒角半径为0.35D时，升力系数相对于倒角半径半径为0.15D和0.25D时会增加，但始终小于方柱的升力系数。

(2)带倒角方柱的三维数值模拟会出现胞体结构，呈现明显的三维特性，柱体高度方向旋涡脱落的相关性较弱。

(3)在一定范围内，带倒角方柱的斯托罗哈数会随着倒角半径的增大而逐渐增大。

(4)单方柱绕流存在固定的分离点，即柱前两个棱角的位置，当方柱出现倒角后，方柱的分离点发生改变，不再固定在之前的棱角位置，而是介于圆柱和方柱之间。随着倒角半径的增大，带倒角方柱的流动特性越来越近似于圆柱。