用格子Boltzmann方法模拟方柱绕流

谢晨 李银山 霍树浩

摘要 基于格子Boltzmann方法的原理和对边界条件处理的便捷性，分别对单方柱和并列双方柱绕流进行了研究。对于单方柱绕流，分别研究了不同雷诺数和阻塞比对它的影响，给出了不同雷诺数下单方柱绕流的流线图和涡量图，以及平均阻力系数和最大升力系数随雷诺数的变化曲线，得到单方柱产生卡门涡街的临界雷诺数，也给出了不同阻塞比下单方柱绕流的涡量图，以及不同阻塞比对平均阻力系数和最大升力系数所产生的影响。对于并列双方柱绕流，研究了不同间距比对它的影响，给出了不同间距比下的并列双方柱绕流的流线图和涡量图，得到了流动从偏流型向对称型转换的临界间距比以及使得两个方柱后的涡流互相影响最为明显的间距比。

关 键 词 格子Boltzmann方法;方柱绕流;雷诺数; 阻塞比;间距比

Abstract Based on the lattice Boltzmann method and the convenience of the boundary condition processing， the flow past a single square cylinder and the parallel square cylinder were studied respectively. For the single square cylinder flow， the effects of different Rayleigh numbers and blocking ratios on it are studied separately， the streamline diagram and vorticity diagram of the flow around a single square cylinder under different Rayleigh numbers， and the variation curve of the average drag coefficient and the maximum lift coefficient with the Rayleigh number are given. The critical Rayleigh number of the Karman vortex street generated by the single square cylinder is obtained. The vorticity diagrams of the flow around a single square cylinder with different blocking ratios and the effects of different blocking ratios on the average drag coefficient and the maximum lift coefficient are also given. For the parallel flow around the two square cylinder， the influence of different spacing ratios on the flow is studied. The flow diagram and vorticity diagram of the flow around the two square cylinder at different spacing ratios are given， and the flow from the bias flow to the symmetrical conversion is obtained. The eddy currents behind the two square cylinder affect each other's most obvious spacing ratio.

Key words lattice boltzmann method; flow past square cylinder; reynolds number;blocking ratio; spacing ratio

0 引言

鈍体绕流广泛存在于实际生活中，例如流体经过桥墩或者海洋平台等。柱体绕流是钝体绕流的经典问题之一，在流体经过柱体时，由于柱体的阻碍作用，在柱体后面会产生涡，而柱体后面的涡会对柱体产生很大的破坏力，当流体的速度达到某个临界值时，在柱体后面就会出现卡门涡街。由于这类问题在工程上的重要性，所以越来越多的人开始研究柱体绕流。

许多人用数值模拟或者试验的方法来研究不同的柱体绕流问题，其中数值模拟不失为一种有效的手段，如周强等[1]用LES方法对单方柱绕流进行了模拟;Okajima A[2]用有限差分法对单方柱绕流进行了模拟;程维贤等[3]用有限元模拟单方柱和串列双方柱绕流;陈素琴等[4]用 MAC方法对并列双方柱绕流进行了模拟。格子Boltzmann方法的思路和传统的模拟流体的方法完全不同，它用粒子群来代替流体，粒子流沿着给定的方向迁移并在格子节点处发生碰撞重整，再对每个粒子新得到的分布函数进行统计，得到密度和速度等宏观变量，求得的宏观物理量能够满足宏观偏微分方程[5-6]，对于复杂边界条件[7-12]的问题处理起来相对容易，只需要简单的算法就可以在计算机上实现并行[13]计算，具有更高的计算效率。本文对单方柱和并列双方柱绕流进行了模拟，得到了不同雷诺数和阻塞比对单方柱绕流的影响以及两方柱之间的间距比对并列双方柱绕流造成的影响。

1 格子Boltzmann方法

格子Boltamann方法是由McNamara和Zaretti在1988年引入，用于克服格子气自动机的缺点，从此，格子Boltzmann方法称为一种求解流体动力学问题的功能强大的替代方法。格子Boltzmann方法可视为一种显示方法，编程容易，并行性也很好。

2 格子Boltzmann方法的边界格式处理

流体运动总会涉及到边界条件，格子Boltzmann方法边界处理格式有很多种，本文根据问题所给边界用到非平衡态反弹格式和非平衡态外推格式这2种边界处理方式。

2.1 非平衡态外推格式边界

非平衡态外推格式边界的核心是将边界节点a上的分布函数分成平衡态和非平衡态两部分，其中平衡态部分根据边界条件的定义近似得到，非平衡态部分则用流体相邻节点b处的非平衡态部分代替。表达式如下：

2.2 非平衡态反弹格式边界

3 方柱绕流模拟

3.1 单方柱绕流模拟

3.1.1 物理模型及边界条件

从图2中可以看出计算区域为45D×15D，其中D为方柱边长，入口速度为均匀来流U = 0. 1。其中方柱的特征尺寸D取8个格子单位，管道水平和竖直方向分别划分为360和120个格子单位。入口和出口分别采用速度和压力边界，其他边界用的都是非平衡态外推格式边界。

3.1.2 利用格子Boltzmann方法估计柱体表面的力

利用格子Boltzmann方法估计柱体表面的力通常有2种办法，应力积分法[15]和动量交换法[16]。相比之下，动量交换法实现起来更加简单，直接用分布函数进行计算，特别适合于用在格子Boltzmann方法中，这也是格子Boltzmann方法区别于其他方法的特色之一。所以，本文用动量交换法来计算柱体表面的升力系数和阻力系数。

3.1.3 雷诺数对方柱绕流的影响

本文对雷诺数Re为10～300范围内的方柱绕流进行模拟，雷诺数定义为[Re=UDv]，其中[ν]为运动粘性系数。图3给出了不同雷诺数时方柱绕流的流线图，从图3可以看出，当Re = 10～89时，在方柱后缘发生流动分离现象，方柱后面产生一对对称的回流漩涡，随着雷诺数的增大漩涡也在逐渐扩大;当Re = 90时，尾流的对称状态破坏，开始出现漩涡脱落现象，因此，定常流失稳的临界Re在90左右。

图4为不同雷诺数下流场涡量云图。从图4可以看出，当Re比较小的时候，在方柱后面形成上下对称的涡，并且在一定范围内随着Re的增加涡在变长，此时流场是定常的。随着Re的持续增加，方柱后的涡开始脱落，当Re = 90时，方柱后面出现周期性摆动和交错的卡门涡街，此时流场变为非定常。当Re增加到300时，尾涡有了紊乱的趋势。

Re对平均阻力系数[Cdavg]和最大升力系数[Clmax]的影响如图5所示。当Re = 10～100时，平均阻力系数下降比较快，说明雷诺数在这个范围内的变化对平均阻力系数的影响比较大。此后，随着Re的增大，平均阻力系数下降的变的相对平缓，Re对平均阻力系数的影响变小。当Re = 10～89时，最大升力系数为0，由于此时雷诺数比较小，对最大升力系数的影响还不足以显现出来。此后，Re的变化对最大升力系数的影响慢慢凸显出来，即随着Re的增大，最大升力系数在逐渐变大。

3.1.4 阻塞比的影响

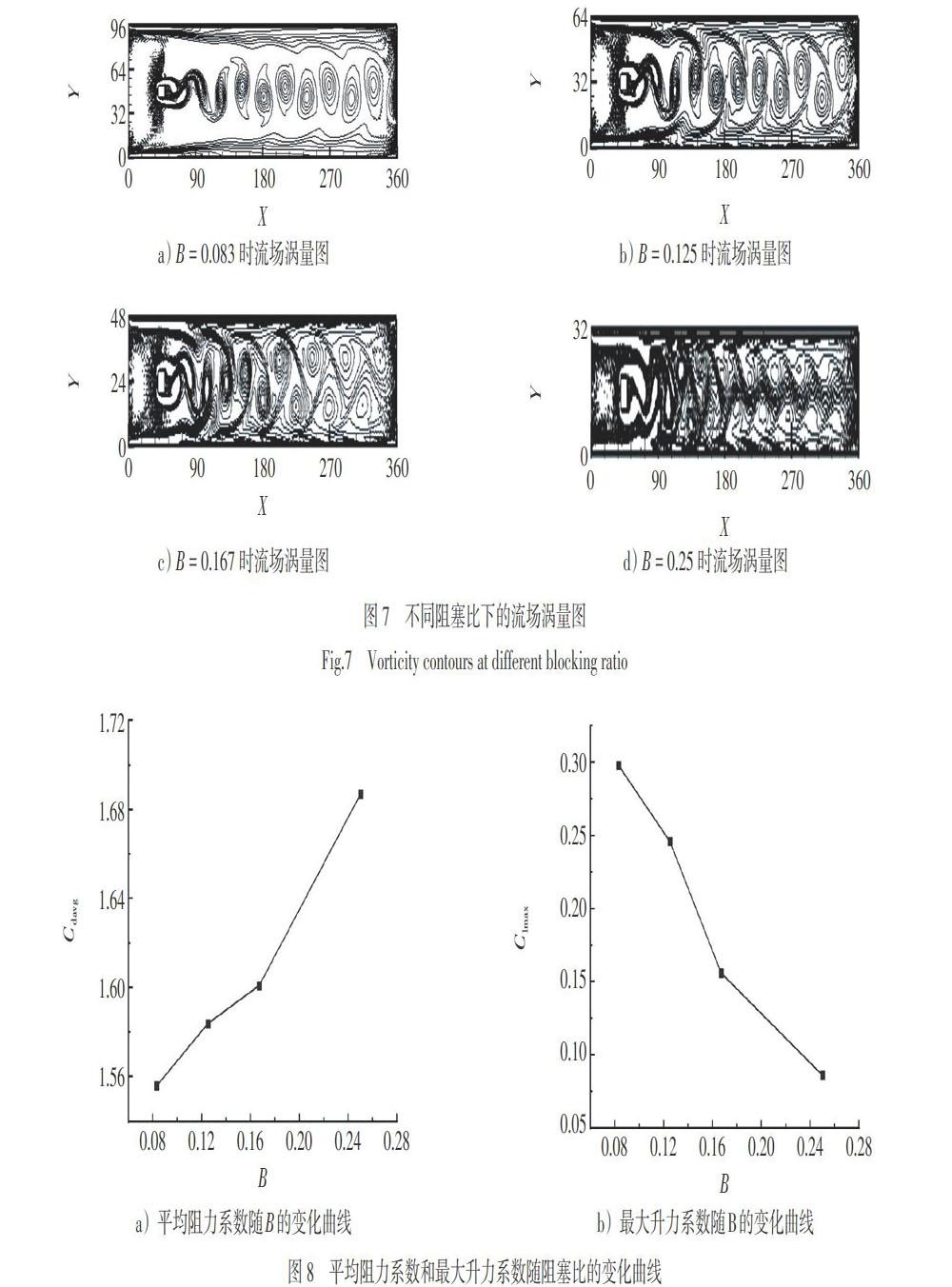
在研究阻塞比[B=DH]对方柱绕流的影响时，本文取Re = 200，除了改变阻塞比之外，其他条件不变。图7给出了阻塞比B为0.083、0.125、0.167和0.25的方柱绕流的涡量图。

由图7可见，当阻塞比较小时，如当B = 0.083时，此时壁面效应对涡脱落所产生的影响比较小，方柱后面的卡门涡街比较清楚、规则。随着阻塞比的增大，上下壁面附近开始出现小涡，这些小涡与方柱后面产生的大涡相混合，一同向下游运动;这种现象随阻塞比的增加越来越明显（图7c））;随着阻塞比进一步增加（图7d）），在方柱后形成了很长的回流区，涡脱落变得不再规则，刚刚脱落的大涡会立刻与壁面附近的小涡混合，尾迹里见不到明显的卡门涡街。

图8给出了方柱平均阻力系数和最大升力系数随阻塞比的变化曲线。由图可知，平均阻力系数随阻塞比增大逐渐增加，最大升力系数则隨阻塞比增大在逐渐减小。这是因为随着阻塞比的增大，上下边界与方柱越来越靠近，流体的流动受到影响，这就导致了柱体表面的阻力系数和升力系数发生改变。

3.2 双方柱绕流模拟

本文研究的是并列双方柱之间的间距S与方柱特征尺寸D的比值（间距比）对流场的影响。计算示意图如图9所示。

计算区域为60D × 18D，其中方柱的特征尺寸D取10个格子单位，管道水平和竖直方向分别划分为600和180个格子单位。与单方柱采用相同的边界条件，在Re = 200的条件下分别对并列方柱间距比S/D=0.2、S/D = 1.0、S/D = 1.4、S/D = 1.8、S/D = 2.0、S/D = 4.0这6种条件进行模拟。

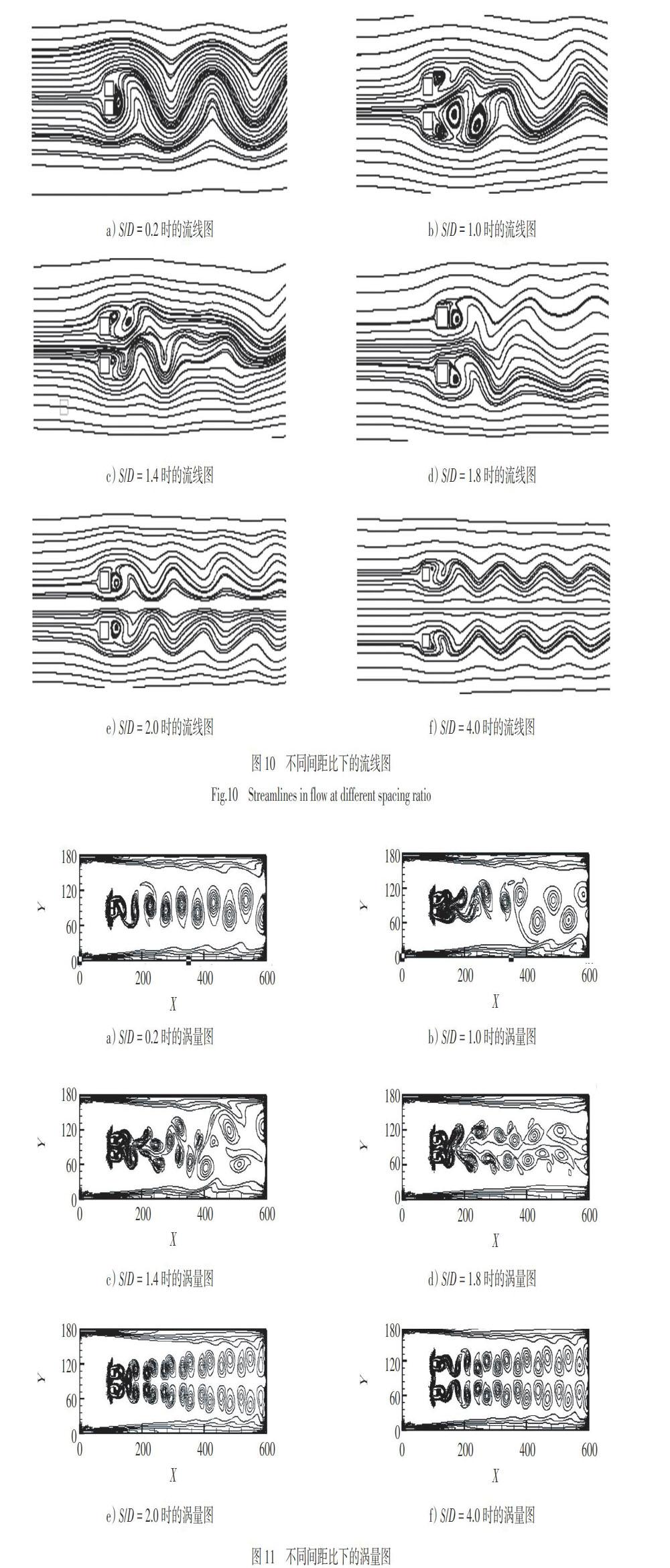
图10给出了6种不同方柱间距比下的流场流线图。从图10中可以看出，刚开始方柱间距很小，间隙流不足以影响方柱后方的流动状态，此时很难看到偏流现象，所以在方柱后方会形成共同的漩涡（图10a））。随着2个方柱之间的距离慢慢变大，2个方柱彼此之间的干扰在减弱，但是，间隙流对流场的影响开始显现出来，每个方柱后面都产生了各自的漩涡，并且把它们共同产生的漩涡缓慢的推离方柱后方（图10b）和图10c）），偏流现象已经出现。当间距比达到临界值S/D =1.8时，偏流现象消失（图10d）），间距比S/D >1.8时，2个方柱后面出现了对称的尾流（图10e）和图10f）），此时流场转变为对称流。

图11给出了6种不同方柱间距比下的流场涡量图。从图11中可以看出，当间距比较小S/D = 0.2时，2个方柱之间的影响较小，流场的特征和单方柱绕流相似;随着间距比的增加，流场开始变复杂，2个方柱后的漩涡也变的不规则;当间距比S/D = 1.4时，2个方柱的涡流彼此影响最明显;当间距比S/D > 1.8时，2个方柱各自形成的涡之间的影响越来越小，方柱后面形成2个反向同步脱落的涡街，每个方柱后面的涡形逐渐接近单方柱卡门涡街状态。

4 結语

本文利用格子Boltzman方法对单方柱和并列双方柱绕流进行了数值模拟。对于单方柱研究了雷诺数Re = 10～300范围内以及4种阻塞比即B = 0.083、0.125、0.167和0.25对单方柱绕流的影响，给出了不同雷诺数下单方柱绕流的流线图和涡量图，得到定常流失稳的临界Re和开始出现明显卡门涡街的Re在90左右，也得到了当Re = 10～300时平均阻力系数随Re的增大而减小，当Re = 10～89时，最大升力系数为0，此后，随着Re的增大，最大升力系数在逐渐变大。当阻塞比较小时，壁面效应对涡脱落所产生的影响比较小，方柱后面的卡门涡街比较清楚、规则，随着阻塞比的增大，上下壁面附近开始出现小涡，这些小涡与方柱后面产生的大涡相混合，一同向下游运动，这种现象随阻塞比的增加越来越明显，随着阻塞比的进一步增加，在方柱后形成了很长的回流区，涡脱落变得不再规则，刚刚脱落的大涡会立刻与壁面附近的小涡混合，尾迹里见不到明显的卡门涡街。也得到了平均阻力系数和最大升力系数都随阻塞比增大逐渐增加。对于并列双方柱研究了2个方柱之间的间距比对并列双方柱绕流的影响，给出了不同间距比下的流场流线图和涡量图，得到了间距比S/D = 1.8为流场由偏流转化为对称流的临界值，也得到了使得双方柱绕流的涡流彼此影响最为明显的间距比为S/D = 1.4。

参考文献：

[1]    周强，廖海黎，曹曙阳. 高雷诺数下方柱绕流特性的数值模拟[J]. 西南交通大学学报，2018，53（3）：533-539.

[2]    OKAJIMA A. Numerical simulation of flow around rectangular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics，1990，33（1/2）：171-180.

[3]    穆维贤，赖国璋. 方柱和双方柱绕流的数值模拟[J]. 水动力学研究与进展（A辑），1990，5（4）：76-80.

[4]    陈素琴，顾明，黄自萍. 两并列方柱绕流相互干扰的数值研究[J]. 应用数学和力学，2000，21（2）：131-146

[5]    HE X Y，LUO L S. Lattice boltzmann model for the incompressible navier-stokes equation[J]. Journal of Statistical Physics，1997，88（3/4）：927-944.

[6]    MCNAMARA G R，ZANETTI G. Use of the Boltzmann equation to simulate lattice gas automata[J]. Physical Review Letters，1988，61（20）：2332-2335.

[7]    王露，李天匀，朱翔，等. 基于改进的浸没边界-格子Boltzmann方法的圆柱绕流仿真计算[J]. 中国造船，2017，58（4）：150-159.

[8]    顾娟，黄荣宗，刘振宇，等. 一种滑移区气体流动的格子Boltzmann曲边界处理新格式[J]. 物理学报，2017，66（11）：220-228.

[9]    任晓飞，魏守水，刘飞飞，等. 改进的浸入边界-晶格Boltzmann法的蠕动流分析[J]. 振动. 测试与诊断，2018，38（3）：454-460.

[10]  顾娟，黄荣宗，刘振宇，等. 一种滑移区气体流动的格子Boltzmann曲边界处理新格式[J]. 物理学报，2017，66（11）：220-228.

[11]  程志林，宁正福，曾彦，等. 格子Boltzmann方法模拟多孔介质惯性流的边界条件改进[J]. 力学学报，2019，51（1）：124-134.

[12]  DE ROSIS A. Ground-induced lift enhancement in a tandem of symmetric flapping wings：Lattice Boltzmann-immersed boundary simulations[J]. Computers & Structures，2015，153：230-238.

[13]  SCHMIESCHEK S，SHAMARDIN L，FRIJTERS S，et al. LB3D：a parallel implementation of the Lattice-Boltzmann method for simulation of interacting amphiphilic fluids[J]. Computer Physics Communications，2017，217：149-161.

[14]  CHEN H D，CHEN S Y，MATTHAEUS W H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method[J]. Physical Review A，1992，45（8）：r5339.

[15]  LADD A J C，VERBERG R. Lattice-boltzmann simulations of particle-fluid suspensions[J]. Journal of Statistical Physics，2001，104（5/6）：1191-1251.

[16]  HE X Y，DOOLEN G. Lattice boltzmann method on curvilinear coordinates system：flow around a circular cylinder[J]. Journal of Computational Physics，1997，134（2）：306-315.