基于工程环境的气动多目标优化设计平台研究

李权， 郭兆电， 雷武涛， 赵轲

中航工业第一飞机设计研究院　总体气动研究所, 阎良　710089



基于工程环境的气动多目标优化设计平台研究

李权*， 郭兆电， 雷武涛， 赵轲

中航工业第一飞机设计研究院总体气动研究所, 阎良710089

摘要:工程环境中，飞机气动力设计面临在多个目标和多种约束条件下寻找最优值，需在较短时限内完成设计优化，并保证最终方案可靠。基于高性能计算环境，采用现代计算流体力学(CFD)数值模拟技术和优化技术等构建了面向实际工程的飞行器气动多目标优化设计平台：采用基于非均匀有理B样条(NURBS)方法的自由曲面变形技术，实现对工程复杂气动外形的参数化表达；采用网格变形技术，实现优化过程中计算网格的自动更新；采用基于有限体积方法和多块结构网格的雷诺平均Navier-Stokes(RANS)方程并行解算器进行气动力求解；采用基于精英保留策略的非支配排序的多目标遗传算法(NSGA-II)进行多目标全局优化求解；采用非线性单纯形算法进行局部优化求解,优化过程中，通过人工调整优化种群，引入人工经验，构建“人在回路”的设计流程。以某翼型/机翼气动力优化设计为例对该平台技术进行验证：多目标优化设计可得到清晰的Pareto前沿解分布；优化后的翼型/机翼在满足各项约束的前提下，具备更高的综合气动性能。结果表明：所发展的气动多目标优化设计平台具有很好的工程适用性。

关键词:多目标优化； 气动设计； 遗传算法； 计算流体力学； 自由曲面变形技术

现代飞机设计中，气动外形设计面临的要求、限制与矛盾越来越多，这对依赖工程经验“Cut and Try ”的试凑法和单点设计方法等传统设计方式提出了严峻的挑战。研究典型的气动多目标优化问题(如现代大型民机的机翼设计)时，需要在巡航、起降、爬升等多个设计点之间进行折衷，寻求综合最优解；但传统设计方法并不能很好地处理此类问题，多数情况下仅仅是找一个可满足各方约束条件的工程可行解，而非优化意义上的最优解。气动多目标优化设计就是根据飞机的各种性能要求，建立相应的目标函数和各种约束条件，对气动外形进行参数化处理，获得设计变量；然后采用现代数值优化方法，以定量分析的方式进行参数寻优，最终获得满足工程要求的综合最优解。多目标优化设计技术弥补了传统设计方法处理多学科、多目标、多约束设计问题的不足，因此更具工程应用价值，将是未来先进飞行器设计的必然选择[1-3]。

一个实用的气动优化设计平台需要解决以下技术问题：

1) 参数化建模技术优秀的外形参数化方法要求：控制参数尽量少，而所表达的外形的几何精度尽量高，设计范围足够大。目前比较流行的参数化建模技术主要有基于类函数/型函数(CST)的成形技术、非均匀有理B样条(NURBS)曲线/曲面技术和基于CATIA环境的参数化技术。需要重点发展控制参数少，成形精度高、范围广，执行效率高的参数化建模技术[4-7]。

2) 网格更新技术网格更新是优化迭代中气动力计算的前提。目前主要有网格重生成技术、基于商业软件执行脚本的网格更新技术和网格变形技术。各种网格技术都有一定的局限性，需根据具体问题灵活选用，提高网格更新的效率和质量。

3) 气动力预测技术气动力预测是气动优化设计的基础，工程化设计要求气动预测技术具备可靠的精度和较高的效率。

4) 优化搜索技术优化算法的实质是设计空间的搜素策略。根据气动多目标优化设计工作的特点，需重点发展针对多变量(100个以上)、多目标(10个以上)、多约束(100个以上)问题，全局性好，运行效率高的优化算法[8-10]。

工程环境中，飞机气动力设计不仅要找多目标和多约束条件下寻求最优解，还需要在较短的时间内完成设计优化，并最终保证方案可靠。但由于工程问题的复杂性、数值技术的不成熟等条件限制，依赖于计算机自动优化的设计技术在应用中还面临着很多矛盾，包括计算效率与计算精度、人工经验与自动优化、部件设计与整体设计、全局优化与局部寻优等[11]。特别是，为保证优化方案的可用性，在自动优化过程中，人工经验的引入必不可少。以往的一个误区认为，借助于计算机优化可以让无经验的设计师设计出很好的方案，这一想法实际很难达到，当前数值技术的成熟度还远不能支持依靠机器优化直接产生飞机方案。因此，实用性优化设计平台，必须处理好自动优化和人工经验之间的协调性。

本文将现代数值优化、计算流体力学(CFD)、高性能计算以及计算机辅助设计(CAD)等技术有机结合，依赖高性能计算集群的大规模并行计算，并结合专家知识与人工经验，构建面向工程实际的气动多目标优化设计平台。

1参数化建模技术

1.1翼型参数化

常用的翼型参数化方法有解析函数线性叠加法、多项式函数法和样条拟合方法等。2008年，美国波音公司的Kulfan和Bussoletti提出了一种基于CST的参数化方法[12-13]，该方法参数具有明确的几何意义，控制参数少，适应性强，精度较好。Kulfan等提出的CST方法对翼型进行参数化的表达式如下。

翼型上、下表面分别为

(1)

(2)

式中：yu和yl分别为翼型上、下表面纵坐标；yTEu和yTEl分别为翼型上、下表面后缘的纵坐标。

类函数C(x)定义为

(3)

型函数Su(x)和Sl(x)定义为

(4)

(5)

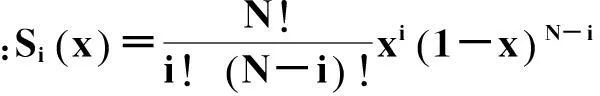
由上述分析可知，只要确定系数Aui和Ali，就可以确定整个翼型。可采用最小二乘法求解得到这些参数。

1.2基于NURBS的自由曲面变形技术

NURBS曲线/曲面方法在CAD/CAM 和计算机图形学等工程研究领域中得到了广泛应用。NURBS 方法的主要优点包括：基函数完备且正交、局域性好、曲面操作简单、网格梯度连续等。

假设一个NURBS曲面u方向为p阶，控制点数目为n+1；v方向为q阶，控制点数目为m+1；则三维曲面可表示为

(7)

Pi,j为控制点矢量，总数目为(n+1)×(m+1)；wi,j为权值系数；Ni,p(u)和Nj,q(v)分别为定义在非减点矢量U、V上的基函数,其表达式为

(8)

Ni+1,p-1(u)

(9)

(10)

Nj+1,q-1(v)

(11)

U(u)=

(r=n+p+1)

(12)

(s=m+q+1)

(13)

式中:v, vj, u, ui为节点值,用户可根据节点数列的基本要求进行灵活定义。由式(7)可知NURBS曲面实际上由(n+1)×(m+1)网格点阵控制，曲面的自由变形可通过移动这些控制点完成。

传统的采用直接移动控制点的方式进行曲面自由变形的方法，需要预先反算得到原曲面的控制点阵，反算过程的计算过大，因此不适合用于工程优化设计。本文采用在曲面上布置控制点阵，然后通过NURBS曲面描述新型面相对初始形面的变化量ΔS(u′,v′)，并将该变化量叠加到初始型面上获得新的外形，即

Snew=Sinitial+ΔS(u′,v′)

(14)

2网格更新技术

几何表面网格通过基于NURBS方法的自由曲面变形技术实现更新，表面网格变化产生的位移可采用线性插值方法光滑传递给空间网格。

(15)

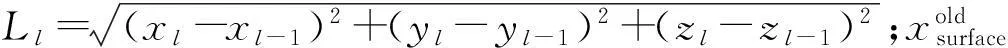
3气动力预测技术

文中气动设计平台的气动力预测模块主要包括：基于全速势方程的快速气动力预测方法、基于欧拉方程的气动力计算方法和基于雷诺平均Navier-Stokes(RANS)方程的精细气动力预测方法。随着高性能计算集群的大规模计算技术的高速发展，基于RANS方程的精细气动力求解技术已经在工程中得到了广泛应用。

3.1快速气动力预测方法

快速气动力预测采用基于守恒型全速势方程的数值积分进行无黏外流的计算，考虑了流动在激波位置非等熵突跃的特性；机翼三维层流或紊流附面层的计算采用有限差分法进行正计算或逆计算；分离流的计算采用涡黏性的Cebeci-Smith双层模型；黏性尾迹的计算采用近似方法，应用了Green二维积分公式。采用代数方法生成三维近似正交的C-H型计算网格。经验证，该计算程序对亚声速机翼气动特性，具有较好的预测精度。

3.2精细气动力预测方法

精细气动力预测采用三维RANS方程求解程序以及CCFD-MB软件。该程序基于有限体积法和多块结构网格求解RANS方程，湍流模型包括Spatart-Allmaras (SA)一方程模型和Menter-SST两方程模型。

三维积分形式的RANS方程为

(16)

式中：V为控制体体积；S为控制体表面面积；Q为守恒量;f为通过表面S的无黏通量和黏性通量之和;n为控制体表面S的外法向单位矢量。以有限体积法构造空间半离散格式，无黏通量项采用二阶Roe迎风通量差分格式离散，黏性通量项采用中心差分格式离散，隐式时间推进，采用多重网格技术加速收敛。该程序可通过关闭方程黏性项，退化为基于结构网格的三维欧拉方程求解器。该程序采用消息传递接口(MPI)并行方式，具有大规模并行计算能力，经测试可完成千核规模并行计算。

4优化算法

气动设计时经常需要同时处理多个目标问题。与单目标优化问题不同，多目标优化问题的解并不是唯一的，而是存在一个Pareto最优解集。Pareto最优解集就是不存在比这个解方案中至少一个目标更好而其他目标不低劣的更优解，其中任一目标的改进，必然引起其他至少一个目标的低劣。对于多目标优化问题，设计人员希望得到Pareto最优解集，然后根据最优解分布和人工经验进行多目标决策[14]。

遗传算法(GA)借鉴生物进化的思想，通过计算机模拟物种繁衍父代遗传基因的重新组合与“优胜劣汰”自然选择机制的联合作用，解决科学与工程中的复杂问题。遗传算法基于种群的操作机制，非常利于处理多目标优化问题的Pareto解集，已经有很多成功的应用[15]。目前，全球已经发展了很多针对多目标优化问题的遗传算法，如NSGA-II(Non-dominatedSortingGeneticAlgorithmII)[16]算法。NSGA-II算法根据产生的各种非劣前沿，采用了一种快速的非支配排序方法，从而减少了算法运行的整体时间。NSGA-II还使用了排挤算法来代替共享函数算法，使其无须确定一个共享参数就能控制个体的分布；引入了精英保留策略，提高种群的整体进化水平。在约束处理面，NSGA-II算法加入了一种高效的约束处理机制，不采用任何罚函数方法，而是通过引入一种虚拟的越界值，为所有的等式或不等式约束条件提供了一种通用解决方案。由于NSGA-II算法操作简单，具有全局搜索能力，而且有较好的收敛速度，其已成为多目标优化领域的基准算法之一。

除求解Pareto解集外，多目标优化的另一种方法是将多个目标加权整合为单个目标，采用高效率单目标优化方法进行综合寻优。但如何综合目标需要一定的工程经验。单目标寻优可采用效率优、鲁棒性好的直接搜索算法。

非线性单纯形算法是求解无约束非线性优化问题的优秀算法之一。它是一种直接搜索方法，不需要求解变量梯度，比基于梯度的优化算法更具适应性；它也是一种有效的局部搜索方法，迭代次数少，收敛速度快，对局部寻优计算，优于遗传算法等智能算法。

非线性单纯形法的基本原理：对于非线性模型中的n个代估参数，单纯形法按规则取n+1组近似值，构成初始单纯形；用此n+1组近似值计算n+1个目标函数并比较其大小，找出最大的目标函数值，并剔出相应的那组参数近似值；然后按一定的规则(反射、压缩、延伸等方法)换入新的1组参数近似值，用这组新的近似值与其他的n组近似值构成新的单纯形；如此反复计算、比较、剔除，直到最小的目标函数值以给定的精度逼近其极小值为止。对于有约束优化问题，一般通过给违反约束项施加惩罚函数进行处理。

5气动优化设计平台

本文的气动优化设计工作采用modeFRONTIER软件作为系统平台，集成前文所述的参数化模块、网格更新模块、气动力分析模块和优化算法模块等，构建灵活的设计体系，允许工程师协调效率与精度、人工经验与自动优化、部件设计与整体设计、全局优化与局部优化等的矛盾。

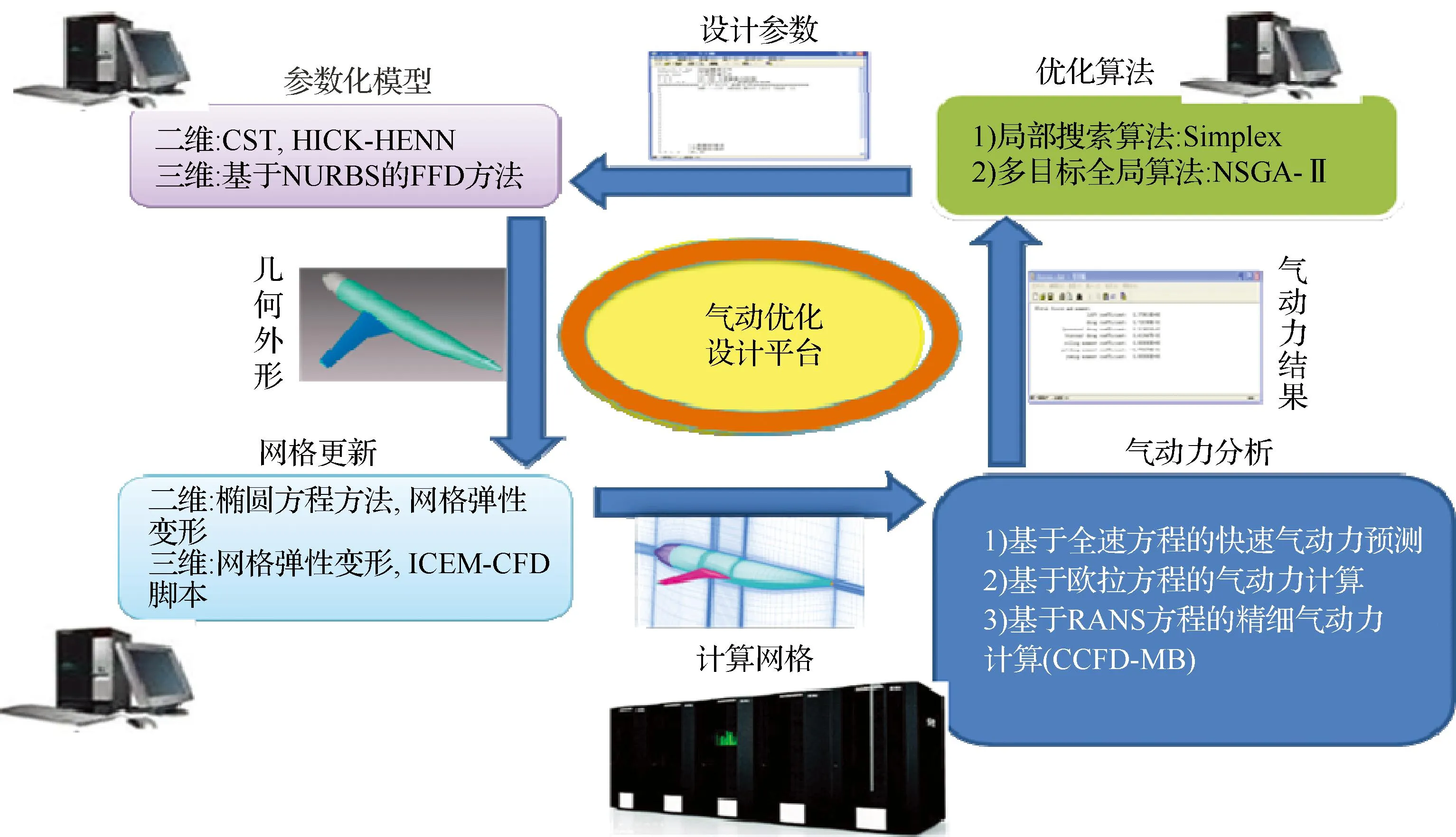
图1气动优化设计平台示意图
Fig. 1Frame of aerodynamic optimization design platform

图1为基本的气动优化设计平台。工程应用时，可以根据实际任务阶段和任务属性的不同，选择适当的方法构建相应的优化设计流程。如初步设计中，可采用遗传算法和速势方程等快速气动力分析技术，进行全局性、高效率的初步优化设计；详细设计中，则采用局部优化算法和基于RANS方程的气动力求解技术，进行精细气动力设计。这些措施有助于协调优化设计中效率与精度、全局优化与局部优化之间的矛盾。

为提高优化效率和保证优化方案的可用性，自动优化过程中，人工经验的引入必不可少。气动优化设计流程中，可通过3个途径引入人工经验。

1) 初始种群时，将优秀基因放入优化种群。如工程单位通常建立了翼型库，积累了大量经过验证的优秀翼型，新翼型优化时，可根据指标从翼型库中挑选一些较好的翼型，将其参数化后，加入到优化种群中参与寻优。

2) 构建“人在回路”的优化流程。优化过程中，根据人工经验，灵活调整优化种群，改善优化进度或进行定向优化。例如，对多目标优化问题，初步优化时缺乏经验，目标数量设置较多，当优化到一定程度后，可根据人工经验，将某些已达标目标解加入到优化种群中，同时将该目标调整为约束，重新优化只集中针对关心目标，这可有效提高优化效率。

3) 根据人工经验制定适当的约束条件与目标规划，保证优化结果的工程可用性。设计约束包括几何约束和气动力约束。几何约束包括：翼型最大厚度、机翼容积、机翼前/后梁厚度、几何表面曲率要求等；气动力约束包括：机翼低头力矩、机翼抖振边界、失速特性等。几何约束通过编写几何测量程序自动计算得到。部分气动力约束可通过CFD直接计算得到，但失速特性和分离形态(如机翼前缘约束，展向扭转约束等)却不能通过直接计算准确得到，而需要根据人工经验间接处理。

采用基于NURBS方法的自由曲面变形技术和网格自动更新技术，可保证在整体外形的框架下进行部件优化，兼顾部件与整体之间的耦合干扰。优化过程中网格拓扑和整体网格都不变，仅局部根据几何变形而变形，优化结果之间由于网格变化导致的误差较小，确保精细化设计要求。

常规计算机求解三维RANS方程，计算规模小、时间长，不能满足优化效率要求。为提高优化的时效性，需基于高性能计算机开展大规模并行计算及优化。为实现优化过程中对作业任务的自动管理和维护，需采用一定的作业调度系统。作业调度系统采用开源的Open-PBS系统，并通过PBS提供的脚步命令，编写了作业调度和监控程序，保证在优化过程中，按需自动分配计算资源。

6设计实例

6.1翼型双目标优化

1) 设计状态[17]

工况 1: 马赫数Ma= 0.65, 升力系数CL= 1.0, 雷诺数Re= 5.0×106。

工况 2:Ma=0.80,CL=0.8,Re=5.0×106。

2) 优化目标: 各工况阻力最小

3) 约束条件

a) 翼型面积和最大厚度不减；

b) 前缘半径不减小；

c) 低头力矩系数小于0.1。

4) 参数化与网格

采用8阶CST方法对翼型进行参数化，设计变量共计17个。计算网格采用求解椭圆型方程生成C型结构网格，网格规模为345×101(见图2)。网格更新通过网格生成程序，按照新的翼型坐标点重新生成。气动力求解器采用CCFD-MB，湍流模型选择SA模型。

图2翼型的C型结构网格
Fig. 2“C” type structured grid of airfoil

5) 设计流程

图3为采用modeFRONTIER构建的翼型双目标优化设计流程。采用NSGA-II算法进行多目标优化求解，随机产生35个初始种群，进化代数为40代。其中:CL_1，CL_2分别为工况1、工况2的升力系数；CD_1，CD_2为阻力系数；Cm_1，Cm_2为力矩系数。

6) 优化结果

图4给出了优化后所有解在设计目标平面上的分布，其中深色实心点为可行解(Feasible)，浅色虚心点为不满足约束的不可行解(Unfeasible)。图5为滤除不可行解后的可行解分布，可以看到清晰的Pareto前沿分布。图6为最优的选取图，并标出了RAE2822翼型的原始解。期望的典型优化解包括A、B、C 3个:A翼型在工况2阻力略小于原始翼型的前提下，工况1阻力最小；C翼型在工况1阻力略小于原始翼型的前提下，工况2阻力最小；B翼型为A翼型与C翼型的折中。图7为A、B、C翼型同RAE2822原始翼型的几何对比，B的几何外形刚好处在A与C之间。图8和图9为2种工况下各翼型的压力分布对比，图中,Cp为压力系数。

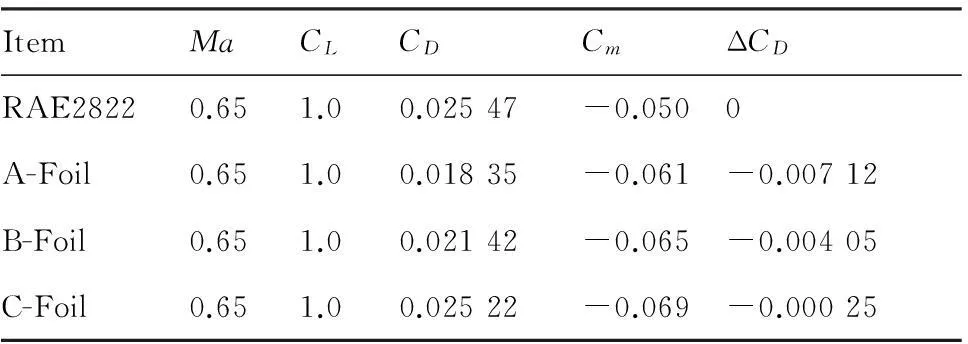
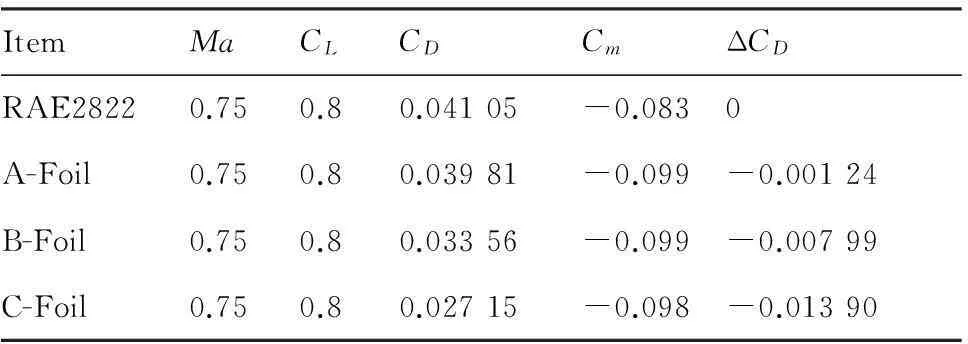
表1和表2分别给出了2种工况下各翼型的气动力结果，可以看到相对于原始翼型，优化翼型在满足各种约束的前提下，性能有了明显提升。折中方案B翼型在2个设计点上综合性能较优，相对于原翼型，工况1和工况2的计算阻力分别降低了约40 counts和80 counts。

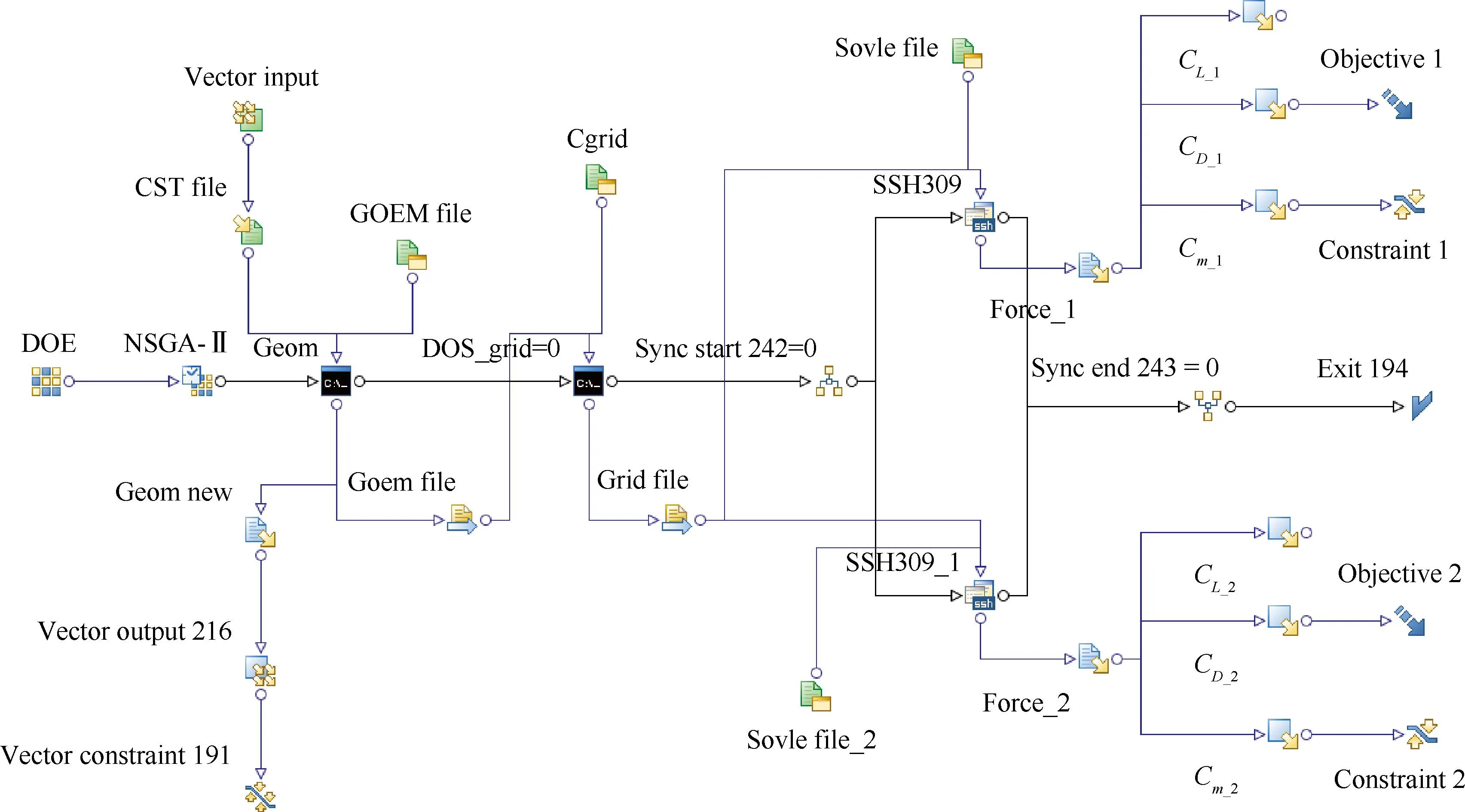
图3翼型双目标优化流程
Fig. 3Optimization flowchart of airfoil bi-objective design

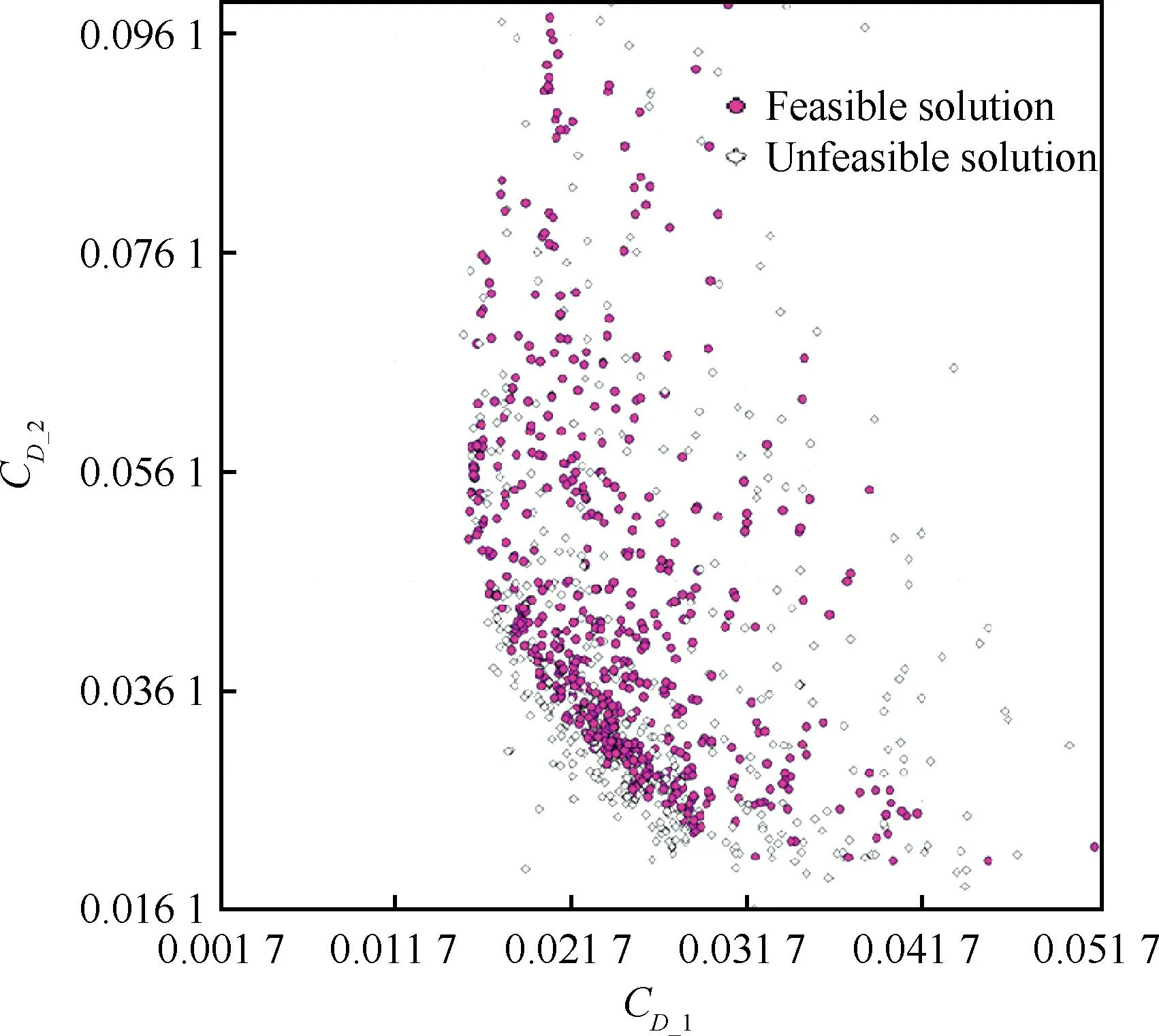
图4可行解与不可行解分布
Fig. 4Distribution of feasible solution and non-feasible solution

图5Pareto前沿解分布
Fig. 5Distribution of Pareto frontier solution

图6最优解选取图
Fig. 6Selection of optimization solution

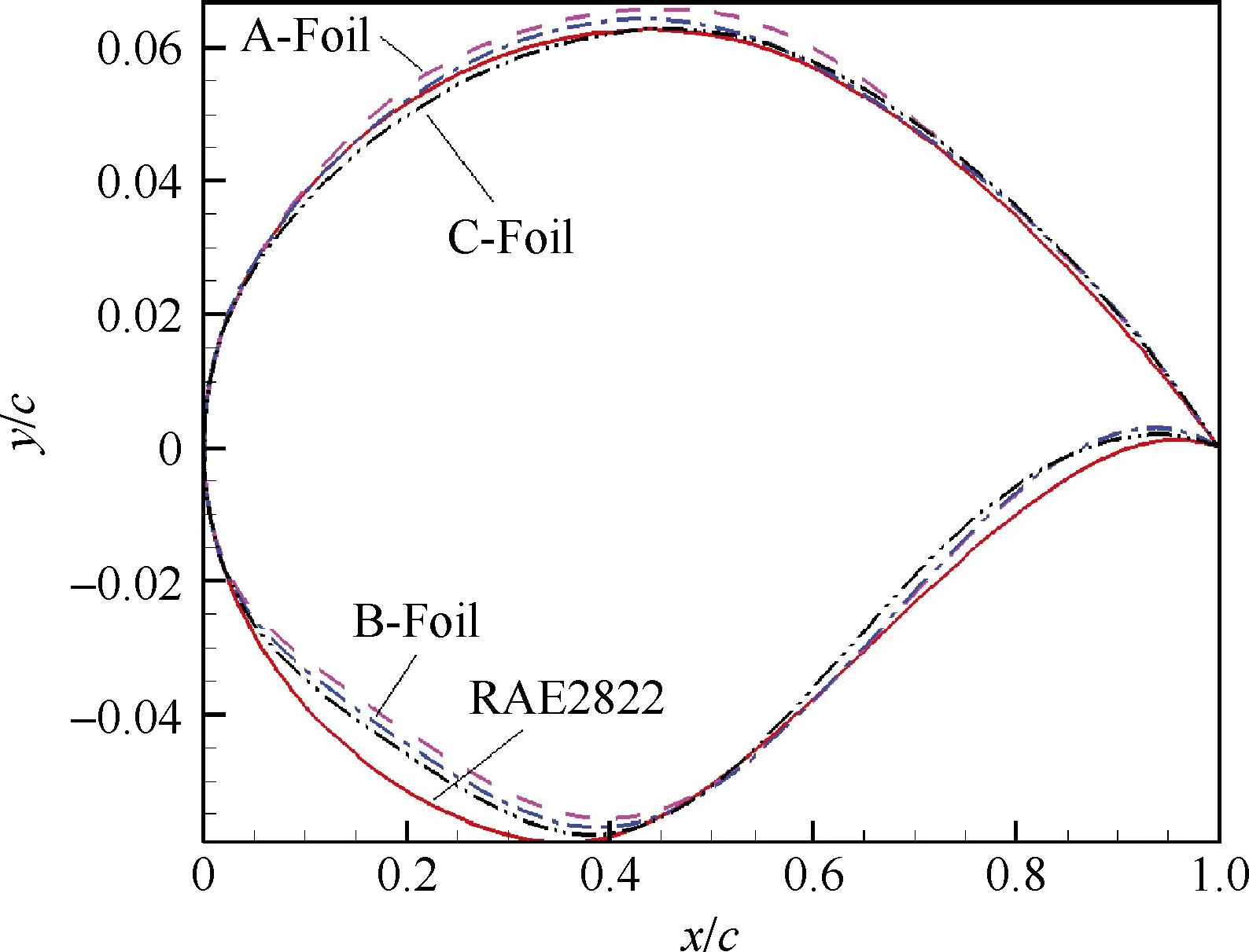
图7翼型几何对比
Fig. 7Comparison of airfoils’ geometry

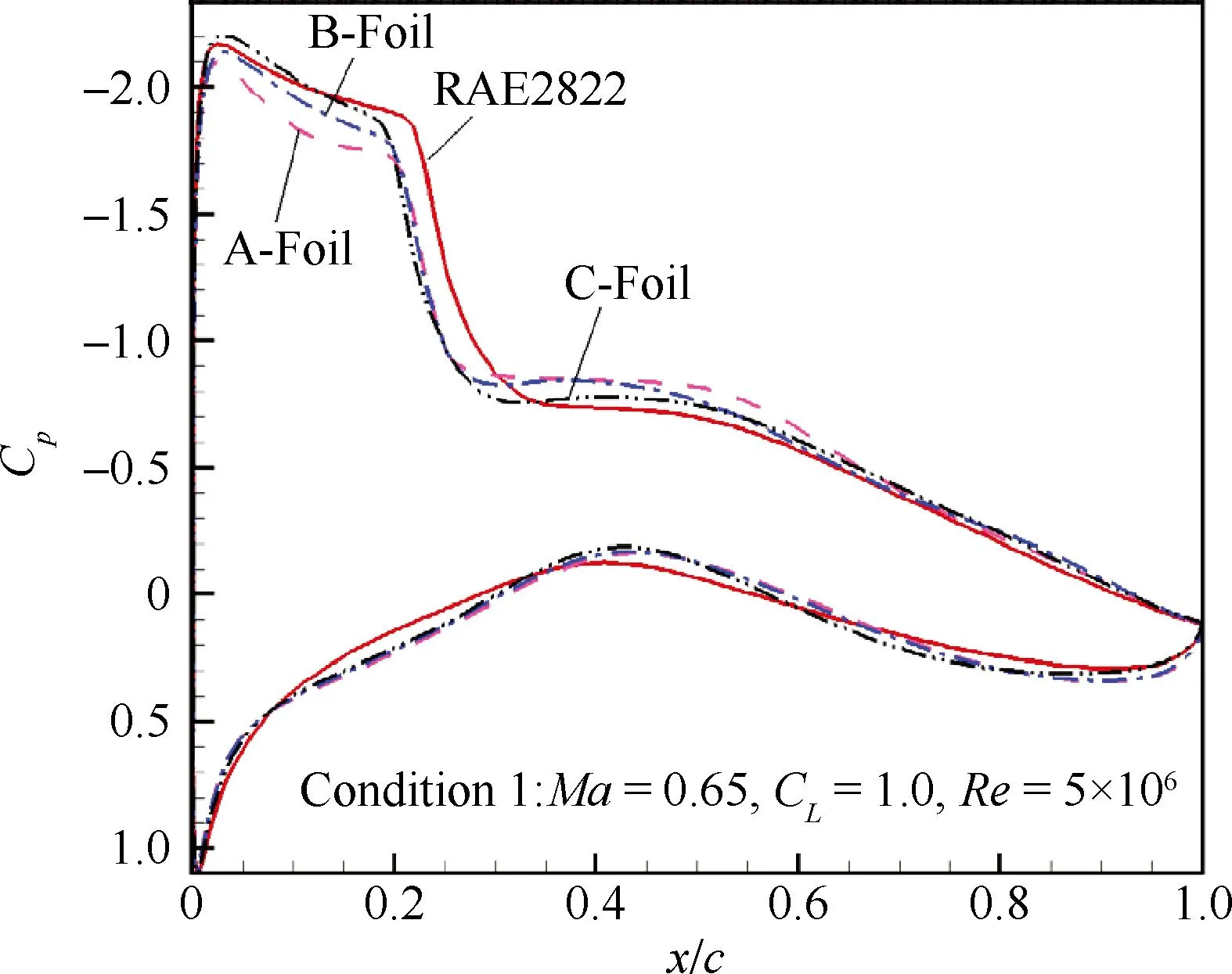
图8工况1下各解的压力分布
Fig. 8Pressure coefficient distribution of solution (condition 1)

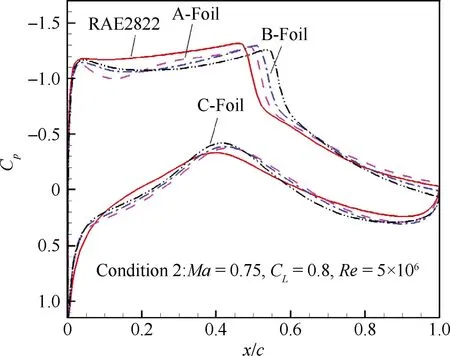
图9工况2下各解的压力分布
Fig. 9Pressure coefficient distribution of solution (condition 2)

表1工况1下的气动力结果对比

Table 1Comparison of aerodynamic results under Condition 1

ItemMaCLCDCmΔCDRAE28220.651.00.02547-0.0500A-Foil0.651.00.01835-0.061-0.00712B-Foil0.651.00.02142-0.065-0.00405C-Foil0.651.00.02522-0.069-0.00025

表2工况2下的气动力结果对比

Table 2Comparison of aerodynamic results under Condition 2

ItemMaCLCDCmΔCDRAE28220.750.80.04105-0.0830A-Foil0.750.80.03981-0.099-0.00124B-Foil0.750.80.03356-0.099-0.00799C-Foil0.750.80.02715-0.098-0.01390

6.2M6机翼阻力优化

1) 设计状态[18-19]Ma= 0.84，Re=1.17×107，迎角α=3.06°。

2) 优化目标阻力最小。

3) 约束条件

a) 升力系数变化小于0.01；

b) 机翼最大厚度不减小，0.15弦长和0.80弦长处厚度不减小。

4) 机翼参数化

沿机翼展向，每间隔25%展长确定一个优化剖面，共选择5个剖面(见图10)。每个剖面按图11所示的方式布置控制点，上下表面各8个，共计16个。上下表面的第1个和最后1个控制点(图11中的a0、a7、b0、b7)保持固定。上表面的实际可动控制点为a1、a2、a3、a4、a5、a6；下表面可动控制点为b1、b2、b3、b4、b5、b6。其中，a1和b1点控制翼剖面前缘半径，可沿上下、前后2个自由度运动，其他控制点只允许沿上下方向运动，这样，单剖面的控制变量数共计14个。全机翼变形的控制变量数共计70个。

图10机翼表面控制点分布
Fig. 10Distribution of control points on wing surface

图11机翼剖面控制点分布
Fig. 11Distribution of control points of wing section

5) 网格更新

初始网格采用ICEM-CFD软件生成的多块结构网格，共计32块，113万网格单元。移动机翼表面的控制点，采用前文基于NURBS的曲面变形技术产生机翼表面变形(如图12所示)，然后采用网格变形算法，将表面变形光滑传递给空间网格(如图13所示)，实现计算网格更新。

图12机翼表面变形示意图
Fig. 12Deformation of wing surface

图13空间网格变形示意图
Fig. 13Deformation of space grid

6) 气动力计算

采用CCFD-MB程序，湍流模型选择SA模型，通过modeFRONTIER软件的SSH(Secure Shell)节点连接到远程高性能集群上，采用基于PBS(Portable Batch System)系统的队列程序自动分配计算资源。

7) 设计流程

采用GA+Simplex混合方法进行优化，遗传算法初始种群35个，其中25个采用带约束的随机算法产生，其他10个根据人工经验添加。先采用遗传算法进行全局寻优， 30代后，进化已非常缓慢；终止优化，从现有的优化解选择70个优解，组成新的初始种群，采用非线性单纯形算法进行二次局部寻优。图14为机翼阻力收敛历程，其中CD obj为阻力系数的优化目标。

图14机翼阻力收敛历程
Fig. 14Convergence of wing drag coefficient

8) 结果分析

表3给出了优化机翼与原机翼的气动力对比，其中CDp和CDf分别为压差阻力和摩擦阻力。优化机翼总阻力减小约32 counts,其中压差阻力占26 counts。图15为优化机翼与原机翼压力云图对比，图中显示原机翼(M6)上表面有明显的“λ”形激波，而优化机翼(Opt)上表面该波形已基本消失。

表3　M6机翼气动力结果对比

图15优化机翼与原机翼压力云图对比
Fig. 15Comparison of pressure contour between optimized wing and initial wing

在2幅机翼上分别取6个剖面，图16为机翼刻面站位示意图。图17给出了各剖面压力分布对比，可见优化机翼各剖面上的吸力峰值明显降低，激波强度也减弱，但翼梢激波未消除。图18给出的几何对比表明，优化机翼的各剖面厚度完全满足约束要求。

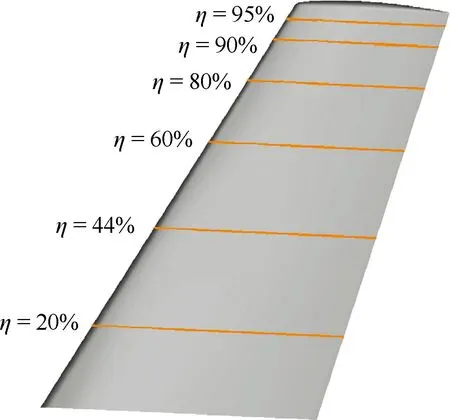
图16机翼剖面站位示意图
Fig. 16Stations of wing section

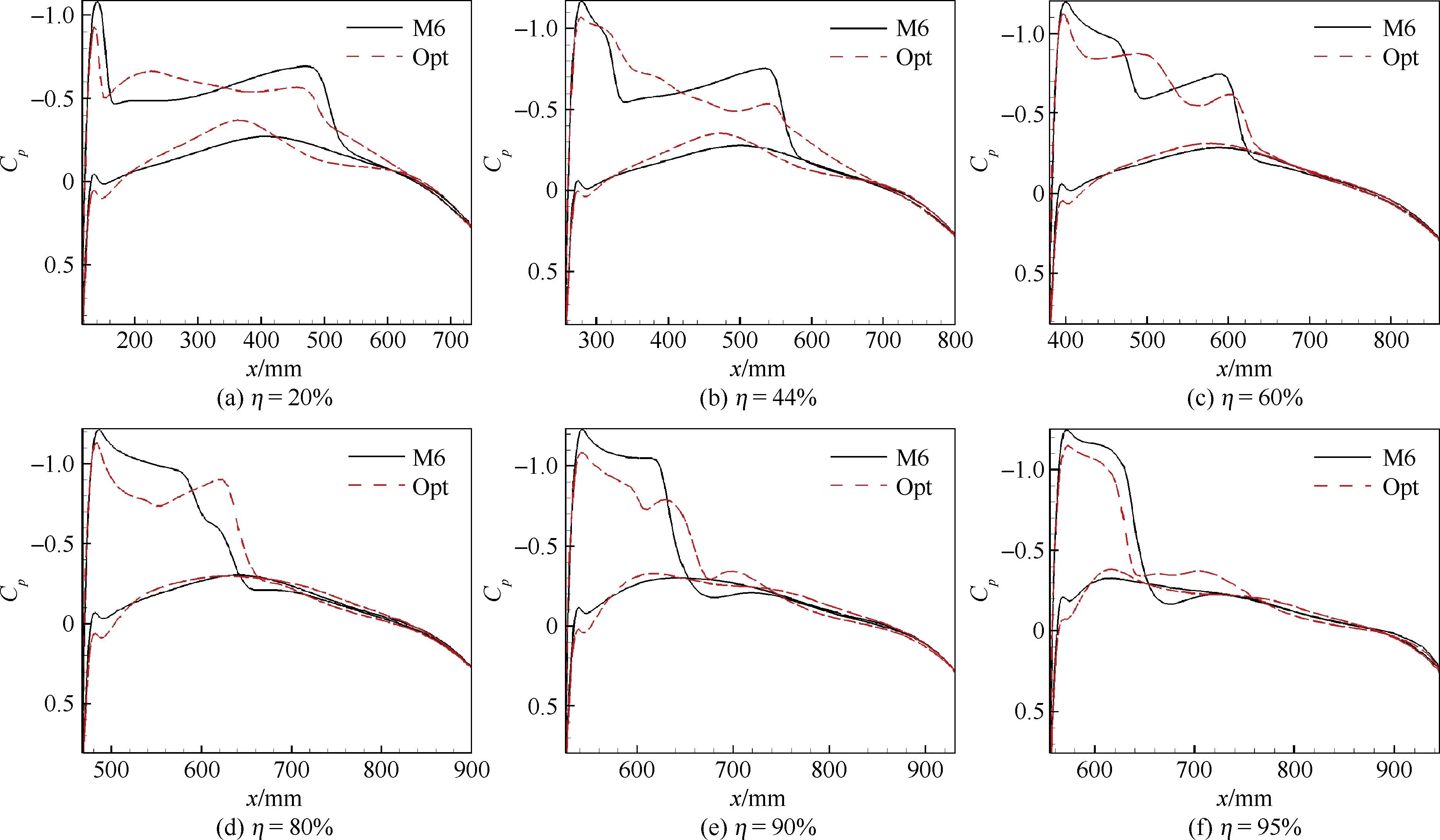
图17机翼各剖面压力分布对比
Fig. 17Comparison of pressure coefficient of wing sections

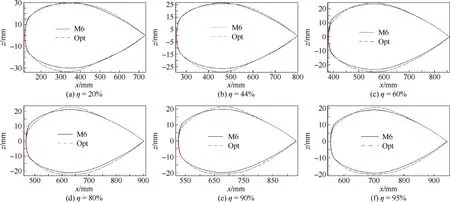
图18机翼各剖面几何对比
Fig. 18Comparison of geometry of wing sections

6.3民机机翼多点优化设计

1) 基本构型: 民机翼身组合体。

2) 设计工况[20]

工况1：CL=0.525,Ma=0.74,Re=3.0×106。

工况 2：CL=0.525,Ma=0.78,Re=3.0×106。

工况 3：CL=0.525,Ma=0.80,Re=3.0×106。

3) 优化目标固定升力，各工况阻力最小。

4) 约束

a) 翼型最大厚度不减小；

b) 翼型15%、65%弦长处厚度不减小；

c) 升力系数不减小;

d) 低头力矩不增加。

5) 机翼参数化

机翼参数包括5个控制剖面参数及其扭转角。图19给出了机翼平面形状和控制剖面(Root、Z2、Z3、Z4、Tip)。翼型参数化采用8阶CST方法，单个翼型上下表面各9个参数(后缘厚度固定)。优化参数共计：5×9×2+5=95个。

6) 优化流程

优化流程如图20所示，采用NSGA-II算法进行多点多目标优化设计;采用基于速势方程的快速计算法进行气动特性评估。

图19机翼平面形状及控制剖面
Fig. 19Wing plane and control section

7) 结果分析

本次优化工况集中在高马赫数，设计期望减小工况2阻力，保证其他工况的协调性。根据这一设计期望，作者从优化的Pareto解集中挑选合适的优化机翼。表4给出了优化机翼与原始机翼的气动力计算结果(其中，CD_INIT和CD_OPT分别表示原始和优化机翼的阻力系数结果，CL/CD_INIT和CL/CD_OPT分别表示原始和优化机翼的升阻比结果，Cm_INIT和Cm_OPT分别表示原始和优化机翼的力矩系数结果)，相对于原始机翼，在满足各种约束的情况下，优化机翼减阻效果显著，其中工况2的升阻比提高约4.1%。图21和图22分别为工况3下计算的优化机翼与原始机翼的压力云图和典型剖面的压力分布对比，其中INIT代表原始机翼，OPT代表优化机翼,可以看到优化机翼的激波强度显著下降。

表4　气动力结果对比

图20优化设计流程
Fig. 20Optimization design flowchart

图21机翼压力分布对比
Fig. 21Comparison of pressure contours between initial wing and optimized wing

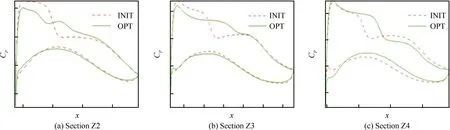
图22机翼典型剖面压力分布对比
Fig. 22Comparison of pressure coefficients of typical wing sections

7结论

气动优化设计是飞机研制中至关重要的环节之一。本文分析了气动自动优化设计中的难点与矛盾，针对工程实际要求，采用先进CFD技术和数值优化技术等构建了气动多目标优化设计平台,通过3个气动设计算例，可得到如下结论。

1) 工程环境中对气动设计提出来更多的设计要求和约束，传统的气动优化设计方法和系统不能很好地处理工程设计实际问题。

2) 通过构建“人在回路”的设计流程，引入人工经验，保证优化方案面向工程实际。一方面提高了设计效率，另一方面使得优化结构满足工程需求。

3) 通过翼型、三维机翼的气动优化设计，对平台技术进行了验证，多目标优化设计可得到清晰的Pareto前沿解分布；优化后的翼型/机翼在满足各项约束的前提下，具有更高的综合气动性能。结果表明：本文发展的气动多目标优化设计平台具有很好的工程适用性。

参考文献

[1]高正红. 气动外形优化设计方法研究与存在问题[C]//大型飞机关键技术高层论坛暨中国航空学会2007年学术年会. 北京： 中国航空学会， 2007： 1-5.

GAO Z H. The research progress in aerodynamic shape optimization methods[C]//2007 Academic Annual Meeting of the China Aviation Society. Beijing: China Aviation Society, 2007: 1-5 (in Chinese).

[2]余雄庆. 飞机总体多学科设计优化的现状与发展方向[J]. 南京航空航天大学学报， 2008, 40(4): 417-426.

YU X Q. Multidisciplinary design optimization for aircraft conceptual and preliminary design: Status and directions[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 417-426 (in Chinese).

[3]JAMESON A. Computational fluid dynamics and airplane design: Its current and future impact[R]. Cincinnati: Lecture in University of Cincinnati, 2008: 6-8.

[4]JASON E H, DAVID W Z. Aerodynamic optimization algorithm with integrated geometry parameterization and mesh movement[J]. AIAA Journal, 2010, 48(2): 400-413.

[5]MOUSAVI A, CASTONGUAY P, NADARAJAH S K. Survey of shape parameterization techniques and its effect on three-dimensional aerodynamic shape optimization[C]//Proceeding of the 18th AIAA Computational Fluid Dynamics Conference. Reston: AIAA, 2007: 25-28.

[6]SAMAREH J A. Aerodynamic shape optimization based on free-form deformation: AIAA-2004-4630[R] . Reston: AIAA, 2004．

[7]陈波, 高学林, 袁新. 基于NURBS 的叶片全三维气动优化设计[J]. 工程热物理学报, 2006, 27(5): 763-765.

CHEN B, GAO X L,YUAN X. Three-dimensional blade aerodynamic optimization design based on NURBS[J]. Journal of Engineering Therophysics, 2006, 27(5): 763-765 (in Chinese).

[8]KOCH P N, SIMPSON T W, ALLEN J K, et al. Statistical approximations for multidisciplinary design optimization: the problem of size[J]. Journal of Aircraft. 1999, 36(1): 275-286

[9]李董辉， 童小娇， 万中． 数值最优化[M]． 北京: 科学出版社, 2005: 45-47.

LI D H, TONG X J, WAN Z. Numerical optimization[M]. Beijing: Science Press, 2005: 45-47 (in Chinese).

[10]VANDERPLAATS G. Very large scale optimization: NASA/CR-2002-211768[R]. Washington, D.C.: NASA,2002.

[11]张宇飞. 基于先进CFD方法的民用客机气动优化设计[D]. 北京： 清华大学， 2010: 13-16.

ZHANG Y F. Aerodynamic optimization design of civil aircraft based on advanced CFD method [D]. Beijing: Tsinghua University, 2010: 13-16 (in Chinese).

[12]KULFAN B M. Universal parametric geometry represe- ntation method[J]. Journal of Aircraft， 2008, 45(1): 142-158.

[13]KULFAN B M, BUSSOLETTI J E. Fundamental parametric geometry representations for aircraft component shapes: AIAA-2006-6948[R]. Reston: AIAA, 2006.

[14]PEIGIN S， 朱自强， EPSTEIN B. 可应用于民机空气动力设计中的数值优化方法[J]． 航空学报, 2014, 35(1): 58-69.

PEIGIN S, ZHU Z Q, EPSTEIN B. Applicable numerical optimization methods for aerodynamic design of civil aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 58-69 (in Chinese).

[15]崔逊学. 多目标进化算法及其应用[M]. 北京： 国防工业出版社， 2008: 13-14.

CUI X X. Multi-objective evolutionary algorithm and its application[M]. Beijing： National Defense Industry Press, 2008: 13-14 (in Chinese).

[16]DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 181-197.

[17]REUTHER J J, JAMESON A, ALONSO J J, et al. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, Part2[J]. Journal of Aircraft, 1999, 36(2): 61-74.

[18]EPSTEIN B, JAMESON A, PEIGIN S, et al. Comparative study of three-dimensional wing drag minimization by different optimization techniques: AIAA-2008-0326[R]. Reston: AIAA, 2008.

[19]王晓鹏. 遗传算法及其在气动优化设计中的应用研究[D]. 西安： 西北工业大学， 2000: 40-46

WANG X P. Genetic algorithm and its application in aerodynamic optimization design[D]. Xi’an: Northwestern Polytechnical University, 2000: 40-46 (in Chinese).

[20]王晓璐， 朱自强， 吴宗成， 等. 基于N-S方程的民航机翼双目标优化设计[J]. 北航航空航天大学学报， 2008, 34(7): 739-742.

WANG X L, ZHU Z Q, WU Z C, et al. Bi-objective optimization design of civil transport wing using N-S equations[J] . Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(7): 739-742 (in Chinese).

李权男， 博士研究生， 高级工程师。主要研究方向： 气动力设计与数值计算。

Tel: 029-86832360

E-mail: lqq0309@163.com

郭兆电男， 学士， 研究员。主要研究方向： 飞机设计。

Tel: 029-86832602

E-mail: guozd@163.com

雷武涛男， 硕士， 高级工程师。主要研究方向： 飞机设计。

Tel: 029-86832602

E-mail: lei_wu_tao@yahoo.com

赵轲男， 博士， 工程师。主要研究方向： 飞机气动力设计。

Tel: 029-86832602

E-mail: zhaokecfd@163.com

Received： 2015-09-30; Revised: 2015-11-17; Accepted: 2015-11-22; Published online: 2015-12-0410:08

URL： www.cnki.net/kcms/detail/11.1929.V.20151204.1008.008.html

Foundation item： National High-tech Research and Development Program of China (2012AA01A304)

Engineering environment-based multi-objective optimization platform for aerodynamic design

LI Quan*, GUO Zhaodian, LEI Wutao, ZHAO Ke

General Configuration and Aerodynamic Institute, The First Aircraft Institute of AVIC, Yanliang710089, China

Abstract:In the engineering environment, the aim of aerodynamic design of an aircraft is to find the optimal value under the multi-objectives and multi constraints. The design optimization should be completed in a short time and the final scheme must be reliable. Based on high-performance computing environment, an engineering-practical multi-objective optimization platform for aerodynamic design is constructed by adopting modern computational fluid dynamics (CFD) numerical simulation and optimization techniques. The free form deformation method based on non-uniform rational b-splines (NURBS) is used to obtain the parametrized representation of aerodynamic shapes; the mesh deformation method is taken to realize the automatic deformation of computational mash in optimization; a Reynolds averaged Navier-stokes solver based on finite volume method and multi-block structured mesh is used to find out aerodynamic forces; the non-dominated sorting-based multi-objective genetic algorithm (NSGA-II) is used to search for global optimum, while the nonlinear simplex algorithm method is used to search for local optimum. During the optimization process, a “human-in-the-loop” design process is configurated through artificially changing optimum population and introducing artificial experience. For the validation of this platform, optimization design of an airfoil/wing’s aerodynamic forces is taken as an example. A clear Pareto-optimal front can be obtained by multi-objective optimization design; on the premise of meeting all constraints, the comprehensive aerodynamic performance of optimized airfoil/wing is significantly improved. The result shows that the multi-objective optimization platform for aerodynamic design developed in this paper can be well applied to engineering practice.

Key words:multi-objective optimization; aerodynamic design; genetic algorithm; CFD; free form surface deformation technology

*Corresponding author. Tel.： 029-86832360E-mail: lqq0309@163.com

作者简介：

中图分类号：V211

文献标识码：A

文章编号：1000-6893(2016)01-0255-14

DOI：10.7527/S1000-6893.2015.0315

*通讯作者.Tel.： 029-86832360E-mail: lqq0309@163.com

基金项目：国家“863”计划(2012AA01A304)

收稿日期：2015-09-30； 退修日期： 2015-11-17； 录用日期： 2015-11-22； 网络出版时间： 2015-12-0410:08

网络出版地址： www.cnki.net/kcms/detail/11.1929.V.20151204.1008.008.html

引用格式： 李权， 郭兆电， 雷武涛， 等． 基于工程环境的气动多目标优化设计平台研究[J]. 航空学报， 2016, 37(1): 255-268. LI Q, GUO Z D, LEI W T, et al. Engineering environment-based multi-objective optimization platform for aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 255-268.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn