高超声速飞行器研制系统工程风险概率分析

沈作军， 柳青， 肖佳平

1. 北京航空航天大学 航空科学与工程学院， 北京　100083

2. 中国航天科工集团第三研究院， 北京　100074



高超声速飞行器研制系统工程风险概率分析

沈作军1, *， 柳青2， 肖佳平1

1. 北京航空航天大学 航空科学与工程学院， 北京100083

2. 中国航天科工集团第三研究院， 北京100074

摘要:针对高超声速飞行器研制工程的高风险特点，对工程决策方和研制方面临的不同类型风险进行了建模分析。基于系统方案或关键技术的固有风险概率和抽象化的研发与验证过程，分别计算分析了工程决策方误判验收通过不合格产品和研制方过度研发或重复验证较低失败概率产品的风险概率，进而提出了高风险研发项目中研制方过度研发风险的概念，明确了工程决策误判风险与研制方过度研发风险的相互影响规律，并基于概率方法建立了一种可以综合权衡决策方风险和研制方风险、合理确定研制周期的系统工程优化方法。

关键词:高超声速飞行器； 研制工程； 过度研发风险； 决策方风险； 风险概率； 系统工程优化

高超声速飞行器一般指能以5倍以上声速在稠密大气内持续巡航的飞行器。这类飞行器的研制难度大大超过传统飞行器。从半个世纪前美国X-15飞行器算起，主要航空航天国家在高超声速飞行器领域启动过大量的研发计划，但目前尚未成功研发出一款实用的高超声速飞行器。国内外实践表明，此类飞行器从基础理论、实验验证手段到飞行试验各个环节均存在较大的研制风险和较多的不确定因素。尤其过去十多年来，以美国X-43A和X-51为代表的吸气式高超声速飞行器，以及以HTV-2为代表的高超声速滑翔飞行器都在其飞行试验中经历了一系列失败[1]。根据美国工程审查委员会的调查结果，尽管失败的原因各不相同，但分析共性问题表明，现有的基于传统飞机和轨道航天器的飞行器设计准则及系统研发体系并不完全适用于临近空间高超声速飞行器[2]。正如美国NASA前局长针对日益增多的复杂系统研制失败或研制周期拖延的现状所表述的，对风险和复杂程度日益增加的飞行器系统研制，严格按传统系统工程过程做了每一件该做的事情，但依然不可避免研制失败或延误[3]。这意味着在航空航天复杂系统研发中屡试不爽的系统工程方法面临着新的挑战。

由于高超声速飞行器在航空航天领域和国防方面的重大意义，这类飞行器的研制往往以国家工程的形式进行，如美国的NASP计划等。高超声速飞行器因此受到更多的关注，研发计划或工程决策方对研制过程中的失败也更加敏感。这一特点往往导致传统型号研制中的风险控制办法被更加严格地应用于高超声速飞行器研发，“万无一失”的观念时常成为贯穿研发过程的主线。然而，高超声速飞行器鲜明的高风险和探索性特点，以及对研发资金投入和研制周期日益苛刻的约束，都要求我们必须从更全面的角度来审视研发过程是否具有更高的效率。

高超声速飞行器不同于传统飞行器的一个主要特点在于其研发过程中不可避免的高风险特点，而针对传统复杂系统研发的系统工程理论和方法更加适合应对具有确定设计结果的系统，通过研制阶段划分和系统工程过程控制[2]，在划定的阶段和环节完成了规定的工作事项就可得到预期的结果。在飞行器研制系统工程研究领域，相关成果大多具有定性的特点[4-7]，或针对特定技术系统进行风险分析[8-10]。风险分析方法在系统工程领域也得到了广泛的研究[11-15]，但这些研究大多围绕飞行器研制中的特定技术性风险，或围绕技术风险因素进行系统技术方案设计权衡分析[16-18]。

高超声速飞行器研制工程的风险不仅存在于基础理论和技术领域，而且也存在于对阶段性研发结果的判断和决策。另外，研发周期延误和费用超限也是决定工程前景的风险因素。因此，如何将技术风险和决策判断风险进行综合分析，并同时考虑研发周期因素，是系统工程领域值得深入研究的内容。这方面公开见诸文献的研究不多。针对这一目标，本文借鉴航天制导领域的蒙特卡罗随机仿真技术[19]，将随机过程中的概率计算方法[20]扩展应用到高风险系统研制中的决策性和技术性风险分析与权衡，并基于抽象化的研制性试验验证失败概率模型，在综合考虑各类风险因素的基础上实现对研制过程的动态优化。

1基于概率的决策方验收准则

假设某系统或某项待试验验证的技术尚未完全成熟，在实际条件下发生失效/失败的概率为p，根据伯努利公式，n次试验中发生k次失效/失败的概率为

(1)

(2)

式(2)亦可理解为，如果以n次试验中不超K次失效/失败为系统满足技术要求的接受标准(以下简称(n，K)标准)，则系统实际运行时发生失效/失败次数超出这一标准的可能性为1-Pn,K。因此，式(2)代表了实际系统满足技术要求的置信度(以下由q表示)。型号研制工程中，这一基于概率的接受标准被广泛应用于项目决策方判断系统研制是否满足相关技术指标要求。

表1为系统固有失败概率为5%、置信度为90%的(n，K)标准示例。

表1　(n，K)标准示例(p=5%，q=90%)

由于90%置信度的要求，表1显示的可接受失败次数显著低于概率p与试验总次数n的乘积。图1给出了n=133、p=5%时不同失败次数的发生概率。

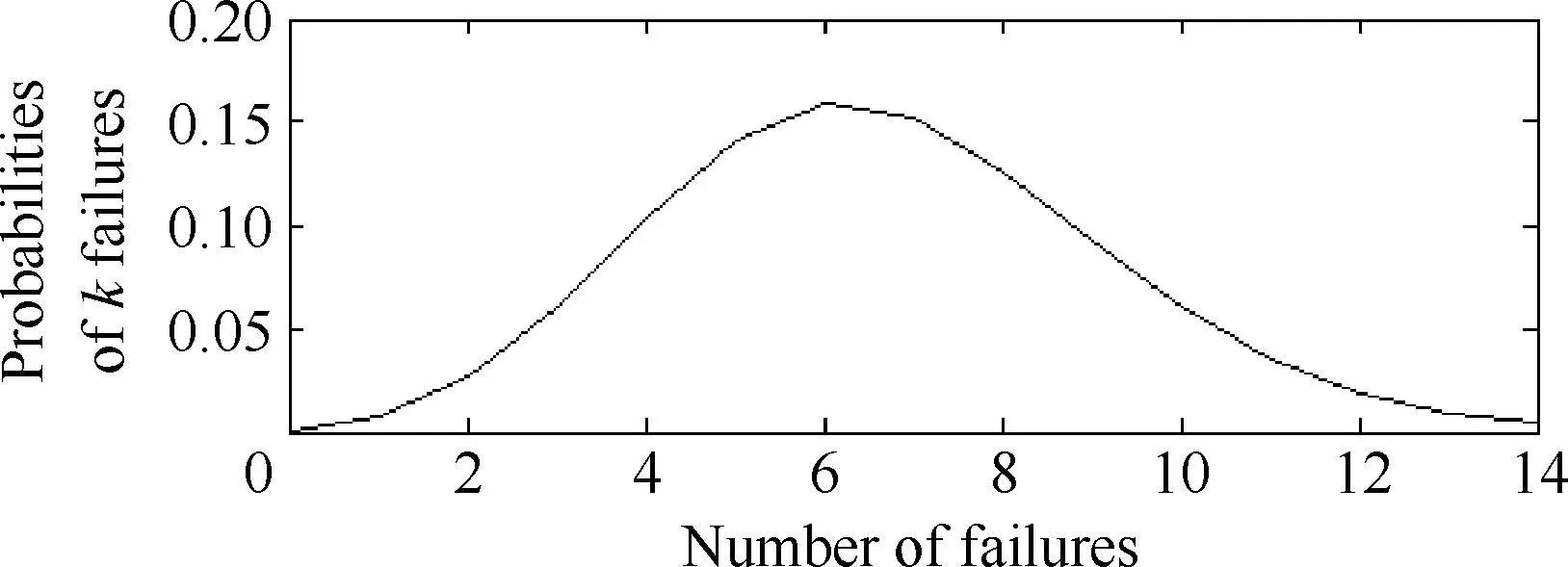
图1失效/失败次数及其发生概率(n=133，p=5%)
Fig. 1Number of failures and corresponding probabilities(n=133，p=5%)

表1所示的样本总数n与可接受失败次数上限K通常成为系统研发结果的验收准则。图2为针对系统设计指标p=5%、q=90%的试验验证过程，亦即系统通过试验验证的接受标准为以90%置信度验证系统满足不超过5%的失效/失败概率。由图2可知：在进行第18、49和78次试验时发生了失败，但这3次失败后，直到第133次试验均告成功，即累计试验133次中发生3次失败。这时，根据式(2)可以计算确定系统满足了失败概率不超过5%、置信度90%的设计要求。图2中显示，每次发生的失败都必须通过增加试验次数来作进一步验证，尤其首次失败将导致置信度的大幅下降。随着试验样本总数的增加，后续过程中再次发生失败对置信度的影响逐渐减小。

图2试验要求总次数随失败次数的增长规律(p=5%，
q=90%)
Fig. 2Required total number of tests grows as more failures occuring (p=5%, q=90%)

最终从第3次失败开始，到第133次试验均保持成功，此时可得到系统成功概率95%、置信度90%的结论。

2决策方风险与研制方风险

从前述(n，K)标准可知，在根据试验过程中的失败次数进行决策时，存在着系统实际运行时发生失效/失败的概率超过设计要求的风险。这可以理解为置信度问题，也可以理解为系统的固有失败概率大于设计值的问题。例如，通过前述n=133、K=3试验方案验证的系统，其实际失效/失败概率有10%的可能会大于5%。但另一方面，如果系统实际固有失败概率超过5%，比如当p=6%时，计算可知系统实际运行时发生少于3次失效/失败的可能性约为4%。这意味着由于被验证的系统或技术“运气”较好，虽然其固有性能并没有达到5%失效/失败概率的设计要求，但因为在133次试验中失败次数没有超过3次而被确认满足要求。这无疑给后续研制和系统集成带来了风险。这类风险同决策方基于试验结果判断系统是否满足设计要求相关，误判将可能导致决策失误，故可称其为决策方风险。

平行于上述风险，系统固有失效/失败概率也可能低于设计值。发生这种情况时，则存在着过度研发的风险，付出的代价是研制方投入过多的研发资源和更长的研发周期。对于高超声速飞行器等高风险研发项目而言，过度研发的风险给全系统研制带来的影响可能更大。

(3)

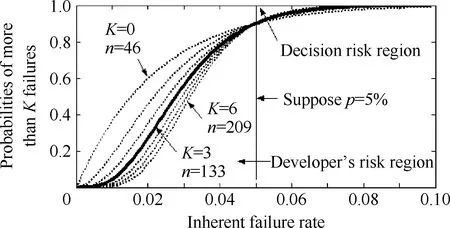
图3多于K次失败概率随p的变化规律
Fig. 3Probabilities of more than K failures versus p

3系统风险综合权衡

通过前文分析，可以明确在高风险项目研发中存在着决策方风险、研制方风险和时间周期风险等3类主要风险形式,如何进行三者间的权衡和优化直接关系到能否在有限资源和时间条件下取得最佳研发效果。为进一步量化分析三者的关系，定义研制方过度研发风险为

(4)

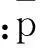
同理可以定义决策方风险为

(5)

式中：RA为决策风险，对应于图3中黑实线上方和5%概率线右侧所围成面积占5%概率线右边总面积的百分比。

针对给定的概率p和置信度q，可以计算得到RA和RD随试验样本或失败次数的变化规律。值得注意的是，试验总次数n的增长本身也意味着研制周期延误的风险在增大。

基于计算得到的决策风险、研制风险和周期风险，可以对高风险系统研发的综合风险进行权衡和优化。任何一类风险的增大或减小都直接体现在整体风险中。为说明这一概念，假设系统研制的整体风险可表达为这3项风险之和，而其中研制周期时间延误风险不妨直接以试验总次数为其量化指标，因此可将系统研发的综合风险RS定义为

RS=RD+ωARA+ωCRC

(6)

式中：RC为同研制周期时间延误相关的风险。考虑到研发周期时间同试验次数的相关性，可以认为其同试验总次数成正比，并定义为

RC=n/N

(7)

式中：N为研发计划预期的试验次数。根据式(3)，随着试验总次数n增大到接近甚至超过预期值N，研制周期风险将持续增大。为权衡考虑研制风险、决策风险和周期风险，可以引入各项风险的相对权重因子，式(6)中ωA和ωC分别为决策风险和周期时间风险相对于研制方风险的权重因子。

显然，ωA和ωC的取值直接关系到系统研发综合风险RS的大小。但注意到定义RS的意义在于给出了一种可以进行研制过程优化的量化方法，而这一优化方法的关键在于决策方和研制方之间合理地进行风险分担，使得研制工程的整体风险最小，片面强调减小某一方的风险都将导致系统研发综合风险的增大。因此，在确定风险权重因子时，需要考虑的是各方可接受风险的相对大小，以及对不同类型风险的控制对系统研发的重要程度。通过改变ωA和ωC的取值，可以调节决策方风险和研制周期风险相对于研制方过度研发风险的大小，从而可以适应不同系统研发中的具体情况。

图4显示了按式(4)、式(5)和式(7)计算得到的决策方风险和研制方风险随n、p和q的变化规律。由图4可知，随着试验总次数的增长，无论是决策方风险还是研制方风险都呈下降趋势，而随着p、q等设计目标值的变化，决策方风险和研制方风险的相对大小发生变化，尤其适当降低过高的失败概率设计目标p和q值，可以显著减小研制方过度研发的风险。

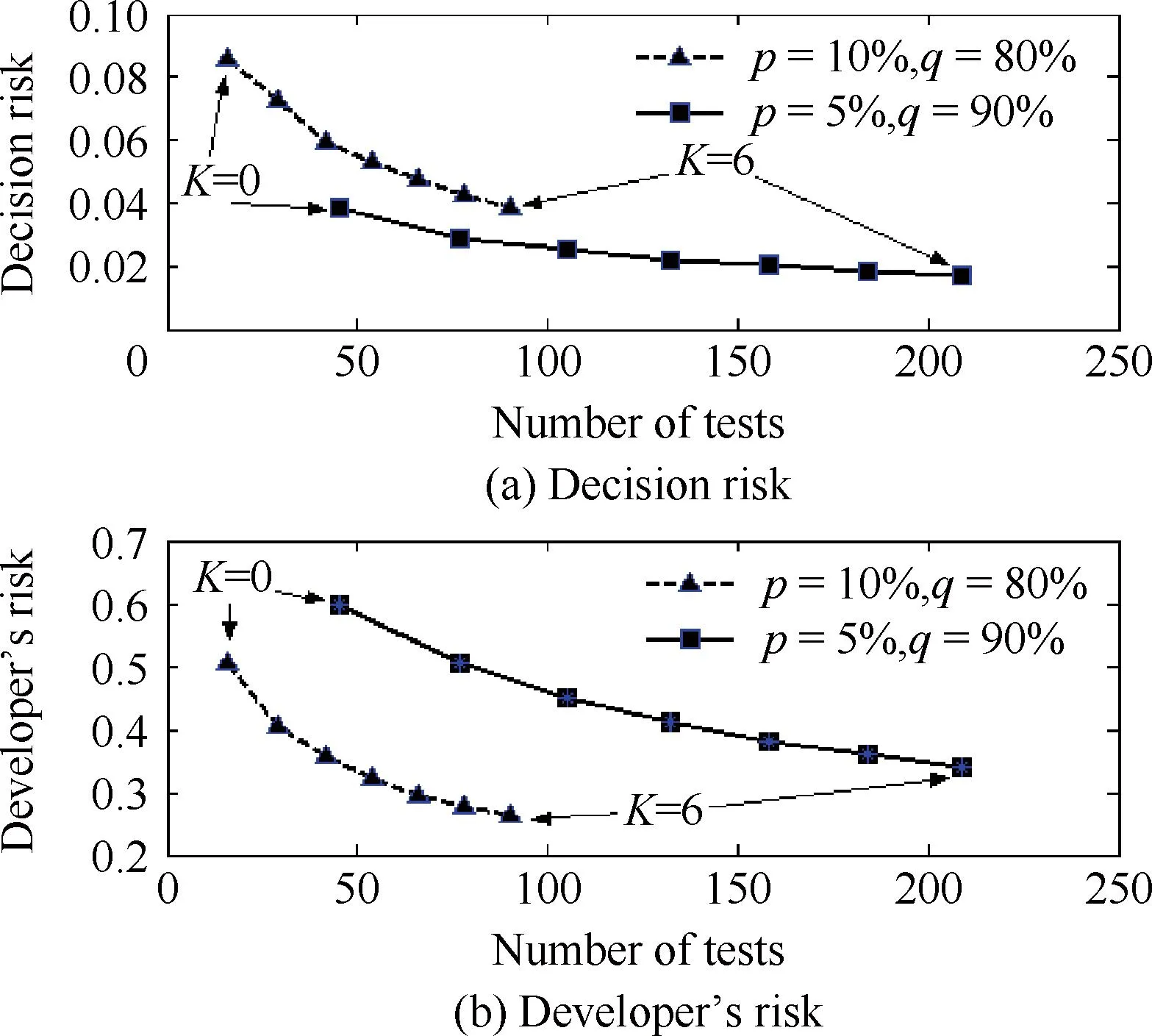
图4决策风险和过度研发风险变化规律
Fig. 4Variation patterns of decision risk and developer’s risk

表2和表3分别给出了采用不同的p和q设计值时的各类风险情况。取权重值为ωA=2、ωC=1，并取N=200，可以按式(6)得到系统研制综合风险值RS。注意到ωA、ωC和N的取值并不唯一，在此仅为说明相关概念。

表2　p=10%, q=80%时不同试验方案的风险

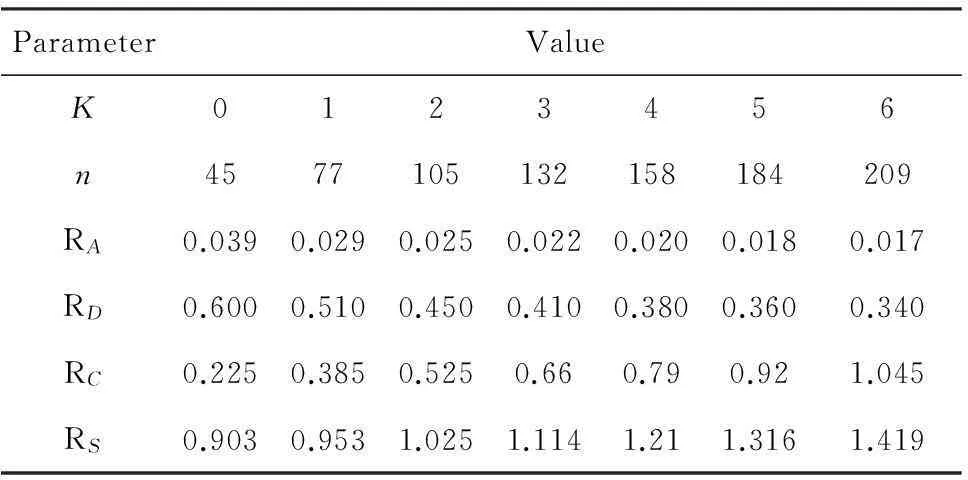
表3　p=5%,q=90%时不同试验方案的风险

表2和表3中的数据表明，对于基于式(6)的系统综合风险构成方式，系统固有风险设计参数(p、q)和试验方案(n，K)都对系统研发整体风险产生显著影响。合理地选择风险设计参数和试验方案，可以有效地降低系统综合风险。表中结果显示，当采用p=10%，置信度80%，累计42次试验中最多2次失败的方案可以获得显著优于其他方案的结果，系统综合风险值为0.686。值得注意的是，表2和表3结果并非意味着p越小系统综合风险就越小。事实上，当p进一步减小时，决策风险RA将快速增大，进而使系统综合风险RS增大。虽然不同类型的风险对系统综合风险的贡献取决于风险之间的权重关系，但上述分析和计算结果表明可以通过构建基于概率分析方法的数学模型，建立可用于优化权衡决策方、研制方及研制周期风险的系统工程量化方法。如何选择相关参数需要基于对单项风险的量化建模，如研制周期风险同试验次数的关系，决策风险代价和研制方投入成本之间的关系等。

4结论

高超声速飞行器研制是一项高风险的系统工程，其风险不仅存在于研制方是否能在给定的研制周期内攻克相关技术屏障，同时也存在于研制工程或计划决策方能否基于研制进展做出科学的判断和决策，动态地优化调节研制计划和验收标准。基于决策方风险、研制方风险及研制周期等3个方面因素的风险概率分析为高超声速飞行器研制系统工程提供了一种可行的优化方法。

参考文献

[1]张蒙正, 邹宇. 美国典型高超飞行器项目研发及启示[J]. 火箭推进, 2012, 38(2): 1-8.

ZHANG M Z, ZOU Y. Development of American typical hyper-sonic flight vehicles and its enlightenment[J]. Journal of Rocket Propulsion, 2012, 38(2): 1-8 (in Chinese).

[2]NASA Systems Engineering Handbook. NASA center for aerospace information： NASA/SP-2007-6105[R]. Washington, D.C.: NASA, 2007: 15-35.

[3]GRINFFIN M D. System engineering and the “Two cultures” of engineering (Boeing lecture presented at Purdue University)[R]. Lafayette: Purdue University, 2007: 1-3.

[4]徐志磊. 以科学为基础的复杂系统工程研制[J].中国工程科学, 2002, 4(10): 1-12.

XU Z L. Science-based engineering R & D of complex systems[J]. Engineering Science, 2002, 4(10): 1-12 (in Chinese).

[5]GRAVES R E. An analytics-based methodology for assessing aerospace system uncertainty to augment risk-informed systems engineering processes: AIAA-2013-0723[R]. Reston: AIAA, 2013.

[6]余后满, 林益明, 陈虎, 等. 航天器系统方案设计模式研究[J]. 航天器工程, 2010, 19(3): 1-6.

YU H M, LIN Y M, CHEN H, et al. Improved mode for spacecraft system scheme design[J]. Spacecraft Engineering, 2010, 19(3): 1-6 (in Chinese).

[7]SOLISH B, COOKE B, COX N, et al. Verification & validation by risk class: Understanding how risk classes affect the V&V process: AIAA-2013-5527[R]. Reston: AIAA, 2013.

[8]LUM C W, WAGGONER B. A risk based paradigm and model for unmanned aerial systems in the national airspace: AIAA-2011-1424[R]. Reston: AIAA, 2011.

[9]PATRIC S, SHAWN G, TIM G. Probabilistic risk analysis methodology on inadvertent laser illumination of satellite optical systems[J]. Journal of Spacecraft and Rockets, 2014, 51(6): 1994-2007.

[10]GAMBLE K B, LIGHTSEY E G. Decision analysis applied to small satellite risk management: AIAA-2015-1863[R]. Reston: AIAA, 2015.

[11]JIMENEZ H, SCHUTTE J, MAVRIS D. System readiness and risk assessment for advanced vehicle concepts-discussion of fundamental concepts: AIAA-2011-0423[R]. Reston: AIAA, 2011.

[12]沈小明, 张彤, 揭裕文. 航空产品研制阶段的技术性能风险研究[J]. 南京航空航天大学学报(社会科学版), 2014, 16(1): 64-71.

SHEN X M, ZHANG T, JIE Y W. Research on technical performance risk during aero-product development[J]. Journal of Nanjing University of Aeronautics & Astronautics (Social Sciences), 2014, 16(1): 64-71 (in Chinese).

[13]徐哲, 冯允成, 鲁大伟. 武器装备研制项目的技术风险评估[J]. 系统工程与电子技术, 2005, 27(6): 1123-1127.

XU Z, FENG Y C, LU D W. Appraisement model of technical risk for weapon system development[J]. Systems Engineering and Electronics, 2005, 27(6): 1123-1127 (in Chinese).

[14]SIEVERS M, MADNI A M. Defining “Credible Faults,” a risk-based approach: AIAA-2015-4528[R]. Reston: AIAA, 2015.

[15]ENRIGHT M P, LIANG W W. Development of risk contours for assessment of aircraft engine components: AIAA-2010-2846[R]. Reston: AIAA, 2010.

[16]BOUDALI H, SáNCHEZ A H. A conceptual design phase risk assessment methodology for space-based system of systems: AIAA-2010-8738[R]. Reston: AIAA, 2010.

[17]HAMLIN T L, THIGPEN E, KAHN J, et al. Shuttle risk progression: Use of the shuttle probabilistic risk assessment (PRA) to show reliability growth: AIAA-2011-7353[R]. Reston: AIAA, 2011.

[18]赵净净. 民用飞机研发过程中的权衡研究[J]. 科技创新导报， 2011(34)： 5-14.

ZHAO J J. Trade study of civil aircraft development [J]. Science and Technology Innovation Herald, 2011(34): 5-14 (in Chinese).

[19]HANSON J M, BEARD B B. Applying monte carlo simulation to launch vehicle design and requirements verification[J]. Journal of Spacecraft and Rockets, 2012, 49: 136-144.

[20]盛骤， 谢式千， 潘承毅.概率论与数理统计[M]. 北京： 高等教育出版社， 2001: 25-145.

SHENG Z, XIE S Q, PAN C Y. Probability theory and mathematical statistics[M]. Beijing： Higher Education Press， 2001: 25-145 (in Chinese).

沈作军男， 博士， 教授。主要研究方向： 高超声速飞行器系统研发, 临近空间制导控制技术， 飞行力学。

Tel: 010-82316572

E-mail: shenzuojun@buaa.edu.cn

柳青女， 高级工程师， 博士研究生。主要研究方向： 高超声速飞行器制导控制系统研制， 飞行控制技术。

Tel: 010-681920755

E-mail: liuliu_lock@126.com

肖佳平男， 硕士研究生。主要研究方向： 导航与制导技术， 临近空间大气环境建模。

Tel: 010-82316894

E-mail: xjpmail@126.com

Received： 2015-10-19; Revised: 2015-11-16; Accepted: 2015-11-22; Published online: 2015-12-0414:04

URL： www.cnki.net/kcms/detail/11.1929.V.20151204.1404.018.html

Probability-based risk analysis of hypersonic vehicle systems engineering

SHEN Zuojun1, *, LIU Qing2, XIAO Jiaping1

1. School of Aeronautic Science and Engineering, Beihang University, Beijing100083, China 2. The Third Research Institute, China Aerospace Science and Technology Corp., Beijing100074, China

Abstract:Different risks associated with decision party and system developer are modeled and analyzed aiming at the high risk characteristics of hypersonic vehicle development. Based upon the inherent probabilistic risks of system design and critical technologies, a generic test and verification process is adopted to calculate the probabilities of accepting unqualified systems by the decision party, or over-testing low risk systems or technologies by the developer. The relation between decision risk and developer’s risk is studied, and then a system engineering approach for balancing the risks as well as optimizing the development cycle is proposed based on probability calculation.

Key words:hypersonic vehicle; engineering development; developer’s risk; decision risk; risk probability; systems engineering optimization

*Corresponding author. Tel.： 010-82316572E-mail: shenzuojun@buaa.edu.cn

作者简介：

中图分类号：V37

文献标识码：A

文章编号：1000-6893(2016)01-0317-07

DOI：10.7527/S1000-6893.2015.0316

*通讯作者.Tel.： 010-82316572E-mail: shenzuojun@buaa.edu.cn

收稿日期：2015-10-19; 退修日期: 2015-11-16; 录用日期: 2015-11-22; 网络出版时间: 2015-12-0414:04

网络出版地址： www.cnki.net/kcms/detail/11.1929.V.20151204.1404.018.html

引用格式： 沈作军， 柳青， 肖佳平． 高超声速飞行器研制系统工程风险概率分析[J]． 航空学报, 2016, 37(1): 317-323. SHEN Z J, LIU Q, XIAO J M. Probability-based risk analysis of hypersonic vehicle systems engineering[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 317-323.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn