组合波阻技术的波动力响应矩阵分析法及其特性研究

林永水，吴卫国，甘 进

（武汉理工大学 a.交通学院；b.理学院，武汉430070）

组合波阻技术的波动力响应矩阵分析法及其特性研究

林永水a，b，吴卫国a，甘 进a

（武汉理工大学 a.交通学院；b.理学院，武汉430070）

基于有限元思想，综合运用波分析法和阻抗法，提出了波阻元件阻抑结构声传递的波动力响应矩阵分析法。将结构离散为多个波导单元和波阻单元，根据连接节点的位移连续，力与力矩平衡，建立附加波阻元件的结构连接广义波动力响应平衡方程，推导出波单元波动力响应特征矩阵及波阻元件附加波动响应特征矩阵，并代入波动力响应平衡方程求解得到波单元的振动幅值，从而求得传递效率与损失。运用该方法对阻振质量，粘弹性夹层以及动力吸振器的波阻特性进行了数值分析。最后，重点分析了组合波阻技术的波阻特性。研究表明，根据不同类型波阻元件的波阻特性，进行科学的组合与优化布置，并选择合理的设计参数，能显著提高组合波阻元件的阻抑效果。以上研究为组合波阻元件的声学设计提供了分析方法及新的控制策略，在舰船等结构减振降噪中具有重要的理论意义与工程应用价值。

结构声；波分析法；组合波阻技术；阻振质量；粘弹性夹层；动力吸振器

0 引 言

由于船舶大多数是薄壁钢质结构，材料的阻尼系数低，结构的连续性好，是结构声传播的优良导体，如何有效抑制结构声的传递是舰船振动噪声控制的重要研究内容。波阻技术是一项重要的控制技术，常用的波阻技术有阻振质量、粘弹性夹层以及动力吸振器等[1-2]。

刘见华等[3]研究了半无限板连接附加阻振质量对结构声传递的阻抑，揭示入射平面弯曲波发生最大透射的条件是板的平面弯曲波分别与阻振质量的弯曲波和扭转波达到最佳耦合；其还用波动分析法研究了多个平行排列的阻振质量阻抑结构声传递机理，找到了弯曲波传播时形成的穿透频段和堵塞频段，并进行试验验证[4]。石勇等[5-6]从质量引起的阻抗失配的原理出发，利用波分析法探讨了在板中嵌入一块方钢对振动波传递的阻碍作用，并且通过数值仿真和实验对比研究，检验了方钢的阻抑效果。车驰东等[7-8]运用波分析法和实验方法探讨附加在转角处的阻振质量对结构波传递的阻抑作用。易太连等[9]运用波分析法研究了刚性质量块的减振机理，对其减振效果进行了理论分析。钱德进，姚熊亮等[10-13]采用波分析法，探讨了振动波入射设有单级以及多级阻振质量的结构中的传递特性，讨论了阻振质量对T型板以及L型板中弹性波传递的影响，推导了阻振质量的传递系数和隔振度公式；还进一步探讨阻振质量偏心布置对其隔振性能的影响，并开展双层壳动力舱段阻振质量刚性隔振特性研究。车驰东等[14]运用波分析法研究多转角附加阻振质量对结构波传递的抑制影响，但其忽略了近场波的影响，且分析复杂。Cremer等[1]对粘弹性夹层做了深入的理论分析和数值研究，探讨了弹性夹层特征参数对传递特性的影响。计方和夏齐强等[15-16]分别对阻振质量与粘弹性夹层组合使用的波阻特性进行了理论与数值分析和应用研究，但并没有考虑波在阻振质量与粘弹性夹层之间的相互反射，推导认为传递损失是两者的线性相加有待商榷，此外，其分析模型并不适用于波阻元件之间有一定间距的情况。车驰东[17]对动力吸振器阻抑结构声特性进行了理论、数值和实验研究，揭示动力吸振器能增大特定频段的传递损失。韩彬[18]对动力吸振器阻抑结构声传递进行了理论分析与数值研究，认为动力吸振器质量增加，传递损失增大。

目前对组合波阻技术的波阻抑特性研究较少，且波分析模型没有全面统一考虑各种因素，如波阻元件的类型，布置方式与间距，材料与厚度比，连接转角及近场效应等。因此，提出一种可用于不同波阻元件波阻特性的分析方法，是亟需解决的难题，建立适用于不同波阻元件的统一力学分析模型和广义波动力响应平衡方程是解决此难题的关键技术。研究将对结构声起传导作用的板、梁以及壳等定义为波导结构，对结构声传导起阻抑作用的附加元件定义为波阻元件。在结构不连续处将其离散为多个波导单元和波阻单元，并根据连接节点的位移连续，力与力矩平衡，建立附加波阻元件的广义波动力响应平衡方程。以波导单元的波响应幅值为状态参数，推导出波单元的波动力响应及波阻元件的附加波动响应特征矩阵，代入平衡方程，求解得到波单元的位移幅值，进而求出传递效率、传递损失及插入损失。方程的建立是以单元波动力响应为变量，因而不受波导单元的具体参数、波阻元件的类型及参数限制，克服了以往研究单独求解各种波阻元件而不能线性叠加的缺陷。波动力响应矩阵法将不同波阻元件阻抑结构声传递问题的求解转化为线性代数方程组的求解，降低了求解复杂性。研究揭示波单元和波阻元件的特征矩阵具有唯一性，由其自身特性决定。在阻振质量、粘弹性夹层以及动力吸振器的波阻特性数值分析基础上，将重点探讨组合波阻元件的波阻特性，为组合波阻技术在舰船等结构的减振降噪应用提供分析方法和建议。

1 波阻元件波阻特性理论分析

1.1 力学分析模型及平衡方程

如图1所示，n+1平板，其中两板任意角连接，在板i左端建立局部坐标系xiyizi，βi+1为板i和板i+ 1的连接转角，定义为板i顺时针绕yi+1轴与板i+1重合所转过的角度。板1和板n+1在x方向上为半无限长，其它为有限长，所有板在y方向上均为无限长。图中B表示弯曲波，L表示纵波。li表示板在xi方向的长度。波阻元件（R）布置在连接处，常见的有阻振质量，粘弹性夹层以及动力吸振器等。板及其中传播的波构成一个波单元。

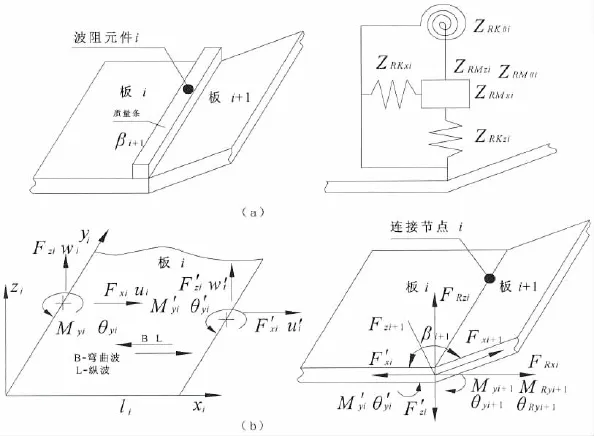
图1 （a）分析模型及等效模型；（b）单元波动力响应及节点力与力矩Fig.1(a)Analysis model and Equivalent model;(b)Dynamic response of element and forces,moments of node

当弹性波法向入射时，假定经过多次反射和透射后，可分成沿正向和负向传播的波，同一方向上的波叠加后能量总和是一个有限值，满足收敛条件[1，17]，可用ξ+Li，ξ+Bi，ξ+BNi分别表示波单元i中正向传播的纵波、弯曲波以及近场衰减弯曲波幅值，ξ-Li，ξ-Bi，ξ-BNi分别表示波单元i中负向传播的纵波、弯曲波以及近场衰减弯曲波幅值。根据以上假设，波单元i的面内纵波及面外弯曲波在坐标系xiyizi表示为：

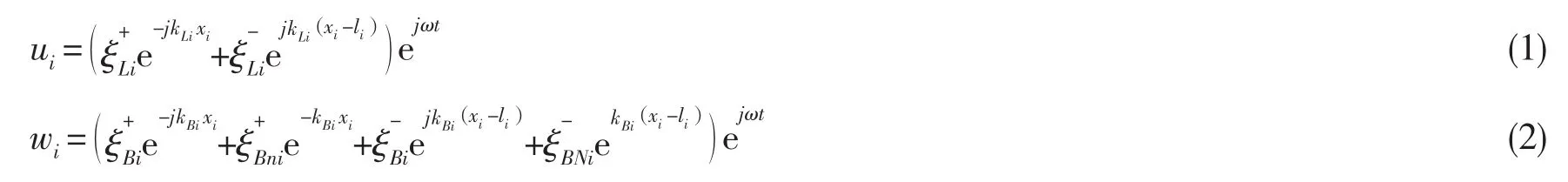
当弹性波法向入射时，角位移、力和力矩（单位宽度）可按下式求解[19]：

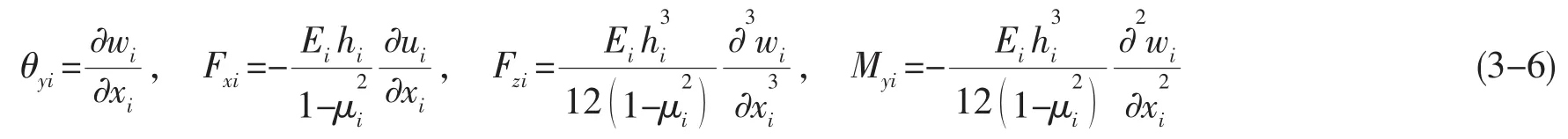
以下推导了省略时间简谐因子项ejωt。

当波阻元件为阻振质量（M），根据位移连续，力与力矩平衡，连接处节点有以下平衡方程：

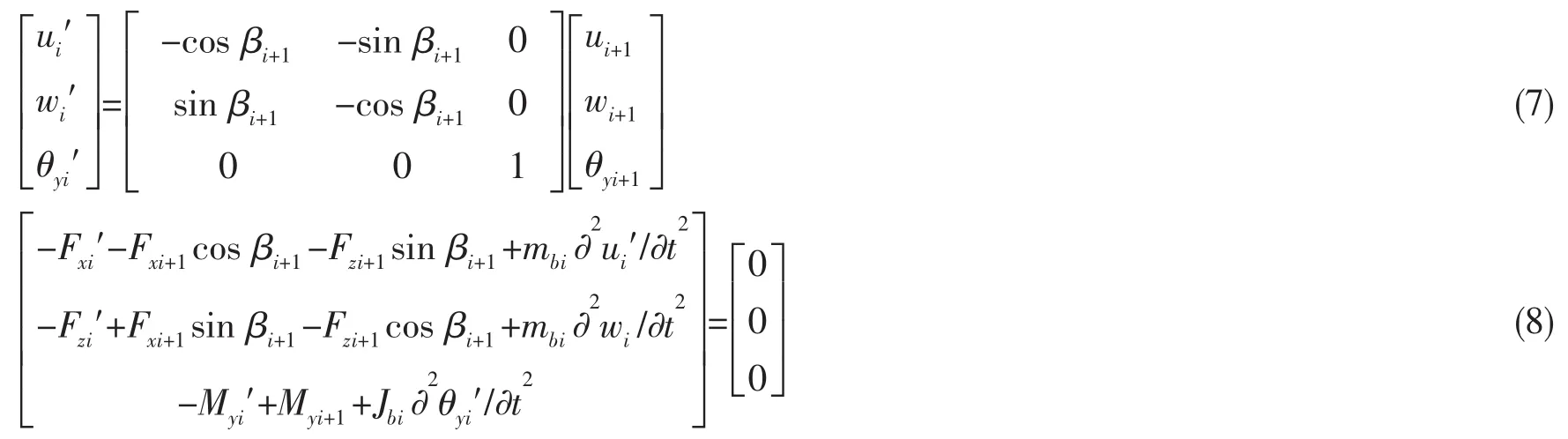
式中：mbi为波阻元件i单位长度质量，Jbi为相应的转动惯量。

当波阻元件为粘弹性夹层（C），根据位移连续，力与力矩平衡，连接处节点有以下平衡方程：

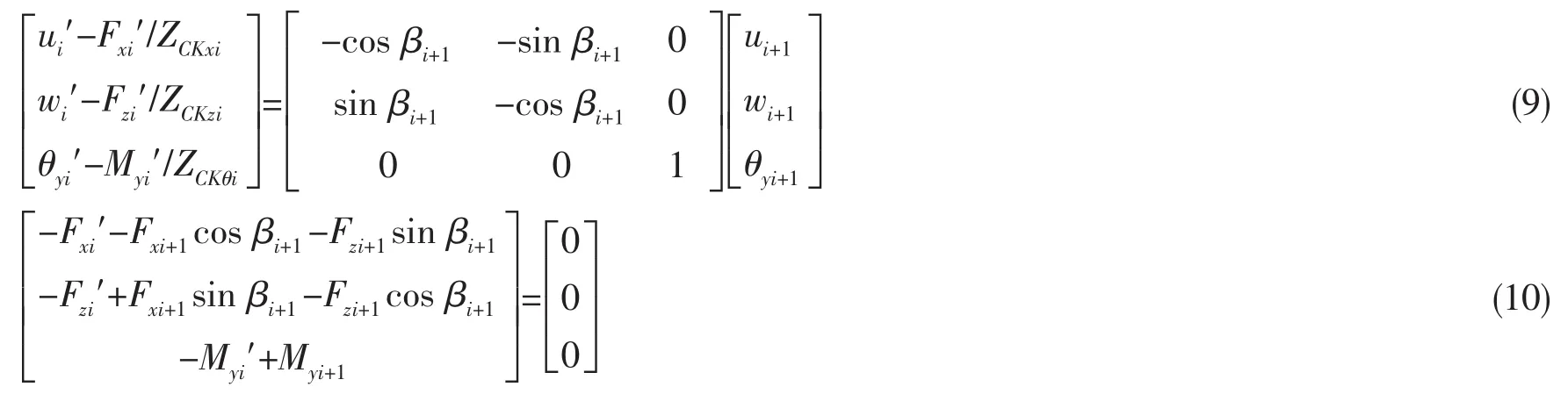
式中：ZCKxi，ZCKzi及ZCKθi分别为波阻元件i在x，z方向的弹性力阻抗及绕y方向的弹性力矩阻抗，其中，分别为波阻元件的弹性模量，泊松比，长度、高度及阻尼损耗因子。

当波阻元件为动力吸振器（A），根据变形连续，力与力矩平衡，连接处节点有以下平衡方程：

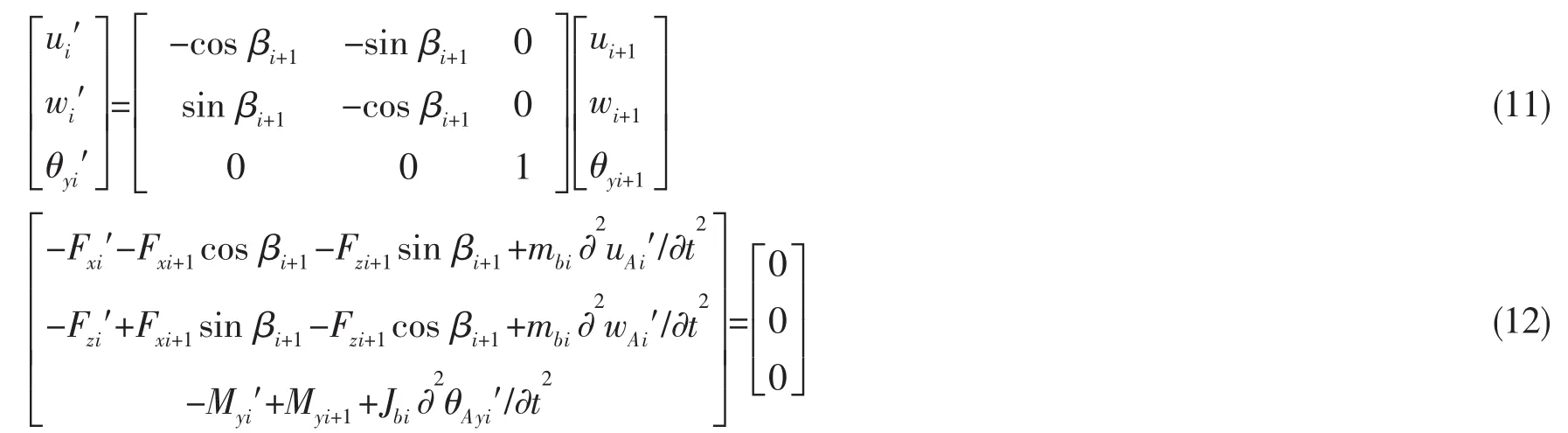
对波阻元件还有以下力与力矩平衡方程：

式中：ZAKxi，ZAKzi及ZAKθi分别表示波阻元件i在x，z方向的弹性力阻抗及绕y方向的弹性力矩阻抗；其中及 ηAi分别是弹性层i的弹性模量，泊松比，高度，长度以及阻尼损耗因子。

1.2 波动力响应平衡方程

波单元i在xi=0和xi=li处的响应为PDi和PDi′，波阻元件i在xi=li处的响应为PRi′，分别用下式表示：

根据前面的分析，布置波阻元件后，在连接处，满足位移连续，力与力矩平衡方程，因而可得附加波阻元件连接的广义波动力响应平衡方程：

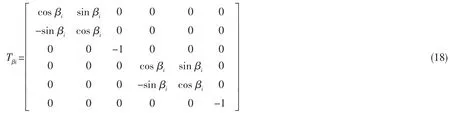
波单元与波阻元件的附加波动力响应矩阵存在以下的对应关系：

将（19）式代入（17）式，得到关于波单元波动力响应的广义平衡方程：

1.3 波单元波动力响应

根据（1）式和（2）式，设波单元i的状态未知量为：

波单元i的波动力响应PDi和PDi′与δi之间存在以下关系：

式中：fDi是入射波引起的波动力响应。Kei为波单元波动响应固有特征矩阵，与单元结构属性有关，为6×6的矩阵，其各个元素为：

自2010年起，部分房地产估价机构先后开启了信息化探索之路，并取得了一定成果。主要分为两种类型：一类为独立运营，较为典型的有深圳世联、深圳国策、深圳评估中心、北京国信达等；另一类为联盟运营，较为典型的有中估联行、中房评、恒基数据、云估价、云房等。不管是独立运营，还是联盟运营，各房地产估价机构都致力于自动估价系统、知识管理系统、业务流程系统、自动办公系统、押品重估系统、不动产运营管理系统、投贷后资金管理服务系统等信息产品的开发与应用，以进一步提升传统业务服务效率和不断开拓新型业务发展空间，也对行业面临的现状困境起到了一定的改善作用。

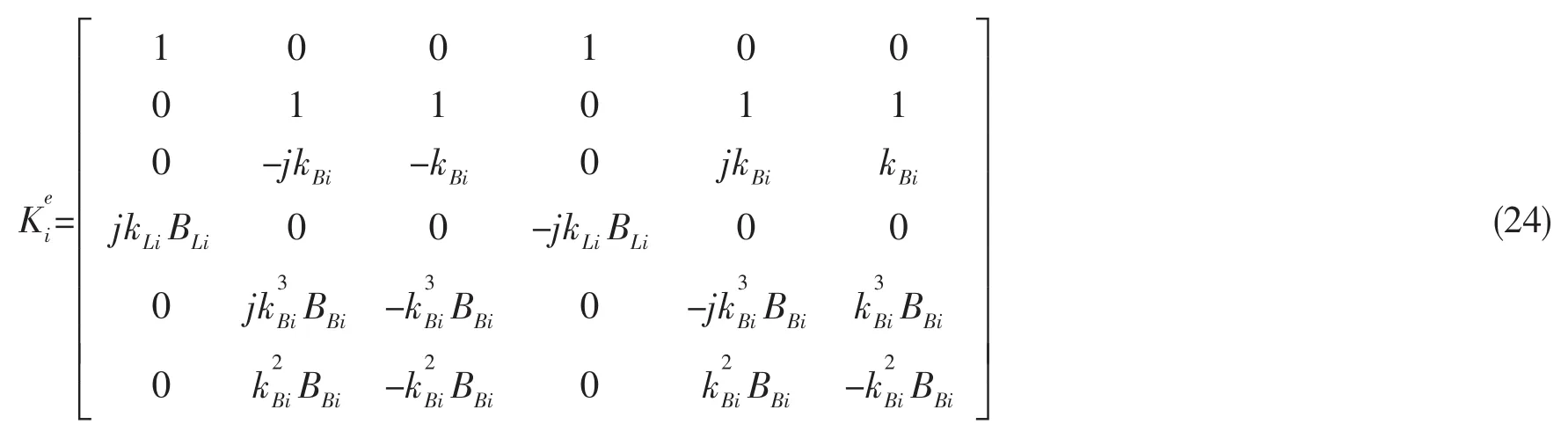
1.4 波阻元件附加波动力响应

式中：fRi′为入射波引起的波阻元件产生的附加波动力响应。

根据（7）式，（8）式及（20）式，可推导出阻振质量的附加波动力响应特征矩阵，具体如下：

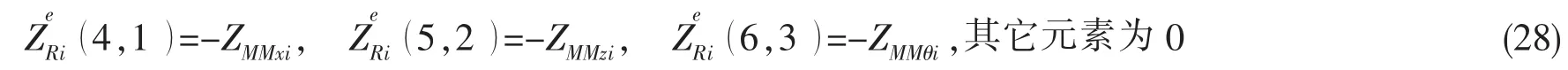
根据（9）式，（10）式及（20）式，可推导出粘弹性夹层的附加波动力响应特征矩阵，具体如下：

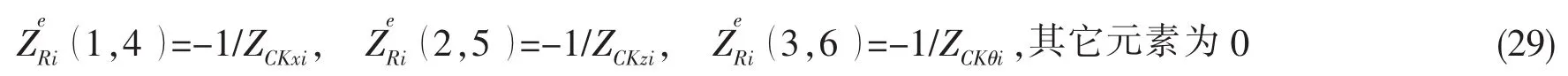
根据（11）-（13）式及（20）式，可推导出动力吸振器的附加波动力响应特征矩阵，具体如下：

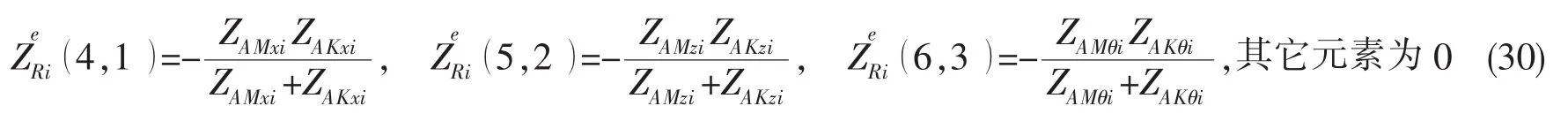
1.5 入射波波动力响应

当单位幅值的弯曲波和纵波分别法向入射波单元1时，在坐标系x1y1z1中可用下式表示：

入射波引起波单元右端产生的波动力响应分别为：

入射波引起阻振质量产生的附加波动力响应为：

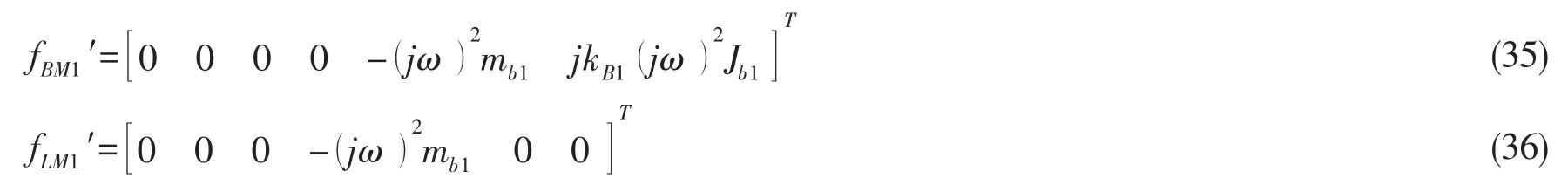
入射波引起粘弹性夹层产生的附加波动力响应为：

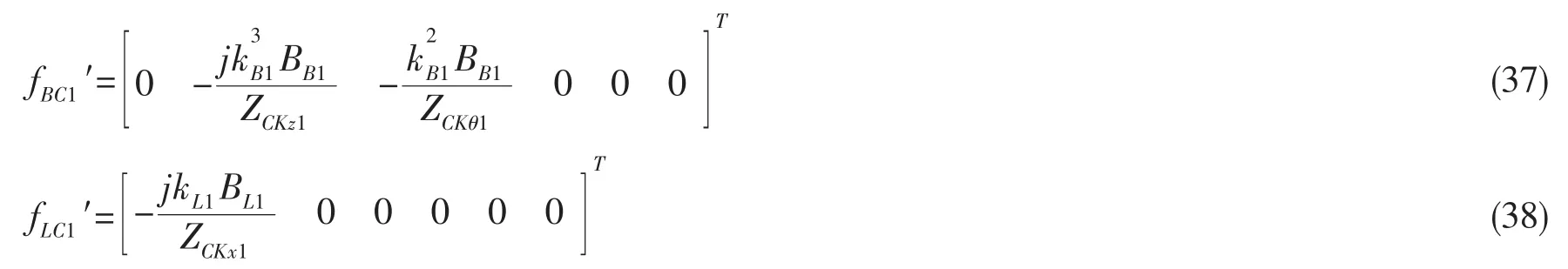
入射波引起动力吸振器产生的附加波动力响应分别为：

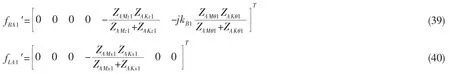
1.6 波动力响应平衡方程求解

将（22）式、（23）式及（27）式代入方程（20），可得到以波单元幅值为状态未知量的平衡方程，其为

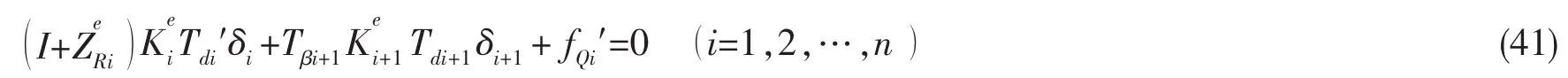
1.7 传播效率与传递损失

假设入射波的幅值为1，入射波，透射波（+）及反射波（-）的输入功率（单位长度板宽）分别为：

沿正向和负向传播的波的传递效率及传递损失分别如下：

式中：m″为波单元的面密度，cgDi代表波群速度，有cgBi=2cBi，cgLi=cLi；Q，D同上。cBi，cLi分别为弯曲波和纵波的相速度。

2 数值仿真研究

2.1 阻振质量波阻特性

图2与文献[1]中公式（190）和公式（209）计算的结果相同，证明了本方法用于阻振质量阻抑特性分析的可靠性。图2和文献[1]中图Fig.V/15存在细微差异，主要原因是阻振质量的材料参数取值不同。文献[1]关于临界波长的计算公式（208）对图4中的模型分析，可得弯曲波临界波长λB=0.34 m，全衰减频率为1 670 Hz，与图2反映的一致。数值仿真表明，图2模型中的能量传递系数之和为1，满足能量守恒。

数值仿真表明，增大阻振质量单位长度质量或者减小其转动惯量，传递损失极大值往高频移动，极小值往高频移动，为了增大整个频域的阻抑效果，尽可能提高阻振质量的惯性半径定义是否有阻振质量的传递损失之差为插入损失，插入损失为0所对应的频率为阻抑临界频率。图3揭示，当频率小于阻抑临界频率，其增大结构的声振传导性；当频率大于临界阻抑频率，其起到阻抑作用。当转角不等于180°，其增大结构中低频段的声振传导性，因此，在阻振质量设计时，最好将其布置在线形连接处。

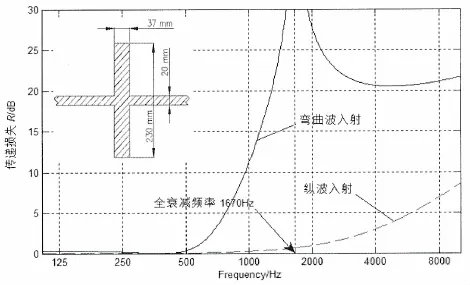
图2 附加能阻振质量传递损失（mb=66.8 kg/m，Jb=0.302 kg·m）Fig.2 Transmission loss of a blocking mass

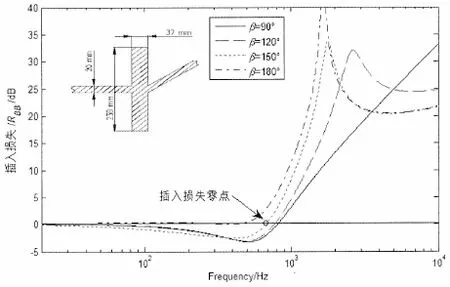
图3 附加阻振质量不同转角下弯曲波传递插入损失（mb=66.8 kg/m，Jb=0.302 kg·m）Fig.3 Bending wave transmission insertion loss of a blocking mass with different angles

2.2 粘弹性夹层波阻特性

图4所示结果与文献[1]（p374）基本一致，此外，数值仿真表明，图4模型中的能量传递系数之和为1，满足能量守恒，以上分析验证了本方法用于粘弹性夹层阻抑结构声传递分析的可靠性。结果有细微差异的主要原因是文献[1]推导时假定软木阻抗与混凝土阻抗之比近似为0，公式推导做了一定简化。

数值仿真揭示随着弹性模量的增大，全透射频率向高频移动；随着粘弹性夹层长度的增大，全透射频率向低频移动。图5揭示转角对粘弹性夹层在低频段的阻振效果产生明显影响，当转角为90°时，粘弹性夹层对弯曲波的阻抑效果会显著提高。因此，在粘弹性夹层声学设计时，最好将其布置在L形连接处。

表1 材料参数[1]Tab.1 Parameters of materials

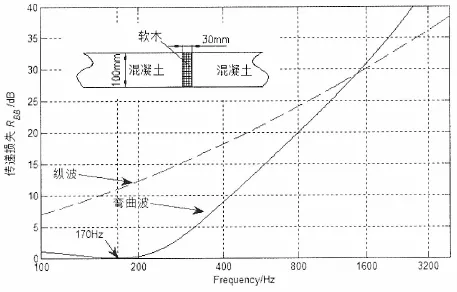
图4 附加粘弹性夹层的能量传递损失Fig.4 Transmission loss of an elastic interlayer

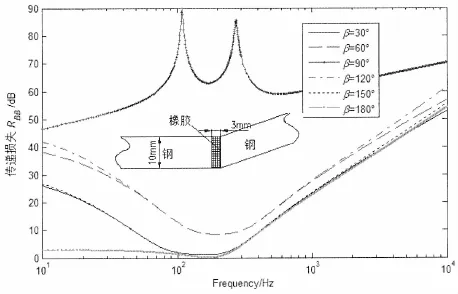
图5 附加粘弹性夹层不同夹角的弯曲波传递损失Fig.5 Bending wave transmission loss of an elastic interlayer with different intersection angles

2.3 动力吸振器波阻特性

图6给出两块15 mm厚钢板成135°转角的连接结构，在其连接处安装动力吸振器的弯曲波传递效率，其和为1，满足能量守恒。根据文献[17]，可以得到动力吸振器三个自由度上的固有频率，分别为831 Hz，1 518 Hz和1 073 Hz。τBB并没有在频率1 518 Hz和1 031 Hz附近取得极小值。分析认为，激励频率等于固有频率时，动力吸振器与板连接处的位移为零，动力吸振器的位移是一个有限值，由方程（12）决定。尽管在动力吸振器固有频率点，其对连接节点的振动抑制效果达到最佳，但对波传递的阻抑效果并不是最佳，最佳波阻效果由动力吸振器、板的属性及连接转角共同决定。

数值仿真进一步揭示随着弹性模量的增大，动力吸振器的传递损失极小值和极大值均向高频移动；随着质量的减小或转动惯量的增大，传递损失极大值和极小值均向低频移动，因此增大惯性半径，可以提高中频段的波阻效果。图7反映阻尼系数对动力吸振器传递损失极大值影响较大，随着阻尼系数增大，极大值降低，因为阻尼的存在将使得板的部分能量被吸收，从而导致传递损失极大值下降。以上数值分析表明动力吸振器在中间某一频段内具有显著的波阻效果。

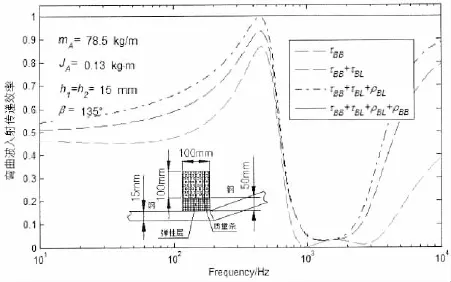
图6 附加动力吸振器的弯曲波能量传递效率（EA=3×109N/m2，μA=0.5）Fig.6 Transmission efficiency of bending wave for a dynamic vibration absorber

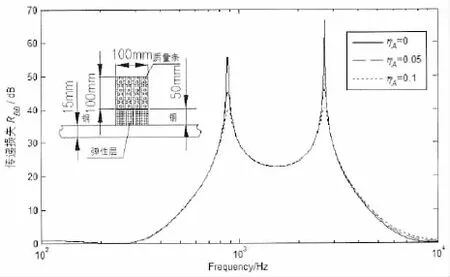
图7 附加动力吸振器不同阻尼系数的弯曲波传递损失（mb=78.5 kg/m，Jb=0.13 kg·m，EA=3×109N/m2，μA=0.5，β=180°）Fig.7 Bending wave transmission loss with different loss factors for dynamic vibration absorbers

2.4 组合波阻元件波阻特性

图8给出了阻振质量，粘弹性夹层以及动力吸振器两两组合的波阻特性，其中阻振质量和动力吸振器质量块的高度和宽度为50 mm，粘弹性夹层的高度为25 mm，宽度为50 mm，材料为“28gray橡胶”，参数见表1。波阻元件的间距为500 mm，钢板厚度为5 mm，连接转角分别为180°（线形连接）和90°（L形连接）。图8表明，合理布置波阻元件对提高整个频段的波阻效果至关重要，“阻振质量+粘弹性夹层”或者“动力吸振器+粘弹性夹层”组合使用时在整个频段的波阻效果均较好，既能发挥阻振质量的高频段的波阻优势，又能发挥粘弹性夹层在转角为90°时的波阻效果。根据前面分析可知，各种波阻元件都有自己的波阻频域特性和转角特性，单独使用某一种波阻元件，在某一频段波阻效果较差，采取组合波阻技术，可最大限度发挥各种波阻元件的波阻优势，既能提高特定频段的波阻效果，又能提高整个频段的综合波阻效果。数值分析进一步表明，各个波阻元件的特征参数也会对组合波阻技术的综合波阻特性产生影响。根据激励频率，合理选择波阻元件及其参数，可有效增大动力设备的声振传递损失，提高减振降噪效果。

当不同波阻元件之间的布置间距为0时，此时他们构成了复合波阻元件，图9分别给出了钢制阻振质量（其截面尺寸为100 mm×100 mm）、动力吸振器（其质量条截面尺寸为100 mm×100 mm，粘弹性夹层尺寸为100 mm×50 mm，EA=5.4×107N/m2，μA=0.5，ηA=0）以及其构成的组合波阻元件的弯曲波传递损失。分析可知，布置组合波阻元件后整个结构的传递效率之和为1，满足能量守恒；其次，但波从阻振质量连接的半无限板入射和从动力吸振器连接的半无限板入射，有满足互异性；侧面验证了本方法的可靠性。进一步分析可知，组合波阻元件阻抑效果不是简单的线性叠加，而是两者构成一个整体，共同阻抑波的传播，布置合理，将发挥“1加1大于2”的波阻效果，同时能避免结构固有特性对弹性波传播的影响，能显著提高中低频段的波阻效果。

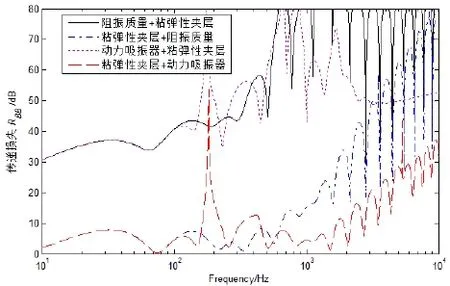
图8 组合波阻元件的弯曲波传递损失Fig.8 Bending wave transmission loss of different composite wave impedance facilities

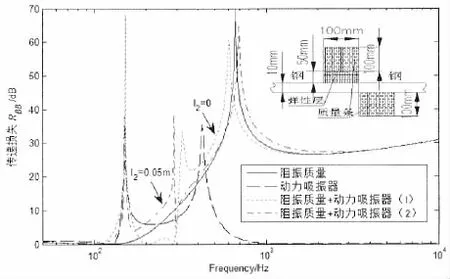
图9 不同复合波阻元件的弯曲波传递损失Fig.9 Bending wave transmission loss of different composite wave impedance facilities

3 结 论

（1）研究为组合波阻元件的结构声传递阻抑特性提供了一种新的分析方法，扩大了波分析法的应用范围及简化了求解。阻振质量具有很好的高频波阻效果，增大惯性半径传递损失极大值向低频移动；粘弹性夹层具有较好的高频波阻效果，在低频段也具有一定的波阻效果，减小弹性模量，增大其长度，传递损失极小值向低频移动，从而提高中频段的波阻效果；动力吸振器在特定的中频段具有显著的波阻效果。结构连接转角对波阻元件的阻抑特性影响较大，阻振质量布置在线形连接处，粘弹性夹层布置在L形连接处，更能发挥其波阻作用。

（2）采用组合波阻技术，根据不同类型波阻元件的波阻特性，进行合理组合，科学选择波阻元件的设计参数并采取合理的布置方式，能有效拓宽波阻频带，尤其是改善中低频的波阻抑作用，从而提高整个频域的波阻效果。采用“动力吸振器+阻振质量”，既能保证具有高频波阻效果，还能提高局部特定频段的阻抑效果，其对动力舱的结构噪声的传递控制具有重要应用价值。采用“阻振质量+粘弹性”复合波阻技术可有效提高整个频段的波阻效果，对于非主要承载构件的结构声传递控制具有实际应用背景。

[1]Cremer L,Heckl M,Ungar E E.Structure-borne sound,first edition[M].Berlin:Springer-Verlag,1988.

[2]尼基福罗夫.阿.斯.船舶结构声学设计[M].北京:国防工业出版社,1998. Nikiforov A C.Acoustic design of ship hull structure[M].Beijing:National Defense Industry Press,1998.

[3]刘见华,金咸定,李 喆等.阻振质量阻抑结构声的传递[J].上海交通大学学报,2003,37(8):1201-1204. Liu Jianhua,Jin Xianding,Li Zhe,et al.Impediment to structure-borne sound propagation from vibration isolation mass [J].Journal of Shanghai Jiaotong University,2003,37(8):1201-1204.

[4]刘见华,金咸定.多个阻振质量阻抑结构声的传递[J].上海交通大学学报,2003,37(8):1205-1212. Liu Jianhua,Jin Xianding.Impediment to structure-borne sound propagation from several paralleling arranged vibration isolation mass[J].Journal of Shanghai Jiaotong University,2003,37(8):1205-1212.

[5]石 勇,朱 锡,胡忠平等.方钢刚性减振结构对组合板振动影响的计算分析[J].海军工程大学学报,2003,15(2): 45-49. Shi Yong,Zhu Xi,Hu Zhongping,et al.Influence of quadrate steel beam with vibration-damping structure on vibration of combined plates[J].Journal of Naval University of Engineering,2003,15(2):45-49.

[6]石 勇,朱 锡,刘润泉等.方钢隔振结构对结构噪声隔离作用的理论分析与试验[J].中国造船,2004,45(2):36-42. Shi Yong,Zhu Xi,Liu Runquan,et al.Analysis and experimental research on the role of quadrate steel beam in isolating vibration wave[J].Shipbuilding of China,2004,45(2):36-42.

[7]车驰东,陈端石.成任意角度连接的两块平板转角处阻振质量对平面弯曲波传递的影响分析[J].声学学报,2007,32 (3):282-288. Che Chidong,Chen Duanshi.Analysis of the effect of blocking mass at corner interface of two plates at arbitrary angles on transmission of plane bending waves[J].Chinese Journal of Acoustics,2007,32(3):282-288.

[8]车驰东,陈端石.转角处阻振质量对平面纵波—弯曲波传递衰减作用的研究[J].船舶力学,2011,15(1):132-142. Che Chidong,Chen Duanshi.Attenuation effect of blocking mass attached at corner interface on transmission from plane longitudinal wave to bending wave[J].Journal of Ship Mechanics,2011,15(1):132-142.

[9]易太连,欧大生,欧阳光耀等.刚性隔振装置设计和隔振效果试验研究[J].振动与冲击,2008,27(1):169-173. Yi Tailian,Ou Dasheng,Ouyang Guangyao,et al.Design and experimental analysis of a rigid block isolator[J].Journal of Vibration and Shock,2008,27(1):169-173.

[10]姚熊亮,钱德进,张阿漫等.刚性阻振降噪技术的应用研究及发展[J].中国舰船研究,2008,3(5):1-6,12. Yao Xiongliang,Qian Dejin,Zhang Aman,et al.Survey and tendency of study on rigid vibration-isolating technique[J]. Chinese Journal of Ship Research,2008,3(5):1-6,12.

[11]钱德进,姚熊亮,计 方等.多级阻振质量阻隔振动波的传递特性研究[J].应用声学,2009,28(5):321-329. Qian DeJin,Yao Xiongliang,Ji Fang,et al.Impending vibration wave propagation from several arranged vibration isolation masses[J].Applied Acoustics,2009,28(5):321-329.

[12]姚熊亮,计 方,钱德进等.舰船阻振质量刚性隔振特性研究[J].中国舰船研究,2010,05(5):15-21. Yao Xiongliang,Ji Fang,Qian Dejin,et al.Rigid vibration isolation characteristics of ship blocking masses[J].Chinese Journal of Ship Research,2010,05(5):15-21.

[13]姚熊亮,计 方,钱德进等.偏心阻振质量阻抑振动波传递特性研究[J].振动与冲击,2010,29(1):48-52. Yao Xiongliang,Ji Fang,Qian Dejin,et al.Characteristics of eccentric blocking mass attenuating vibration wave propagation[J].Journal of Vibration and Shock,2010,29(1):48-52.

[14]车驰东,陈端石.多转角结构中转角处附加的阻振质量对结构波传递的抑制[J].船舶力学,2010,14(9):1052-1064. Che Chidong,Chen Duanshi.Structure-borne sound attenuation in a multi-corner structure with attached blocking masses[J].Journal of Ship Mechanics,2010,14(9):1052-1064.

[15]计 方,路晓东,姚熊亮.船体结构粘弹性夹层阻抑振动波传递特性研究[J].应用基础与工程科学学报,2012,20(3): 464-471. Ji Fang,Lu Xiaodong,Yao Xiongliang.Research on hull structure elastic interlayer impending vibration wave propagation[J].Journal of Basic Science and Engineering,2012,20(3):464-471.

[16]夏齐强,陈志坚,林超友等.双层壳舷间复合阻波托板结构声学设计[J].中国造船,2013,54(4):28-36. Xia Qiqiang,Chen Zhijian,Lin Chaoyou,Wang Jun.Structure-borne sound design of composite wave attenuation brace between double cylindrical shell[J].Shipbuilding of China,2013,54(4):28-36.

[17]车驰东.动力设备结构声传递的理论分析及阻波技术的研究[D].上海:上海交通大学,2008. Che Chidong. Theoretical analysis on transmission and attenuation of structure-borne sound generated by power machineries[D].Shanghai:Shanghai Jiaotong University,2008.

[18]韩 彬.基于动力吸振器的结构声传递抑制[D].武汉:华中科技大学,2006. Han Bin.Impediment to structure-borne sound propagation using vibration absorbers[D].Wuhan:Huazhong University of Science and Technology,2006.

[19]Love,A E H.A treatise on the mathematical theory of elasticity[M].Cambridge:Cambridge University Press,2013.

A wave dynamic response matrix method for solving problems about impeding structure-borne sound transmission from composite wave impedance technique

LIN Yong-shuia,b,WU Wei-guoa,GAN Jina
(a.School of Transportation;b.School of Science,Wuhan University of Technology,Wuhan 430063,China)

This paper proposes a wave dynamic response matrix method to investigate the problem of impeding structure-borne sound transmission from wave impedance facilities based on the wave approach, impedance method and finite element idea.The structure is discretized into many wave elements and a general wave dynamic response equilibrium equation is developed according to the displacement compatibility, force and moment equilibrium at the junction node.And,the wave dynamic response matrices of wave elements and the added wave dynamic response matrices of wave impedance facilities are deduced.The vibration amplitudes of wave elements are obtained by resolving the equilibrium equation and the transmission efficiencies and transmission loss are then obtained.The method is illustrated by a series of wave attenuation models such as blocking mass,elastic interlayer and dynamic vibration absorber.Finally,numerical analysis focuses on the attenuation of structure-borne sound through the composite wave impedance facilities.The numerical simulation results show that the wave transmission loss of the whole frequency domain will be greatly improved by using composite wave impedance technique with reasonable selection of design parameters and the optimal layout.This study provides a new analysis method for the structural acoustic design of composite wave impedance facilities and a new kind of control policy,which has great theoretical significance and important value for engineering application in the field of noise and vibration reduction.

structure-borne sound;wave analysis;composite wave impedance technique; blocking mass;elastic interlayer;dynamic vibration absorber

TB535 U661

A

10.3969/j.issn.1007-7294.2016.07.013

1007-7294（2016）11-1462-13

2016-05-08

工信部高技术船舶科研计划项目，工信部联装[2015]

林永水（1983-），男，博士，E-mail：peakspylin@163.com；吴卫国（19--），男，教授，博士生导师，E-mail：mailjt@163.com。