姿态显示系统的算法研究

作者/李继阳，上海交通大学电子信息与电气工程学院



姿态显示系统的算法研究

作者/李继阳，上海交通大学电子信息与电气工程学院

文章摘要：随着高性能高分辨率的微机电系统传感器的发展，越来越多的系统中采用了低能耗，高精度，高可靠性的微机电传感器。其中基于微机电传感器的姿态显示系统已经初露头角并部分程度上投入应用。更高效，更精确的的解算算法对姿态显示系统十分重要，现对姿态解算的算法进行分析。

关键词：姿态 算法

姿态的解算方法一直是人们研究的方向，现代的高科技产品需要更加精确，更加稳定，更加迅速而占用更少的计算资源的姿态解算方法。但是综合各种解算方法来看，某一方面性能的突出必然是以牺牲其他方面的性能为代价来实现的，所以在工程应用中，要考虑实际的需要，选择最适合的解算方法而并非一味追求其中的某项指标。现对几种工程上常用的姿态算法进行分析。

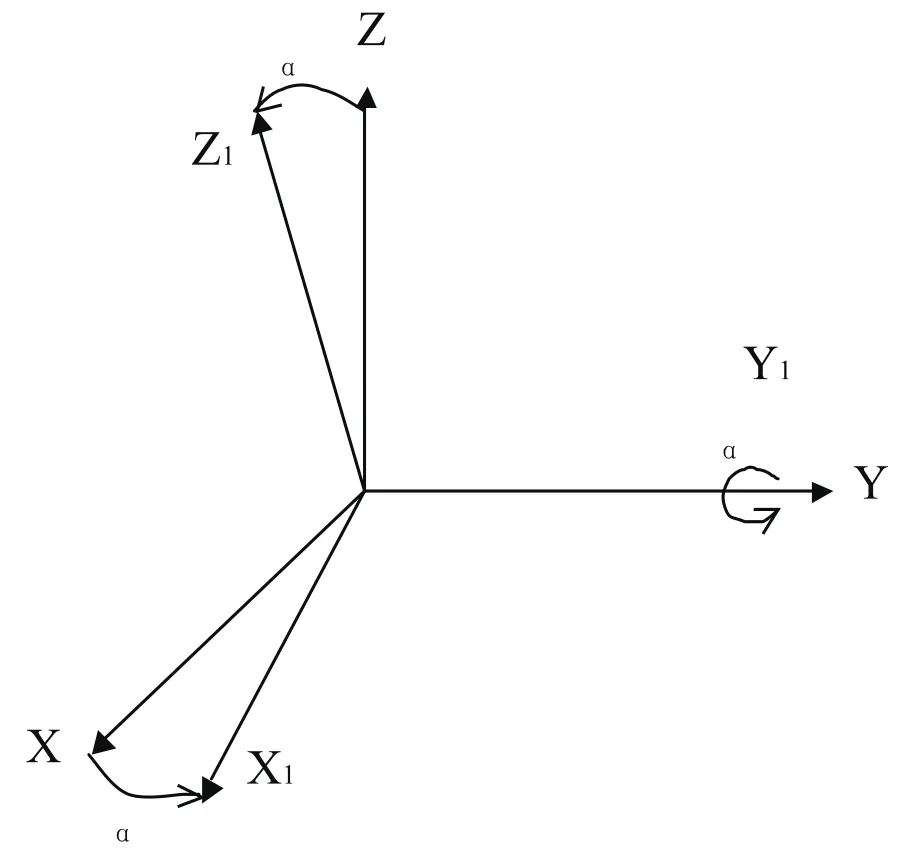
图1.1

如图1.1所示，其中XYZ坐标为地理坐标系，X1Y1Z1为机体坐标系，初始条件机体坐标系与地理坐标系重合，图示中以绕Y轴旋转α角度为例，描述了地理系与机体系之间的转换。当Y轴发生α°的正向旋转时，X轴，Z轴相应的转过α个角度，从而使机体系与地理系不重合成为X1Y1Z1。当发生绕X轴或者Z轴的旋转时，同样可以有类似的表示。这说明，机体坐标系与地理坐标系之间可以通过转换矩阵来实现两种坐标系之间的转换。而当物体发生复杂的姿态变化时，就可以转化成一系列不同的姿态转换矩阵的按次序相乘。每一次姿态的变化都可以看做物体依次绕三轴旋转了一个特定的角度，因为在绕其中一轴转动时，另外两轴都分别转过了一个角度，再次发生绕其他两轴的转动时，两轴位置已经发生了变化，所以旋转次序不同，结果也不同。姿态解算算法法的实质就是努力求出最准确的姿态转换矩阵。

1.四元数法

四元数法是工程上有着广泛应用的一种姿态解算方法，最早由爱尔兰数学家哈密顿于1843年发明，四元数法引入了新定义的虚数单位，应用范围十分广泛。在姿态解算算法中，由于四元数使得各变量之间之间有了方向性，形成姿态矩阵从而反应姿态的变化。通过四元数法可以计算出较为准确的姿态信息，其最大的好处是不占用大量的计算资源，这无疑降低了对微处理器的性能要求，从而使工程设计更易实现，同时也能节约成本，这使得四元数法在工程上得到了广泛的应用。

四元数的定义：

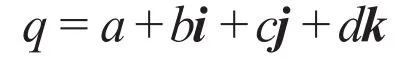
其中q是一个四元数，a b c d为实数，i j k为虚数单位，各叙述单位之间的关系如下:

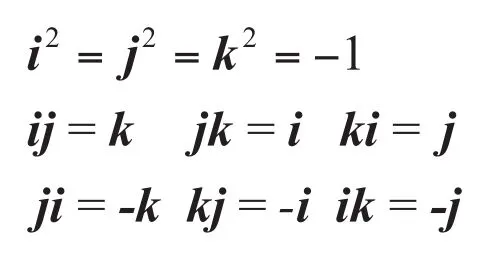
由四元数的定义可以看出，i，j，k是一种带有指向性的虚数单位，可以用来描述坐标轴的旋转，并且这种旋转是带有方向性的矢量，所以四元数之间的乘法并不满足交换律，必须按次相乘，这正好与姿态矩阵要按次相乘相对应。因此可以由四元数来表示物体姿态的变化。其中i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转，j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转，k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转，即图1.1中α的正方向。-i，-j，-k分别代表i、j、k旋转的反向旋转。

2.欧拉角法

欧拉角法可以直观的反映出姿态的变化，易于人们的理解与开发，对于要进行姿态显示的物体的俯仰角（pitch），横滚角（roll），偏航角（yaw）正好构成了一组欧拉角，这组欧拉角用来实时的反映物体的姿态信息。

欧拉角法微分关系简单，概念直观，容易理解，但是解算过程中含有三角运算，计算量大，对处理器要求高，其中的反正切运算会使俯仰角在接近90°时出现计算数据不准确的现象，所以欧拉角法只适用于水平姿态变化不大的情况[3]，不能进行全姿态的姿态解算。

3.旋转矢量法

旋转矢量法可以可以采用多子样算法以实现对误差进行有效的补偿，其算法关系 式比较简单，并且在相同的子样算法中可以通过对系数的纠正实现最小的算法漂移。旋转矢量法与四元数法都是通过四元数的计算来求得姿态更新矩阵进而反应姿态的，但两种算法的计算方式和侧重点不同，所以应用范围上也有差异。旋转矢量法通常应用于姿态角变化较为剧烈的物体姿态系统中。

4.方向余弦法

方向余弦法直接求解姿态矩阵的微分方程，可全姿态工作，不会出现死锁和方程退化的问题，但是方向余弦法对计算资源要求较高，给实时计算带来困难，不能保证姿态更新矩阵的实时性[4]。

5.三角函数法

三角函数法是目前最常用的一种综合性的姿态解算方法，其实质就是欧拉角法简化版，其忽略了地球运动对惯性坐标系造成的影响，所以三角函数法并不存在对惯性坐标系的补偿，通过集成的三角函数关系式直接解算相关姿态信息，姿态更新实时性好，应用于姿态角运动十分剧烈但位移不明显的物体姿态角的解算[5]。三角函数法部分综合了方向余弦法和四元数法，对计算资源的消耗十分严重。但是随着计算机处理器主频的增加，在计算资源足够的情况下，采用三角函数法无疑是最好的选择。

现代应用的姿态解算算法不止单纯的某一种，一般会根据其性能要求在特定的时期选择最优的解算方法。在运载火箭，运输机上一般会考虑对地球坐标系进行校正以修正其对惯性系的误差，而在小型无人机上由于位移不是很大则更多地考虑姿态对飞行器的飞行状态的影响，而究竟采取何种解算方法则要取决于具体的工程应用，在计算资源足够的情况下一般会综合各种方法进行姿态的解算以满足在某一时段对性能参数的要求。

【参考文献】

＊[1]秦永元.惯性导航［M］.北京: 科学出版社，2009.

＊[2]Ken Shoemake.Quaternions

＊[3]朱启举，秦永元，梅春波，薛媛元 基于MEMS 惯性器件的水平姿态解算方案设计，弹箭与制导学报，2013.10.

＊[4]胡佳兴，魏延辉，刘鑫，李光春.基于MEMS 的捷联姿态系统的设计与试验 创意与实践 2015.7

＊[5]郭访社，于云峰，刘书盼.捷联惯性导航系统姿态算法研究[J].航天控制，2010，28（1）.