基于建构主义下的指数函数教学研究



基于建构主义下的指数函数教学研究

◇江苏颜乾扣

构建主义学习理论认为，学生知识的获得不单是被动地接受,而是在原有知识的基础上实现自身主动构建的过程,学生依据已有的知识经验在与外部环境积极交互的过程中实现知识的增长．将其引入到数学学习和教学的过程中,就是要求学生在掌握原有知识的基础上,主动感知、消化和吸收新的数学知识,实现数学理论认知活动的构建．指数函数是基本的初等函数,在人们的日常生活、生产中有着很高的普适性,但由于数学学科本身具有抽象思维的特性,学生在刚接触到指数函数时很难理解这类数学语言的意义,所以教师在进行指数函数教学时就可以利用构建主义相关的学习理论加以指导,以帮助学生更好地理解和吸收指数函数的理论知识．

在指数函数的教学中可以利用的背景有很多,但是在情景举例之前教师要认真分析指数函数教学的现实,主要是从上行、平行和下行概念的分析入手,将指数函数的学习融入到整个数学教学的体系和过程中．上行概念包括函数的概念、图象、性质、定义域、值域、符号表达等;平行概念主要包括学生已经掌握的一次、二次、正比例和反比例函数;下行概念是本节将要学习的指数函数的性质、图象、符号表示、底数的限制等．

在背景的创设过程中教师要注意2个方面的事项:首先是要重视背景例子和学生已有知识的联系;其次要能反映出指数函数的相关概念．

情景1一种海洋生物是通过细胞的分裂来进行繁殖的：由1个会分裂成2个,然后2个分裂成4个,4个分裂成8个，……依此类推,当分裂x次之后,请问其最后的个体y与分裂次数x之间的关系如何?

情景2自然界中某种元素会随着时间而产生变化,大约每过100年就会减少为原来的1/2,假设这种元素的初始量是1,请问这种元素的含量p与经过的时间t之间有何关系?

在情景举例完成之后,教师可以让学生回答这些题目的解答过程:

生A: 情景1中的问题很简单,利用上节课的相关内容就可以知道x、y之间的关系是y=2x．

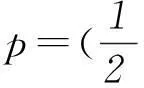
师:同学B回答的很好,但是你们对于a的取值条件有没有疑问?

生C: 我发现当a≤0的时候,y=ax没有确定的图象，所以a>0．

师:同学C回答的很好,结合一下课本中关于指数函数的图象来进行思考,还有没有人要补充?

生D: 我觉得还须考虑a和1的大小关系．因为底数与1大小的关系在指数函数单调性的研究中有着重要的影响,根据书中指数函数的图象和我刚才自己的计算可知,当a>1时,函数是增函数,且只过第一、第二象限,并且a值越小图象越无限接近x轴;当a=1时,指数函数变成直线y=1,这时候已经不能成为指数函数了;当0

师:同学D补充的非常好,结合图象我们看出a和1的大小关系对于指数函数的图象有着重要的影响,但是你们有没有发现当a>1和0

生E:老师我知道,我经过很多次的计算和观察,发现当它们对于a的取值互为倒数的时候,2个图象关于y轴对称．

师:你们回答得都很好,在你们的补充和努力下,关于指数函数的概念也越来越清晰,那么现在让我们一起来归纳总结一下:一般表示为y=ax(a>0且a≠1)的函数叫做指数函数．

在此教学过程中构建主义学习理论的相关知识得到了很好的应用．教师在教授新知识前,先选取与本堂课有关联的已经学过的知识让同学们回忆,然后在此基础上通过教学情境案例的创设将本堂课要学习的知识循循诱出,使学生在情景的提示和要求下,结合自身已有的知识主动加入到探索的过程中,总结归纳出指数函数的一般形式和注意事项．

(作者单位：江苏省兴化市文正实验学校)