基于软件节点重要性的集成测试序列生成方法

王　莹　于　海　朱志良

(东北大学软件学院　沈阳　110819)

(wangying8052@163.com)



基于软件节点重要性的集成测试序列生成方法

王莹于海朱志良

(东北大学软件学院沈阳110819)

(wangying8052@163.com)

A Class Integration Test Order Method Based on the Node Importance of Software

Wang Ying, Yu Hai, and Zhu Zhiliang

(SoftwareCollege,NortheasternUniversity,Shenyang110819)

AbstractClass integration test order is one of the most important issues in the field of software integration testing. The different integration test orders have great influence on the testing costs and testing efficiency. In order to reduce the test costs, the traditional studies of generating class-level integration test order focused on reducing the total test stub complexities and the number of test stubs. We apply the thought of “bugs should be found as early as possible” to generate the integration test order, and propose an evaluation scheme “Class-HITS” to measure the importance of software nodes. In the proposed scheme, we firstly consider the software as a network based on the complex network theory, and with the help of proposed scheme, the circles of the network are eliminated. Finally, the integration test order is obtained by reverse sorting the nodes in acyclic links. The simulations have been carried out on open-source software, which prove the efficiency of the class integration test order obtained by the proposed scheme. The new algorithm ensures the important nodes with priority to be tested, the smaller total complexity of the test stubs.

Key wordssoftware integration testing; complex network; node importance; HITS algorithm; class integration test order

摘要集成测试序列是软件集成测试的重要问题之一.不同的集成测试顺序对测试成本以及测试效率的影响很大.为降低测试成本，传统的类级集成测试顺序研究策略大多围绕如何减少构建测试桩数量和降低测试桩总体复杂度2个方面.若能将复杂程度高、出错概率大的类和发生错误后传播范围较大的类优先进行测试，不仅可以使得错误被尽早发现，还可以有效减小错误对系统的破坏性.为此，将上述思想应用到生成集成测试序列的算法当中，提出一种软件节点重要度的评估方法(Class-HITS).该方法利用复杂网络理论，将软件抽象为网络的形式，并结合所提出的重要度评估方法，打破软件网络中的环路，然后针对网络的无环链路逆向拓扑排序，最终得到类的集成测试序列.通过实验分析证明，利用该方法得出的集成测试序列既能够保证重要节点优先被测试，又确保了构造的测试桩的总复杂度较小.

关键词软件集成测试；复杂网络；节点重要性；HITS算法；类级测试序列

寻找类的测试顺序(class integration test order, CITO)是面向对象软件集成测试中重要的问题之一，类的先后测试顺序关系到错误发现的时间和构建测试桩所花费的测试成本[1].如果软件系统的类间依赖关系不存在环路，则可以通过简单的逆向拓扑排序生成集成测试序列，但事实上，软件的复杂性使得测试人员需要通过删除类间的依赖关系来进行破环操作，同时引入软件测试桩来模拟被删除边所连接的2个类之间的对象相互行为[2].

传统的类级集成测试顺序研究策略大多围绕如何减少构建测试桩的数量和降低测试桩的总体复杂度2个方面.Briand等人[3]利用遗传算法提出了生成测试顺序的方法，并基于类间的耦合度量给出了估算测试桩复杂度的公式.Le等人[4]采用基于测试依赖图模型的方法进行集成测试，在不区分边的依赖类型的情况下，减少桩的数量，但是该算法在生成测试顺序时具有不确定性，导致不同的检索方式下，构造的测试桩数目差异较大.而Tai等人[5]利用权重来选择移除能够打破最多环路的关联边，从而生成最佳测试序列.在此基础上，Briand等人[1]为继承边、聚合边和关联边赋予不同的权重，然后根据权重决定移除哪些依赖关系.姜淑娟等人[6]结合类间耦合度量与图启发式算法，在打破环路的同时保证测试桩的总复杂度尽量小.张艳梅等人[7]提出了一种基于动态依赖关系的类集成测试方法，分析了类之间的静态依赖关系和动态依赖关系，然后在保证测试桩数据尽可能小的前提下，消除环路，并开发了类测试序列的自动生成工具.上述研究在生成测试序列的同时，均未考虑软件系统中类节点的测试重要性问题，存在一定的局限性.若将易发生错误的重要测试节点排在较后位置测试，则会导致错误延迟被发现，影响软件的测试效率.因此，一组高效的集成测试序列的生成方法在软件测试研究领域具有重要的价值.

复杂性高的类引入错误的概率相对较高，应该被重点测试[8].Zhou等人[9]利用面向对象软件复杂性的度量指标对软件缺陷进行预测，研究表明软件的复杂性与软件错误的数量、分布和严重级别有着密切的关系.然而，软件缺陷在系统中并不是均匀分布的，一些简单的底层代码片段也可能出错，并且如果其在系统的多处被直接或间接调用，则会导致整个软件网络的崩溃.因此，集成测试时还应该重点考虑错误的传播影响问题[10].

本文将错误应被尽早发现的思想应用到软件集成测试序列中，利用复杂网络理论[11]，提出了一种基于软件节点重要性的集成测试序列生成方案.在集成测试前，首先对类的测试重要性进行度量，得到出错倾向性大、一旦发生错误对整个软件系统传播影响力强的类；在破环操作时，既要保证上述重要节点优先被测试，又要保证构造的测试桩总复杂度较小.

1软件重要测试节点度量方法

类的复杂性与软件缺陷呈现一定正相关性，并且在版本演化过程中，修改结构复杂性高的类比修改复杂性低的类引入错误的概率更高，可见复杂类的错误倾向性更高[12-13].此外，错误在不同的类中传播的范围以及对系统的影响力也各不相同[14-15].本文综合评估了软件中类的复杂性以及当类自身发生错误时对整个系统的影响力2个方面的因素，借鉴传统对超链接排序的HITS算法[16]思想，提出了一种复杂网络理论的节点测试重要性度量算法——Class-HITS.

1.1类级依赖网络模型

现有的针对类级测试顺序的研究大多是基于类簇之间的依赖关系形成的对象关系图(object relation diagram, ORD)，但是ORD只包含类之间的继承、关联和聚合等静态依赖关系，而事实上在软件系统中还存在着动态依赖关系.动态依赖即在程序运行期间才形成的一种依赖关系.若类Xchild继承于类Ysuper，且重写了Ysuper中的虚函数(抽象函数)，而类Zother调用了Ysuper中被重写的虚函数(抽象函数)，则在代码运行时，类Zother可能会与Ysuper的子类Xchild动态绑定，形成Zother依赖于Xchild的一条有向关系[7].

由于代码只有在运行时才能表现出软件故障与失效，这与类之间的动态依赖密切相关，只抽取静态依赖关系会造成功能路径的缺失，导致测试不充分[17].因此，本文在对软件系统进行建模时，将所有的类抽象为节点集合V={v1,v2,…,v|NC|}，节点之间的所有静态和动态依赖关系抽象为连边集合E={v1,v2|v1,v2∈V}，将软件结构表示为有向网络G(V,E)的拓扑形式，其中，NC为系统中类的总数.

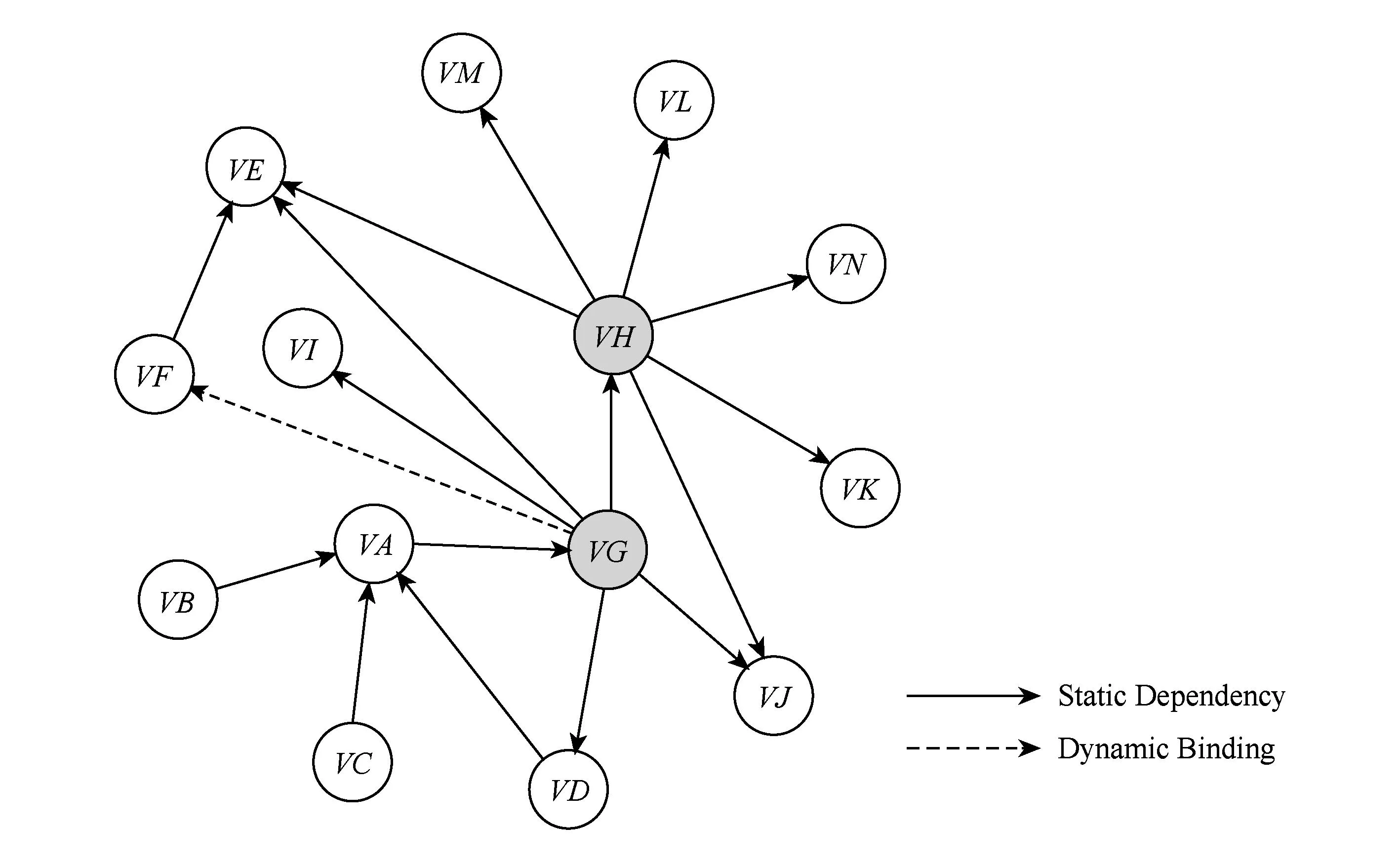
以图1(a)的代码为例，该系统由VA至VN的14个类构成，它们彼此之间存在17条依赖边，抽象出有向网络如图1(b)所示，其中，类VG与类VF之间为动态依赖关系.

classVA{VGG=newVG();inta;voidMethodA(){G.MethodG1()};}classVB{VAA=newVA();intb=A.a+1;}classVC{VAA=newVA();intc;voidMethodC(){A.a++;};}classVD{VAA=newVA();intd;voidMethodD(){A.MethodA();};}abstractclassVE{inte;abstractvoidMethodE(){};}classVFextendsclassVE{intf;voidMethodE(){f++;};}classVG{VDD=newVD();VEE=newVF();VHH=newVH();VII=newVI();VJJ=newVJ();intg=D.d;voidMethodG1(){E.e++;};voidMethodG2(){I.i++;J.j=I.i+g;};voidMethodG3(){H.MethodH2();};voidMethodG4(){I.MethodI();};voidMethodG5(){E.MethodE();};}classVH{VEE=newVE();VII=newVI();VNN=newVN();VKK=newVK();VLL=newVL();VMM=newVM();inth;voidMethodH1(){E.e++;};voidMethodH2(){I.i++;N.n=I.i+g;};voidMethodH3(){K.k=L.l+M.m;};}classVI{ inti; ︙}classVJ{ intj; ︙}classVK{ intk; ︙}classVL{ intl; ︙}classVM{ intm; ︙}classVN{ intn; ︙}

(b) The directed network of the example code

(a) The example code

Fig. 1The example code and the corresponding directed network.
图1示例代码和相应的有向网络

1.2重要测试节点的特性

显然1个类容易出错，或者一旦发生错误对系统的破坏性较大就应该优先被重点测试.因此，在分析重要节点的特征时，本文主要考虑类的影响力和类的复杂性2个方面：

1) 类的影响力(impact of class, IC)通常在分析面向对象软件中类的传播影响力时，都是用节点的入度值来衡量，即如果1个类被越多的类所直接依赖，则当该类发生错误时对软件系统的影响力越大.但是仅仅以入度值来评估类的影响力具有片面性，忽略了依赖这个类的其他类的复杂程度.类越复杂，其越有可能是网络中的“Hub”节点，与之存在耦合关系的类可能越多，其自身承担的功能也可能会越强大[11].如果1个类被多个复杂的类所依赖，则当这个类出错时，可能会导致网络的“涟漪效应”，从而造成错误的波及范围变大，这样的类应该优先被重点测试[18].图1(a)所示，节点VA和VE入度同为3，在网络中具有一定的传播影响力，区别在于节点VA只是被3个复杂性较低的VB，VC，VD所调用，而调用节点VE的类中包含复杂性高、功能强大的VG和VH，所以当VE发生错误时就可能会传播到VF，VG，VH，VA，VD等距离更远的节点，导致不能顺利运行的功能路径更多，且影响的功能也会更加重要.

2) 类的复杂性(complexity of class, CC)研究表明类的复杂性与面向对象软件类的错误倾向性具有密切联系，且大多使用C&K等复杂性度量指标来衡量[19-20].却忽略了该类依赖的其他类的传播影响力和结构复杂性，如果1个类依赖了越多错误传播性强、影响力大的类，那么由于耦合关系将错误间接传递到该类自身的倾向性就会越大，其测试重要性和优先级也就越高.例如图1(b)中，节点VG和VH的出度同为6，为网络中的“Hub”节点，具有一定的枢纽性，且较为复杂的节点，但是VG调用了VH的函数MethodH2()，而VH的函数MethodH2()又调用了VI和VN的属性，导致VH的复杂性和传播影响力直接或间接地传递到了VG中，所以VG的错误倾向性实质上高于VH.

由此可见，类的复杂性和错误传播影响力相互作用、相互影响.类的复杂性与该类依赖的其他类的错误传播影响力相关，而类的错误传播影响力与所有依赖该类的其他类的结构复杂性相关.

1.3Class-HITS算法描述

通过分析可以发现，上述重要测试节点的2个特性：影响力和复杂性与计算超链接重要性的HITS算法思想中刻画网页重要性的2个指标——权威值和枢纽值极为相似.在HITS算法中，权威值受入度因素影响，而枢纽值受出度因素影响.一般地1个页面的权威值由指向该页面的其他页面的枢纽值来决定：如果1个页面被多个具有高枢纽值的页面所指向，那么该页面就具有较高的权威值.另一方面，1个页面的枢纽值，由它所指向的页面的权威值来刻画：如果1个页面指向多个具有高权威值的页面，那么该页面就具有高枢纽值[16,20-21].将上述理论中的页面权威值和枢纽值分别使用类的复杂性和传播影响力来替换，同样可以适用于软件测试节点重要性的计算.本文对HITS算法进行修改，提出了一种基于复杂网络的节点重要性度量算法Class-HITS：

1) 将网络G(V,E)中任意类节点vi∈V，1≤i≤|V|的复杂性和影响力的初始值设置为该类自身的复杂性度量值Ci.类自身的复杂性由多种因素共同决定，研究表明，类的规模、耦合性和结构复杂性是最重要的3个方面[8-9]，而C&K度量套件中的上述指标也经常被用来预测类的错误倾向性[12-13,19-20].本文类的规模使用代码行数和特征总数来度量，特征总数为类中所有属性和方法数目的总和，耦合性用与该类存在耦合关系的类的数目来描述，结构复杂性表示为类中所有方法的圈复杂度之和[22]，最后，求出4种度量值归一化后结果的加权之和即为初值Ci，如式(1)所示.这里令α+β+ω+δ=1，α，β，ω，δ∈，1≤i≤NC，WMCi，CBOi，LOCi，NOFi分别为类vi的结构复杂性、耦合度、代码行数、特征总数值.

(1)

2) 由于类并不是软件中最基本的元素，那么在有向类级软件网络中，节点之间的连边表示的也并不是2个类之间100%的依赖关系.若用call(i,j)表示节点vi依赖类节点vj的特征数目，NOFj表示vj中所有属性和方法数目的总和，则vi与vj的依赖比例值γij定义为

(2)

3) 节点测试重要性Wi的计算要综合考虑该类vi的传播影响力ICi和错误倾向性CCi.如式(3)所示，取二者的加权之和，即：

(3)

经过上述改动的目的是：1)将类自身的复杂性融入到类的传播影响力和复杂性的迭代计算中，使得类的复杂性不仅与该类自身的结构复杂性相关，而且与该类依赖的其他类的复杂性和传播影响力相关，随着迭代次数的增加，通过与该类的直接或间接依赖关系以一定概率γ累加到该类复杂性CCi的计算中；2)类的传播影响力不仅与直接或间接调用这个类的其他类的个数相关，也与这些类的复杂性相关，该类被越多结构复杂性和错误倾向性高的类所依赖，则这个类发生错误时，错误通过与该类直接或间接的依赖关系以概率γ影响到的类以及功能路径的范围就越广，影响到的系统功能也可能越重要.Class-HITS算法表述如下：

算法1. Class-HITS.

输入：类级有向软件网络邻接矩阵A=(aij)NC×NC；

输出：节点测试重要性向量W=(W1,W2,…,WNC).

步骤1. 设定网络中每个节点的影响力和复杂性初始值皆为类自身复杂性Ci的值, x(0)=(C1,C2, …,CNC)T,y(0)=(C1,C2,…,CNC)T.

步骤2. 节点影响力和复杂性向量的校正.节点的影响力和复杂性向量重复执行步骤2.1～2.3的k次迭代，直到2组向量趋于稳定，退出迭代.这里假设2组向量趋于稳定的条件是‖xi(k)-xi(k-1)‖+‖yi(k)-yi(k-1)‖<ε.

步骤2.1. 节点影响力校正规则：每一个类节点的影响力校正为指向它的节点的复杂性乘以这2个节点间的依赖比例所得结果之和，即:

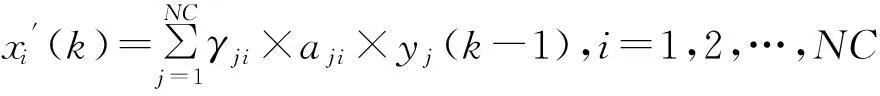
当且仅当有1条从节点vi指向节点vj的有向边，aij=1，否则aij=0.

步骤2.2. 节点复杂性校正规则：每一个类节点的复杂性校正为它所指向的节点的影响力乘以这2个节点间的依赖比例所得结果之和，即

步骤2.3. 归一化：

步骤3. 令W=0.5×x(k)+0.5×y(k)，输出W.

同样以图1(b)所示的软件网络为例，加权邻接矩阵A′和类的影响力及其复杂性的初始向量x(0)和y(0)如下，由于缺乏详细信息，初始向量中的Ci值只用耦合度CBOi和特征数NOFi这2种度量指标，经历大约10次迭代后，2组向量趋于稳定，从而得出最终的影响力和复杂性的结果向量如向量x(k)，y(k)，W所示，其中A表示类节点VA至VN的邻接矩阵：

节点VG和VH的CC值分别为1.846 2，1.321 4，VG的复杂性大于VH，节点VA和节点VE的IC值分别为0.179 0，0.473 3，VA的传播影响力小于VE.综合来看，节点测试重要性排名前3的分别为VG，VH，VF3个节点，分别具有较高的错误倾向性和传播影响力，且VG的CC值高于VH，应当被重点测试.综上，通过Class-HITS计算出的节点测试重要性值，与上文的分析结果一致.

2集成测试序列生成方法

通过1.2节分析，在软件系统中错误倾向性较高和传播影响力较大的类，对软件的稳定性起着决定性作用[10,15]，因此本文综合考虑重要测试节点优先和降低测试桩复杂度2个因素，给出一种生成集成测试序列的算法，在保证错误尽早发现的同时，又缩减了测试成本.

2.1测试桩复杂度度量

测试桩，即用来开发或者测试一个依赖桩的组件，它是软件模块的一种概括或者基于某种特殊目的的实现[6,12].假设类VA依赖类VB，集成测试时，如果当测试类VA时，类VB尚未被测试，此时就需要为类VA模拟一个类VB的对象，这个模拟出来的Stub(VA,VB)就是测试桩，测试桩可以为待测类提供调用的属性和方法[1].但是，在面向对象软件系统中，模拟一个对象构造测试桩的代价很大.因此，在集成测试时，要尽量减少测试桩的复杂度以及避免给过于复杂的类模拟测试桩[3].

构建测试桩的代价可以用桩复杂度来估算.本文测量桩复杂度的方法利用文献[3]的公式：

(4)

2.2集成测试顺序

生成集成测试序列的目标是类级测试顺序要最大程度地保证在每一个类测试之前，它所依赖的类都已经测试完毕，即沿着类的依赖关系方向逆向排序，这样既可以减少测试桩的数目，同时确保了集成测试的完整性[7,23].由此，可利用软件网络拓扑结构，找出类间关系构成的所有环路，随之通过删除连边对软件网络进行破环操作，使其从有环图转为无环图，这里每删除1条边，就需要为其建立1个测试桩，即删除边数等于测试桩数目.在不存在环路的情况下，类的测试顺序很容易根据依赖关系逆向排列.

本文在执行破环操作时要同时达到2个目标：既要满足错误倾向性高、传播影响力大的节点被优先测试，又要满足构造的测试桩总复杂度较低.

定义1. 依赖路径PathD.假设SV为网络中所有入度为0且出度不为0的类节点集合，EV为网络中所有出度为0且入度不为0的节点集合，若有任意类节点vs∈SV，ve∈EV，且其之间可达，则称PathD为一条vs与ve之间的依赖路径.

定义2. 依赖深度D.设类节点vs∈SV，ve∈EV，若vs到ve存在一条依赖路径PathD={v1,v2,…,vk,vk+1,…,vn}，则节点vk的依赖深度满足Dk=|n-k|+1.

若Wi表示有向环路边vi,vj起始节点vi的重要度值，Wi为Wi归一化后的结果，，其中，Wmin和Wmax分别表示表示当前网络中所有边的Wi最小值和最大值，Loops(i,j)表示包含边vi,vj在内的环路总数，Loops′为Loops(i,j)归一化后的结果，，Loopsmin和Loopsmax分别表示表示当前网络中所有边的Loops(i,j)最小值和最大值，SCplx(i,j)表示如果删除了边vi,vj后，需要为节点vi构建的节点vj的测试桩复杂度，则提出测试优先度We(i,j)的定义如下：

定义4. 测试优先度We(i,j)表示为构成环路的边vi,vj赋予的权值，vi和vj分别为连接环路边vi,vj2端的一类节点，1≤i,j≤NC,则有：

(5)

We(i,j)的含义是不但要保证重要度较高的节点vi可以优先被测试，且删除边vi,vj的同时打破的环路数较多，即确保构造的测试桩数目较低，更要使得构造的测试桩复杂度SCplx(i,j)较小.测试优先度为本文算法的核心思想，按照测试优先度值的高低选择将要删除的边vi,vj，并为该边vi,vj构造测试桩，同时，本文也以We(i,j)作为破环优劣的评价指标，生成集成测试序列的步骤如下：

1) 使用Tarjan算法深度优先遍历类级有向网络G中的每一个节点，寻找到G中的每一个强连通分量SCC,由强连通分量的定义可知，有向图的环路一定存在于SCC中.

2) 依次遍历每一个SCC，在每个SCC中查找环路，接下来遍历每一个环路，然后将每个环路中的每条边按照式(5)赋予边权值.

3) 删边操作，在删除边时，遵循4个原则：

① 当环路中边权值最大的边只有一条时，删除环路中边权值最高的边；

② 如果边权值最大的边不止一条，则计算环路中所有边终止节点的测试桩复杂度，选择测试桩复杂度最小的边删除；

③ 如果边权值最大的边不止一条，且这几条边终止节点的测试桩复杂度也相等，那么删除任意一条以重要度值最大的节点为起始节点的边；

④ 直到有向图中再无环路时，删边结束.

4) 过滤掉无环网络的孤立节点，并对其剩余节点依次遍历，计算每个节点的最大依赖深度Dmax，对Dmax相同的节点按照节点的重要度值Wi降序排序，对Dmax不同的节点按照节点的Dmax值升序排序.

5) 软件网络中的孤立节点大多是为后续功能扩展而预留的接口，故随机排在最后，由此得到的节点顺序即为最后总的集成测试序列O，O为有序集合.

对软件源代码扫描过后，将节点重要度评估的Class-HITS算法与网络逆向拓扑排序相结合，得出最终结果.生成类级集成测试序列的算法如图2所示:

Fig. 2　The diagram of generating integration test order algorithm.图2　本文生成集成测试序列算法示意图

3实验分析

本文采用DNS 1.2.0①，ANT 1.9.4②，BCEL 5.0③这3款软件作为实验数据来验证本文算法的有效性.选择这3个系统的原因是:包括文献[1,3,6-7]在内的多个软件集成测试实证研究中，这DNS，ANT，BCEL均被用作实验测试对象.这3个系统的类数目从25～61不等，环路数目从16～416 091差异较大，因此可以从不同规模、复杂性以及环路密度等角度来共同验证集成测试算法.类的序号顺序与上述文献的顺序完全一致，在文献[3]的附录已经详细列出.

3.1重要测试节点实验分析

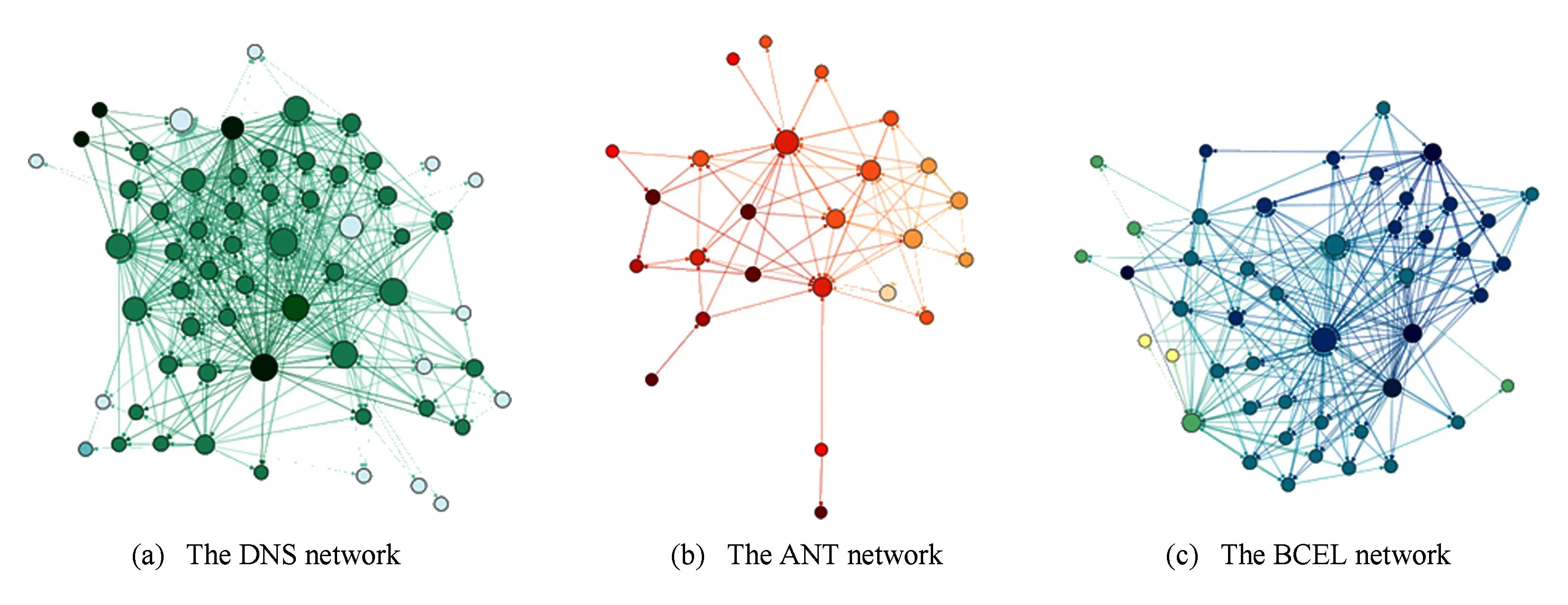
Fig. 3　The software networks obtained by the dependency finder.图3 Dependency Finder 抽象出的软件网络

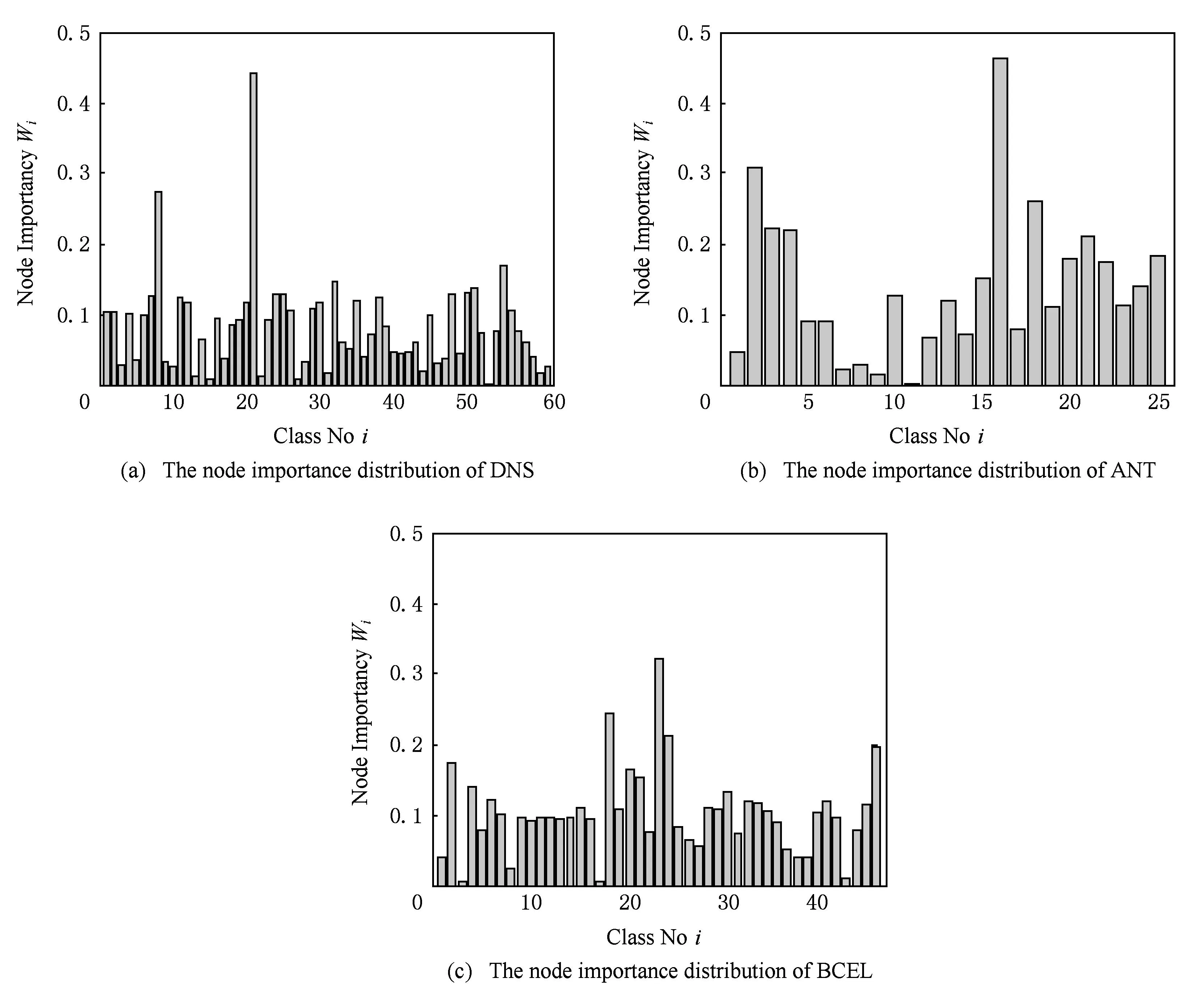
Fig. 4　The node importance distribution diagram.图4　节点重要度值分布图

SoftwareNnodeWmaxWminWICmaxICminICCCmaxCCminCCDNS610.44210.00150.08270.702400.06730.262100.0982ANT250.46310.00070.13920.489300.14440.632000.1341BCEL450.32150.00640.10330.328600.12690.643000.0797

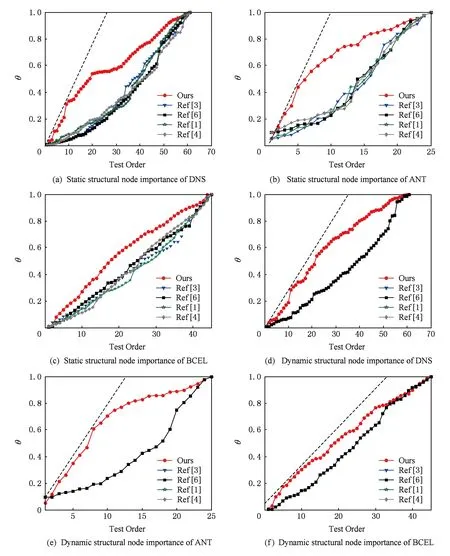
Fig. 5　The comparison of the node importance in the test order.图5　测试序列节点重要度情况对比

如表2所示，分别为重要度值排名前5和后5的类节点结构度量值，本文分别使用节点的入度Kin、特征被调用次数Pce、出度Kout、特征总数NOF、调用特征次数Pc、结构复杂性WMC、代码规模LOC表征类在系统中的重要程度，这些指标皆与本文提出的节点影响力、复杂性和节点重要度值成一定正相关性.在软件DNS中，重要度值排名第1的21号类节点org.xbill.DNS.Name，内部含有33个特征，拥有系统最大的入度值，被除自身以外的其他40个类调用了135次，调用其他5个类的特征48次，虽然其特征被调用次数小于重要度值排名第2的8号类org.xbill.DNS.Compression，但是由于直接或间接调用21号类的其他类的结构复杂性和错误倾向性较高，导致它具有较高的影响力.软件ANT重要度值最大的是16号类org.apache.tools.ant.Project，内部含有131个特征，其结构复杂性(WMC值)、代码规模(LOC值)、入度值、特征被调用次数、和调用次数分别是37，2300，14，125，98，而这些指标皆为系统中最高值.软件BCEL中，重要度值排名第1的为第23号类节点org.apache.bcel.classfile.DescendingVisitor，虽然它的入度值为0，但是其拥有最大的出度值、结构复杂性(WMC值)和码规模(LOC值)，平均每个特征调用其他类的特征4.4次，也就是说，其他类的错误倾向性和结构复杂性随着依赖关系大大加重了23号类的复杂性，这些类一旦发生错误也极易传播进23号类中.排名靠前的其他节点与表格列出节点类似，均具有较高的入度、出度、被调用次数或者调用其他类特征次数，相应地也就拥有较高的复杂性因子或者影响力因子，应该被尽早测试.在排名后5的节点中，很多节点的入度值或出度值为0，缺乏由于直接或间接调用其他类的特征而产生的复杂性，以及直接或间接被其他类的特征调用而产生的传播影响力.与系统中其他类相比，较为简单且出错概率小，且一旦出错也不会传播到软件系统的其他类中，对于这样的类，测试的优先级理应靠后.综上，本文提出的针对软件网络节点测试重要性评估的Class-HITS算法正确有效，排序结果也可以应用到后续的生成集成测试序列中.

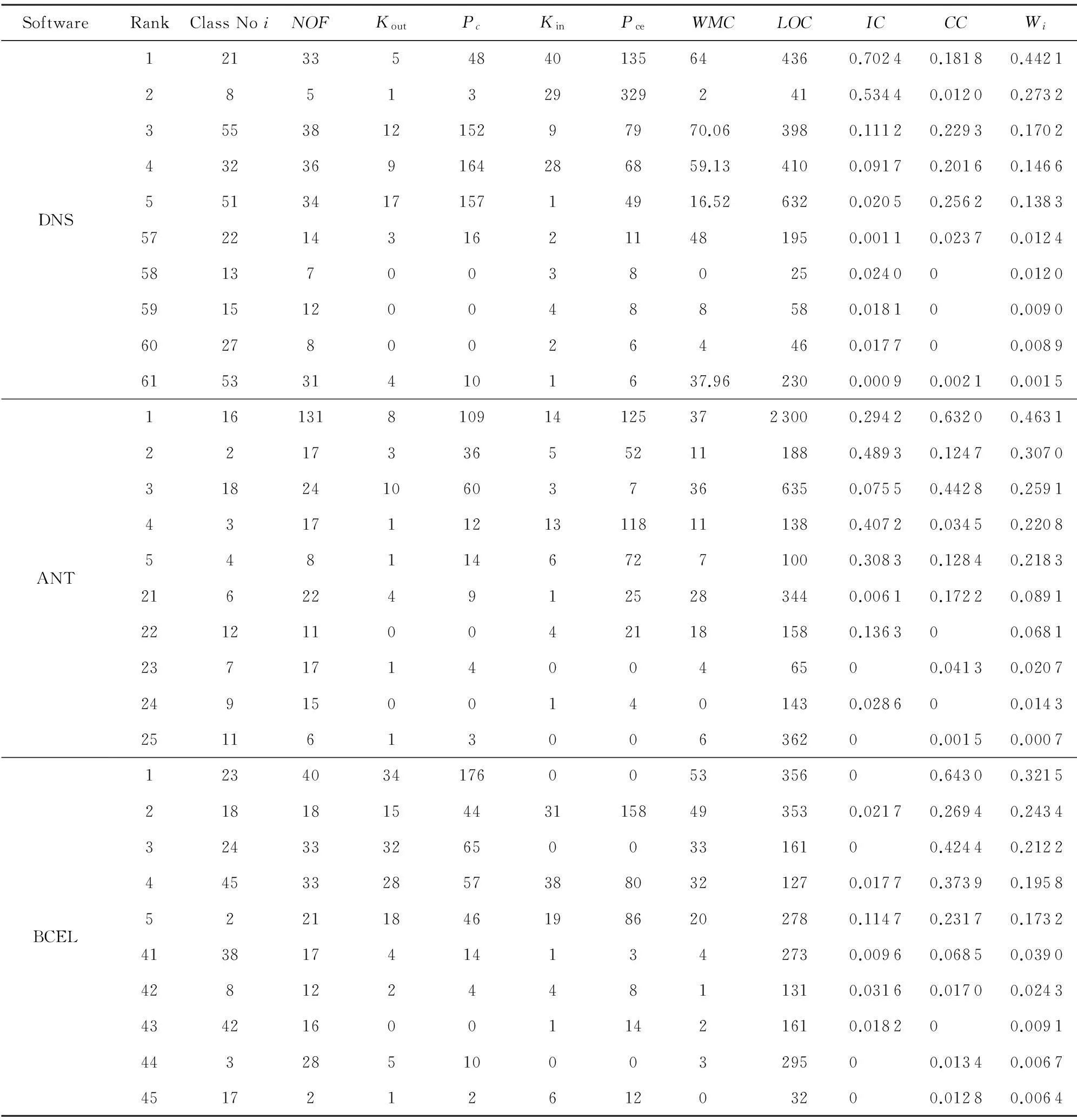
Table 2　The Statistic of the Top Five Nodes And Last Five Nodes

3.2生成集成测试序

得到软件网络所有节点的测试重要度值后，再根据2.2节提出的方法，求出3种软件的集成测试序列，并与文献[1,3-4,6-7]进行对比分析.其中，文献[1,3-4,6]的系统模型只考虑了类间静态依赖关系，而文献[7]加入了动态依赖的分析.为了保证对比的公平性，本文分为2种情况讨论，首先忽略掉动态依赖边，与前4种算法比较，然后加入动态依赖边与文献[7]进行对比分析.此外，文献[1,4,7]算法得到的测试序列均是以减少测试桩数目为前提；而文献[3,6]是以降低测试桩的总复杂度为目的.这里，测试优先度的计算式(5)中η，μ的值皆暂取为0.5.为方便对照，本文类的序号顺序、测试桩复杂度的公式均与文献[3,7]相同，即λ=τ=0.5.

首先，使用Tarjan算法在网络中查找强连通分量SSC，然后进行破环操作.软件DNS在加入动态依赖边的同时，并没有增加网络的环路个数.所以，在2种情况下，系统内均包含2个强连通分量，分别为{33,38,52}以及{58,48,32,25,11,8,21}，共形成了16个环路，在静态依赖结构下，应用本文算法与文献[3]在破环的过程中均删除了6条边{21→11,21→8,32→48,32→58,38→33,52→33}，需要建立的测试桩总复杂度为1.47，均低于文献[1,4]，相应地在建立测试桩的同时，平均能够比文献[4]少建立39个属性和71个方法.而在加入动态依赖的模型中，本文的测试桩总复杂度与文献[7]相同.

在静态依赖结构下，软件ANT中包含1个强连通分量，其内部含有12个节点{4，22，23，19，21，10，18，20，17，16，24}，形成654个环路.虽然文献[1,3,6]分别删除了11，12和10条就破除了所有环路，而本文在破环过程中共删除了18条边，但是应用本文算法所建立的桩总复杂度分别比文献[1,3-4,6]的结果少了0.03，0.31，0.44，0.02.文献[1,3-4,6]在建立测试桩的同时需要为所有的测试桩模拟属性和方法总和分别为175.5，367.7，205，172，而本文构造测试桩的属性和方法总和仅为147，节约了测试开销.加入动态依赖的20条边后，软件ANT系统内的强连通分量为{1,16,2,4,5,10,18,19,20,21,22,23,24,25,17}，环路数增加至8 894，在生成测试序列时文献[7]共删除了23条边，而本文删除了30条.但是，本文算法建立的桩总复杂度较低，且建立桩的方法和属性综合相比文献[7]少了140个.

静态结构下的软件BCEL中包含1个强连通分量，其内部含有40个节点.也就是说，网络中除节点1，3，23，24，42外，皆构成强连通分量，虽然该软件网络节点总数较低，但却形成了416 091个环路，文献[1,3-4,6]在破环过程中平均删除70，67.5，71，73条边，而本文删除的边数为94，虽然删边数较多，但是建立的桩总复杂度较文献[3-4,6]分别降低了2.36，1.93，0.53，本文为所有的测试桩模拟属性和方法总和与文献[3-4,6]相比，分别少了177，115，54.而增加了138条动态依赖边后，BCEL的环路数目变为626 826个，本文需要删除96条边才能够打破所有环路，而文献[7]的算法只建立了87个测试桩，但是，本文的测试桩总复杂度较文献[7]减少了0.98，需要模拟的属性和方法总数比文献[7]减少了106个，大大降低了测试成本.

Table 3　The Test Orders Obtained by the Proposed Algorithm

表4中NUMp表示当测试完节点总数50%的时候，重要度排名前30%的节点就已经被测试完毕的数目.3组实验中利用本文算法得出的NUMp值均大于文献[1,3-4,6-7]的结果，并且这种优势随着软件网络节点数的增加而增大，例如在静态结构下，具有25个节点的软件ANT，本文算法与文献[1,3-4,6]的NUMp的差值分别为3，2，2，3.加入动态依赖关系后，本文算法与文献[7]得到的NUMp差值是3.静态结构下具有45个节点的BCEL软件，本文算法与文献[1,3-4,6]NUMp的差值为6，7，6，6.加入动态依赖关系后，本文与文献[7]的NUMp差值是3.静态结构下，具有61个节点的DNS软件，本文算法与文献[1,3-4,6]的NUMp的差值最大，分别为9，8，7，8.加入动态依赖关系后，本文与文献[7]的NUMp差值是6.

利用3种算法生成的测试序列，其节点重要度的统计情况如图5所示，横坐标代表不同算法的测试序列O，纵坐标代表已完成测试节点的重要度累加和所占全部节点重要度总和的百分比(图5(a)～(c)和图5(d)～(f)分别表示静态结构和动态结构下3个软件系统重要度值的统计结果.从图5中可以观察出，由本文算法得出的测试序列，无论是静态依赖网络模型还是加入动态依赖关系后的网络模型，在整个集成测试过程的前半部分，其测试节点的重要度累加曲线变化率明显大于文献[1,3-4,6-7]，即对相对重要的节点进行了优先测试.

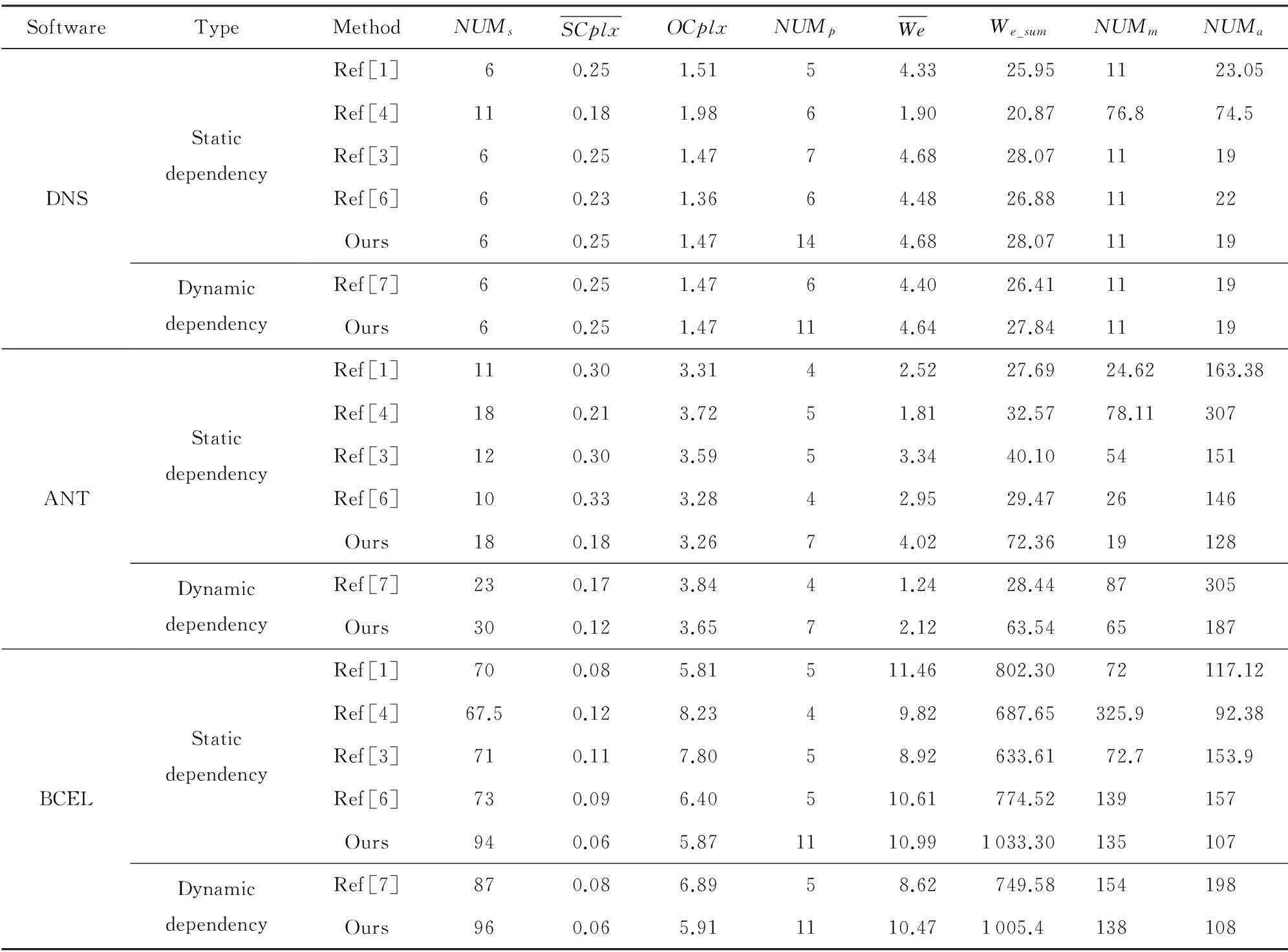
Table 4　The Comparison of the Experiment Results

由于本文使用测试优先度We(i,j)为每一条边赋予权值，然后按照权值的高低排序来选择将要删除的边，从而进行破环操作.如果单纯将结构复杂的类优先测试，由于其出度较大，可能会引起测试桩复杂度的激增，但是本文的节点重要度由类的错误倾向性和传播影响力2个因素构成，其中，类的错误倾向性虽然与类的出度因素相关，同时也受该节点的耦合度，结构复杂性，特征总数和代码规模等指标以及它所指向的其他类的传播影响力和结构复杂性等多种因素影响.并且We(i,j)除了由节点重要度条件决定以外，还与桩复杂度和测试桩数目等因素相关.综合上述实验结果可以得出结论，由本文算法生成的测试序列，不仅重要的类节点被优先测试，且可以保证测试桩复杂度较小，提高测试效率的同时，节约了测试成本.

4结论

本文将软件系统中重要测试节点的2个特性——类的复杂性和类的影响力——结合起来，提出一种新的针对软件网络节点测试重要性评估的Class-HITS算法.从而将系统中容易出错的类，以及发生错误后波及范围较大的类视为重要测试节点.以尽早发现软件缺陷和有效控制错误的传播范围作为测试目标，结合上述Class-HITS算法打破网络中的环路，生成类级集成测试序列.通过与现有算法的实验对比分析，证明了本文算法生成的类级集成测试序列，既保证了重要度值高的节点优先被测试，又降低了构造的测试桩总复杂度，减少测试代价，可被应用于软件集成测试领域中.

参考文献

[1]Briand L C, Yvan L, Wang Yihong. An investigation of graph-based class integration test order strategies[J]. IEEE Trans on Software Engineering, 2003, 29(7): 594-607

[2]Kung D C, Gao J, Hsia P. On regression testing of object-oriented programs[J]. Journal of Systems and Software, 1996, 32(1): 21-40

[3]Briand L C, Feng J, Labiche Y. Experimenting with genetic algorithms to devise optimal integration test orders[J]. Software Engineering with Computational Intelligence, 2003, 73: 204-234

[4]Le T Y，Jéron T，Jézéquel J. Efficient object-oriented integration and regression testing[J]. IEEE Trans on Reliability, 2000, 49(1)：12-25

[5]Tai K C, Daniels F J. Interclass test order for object-oriented software[J]. Object-Oriented Programming, 1999, 12(4): 18-25

[6]Jiang Shujuan, Zhang Yanmei, Li Haiyang, et al. An approach for inter-class integration test order determination based on coupling measures[J]. Chinese Journal of Computers, 2011, 34(6): 1062-1074 (in Chinese)(姜淑娟, 张艳梅, 李海洋, 等. 一种基于耦合度量的类间集成测试序的确定方法[J]. 计算机学报, 2011, 34(6): 1062-1074)

[7]Zhang Yanmei, Jiang Shujuan, Zhang Hongchang. An approach for class integration testing based on dynamic dependency relations[J]. Chinese Journal of Computers, 2011, 34(6): 1075-1089 (in Chinese)(张艳梅, 姜淑娟, 张红昌. 一种基于动态依赖关系的类集成测试方法[J]. 计算机学报, 2011, 34(6): 1075-1089)

[8]Munson J C M, Khoshgoftaar T M. The detection of fault-prone programs[J]. IEEE Trans on Software Engineering, 1992, 18(5): 423-433

[9]Zhou Yuming, Hareton L. Empirical analysis of object-oriented design metrics for predicting high and low severity faults[J]. IEEE Trans on Software Engineering, 2006, 32(10): 771-789

[10]Pan Weifeng, Li Bing, Ma Yutao, et al. Test case prioritization based on complex software networks[J]. Acta Electronica Sinica, 2012, 40(12): 2456-2465 (in Chinese)(潘伟丰, 李兵, 马于涛, 等. 基于复杂软件网络的回归测试用例优先排序[J]. 电子学报, 2012, 40(12): 2456-2465)

[11]Myers C R. Software systems as complex networks：Structure, function, and evolvability of software collaboration graphs[J]. Physical Review E, 2003, 68(4): 046116

[12]Zhou Yuming, Xu Baowe, Hareton L. On the ability of complexity metrics to predict fault-prone classes in object-oriented systems[J]. Journal of Systems and Software, 2010, 83(4): 660-674

[13]Zhou Yuming, Xu Baowe, Hareton L, et al. An in-depth study of the potentially confounding effect of class size in fault prediction[J]. ACM Trans on Software Engineering and Methodology, 2014, 23(1): 1-51

[14]Damien C, Andrea L. Bug propagation and debugging in asymmetric software structures[J]. Physical Review E, 2004, 70(4): 046109

[15]Jing Liu, Lu Jinhu, He Keqing, et al. Characterizing the structural quality of general complex software networks[J]. International Journal of Bifurcation and Chaos, 2008, 18(2): 605-613

[16]Kleinberg J. Authoritative sources in a hyperlinked environment[J]. Journal of the ACM, 1999, 46(5): 604-632

[17]Xie Bing, Zhang Chendong. A test script generating method and tool for OO test model[J]. Journal of Computer Research and Development, 2008, 45(Supp1): 336-340 (in Chinese)(谢冰, 张晨东. 一种基于面向对象测试模型的测试代码生成方法与工具[J]. 计算机研究与发展, 2008, 45(增刊): 336-340)

[18]Potanin A, Noble J, Frean M. Scale-free geometry in object-oriented software programs[J]. Communications of the ACM, 2005, 48(5): 99-103

[19]Ramanath S, Krishnan M. Empirical analysis of CK metrics for object-oriented design complexity: Implication for software defects[J]. IEEE Trans on Software Engineering, 2003, 29(4): 297-310

[20]Hector M O, Letha H E, Sherri L M, et al. An empirical validation of object-oriented class complexity to predict error-prone classes in highly iterative, or agile, software: A case study[J]. Journal of Software Maintenance and Evolution: Research and Practice, 2008, 20(3): 171-197

[21]Wang Xiaofan, Li Xiang, Chen Guanrong. Network Science: An Introduction[M]. Beijing: Higher Education Press, 2012: 158-176 (in Chinese)(汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012, 158-176)

[22]McCabe T. A complexity measure[J]. IEEE Trans on Software Engineering, 1976, 2(4): 308-320

[23]Abdurazik A, Offutt A J. Using coupling-based weights for the class integration and test order problem[J]. The Computer Journal, 2009, 52(5): 557-570

Wang Ying, born in 1987. PhD candidate. Her main research interests include software refactoring, complex networks, software networks and software testing.

Yu Hai, born in 1971. PhD, associate professor. His research interests include software refactoring, software testing, multimedia security and secure chaos-based communications, information hiding, video coding, digital chaotic cipher, network coding, channel coding and applications of complex-network theories.

Zhu Zhiliang, born in 1962. PhD, professor and PhD supervisor. His main research interests include information integrate, complexity software system, network coding and communication security, chaos-baseddigital communications, applications of complex-network theories and cryptography (zzl@mail.neu.edu.cn).

中图法分类号TP311.5

通信作者：于海(yuhai@mail.neu.edu.cn)

基金项目：国家自然科学基金项目(61374178，61402092)

收稿日期：2014-12-05；修回日期：2015-07-21

This work was supported by the National Natural Science Foundation of China (61374178，61402092).