基于局部二值拟合模型的板材表面节子与虫眼的图像分割

白雪冰，许景涛，郭景秋，陈　凯（东北林业大学机电工程学院，黑龙江哈尔滨150040）



基于局部二值拟合模型的板材表面节子与虫眼的图像分割

白雪冰，许景涛，郭景秋，陈凯
（东北林业大学机电工程学院，黑龙江哈尔滨150040）

摘要：为了更好地对板材表面的节子和虫眼进行快速有效的分割，对局部二值拟合（local binary fitting，LBF）模型进行了深入研究，从而提出一个改进的LBF模型，即在LBF模型的基础上，添加一个新的水平集线性正则化项，与此同时引入一个以高斯函数为核函数的局部二值拟合能量。改进算法能够克服LBF模型的分割缺点，使得分割过程对初始轮廓的大小和位置不敏感，同时增强算法的抗噪性，能够分割出灰度不均匀的图像。经实验验证，该算法可以比较完整地提取出单一目标和多目标的板材节子和虫眼的图像，以及对应得出与缺陷图像相对应的水平集演化图像。图21表1参15

关键词：木材科学与技术；板材表面缺陷；板材图像分割；LBF模型；水平集

20世纪90年代，德国应用超声波技术得到木材超声波图像，通过对图像分析来检测木材缺陷。美国等发达国家研制了超声波木材检测仪，该方法可以快速简便地检测出木材缺陷，但需要借助中间均匀介质（如水或油等），难以实现连续性检测［1］。法国已研制出微波木材检测仪，但检测结果受到木材含水率高低影响较大，该方法的适用范围和精确度还需要不断提高。加拿大、澳大利亚等国家将X射线扫描技术应用到木材检测中，该方法对木材常见缺陷检测较为有效，但是检测设备不但造价高而且防护措施比较苛刻［1-2］。中国的木材缺陷检测技术主要还是以人工检测为主，在生产过程中由于劳动强度较大，个人检测经验和主观认知不同，检测效率和准确率都较低，难以实现自动化要求。近年来，几何活动轮廓模型得到国内外学者的广泛关注，成为图像分割的主流方法之一［3-4］。其中，几何活动轮廓模型基于曲线演化和水平集的方法备受瞩目，即水平集函数在一个偏微分方程的控制下进行演化［5］，直到零水平集演化到图像的目标边缘为止，从而得到目标轮廓［6］。CV（chan-vese）模型是一个基于区域的几何活动轮廓模型［7］，由于CV模型不能分割灰度不均匀图像［8］，因此，LI等［9］于2008年提出了RSF（region-scalable fitting）模型，又称局部二值拟合（local binary fitting，LFB）模型。该模型把CV模型的全局二值拟合能量泛函改为以高斯函数为核函数的可变区域拟合能量定义的能量泛函［10］，从而较好地克服了CV模型的缺点，能够分割出灰度不均匀图像［11］。LBF模型以考虑局部均值信息为主要分割方式，对于边界灰度较弱的图像分割困难，演化速度较慢，分割时依赖于演化曲线以及初始轮廓的位置，而且受噪声影响较大。为了克服LBF模型的缺点，本研究在LBF基础上添加一个新的水平集线性正则化项，同时提出了一个新的核函数与LBF模型相结合的算法对板材表面缺陷进行分割，从而使得该算法不仅能够分割灰度不均匀的图像，而且对初始轮廓的大小和位置不敏感，同时增强模型的抗噪性［12］。

1　LBF模型介绍

1.1LBF模型水平集改进模型

LBF模型是基于一种可变区域的的能量泛函模型，设Ω⊂R2为整个图像的空域, I∶Ω→R映射为灰度级图像，针对图像空域Ω中的一点x和初始轮廓曲线c。LBF模型能量定义为：

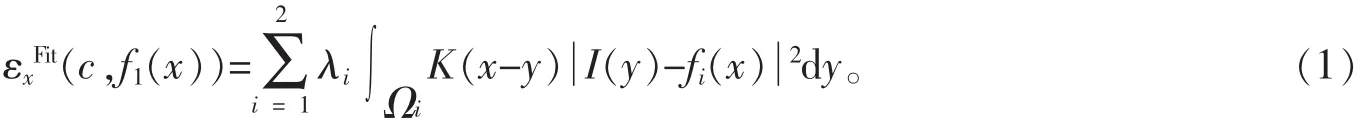
式（1）中：K为核函数，用于控制x的邻域Ox=r为领域半径；Ω1=in（c），Ω2=out（c），分别为对应邻域的背景和目标邻域；f1（x）和f2（x）为图像在点x处的2个局部拟合值；λ1，λ2为内外能量差的权重项，且均为正数。其相应的水平集表达式为：

式（2）中：x∈Ω，φ为水平集函数，λ1，λ2为内外能量差的权重项，M1（φ），Hε（φ），M2（φ）=1-Hε（φ），Hε（x）是Heaviside函数，当且仅当曲线位于目标的边界时，式（1）取得极小值即LBF能量取得极小值。其中：

式（3）～（5）中：Kσ（x）为σ＞0的高斯函数，对于每个水平集函数φ，根据式（4）和式（5），可知f1（x）和f2（x）为图像在点x局部邻域的加权灰度平均值（邻域大小由高斯函数的方差σ决定）。将当前点x延伸到整个图像区域，同时为了确保水平集函数φ演化的稳定性，增加曲线长度项L（x）以及距离保证项［13］。从而得出总能量函数：

根据变分法和梯度下降法，对式（6）可得能量泛函梯度下降流的水平集演化的偏微分方程式为：

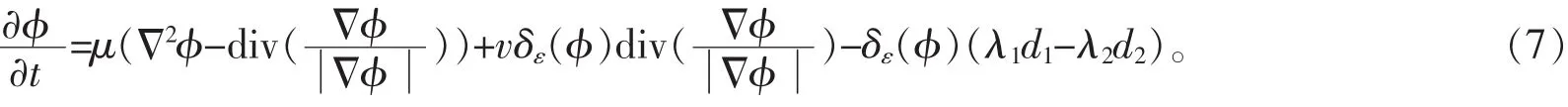
式（7）中：Δ2为拉普拉斯算子；div（

）为散度算子；δε（x）是Dirac函数。

式（8）～（10）中：f1，f2分别近似于当前点x邻域中位于演化曲线内部和外部区域的灰度均值，且利用点x扩展到整个图像区域内各个像素点的灰度值与f1和f1相差的大小来驱使演化曲线运动。分割弱边界图像时，水平集演化方程式（7）中的d1和d2将会趋近于0，使得能量方程达到最小值，导致曲线演化停止，分割结束［13］。

1.2LBF模型的高斯核函数改进模型

LBF模型拟合的灰度值区域的范围由引入的非负核函数的参数大小来确定。根据高斯核函数的局部化特性，距离x越近的点对于该点能量的贡献越大，当距离大于时，对点能量的影响几乎为0［14］。所以，引入高斯核函数对于LBF模型的不均匀的灰度信息创造了条件［15］。根据式（1）可知0水平集局部拟合能量方程，其中高斯核函数通常表达式为：

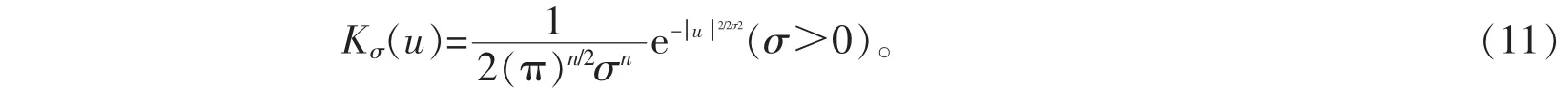
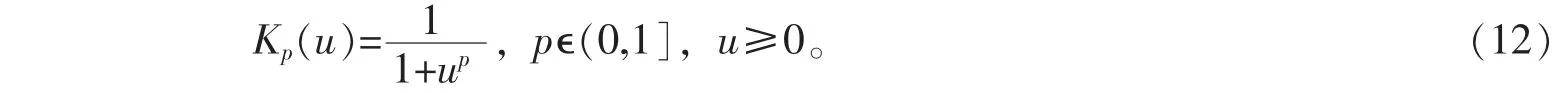
要求p∈（0,1］，是因为p＞1时，Kp（u）具有与高斯函数相似的图形特征——存在拐点x=（（p-1）/（p+1））1/p下降快。综上所述，将方程（6）与方程（7）中的Kσ用替代Kp，得到改进的LBF模型的演化方程如下：

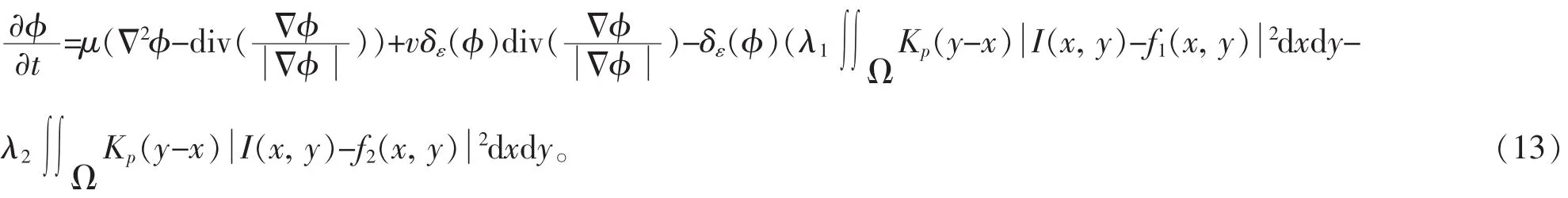
LBF模型利用局部图像信息，而没有考虑图像的局部方差信息和全局方差信息，因此用该核函数代替高斯函数，对LBF模型进行了改进，可以对不均匀图像有更好的分割效果，并且加快了LBF模型的演化速度［11］。

2　试验结果与分析

根据国家板材标准GB/T 4823-1995《锯材缺陷》，板材表面缺陷图像一般有虫眼、活节和死节。实验过程中使用的图像为具有单个活节、虫眼、死节板材缺陷图像和具有多个活节、虫眼、死节的板材缺陷图像，且使用的图像均为灰度分布不均匀图像。LBF模型分割过程中每次的迭代任务就是完成局部特征值f1（x）和f2（x）以及水平集函数的更新，根据检测0水平集变化来确定迭代是否收敛。简而言之，当连续n次0水平集的变化均小于2个像素时（实验中n取5次），则迭代收敛。实验算法的参数若无特别说明均设置为：权重系数λ1=1.0，λ2=1.5；正则化参数ε=1.0；时间步长为Δt=0.1；长度权值μ=1.0；核函数的方差根据不同缺陷图像而定。

2.1单个目标的分割实验结果

2.1.1单个活节分割结果图1为单个活节实验样本的原图和灰度图。从活节的灰度图可得出：活节灰度值与周围正常板材组织灰度值的像素差距较小，且边缘模糊不太清晰。图2为本研究算法对单个活节进行分割的过程，算法核函数的方差设置为σ=5.0。其中图2A迭代次数为50次,分割时间为5.366 4 s；图2B迭代次数为80次，分割时间为8.673 7 s；图2C迭代次数为100次，分割时间为10.592 5 s。图3为本研究算法对单个活节分割过程产生的水平集演化图像，其中，图3A迭代次数为50次，图3B迭代次数为80次，图3C迭代次数为100次。

图1　活节原图与灰度图Figure 1 An original image and gray image of the slipknot

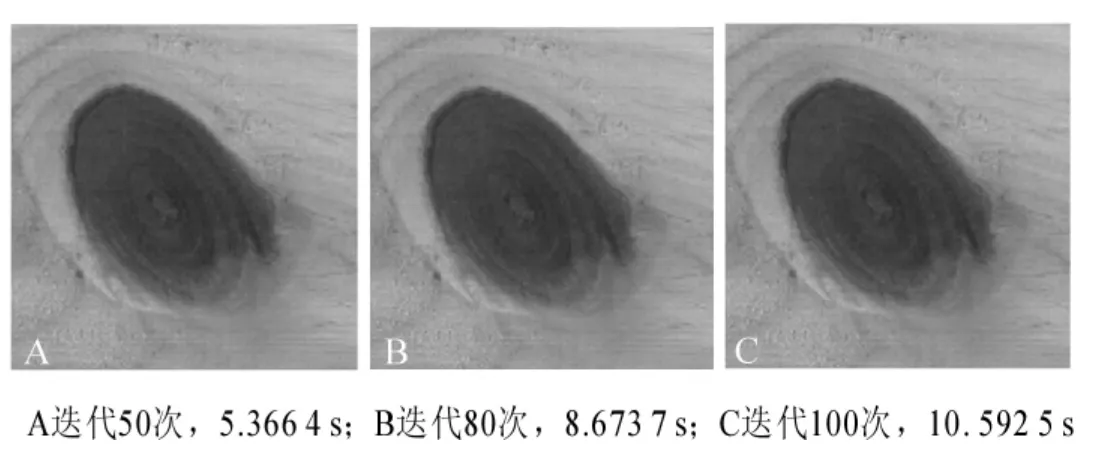
图2　活节分割过程Figure 2 Segmentation process of the slipknot

2.1.2单个虫眼分割结果图4为单个虫眼实验样本的原图和灰度图。从虫眼的灰度图可得出虫眼的灰度值与周围正常板材组织灰度值的像素差距较大，且灰度分布不均匀。图5为对单个虫眼进行分割的过程，算法核函数的方差设置为σ＝3.5。其中图5A迭代次数为50次,分割时间为2.558 4 s；图5B迭代次数为80次，分割时间为5.912 4 s；图5C迭代次数为100次，分割时间为8.439 7 s。图6为本研究算法对单个活节分割过程产生的水平集演化图像，其中，图6A迭代次数为50次，图6B）迭代次数为80次，图6C迭代次数为100次。

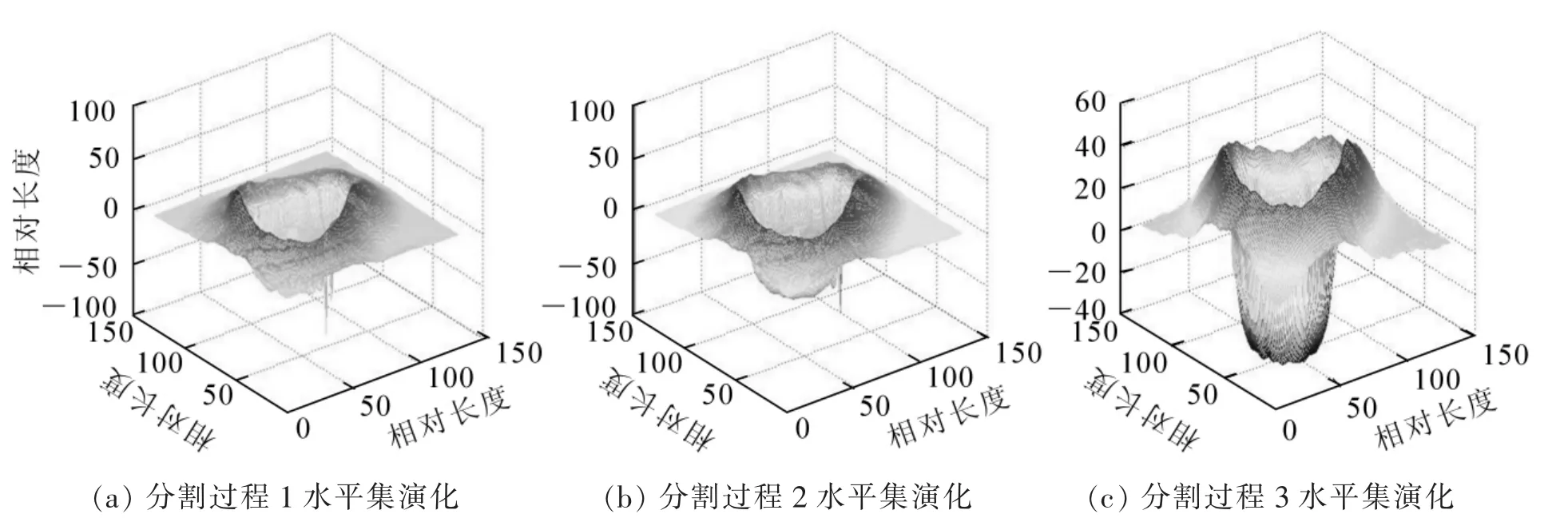
图3　活节分割过程水平集演化Figure 3 Level set evolution of segmentation process of the slipknot

图4　虫眼原图与灰度图Figure 4 An original image and gray image of the wormhole

图5　虫眼分割过程Figure 5 Segmentation process of the wormhole

2.1.3单个死节分割结果图7单个死节实验样本的原图和灰度图。图8为对单个死节进行分割的过程，算法核函数的方差设置为σ＝3.5。其中图8A迭代次数为50次,分割时间为13.915 3 s；图8B迭代次数为100次，分割时间为27.534 2 s；图8C迭代次数为150次，分割时间为41.652 3 s。图9为对单个活节分割过程产生的水平集演化图像，其中，图9A迭代次数为50次，图9B迭代次数为100次，图9C迭代次数为150次。

图6　虫眼分割过程水平集演化Figure 6 Level set evolution of segmentation process of the wormhole

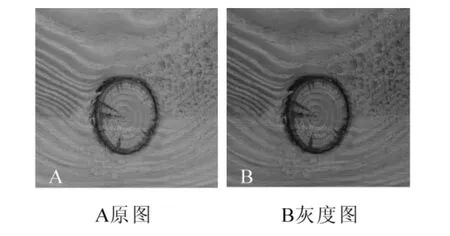
图7　死节原图和灰度图Figure 7 An original image and gray image of the encased knot

图8　死节分割过程Figure 8 Segmentation process of the encased knot

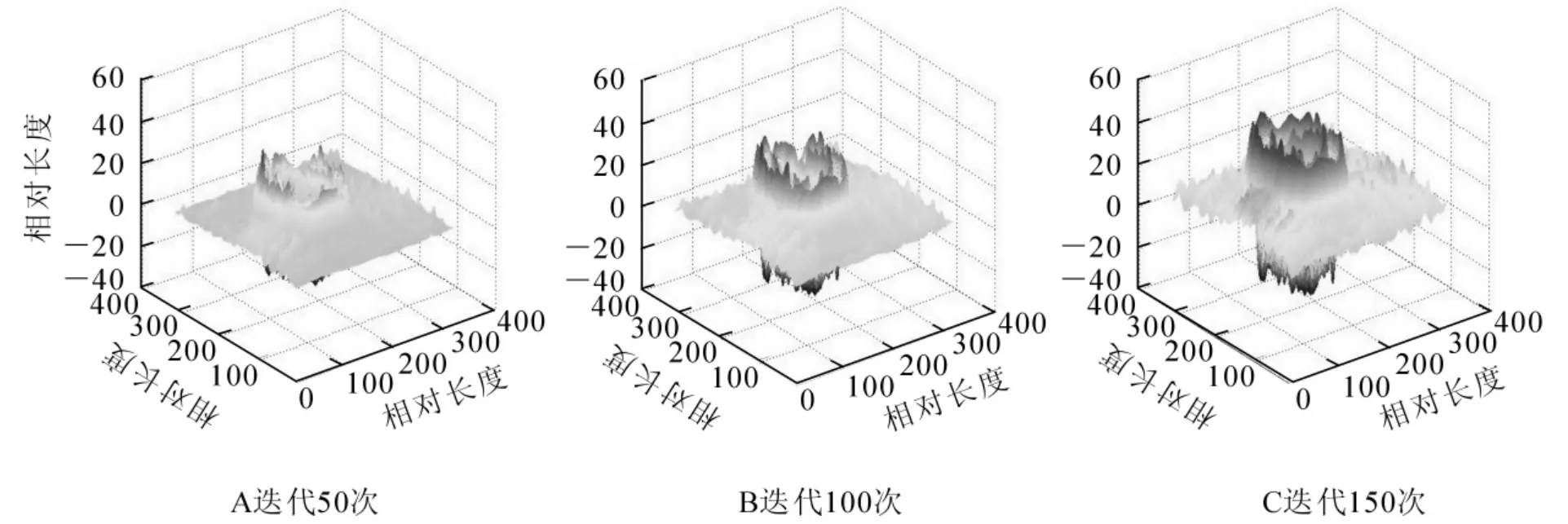
图9　死节分割过程水平集演化Figure 9 Level set evolution of segmentation process of the encased knot

2.2多个目标的分割实验结果

2.2.1多个活节分割结果图10为多个活节实验样本的原图和灰度图。图11为对多个死节进行分割的过程，算法核函数的方差设置为σ＝3.5。其中图11A迭代次数为30次,分割时间为6.130 8 s；图11B迭代次数为40次，分割时间为7.332 0 s；图11C迭代次数为50次，分割时间为41.652 3 s。图12为对多个活节分割过程产生的水平集演化图像，其中，图12A迭代次数为30次，图12B迭代次数为40次，图12C迭代次数为50次。

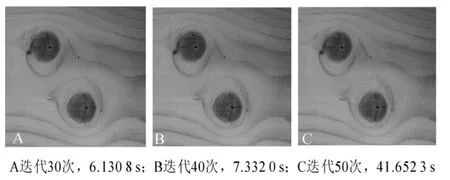
图11　多活节分割过程Figure 11 Segmentation process of the slipknots

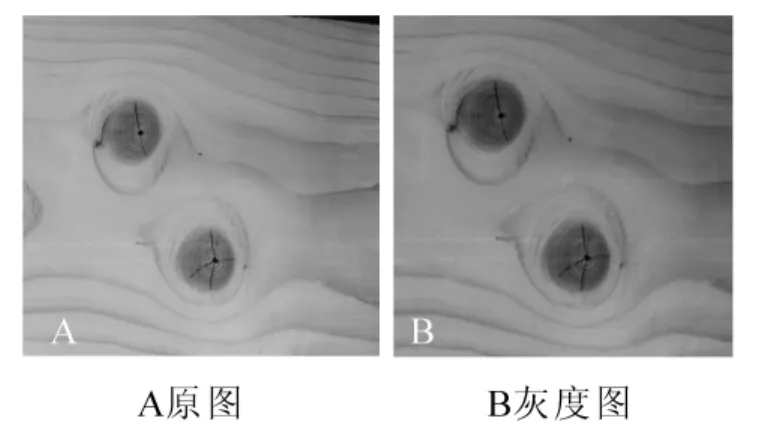
图10　多活节原图与灰度图Figure 10 An original image and gray image of the slipknots

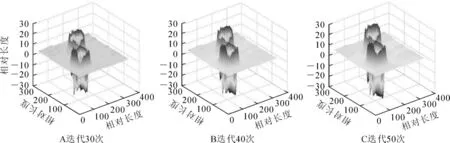
图12　多活节分割过程水平集曲线Figure 12 Level set evolution of segmentation process of the slipknots

2.2.2多个虫眼分割结果图13为多个虫眼实验样本的原图和灰度图。图14为对多个虫眼进行分割的过程，算法核函数的方差设置为σ＝5.5。其中图14A迭代次数为20次,分割时间为7.035 6 s；图14B迭代次数为30次，分割时间为10.374 1 s；图14C迭代次数为40次，分割时间为13.816 9 s。图15为对多个虫眼分割过程产生的水平集演化图像，其中，图15A迭代次数为20次，图15B迭代次数为30次，图15C迭代次数为40次。

图13　多虫眼原图与灰度图Figure 13 An original image and gray image of the wormholes

图14　多虫眼分割过程Figure 14 Segmentation process of the wormholes

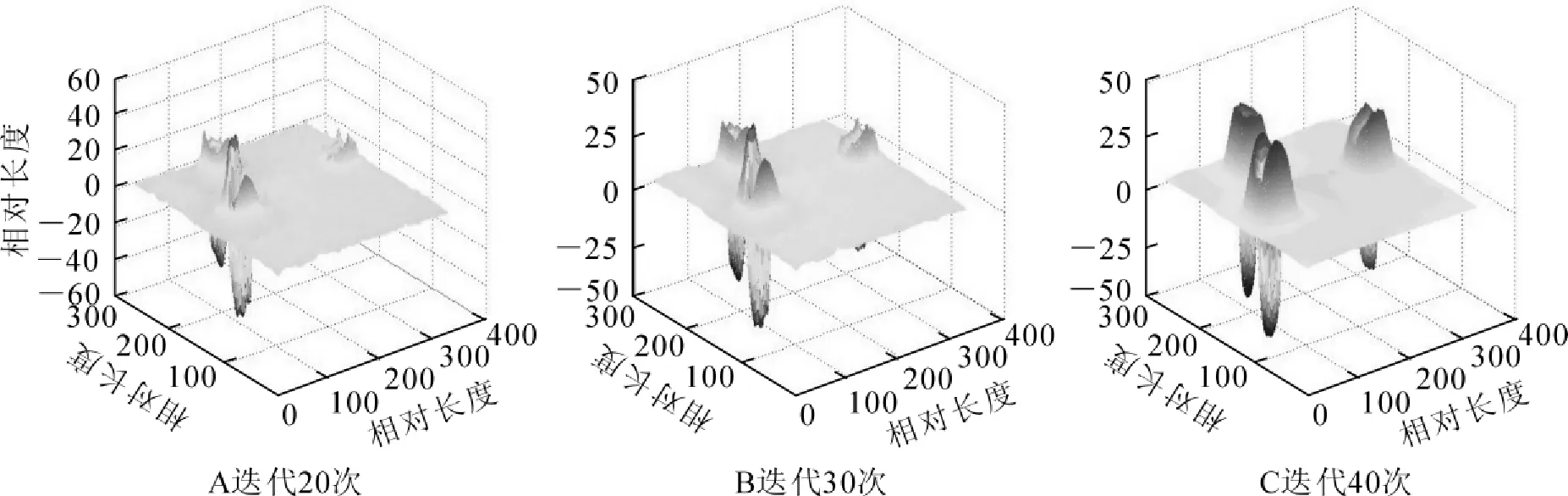
图15　多虫眼分割过程水平集演化Figure 15 Level set evolution of segmentation process of the wormholes

2.2.3多个死节分割结果图16所为多个死节实验样本的原图和灰度图。图17为对多个死节进行分割的过程，算法核函数的方差设置为σ＝5.5。其中图17A迭代次数为20次,分割时间为3.198 0 s；图17B迭代次数为30次，分割时间为5.070 0 s；图17C迭代次数为40次，分割时间为13.816 9 s。图18为对多个死节分割过程产生的水平集演化图像，其中：图18A迭代次数为20次，图18B迭代次数为30次，图18C迭代次数为40次。

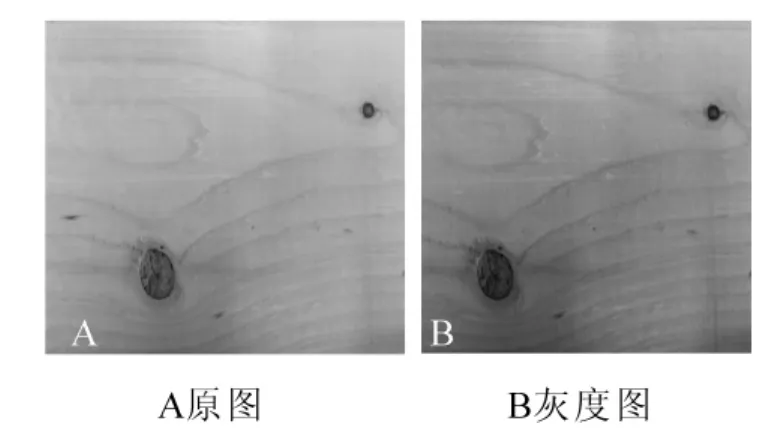
图16　多死节原图与灰度图Figure 16 An original image and gray image of the encased knots

图17　多死节分割过程Figure 17 Segmentation process of the encased knots

图18　多死节分割过程水平集演化Figure 18 Level set evolution of segmentation process of the encased knots

2.3复杂背景下改进LBF模型的板材表面节子和虫眼的图像分割

为了验证改进LBF模型算法对板材表面缺陷分割的实用性以及检测1.0 m长板材内的节子和虫眼个数，因而对复杂背景的1.0 m长整块板材的图像进行研究，原图像如图19所示，分割结果如图20所示，分割结果对应的水平集演化如图21所示。观察最终分割结果图可知改进LBF模型算法能够将缺陷从整个复杂背景下有效地分割出来，不受到形状、位置、面积大小等限制，同时也不受到木材自身纹理的干扰，分割轮廓线能够快速地收敛到缺陷边界，整个分割过程曲线演化平滑，分割结果比较理想。迭代次数分别为300次、470次、400次。运行时间分别为57.517 0 s，63.523 0 s，56.772 0 s。

图19　复杂背景下整块板材表面原图像Figure 19 Original images of wood surface under complex background

图20　整块板材的分割结果Figure 20 Segmentation results of block plate

图21　分割结果对应的水平集演化Figure 21 Level set evolution of segmentation results

2.4实验分析

本研究实验结果表明：改进的LBF模型能够分割出灰度不均一的图像，同时能比较完整地提取出单一目标和多目标的板材表面缺陷图像。通过实验得出改进模型的分割结果并不完全依赖于演化曲线的大小与轮廓的初始位置，而且避免了水平集函数在实验过程中出现震荡现象，从而降低了数值计算的误差。基本克服了噪声对实验结果的影响，得出与缺陷图像相对应的较稳定的水平集演化图像。该算法对比于其他分割方法，分割的迭代次数较少，分割的速度较快，分割结果也更加完整。表1为板材表面缺陷系统分割结果。

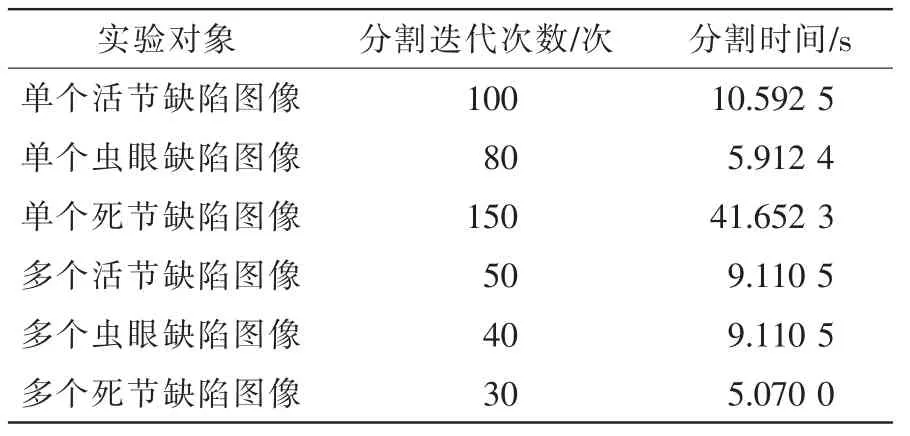
表1　板材表面缺陷系统分割结果Table 1 Segmentation results of wood surface defect system

3　结论

研究表明：采用改进的LBF算法对3种板材表面缺陷的分割效果都很理想。通过对单一目标与多个目标分割时间的比较，得出该算法对多个目标的分割速度更快。相对于活节与虫眼的分割，该算法对死节的分割时间较长，但是分割时间控制在50.000 0 s内。通过实验得出本研究改进的LBF模型可以通过选择恰当的实验参数，对板材表面缺陷的图像进行有效分割，获得比较完整的闭合分割曲线轮廓。不仅可以进行单个目标的分割，还可以进行多个目标的分割，而且对初始轮廓的大小和位置不敏感，抗噪性较强，分割速度快，分割效果好。根据对复杂背景下的整块板材图像的分割，可以清楚地得出改进LBF模型算法能够将缺陷从整个复杂背景下有效地分割出来，而且不受形状、位置和面积大小的限制，并且能比较准确的检测出单位面积内板材表面节子和虫眼的个数。

4　参考文献

［1］王林.基于Gabor变换的木材表面缺陷识别方法的研究［D］.哈尔滨：东北林业大学，2010.WANG Lin.Research on Recognition Method of Wood Surface Defects Based on Gabor Transformation［D］.Harbin: Northeast Forestry University, 2010.

［2］WANG J, BIERNACKI J M, LAM F.Nondestruetive evaluation of veneer quality using acoustic wave measurements ［J］.Wood Sci Technol, 2001, 34（6）: 505×516.

［3］张芹，侯德文.一种结合区域梯度的自适应CV模型［J］.计算机应用与软件，2014，31（3）：214 - 216.ZHANG Qin, HOU Dewen.An adaptive CV model combining regional gradient［J］.Comput Appl Software, 2014, 31（3）: 214 - 216.

［4］DU Xiaojun, BUI T D.A new model for image segmentation［J］.IEEE Sign Proc Lett, 2008, 15: 182 - 185.

［5］何瑞英.含边缘信息的C-V模型［J］.计算机工程与应用，2012，48（18）：181 - 186.HE Ruiying.C-V model with edge information［J］.Comput Eng Appl, 2012, 48（18）: 181 - 186.

［6］张少华.结合全局与局部信息的活动轮廓模型研究［D］.重庆：重庆大学，2011.ZHANG Shaohua.Study on Active Contours Integrating Global and Local Information［D］.Chongqing: Chongqing U-niversity, 2011.

［7］原野，何传江.LBF活动轮廓模型的改进［J］.计算机工程与应用，2009，45（15）：177 - 179.YUAN Ye, HE Chuanjiang.Improvement of LBF active contours model［J］.Comput Eng Appl, 2009, 45（15）: 177 -179.

［8］潘改，高立群，赵爽.基于局部熵的主动轮廓模型［J］.中国图像图形学报，2013，18（1）：78 - 85.PAN Gai, GAO Liqun, ZHAO Shuang.Active contour model driven by local entropy energy［J］.J Image Graph, 2013, 18（1）: 78 - 85.

［9］LI Chunming, KAO C Y, GORE J C, et al.Implicit active contours driven by local binary fitting energy［C］//Proc.of IEEE Conference on Computer Vision and Pattern Recognition.Minnesota:［s.n.］.2007: 1- 7.

［10］吴永飞，何传江，陈强.基于CV和LBF模型结合的图像分割算法研究与实现［J］.计算机应用与软件，2013，30（7）：98 - 100.WU Yongfei, HE Chuanjiang, CHEN Qiang.Research and implementation of image segmentation algorithm based on CV and LBF model［J］.Comput Appl Software, 2013, 30（7）: 98 - 100.

［11］张少华.带线性正则化项的RSF模型［J］.计算机工程与应用，2011，47（24）：160 - 163.ZHANG Shaohua.RSF model with linear regularization item［J］.Comput Engi Appl, 2011, 47（24）: 160 - 162.

［12］代双语，王智峰，张学东.结合局部与全局信息的主动轮廓模型［J］.辽宁科技大学学报，2013，36（2）：145 - 150.DAI Shuangyu, WANG Zhifeng, ZHANG Xuedong.Active contour model by combining with local and global information［J］.J Univ Sci Technol Liaoning, 2013, 36（2）: 145 - 150.

［13］王顺凤.基于改进的LBF模型的图像分割［J］.计算机应用与软件，2011，28（2）：25 - 27.WANG Shunfeng.Image segmentation based on improved LBF model［J］.Comput Appl Software, 2011, 28（2）: 25 -27.

［14］刘学.基于特征的彩色图像配准技术研究［D］.长沙：国防科学技术大学，2010.LIU Xue.Study on Colored Image Registration Based on Feature［D］.Changsha: National Defense Science and Technology University, 2010.

［15］徐海勇，陈军刚.一种新的基于局部区域的活动轮廓模型［J］.湖南理工学院学报：自然科学版，2012，25 （1）：42 - 45.XU Haiyong, CHEN Jungang.An ovel local region-based active contours model［J］.Hunan Inst Sci Technol Nat Sci, 2012, 25（1）: 42 - 45.

Segmentation of wood surface knots and wormholes based on an improved LBF Model

BAI Xuebing, XU Jingtao, GUO Jingqiu, CHEN Kai
（College of Machinery Electricity, Northeast Forestry University, Harbin 150040, Heilongjiang, China）

Abstract:To make wood surface defect segmentation faster and more effective, research was conducted to put forward an improved LBF（local binary fitting）Model with image segmentation based on the Chan-Vese（CV）

Model.The improved LBF Model added a new level set formulation with a linear regularization term, and at the same time formed a Gaussian function as the kernel function with two local values for fitting energy.Results showed that the improved algorithm could overcome the segmentation shortcomings in the LBF Model.Also, the segmentation process was not sensitive to the size or the position of the initial contour.However, the anti noise of the algorithm was enhanced, and the image could be segmented in non-uniform gray.The experiment showed that the algorithm completely extracted the wood surface defect images with single and multi objectives, and

level set evolution corresponding to the defect image could be obtained.［Ch, 21 fig.1 tab.15 ref.］

Key words:wood science and technology; wood surface defects; wood image segmentation; LBF model; level set

作者简介：白雪冰，教授，从事图像处理与模式识别研究。E-mail：xumou2010@163.com

基金项目：黑龙江省自然科学基金资助项目（C201208）

收稿日期：2015-04-20；修回日期：2015-09-16

doi:10.11833/j.issn.2095-0756.2016.02.017

中图分类号：TP391.41；S781.1

文献标志码：A

文章编号：2095-0756（2016）02-0306-09