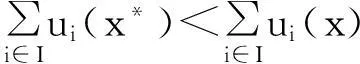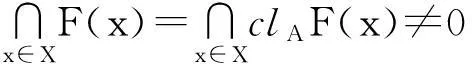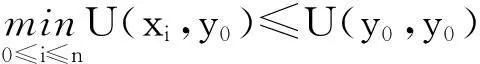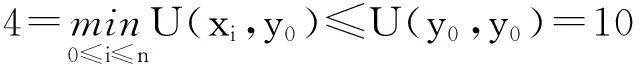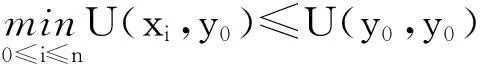一类非连续博弈的帕累托有效纳什均衡的存在性

刘志刚，侯吉成

(北京信息科技大学理学院，北京　100192)



一类非连续博弈的帕累托有效纳什均衡的存在性

刘志刚，侯吉成

(北京信息科技大学理学院，北京100192)

摘要：在拓扑空间结构下，给出了一类新的n人非合作非连续博弈的帕累托有效纳什均衡的存在性定理，并且提供了一些实际例子，其结果能够验证其帕累托有效纳什均衡的存在性.

关键词：帕累托有效纳什均衡；C-拟凹；对角转移连续

【引用格式】刘志刚，侯吉成.一类非连续博弈的帕累托有效纳什均衡的存在性[J].北华大学学报(自然科学版)，2016，17(2)：154-158.

1引言

纳什均衡[1]是博弈论中最重要的概念之一.它不受单向偏离的影响，也就是说，只要是其他人没有偏离他的策略，那么每个人就没有想偏离这个策略的动机.然而，在现实的经济系统中，考虑帕累托有效也是有重要的实际意义的.因为帕累托有效策略组合是指这样的经济系统：偏离这个策略组合选择组合的任何其他行动选择组合都至少会使一个人的境况变差.显然，纳什均衡不一定是帕累托有效的.反过来，帕累托有效策略组合也不一定是纳什均衡.的确，在囚徒困境中，策略组合(不认罪，认罪)、(认罪，不认罪)和(不认罪，不认罪)都是帕累托最优的，但不是纳什均衡.另一方面，策略组合(认罪，认罪)是纳什均衡，但不是帕累托有效的.然而这对矛盾在性别战博弈中不存在，甚至这两个概念达成统一.因此，这就产生一个公开问题：对何种博弈，帕累托有效纳什均衡存在？这就成了纯策略博弈中的基本问题之一.

1959年，Aumann[2]已经介绍了强纳什均衡是帕累托有效的；1983年，Ichiishi[3]给出了帕累托有效纳什均衡存在性的一个充分条件；2008年，Rabia Nessah[4]研究了strong Berge均衡的性质，指出了strong Berge均衡也是帕累托有效的.然而，有关这些典型的帕累托有效纳什均衡存在性定理中，效用函数的假定都是连续的.

最近，Vincenzo Scalzo[5]首先在非连续博弈中给出了一累帕托有效纳什均衡存在性的充分条件：

定理1设X是拓扑线性空间中的紧凸子集.假设：

(A2)函数U(·，z)，∀z∈X是严格拟凹的，即：∀x1，x2，z∈X(x1≠x2)有

U(xλ，z)>min{U(x1，z)，U(x2，z)}，∀λ∈(0，1)，

其中xλ=(1-λ)x1+λx2；

(A3)若x是F的最大点，且z∈X{x}，那么存在λ0∈(0，1)，使得

则博弈G至少有一个帕累托有效纳什均衡点.

在本文中，我们的目的是在没有任何线性结构下的拓扑空间中，通过一类拓扑方法和KKM引理，减弱了定理1中的严格拟凹性，建立一类n人非合作非连续博弈下的帕累托有效纳什均衡存在性定理.我们的方法与定理1中的方法有着本质的不同，我们的方法十分经典，而且容易验证.此外，我们提供了一些实际例子，定理1的条件不能适应，而我们的定理能够验证这些实际例子的帕累托有效纳什均衡的存在性.

以下我们给出了一些后文需要用到的定义和需要注意的术语.

设A表示拓扑空间X的子集，clXA表示A在X中的闭包，2A表示A的所有非空子集族.令Δn为n+1中的n维单纯形，如果{ei；i=1，2，…，n}为Δn中的标准基，我们用co{ei；i∈S}表示{ei；i∈S}的凸包，其中S⊆{1，2，…，n}.

考虑以下标准的非合作博弈模型：

G=(Xi，ui)i∈I，

其中I={1，2，…，n}是有限个局中人的集合，Xi是局中人i的策略空间，在本文中假设它们是豪斯多夫拓扑空间，ui：Xi→为局中人i的效用函数.

策略组合x*∈X是n人非合作博弈G的纳什均衡是指：

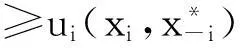
2主要结论

为了得到我们的主要结论，首先给出之后会用到的一些经典的概念和结论.

引理1[6]x*∈X是博弈G的纳什均衡当且仅当对于所有的y∈X，有U(x*，x*)≥U(y，x*).

定义1[5]策略组合x*是帕累托有效的，如果不存在策略组合x，使得ui(x*)≤ui(x)，∀i∈I，而且至少存在一个h∈I，使得uh(x*)

定义2[7]设Y是拓扑空间，A⊆Y，函数f：Y→在A上是转移上连续的，如果对于任何x，y∈A，f(y)

引理2[7]设Y是拓扑空间中的紧子集，f：Y→是一个对应，则f的最大值点集在Y上是非空且紧致的当且仅当f在Y上是转移上连续的.

定义3[8]设Y是拓扑空间，A⊆Y，函数U：Y×A→在y∈Y处是对角转移连续的，如果对于(x，y)∈Y×A，U(x，y)>U(y，y)，x′∈Y和y的某个邻域Ny，使得U(x′，y′)>U(y′，y′)，∀y′∈A∩Ny.

定义4[9]设Y是拓扑空间，A⊆Y.函数U：Y×A→在Y上是C-拟凹的，如果对于任意{y0，y1，…，yn}⊆Y，存在连续映射φn：Δn→A，使得

min{U(xi，φn(λ))：i∈J}≤U(φn(λ)，φn(λ))，∀(λ0，λ1，…，λn)∈Δn，

其中J={i∈{0，1，…，n}：λi≠0}.

C-拟凹性比拟凹性更弱(参阅文献[9]的命题1).

(B1)F：x在A上是转移上连续的；

那么博弈G至少存在一个帕累托有效纳什均衡点.

证明：结合引理2和假设(B1)，可知集合A非空且紧致.设x*∈A，我们将证明x*是帕累托有效点.如果不是，那么x∈X，使得ui(x*)≤ui(x)，∀i∈I，且存在h∈I，使得uh(x*)

即U(x*，x*)

我们再定义集值映射F：X→2A，其中：

F(x)={y∈A：U(x，y)

(1)

其中(λ0，λ1，…，λn)∈Δn，I(λ)={i：λi≠0}.

设{ei：i=0，1，…，n}是Δn的标准基.从式(1)知：对于任意S⊆{0，1，…，n}，有

现在我们将给出一些实例，定理1不能验证，但是我们的定理条件能保证帕累托有效纳什均衡的存在.

例1考虑一类博弈G，其中n=2，X1=X2=[0，1]，ui(x1，x2)=xi-0.5.

我们取x=(1，0)，x′=(0，1)，y=(1，1)，λ=1/2，x″=(1/2，1/2)，有

min{U(x，y)，U(x′，y)}=U(x″，y)=0.

因此定理1的条件(A2)不满足.故定理1不能使用.

因为U(x，y)=x1+x2-1，对任意(x，y)∈X×A，没有U(x，y)>U(y，y).因此定理2条件(B2)被满足.

例2考虑以下由Larbani，Nessah[10]引入的一类博弈，假设I={1，2，3}，Xi=[0，1]，∀i∈I，且效用函数分别为：

其中x=(x1，x2，x3).容易得到

不难验证A=argmaxF(x)=argmaxU(x，x)={(1，1，1)}.因为A是X=[0，1]3中的非空且紧致集，由引理2知定理2条件(B1)被满足.

对于任意x=(x1，x2，x3)，y=(y1，y2，y3)∈X，有

且对任意(x，y)∈X×A，不存在U(x，y)>U(y，y).由此知条件(B2)被满足.

其中y0=(1，1，1)，得证.故定理2的条件(B3)也满足.因此该博弈存在帕累托有效纳什均衡点.

但是定理1中的严格拟凹性条件(A2)不被满足.因为取x=(1，0，0)，x′=(0，1，0)，λ=1/2，x″=(1/2，1/2，0)，则有

U(x″，y)=min{U(x，y)，U(x′，y)}.

例3考虑一类2人博弈，策略空间是单位闭区间.这是在图洛克寻租博弈[11]中受启发而得到的.支付函数ui(x1，x2)(i=1，2)由下式给定：

注意到

首先易知A=argmaxF(x)=argmaxU(x，x)={(0，0)}，因此A在X=[0，1]2中是非空且紧致的，由引理2知定理2条件(B1)满足.

其次，对任意x=(x1，x2)，y=(y1，y2)∈X，我们有：

因为y1=y2=0，故不存在U(x，y)>U(y，y)，其中y=(y1，y2)=(0，0).因此定理2条件(B2)满足.

1=U(x″，y)=min{U(x，y)，U(x′，y)}.

参考文献：

[1] Nash J F.Non-cooperative games[J].Ann Math Stud，1951，54(3)：286-295.

[2] Aumann R J.Acceptable points in general cooperativen-person games[M].Princeton：Princeton University Press，1959：287-324.

[3] Ichiishi T.Game theory for economic analysis[M].New York：Academic Press Inc，1983：151-156.

[4] R Nessah，T Tazdait，M Larbani.Strong Berge and Pareto equilibrium existence for a non-cooperative game[J].Working Paper，2008.

[5] Scalzo V.Pareto efficient Nash equilibria in discontinuous games[J].Economics Letters，2010，107(3)：364-365.

[6] Tian G.Existence of equilibria in games with arbitrary strategy spaces and payoffs：A full characterization[J].Levine S Working Paper Archive，2009.

[7] Tian G，Zhou J.Transfer continuities，generalizations of the Weierstrass and maximum theorems：a full characterization[J].Journal of Mathematical Economics，1995，24(3)：281-303.

[8] Baye M R，Tian G，Zhou J.Characterizations of the existence of equilibria in games with discontinuous and non-quasiconcave payoffs[J].Review of Economic Studies，1993，60(4)：935-948.

[9] Hou J C.Characterization of the existence of a pure-strategy Nash equilibrium[J].Applied Mathematics Letters，2009，22(5)：689-692.

[10] Larbani M，Nessah R.A note on the existence of Berge and Berge Nash equilibria[J].Mathematical Social Sciences，2008，55(2)：258-271.

[11] Lockard A，Tullock G.Efficient rent-seeking[M].New York：Springer Netherlands，2009.

【责任编辑：伍林】

Existence of Pareto Efficient Nash Equilibrium in Discontinuous Games

Liu Zhigang，Hou Jicheng

(SchoolofAppliedScience，BeijingInformationScienceandTechnologyUniversity，Beijing100192，China)

Abstract：We give a new existence theorem on Pareto efficient Nash equilibrium for discontinuous n-person non-cooperative games in the framework of topological spaces without any linear structures.Moreover，we provide some examples，which results can verify existence of Pareto efficient Nash equilibrium.

Key words：Pareto efficient Nash equilibrium；C-quasiconcavity；diagonally transfer continuity

中图分类号：O225

文献标志码：A

作者简介：刘志刚(1990-)，男，硕士，主要从事博弈论、非线性分析研究，E-mail：715527201@qq.com；通信作者：侯吉成(1963-)，男，博士，教授，硕士生导师，主要从事博弈论、拓扑学及非线性分析研究，E-mail：houjc163@163.com．

基金项目：国家自然科学基金项目(11271178).

收稿日期：2015-12-26

文章编号：1009-4822(2016)02-0154-05

DOI：10.11713/j.issn.1009-4822.2016.02.003