一种哈夫曼编码的改进算法

王防修，刘春红

(1.武汉轻工大学 数学与计算机学院，湖北 武汉 430023；2.九州通医药集团物流有限公司，湖北 武汉 430040)



一种哈夫曼编码的改进算法

王防修1，刘春红2

(1.武汉轻工大学 数学与计算机学院，湖北 武汉 430023；2.九州通医药集团物流有限公司，湖北 武汉 430040)

摘要：针对哈夫曼编码需要用到指针和结构体而导致使用受到限制的问题，提出一种不用指针和结构体也能进行哈夫曼编码的算法。算法以哈夫曼编码的编码原理为基础，先自底向上得到各个中间结点的双亲结点和孩子结点，然后自顶向下得到各个结点的二进制码字，最后得到的叶子结点的码字就是哈夫曼编码。由于所设计的哈夫曼编码算法只需要使用一维数组即可以实现，故对完成编码的计算机语言没有任何限制。算例仿真表明，使用三个一维数组即可实现任何事件的哈夫曼编码。

关键词：哈夫曼编码；中间结点；码字；叶子结点

1引言

作为一种压缩率最高的无损压缩编码[1]，哈夫曼编码的算法实现一直是人们关注的热点问题[2-5]。在哈夫曼编码的计算机实现过程中，普遍都需要使用指针和结构体构造哈夫曼树。然而，许多计算机高级语言并不支持指针和结构体，比如常用的basic语言。同样，许多网络语言也不支持指针和结构体，比如vbscript脚本语言。如果能够设计一个不需要指针和结构体的哈夫曼编码算法，则哈夫曼编码的使用可以得到进一步推广[6-8]。因此，本文研究并设计一种不需要指针和结构体也可实现哈夫曼编码的算法。

2哈夫曼编码的原理

设xi(i=1,2,…,n)是信源S的n个事件，而wi是xi在信源S中出现的频率。由哈夫曼编码的原理，可以得到事件xi对应的编码bi。为了方便计算机实现同时又不能使用指针和结构体，需要探索现有这些变量之间的联系。

2.1中间结点权重的计算

根据哈夫曼编码原理，如果把wi(i=1,2,…,n)看作编码结点的权重，则已经具有哈夫曼编码的n个叶子结点权重。由于哈夫曼编码总共需要2n-1个结点权重，故还需要计算n-1个中间结点的权重wi(i+1,i+2,…,2n-1)。对于第j个中间结点的权重wj而言，其权重是其左右孩子结点的权重之和。因此,要求权重wj,必须先求出它的两个孩子权重。为方便起见,不妨设wj的左孩子权重为wl和右孩子权重为wr。

第j个中间结点的左孩子结点权重的选择算子如下：

(1)

式(1)中的wl表示从所有未被选择的权重中选择最小的权重,其中fi=0表示权重wi没有被选。而式中的fl=-1表示权重wl将作为第j个中间结点的左孩子权重。

第j个中间结点的右孩子结点权重的选择算子如下：

(2)

式(2)中的fr=1表示权重wr将作为第j个中间结点的右孩子权重。

通过式(1)和式(2)可以求出第j个中间结点的左孩子结点权重wl和右孩子结点权重wr,则第j个中间结点的权重计算如下：

(3)

式(3)中fj=0表示权重wj可以进一步作为其它尚未求出权重的中间结点的子权重。

当wl和wr分别被选择为第j个中间结点的左右孩子权重后,然后通过式(3)求出第j个中间结点的权重wj后,为了方便接下来的哈夫曼编码,需要更新wl和wr的值,更新过程如下：

wl=wr=j.

(4)

式(4)中的wl和wr被用来保存第l个结点和第r个结点的双亲结点位置j。

当计算出所有中间结点的权重之后,除了第2n-1个结点的权重w2n-1存储所有非根结点的权重之和外,其他权重变量wi保存的都是其双亲结点的位置。同样,只有f2n-1=0,其它的标志变量fi不是-1就是1。总之,接下来变量wi和fi将作为求码字bi的依据。

2.2求每个结点的码字

设bi(i=1,2,…,2n-1)是第i个结点的码字,则需要先求出其双亲结点的码字,然后才能求出孩子结点的码字。

首先,根结点不需要编码,故做如下的初始化工作：

b2n-1=w2n-1=0.

(5)

式(5)中b2n-1=0是方便后继结点的编码而设置的,而w2n-1=0表示第2n-1个结点的码字长度为0。

接下来是依次求码字bi,而每个码字只有先求出其双亲的码字,然后才能求出它自身的码字,故求解bi的顺序是下标递减，即i=2n-2,2n-3,…,1。

当求第i个码字bi时,需要根据fi的值来决定编码过程。

如果fi=-1,则bi是双亲结点的左孩子码字,故

bi=2bwi+0.

(6)

如果fi=1,则bi是双亲结点的右孩子码字,故

bi=2bwi+1.

(7)

在式(6)和式(7)中,由于wi表示第i个结点的双亲位置,故第i个结点的编码就是在其双亲码字的末位补上一个二进制位,其中式(6)表示末位补0,而式(7)表示末位补1。

当求出码字bi后, wi已经完成其编码任务。也就是说,此后不再需要用它来保存第i个结点的双亲位置。所以，可以用wi保存码字bi的码长，其计算过程如下：

wi=wwi+1.

(8)

显然,式(8)体现了孩子结点的码长比其双亲结点的码长多1。

3哈夫曼编码的算法实现

从上面的编码原理可知,要想求出某一信源的哈夫曼编码,必须先求出所有中间结点的权重。当计算出所有中间结点的权重后,再由结点之间的关系得到哈夫曼编码。因此,编码算法实现过程分为两个阶段。

3.1求中间结点的权重

对于一个包含n个事件的信源而言,它总共有2n-1个权重,其中n个权重是n个事件在信源中的频率,而其他n-1个权重需要计算得到。具体的求解过程如下：

(1) 初始化。为了从权重序列中选择最小权重,需要设置各权重的初始标志位为0,即令fi=0(i=1,2,…,2n-1)。

(2)令j=n+1,则j表示第一个需要求权重的中间结点的位置。

(3) 由式(1)求出第j个中间结点的左孩子权重wl。

(4) 由式(2)求出第j个中间结点的右孩子权重wr。

(5)由式(3)求出第j个中间结点的权重wj。

(6)由式(4)保存左孩子和右孩子结点的双亲位置。

(7)令j=j+1。如果j≤2n-1,则转步(2)重复进行;否则,求中间结点权重的过程结束。

从上述过程可以看出，求wj是一个递增的过程，即j=n+1,n+2,…2n-1。

3.2求各结点的码字

当所有中间结点的权重计算完成后，除w2n-1保存的是所有结点的权重之和外，其它结点的权重变量wi(i=1,2,…,2n-2)保存的不再是自身权重，而是第i个结点的双亲位置。同样，除了f2n-1=0外，其它标志变量fi(i=1,2,…,2n-2)不是1就是-1。因此，信源的哈夫曼编码的过程如下：

(1)令b2n-1=w2n-1=0和i=2n-2。

(2)如果fi=-1，那么bi=2bwi；否则，bi=2bwi+1。

(3)令wi=wwi+1，表示第i个结点的码长是其双亲的码长加1。

(4)令i=i-1。如果i≥1，则转步(2)重复进行；否则，编码过程结束。

从上述编码过程可以看出，w2n-1=0表明根结点的码字b2n-1是长度为0的空码，而bi是长度为wi的码字，其中i=1,2,…,2n-2。在这里，只有bi(i=1,2,…,n)是前缀码。因此，bi(i=1,2,…,n)就是所求的哈夫曼编码。

4算法仿真

算例1假设有7个信源符号,其频率分布为{20,19,18,17,15,10,1},要求用本文算法对其进行哈夫曼编码。

解首先,叶子结点的权重wi和选择标志fi的初始化，即

w1=20,w2=19,w3=18,w4=17,

w5=15,w6=10,w7=1.

fi=0,i=1,2,…,7.

其次，通过算法3.1求第i个中间结点的权重wi，其中i=8,…,13，其过程如下：

(1)求第8个结点的权重w8及其左右孩子结点选择：

w7=min{w1,w2,w3,w4,w5,w6,w7}

f7=-1。所以w7是左孩子结点权重。因为

w6=min{w1,w2,w3,w4,w5,w6}，f6=1.

所以w7是右孩子结点权重。故

w8=w7+w6=11，f8=0,w6=w7=8.

(2)求第9个结点的权重w9及其左右孩子结点选择：

w8=min{w1,w2,w3,w4,w5,w8},f8=-1.

w5=min{w1,w2,w3,w4,w5},f5=1.

所以w9=w5+w8=26和f9=0,w5=w8=9.

(3)求第10个结点的权重w10及其左右孩子结点选择：

w4=min{w1,w2,w3,w4,w9},f4=-1,

w3=min{w1,w2,w3,w9},f3=1.

所以w10=w3+w4=35,f10=0,w3=w4=10.

(4)求第11个结点的权重w11及其左右孩子结点选择：

w2=min{w1,w2,w9,w10},f2=-1.

w1=min{w1,w9,w10}f1=1.

所以有w11=w1+w2=39,f11=0.w1=w2=11.(5)求第12个结点的权重w12及其左右孩子结点选择：

w9=min{w9,w10,w11},f9=-1.

w10=min{w10,w11},f10=1.

w12=w9+w10=61,w9=w10=12.

(6)求第13个结点的权重w13及其左右孩子结点选择：

w11=min{w11,w12},f11=-1,f12=1.

w13=w11+w12=100,w11=w12=13.

最后，运用算法3.2进行哈夫曼编码。

(1)令b13=Φ。因为w11=w12=13，而f11=-1,f12=1,所以b11=0,b12=1.

(2)因为w9=w10=12，而f9=-1,f10=1,所以b9=10,b10=11.

(3)因为w5=w8=9，而f8=-1,f5=1,所以b5=101,b8=100.

(4)因为w6=w7=8，而f7=-1,f6=1,所以b6=1001,b7=1000.

(5)因为w3=w4=10，而f4=-1,f3=1,所以b3=111,b4=110.

(6)因为w1=w2=11，而f2=-1,f1=1,所以b1=01,b2=00.

算例2假设有4个信源符号，其权重分布为{40,30,20,10},要求用本文算法对其进行哈夫曼编码。

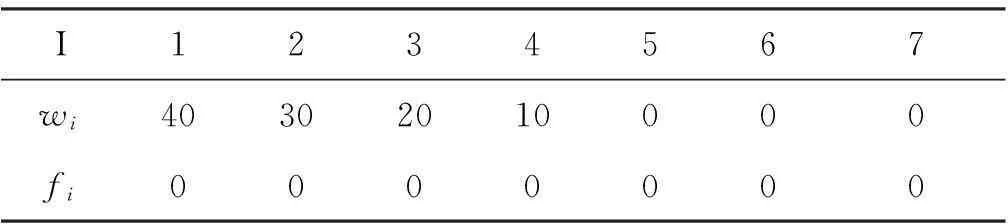
解首先，对结点的权重和选择标志的初始化如表1所示。

表1权重和标志的初始化

I1234567wi40302010000fi0000000

通过算法3.1得到如表2的哈夫曼编码的中间结果。

表2编码的中间结果

I1234567wi765567100fi-1-11-1110

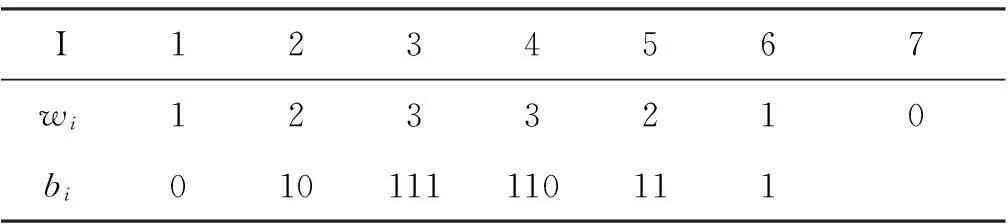
通过算法3.2得到如表3的哈夫曼编码。

表3哈夫曼编码结果

I1234567wi1233210bi010111110111

从表3可以得到对应的哈夫曼编码为{0,10,111,110}。

表1中的wi表示第i个结点的权重, 表2中的wi表示第i个结点的双亲结点的位置, 表3中的wi表示码字bi的码长。

5结束语

笔者提出了一种不用指针和结构体的哈夫曼编码算法。该算法使用一维数组保存各结点的编码信息，在整个编码过程中不需要建立哈夫曼树。无论从算法设计还是算法仿真可以看出，整个算法都只使用一维数组，而数组是任何计算机语言都具有的功能。需要说明的是，前面所说到的双亲结点和孩子结点，只是为方便说明元素之间的关系而已，并不代表该编码需要建立哈夫曼树。根据笔者设计的哈夫曼编码算法，用任何计算机语言都可实现哈夫曼编码，而这对于哈夫曼编码的推广和应用具有重要意义。

参考文献：

[1]叶芝慧,沈克勤.信息论与编码[M].北京:电子工业出版社,2013.

[2]王向鸿.基于Matlab文本文件哈夫曼编解码仿真[J].现代电子技术,2013,36(20):31-32.

[3]薛向阳.基于哈夫曼编码的文本文件压缩分析与研究[J].科学技术与工程, 2010,10(23):5779-5781.

[4]程佳佳,熊志斌.哈夫曼算法在数据压缩中的应用[J].电脑编程技巧与维护,2013(2):35-37.

[5]高健,陈耀.分组无损图像压缩编码方法[J].计算机工程与设计, 2010,31(15):3447-3450.

[6]李灵华,刘勇奎.Freeman四方向链码压缩率提高的方法研究 [J]. 计算机工程与设计,2013,34(3):1132-1136.

[7]王敏超,王敏莉,李秋生，等.无损自适应分布式算术编码的研究及应用[J].计算机工程与设计,2011,32(10)：3470-3475.

[8]王防修,周康,同小军.一种不用构造二叉树的哈夫曼编码[J].武汉工业学院学报,2012,31(2):52-54.

An Improved Algorithm of Huffman Encoding

WANGFang-xiu1,LIUChun-hong2

(1.School of Mathematics and Computer Science,Wuhan Polytechnic University, Wuhan 430023，China;2. Jointown Phamaceutical Group Logistics Co., Ltd. Wuhan 430040,China)

Abstract：According to the application limitation of Huffman encoding due to the need of using the pointer and structure body, a Huffman encoding algorithm without the pointer and structure body was presented in this paper.The algorithm is based on the encoding principle of Huffman encoding.First, from the bottom up to the top it can get the parent node and child nodes of every intermediate node. Second, from the top down to the bottom it can get the binary code of each node. Finally ,codewords of all the leaf nodes consist of the Huffman encoding. The Huffman encoding algorithm can be achieved only by using a one-dimensional in this paper, so the completion of the encoding doesn't depend on any computer language. The simulation results show that three one-dimension arrays can realize the Huffman encoding of any event.

Key words：Huffman coding; intermediate node; code word; Leaf node

中图分类号：TP 391

文献标识码：A

DOI:10.3969/j.issn.2095-7386.2016.01.019

文章编号：2095-7386(2016)01-0088-04

基金项目：国家自然科学基金资助项目(61179032).

作者简介：王防修(1973-)，男，副教授，E-mail: wfx323@126.com.

收稿日期：2015-12-16.