群体性事件中恐慌情绪的信息量化集结分析研究
李 静
群体性事件中恐慌情绪的信息量化集结分析研究
李静
摘要:通过对群体性事件演化过程中征兆期、爆发期、延续期、痊愈期的研究,遵循其演化过程中的规律并构建信息量化集结模型。从信息挖掘的角度,采用人工智能算法(PGSA)对群体性事件的演化、参与主体的感知以及舆情等隐秩序进行综合量化集结。通过模拟数据并分析量化集结的结果,获取相应的结论,并对群体性事件的未来发展做出合理预期,从而采取相应的措施进行预防和制止,达到最终遏制群体性事件爆发的目的。
关键词:区间数;信息量化集结模型;群体性事件;人工智能算法
群体性事件是骚乱的一种委婉表达方式,是社会群体与统治当局的冲突与对立。其常常表现为集会、游行、集体上访、集体阻断交通、罢工、罢课、罢市等形式,甚至集体围攻和冲击党政机关、重点建设工程和其他要害部位。在某些特定的情况下,群体性事件甚至可以升级为集体械斗,如打、砸、抢、烧、杀等暴力冲突,对社会的稳定及和谐具有极大的破坏力。对于一些高危群体,一旦出现以某个事件为引爆点,就可能聚集少则上百人、多则上万人的群体,从而发展为群体事件。群体性事件演化的征兆期、发作期、延续期、痊愈期,始终会受到系统内外部因素共同作用的影响[1]。尽管群体性事件具有主体多元、原因多样、爆发突然、人数众多、后果难料等复杂系统的特征,但在其演化的过程中,还是有一定的规律可循。尤其在事件发生前,往往看似表面平静如水的外部,内部却是暗流涌动。笔者从信息挖掘的角度,采用人工智能、信息挖掘、模拟仿真等信息手段,对群体性事件的演化、参与主体的感知、舆情等隐秩序进行深入研究,目的是对群体性事件进行必要的预警,为政府相关部门及时化解各种社会矛盾和冲突提供必要的理论及方法,并将其消除在萌芽阶段或减弱其发展势头,使得社会治理成本降至最低。目前,众多专家学者对群体性事件进行了深入分析研究。冯艳刚等构造了一个风险厌恶型的报童博弈模型,探讨了商品的替代率以及零售商的风险厌恶程度对最优决策的影响[2]。赵奕奕等人引入了环境噪音因子,基于有界信任规则构建了异质有界信任模型[3]。赵洪举等简化了之前的突发事件快速评估模型(SSPPM),从而快速获取应急决策者的意见和权重,简化了评估过程[4]。戴伟等人构建了基于Agent模型的非常规突发事件公共恐慌演化仿真模型,探讨了公共恐慌受政府信息发布策略的影响[5]。马妍等人提出了一种基于投影滤波的方法,可有效估计突发事件中危险源的位置[6]。宋楠等从恐怖信息传播的影响因素出发,考虑政府的最优应对策略[7]。朱建明将多目标决策用于损毁情境下的设施选址,提出了基于理想点的目标扰动最小化模型[8]。笔者构建了多属性区间数群众恐慌情绪的信息量化集结模型,对群体性事件征兆期的肇事者的情绪进行量化分析,然后运用植物模拟生长算法对群体的综合情绪进行集结。通过对集结后的群体综合情绪进行评估,为政府及相关部门化解各种社会矛盾和冲突提供依据和参考,最终遏制群体性事件爆发或者减少群体性事件危害。
一、信息量化集结模型
群体性事件征兆期的主要特征是信息传播以及群体愤怒等情绪的短期急剧上扬。当这种情绪受到煽动或者积聚到一定程度时就会造成群体性事件的爆发,对社会秩序造成威胁。引起群体性事件爆发的情绪主要有愤怒、恐慌、抑郁等,这些不良情绪在短时间内得不到宣泄便会急剧爆发并对社会秩序造成恶劣后果。因此,建立信息量化模型,通过构造多属性区间数模型将群体情绪进行量化分析。
(一)多属性区间数量化集结模型的建立及评价
群体性事件评价主要是通过集结引起群体性事件爆发的各种情绪从而对群体的总体心理有认知和了解,从而采取相应措施来进行预防和遏制。选取的群体情绪主要包括不满、抑郁、恐慌及愤怒。通过实际调研的方式了解各个群体中个体成员的这几种情绪,并通过多属性区间数的方式予以量化。由于被调查成员的情绪不完全确定,这里我们用区间数的形式来表示某个被调查成员的某种情绪值。笔者选取了青年学生、白领、教师、普通工人、公务员、农民几种典型的群体,群体情绪中较为常见的有不满、抑郁、恐慌及愤怒4种。实际操作中主要是通过调研或者问卷调查的方式对这几个群体中几种情绪进行实际的考量,从而确定各个成员的各种情绪值处于什么区间。通过植物模拟生长算法集结群体的综合情绪值,综合反映各个群体的情绪。通过这种方式,我们可以得到群体综合情绪的大致情况,从而为防止群体性事件的爆发提供合理建议。
数学家费马1634年提出,对平面上任意给定的点P1,P2,P3,找出另外一个点P,将P点分别与P1,P2,P3连接,使得这些点连线的总距离最小。这就是数学上的“费马问题”。
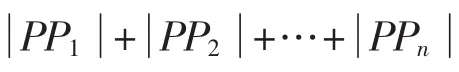
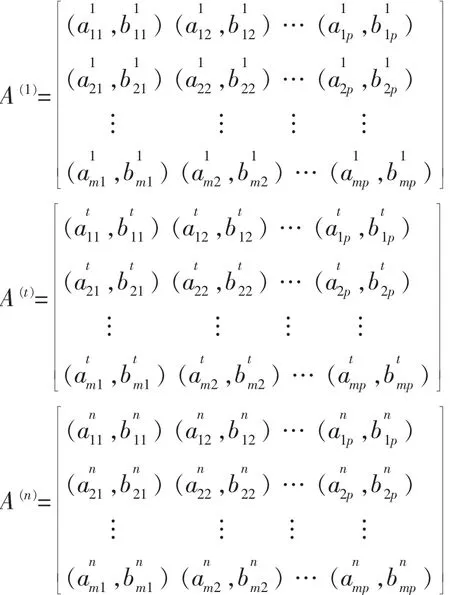
如果能够采用某种方法寻找到n个坐标点的广义费马点P,就意味着找到了n个个体的情绪的最优集结点,而该点对应的矩阵即为最优集结矩阵A*。
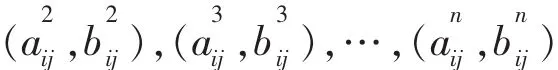
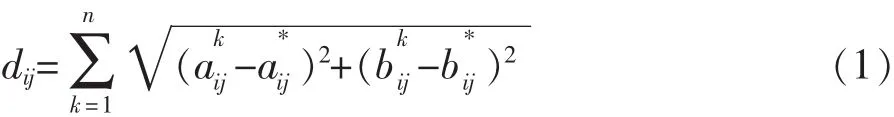
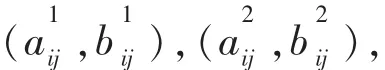
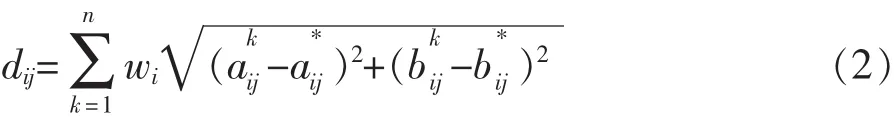
(二)基于最小欧式距离的模型构建
为了集结群情绪,建立如下优化模型,使总距离最小:
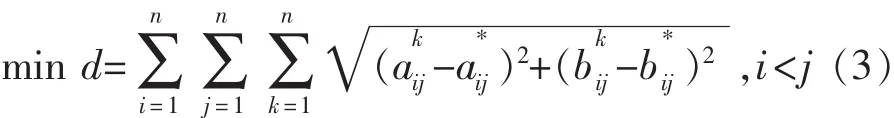
二、植物模拟生长算法集结步骤
模拟植物生长算法PGSA(Plant Growth Simulation Algorithm)是中国学者李彤教授于2005年创立的一种以植物向光性机理为启发式准则的智能优化算法[11-12]。该算法将优化问题的解空间当作植物的生长环境,将最优解当作光源,模拟真实植物的向光性机理,建立枝叶在不同光线强度环境下的快速生长演绎方式。自PGSA创立后,已引起国内外众多学者的高度关注和应用。与其他智能算法相比,PGSA算法均取得更优的结果[13-15]。K.Guney将PGSA分别与MTACO、BA、BFA这3种智能优化算法比较,PGSA得到了更加令人满意的效果,且收敛性和计算速度明显优于其他3种算法[16]。与以遗传算法(GA)、模拟退火算法(SAA)、蚁群算法(ACO)等为代表的现代启发式算法相比较,一方面,PGSA具有以枝干上形态素浓度确定的方向性特征,凸显随机平衡原理的搜索机制,能以较短的运算时间和较快的计算速度寻找到最优解;另一方面,PGSA将目标函数以及约束条件分开处理,且无需编码和解码,不仅无须构造新的计算用目标函数,增强解的稳定性,而且对参数设置的依赖性较低[17-18]。
当模拟植物生长算法是以问题所要研究的全部空间范围充当植物的生长领域时,太阳所照射的点就被视为全局最优。植物的寻优路径是沿着光源照射的方向一路向着光源生长,理论上当植物延伸到光源的位置,植物就停止了生长。可以这么认为,光相当于植物的引导员。在不同光强度的照射下,植物受到照射所产生的形态素浓度不同,这会使植物的走势发生变化。据此,笔者建立植物生长模型:假设M表示枝干长度,树干上存在的T个发芽点为SM= (SM1,SM2,…,SMT),各个发芽点的形态素浓度的数值表达式可以表示为PM=(PM1,PM2,…,PMT);设枝干的单位长度为m(m<M),其上有r个发芽点为Sm=(sm1,sm2,…,smr),每个发芽点的形态素浓度为Pm=(pm1,pm2,…,pmr)。如上所述,这两部分的发芽点形态素浓度是:
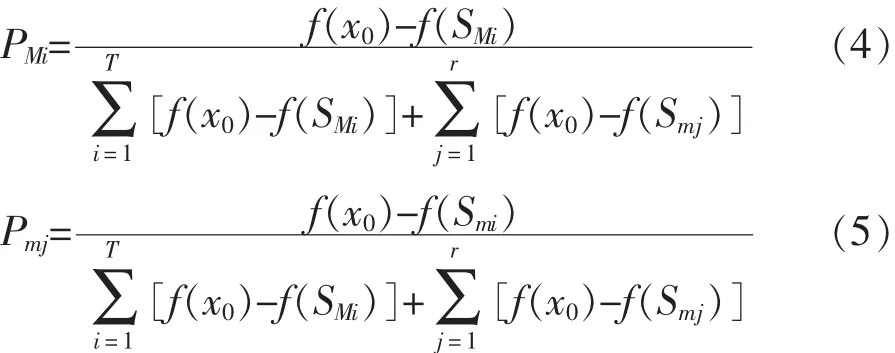
式(4)和式(5)中,x0为随机出现在可行域上的点;f函数是发芽点的背光函数。光强越弱,f函数越大。根据式(4)和式(5)可以得出:一株植物上全部的发芽点形态素浓度和是1,即

茎与枝上一共包含K+1个发芽点,即(x1,x2,…,xK+1),由式(4)和式(5)得每个发芽点的形态素浓度分别为(p1,p2,…,pK+1)。根据算法的随机性过程,随机生成一个[0,1]区间的值,以此用来作为下一次生长的新发芽点。这就好比在[0,1]之内投小球,小球接触到的区域内的发芽点即为下一次发芽枝干的新发芽点。T和r的值是随着植物向光延伸而发生改变的,刚生出的发芽点将被加入到所有现有的发芽点中,不断重复该步骤,一直到停止生长。
三、数据模拟分析
笔者拟通过对群体性事件中6个不同群体的不满、抑郁、恐慌及愤怒情绪进行模拟数据分析和集结,最终通过层次单排序得出集结后的群体情绪中各种情绪的权重。借助对群体情绪的判断,可以得出当前群体情绪大致处于什么状况,从而为有效预防和遏制群体性事件爆发提供一种量化集结分析的方法。模拟6组群体调查者的区间数多属性矩阵如下:A(1)、A(2)、A(3)、A(4)、A(5)和A(6)依次为青年学生、白领、教师、普通工人、公务员、农民群体的区间数矩阵;矩阵中从上到下依次为调查者的不满、抑郁、恐慌及愤怒四种情绪,从左到右依次为青年学生、白领、教师、普通工人、公务员、农民群体。笔者得到以下矩阵:
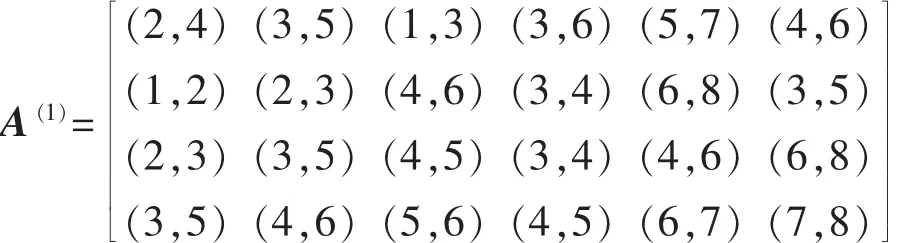

植物模拟生长算法集结后的矩阵为:

平均后得:

运用层次单排序求出:

由上述集结结果得到群体中不满、抑郁、恐慌及愤怒情绪的比重:23%处于不满情绪;27%处于抑郁情绪;21%处于恐慌情绪;29%处于愤怒情绪。综合来看,各个群体中的抑郁和愤怒情绪占据大部分。由于群体中4种情绪的人群比重较为均衡,抑郁和愤怒情绪的人群比重稍多,所以这个时候应该采取积极的疏导措施,同时为预防群体性事件爆发做出一些基础准备。
四、结论
群体性事件的爆发严重扰乱社会的正常秩序,对群体情绪的正确认知和疏导一直是让决策者头疼的问题。笔者基于多属性区间数矩阵构建了群体性事件信息集结模型并进行了模拟分析,首先通过对有负面情绪的群体进行实际调查,从而获取相关人员的负面情绪反馈,再把几种典型情绪转化成区间数判断矩阵的方式加以具体量化。最后通过植物模拟生长算法对群体负面情绪进行集结,得出群体中的情绪比重。通过这样的调查和反馈,最终为决策者提供建议和意见,以达到遏制群体性事件爆发的目的。
参考文献:
[1]FINK S.Crisis Management:Planning for The Inevitable[M].Network:Network median Management Association,1986.
[2]冯艳刚,吴军.突发事件环境下风险厌恶型报童博弈模型[J].系统工程理论与实践,2015(3).
[3]赵奕奕,彭怡,肖磊,李玲.突发事件下群体抢购行为的舆论传播机理研究[J].系统工程理论与实践,2015(3).
[4]赵洪举,彭怡,李健,朱征.突发事件快速评估模型[J].系统工程理论与实践,2015(3).
[5]戴伟,余乐安,汤铃,沈焱.非常规突发事件公共恐慌的政府信息公布策略研究:基于Multi-Agent模型[J].系统工程理论与实践,2015(3).
[6]马妍,赵玉新,陈立娟,常帅.基于投影滤波的突发事件危险源位置估计问题研究[J].系统工程理论与实践,2015(3).
[7]宋楠,付举磊,鲍勤,乔晗.基于无标度网络的恐怖信息传播与最优应对策略[J].系统工程理论与实践,2015(3).
[8]朱建明.损毁情景下应急设施选址的多目标决策方法[J].系统工程理论与实践,2015(3).
[9]堵丁柱.谈谈斯坦纳树[J].数学通报,1995(1).
[10]肖翰珅.关于广义Fermat点唯一性的探讨[J].数学通报,2012 (10).
[11]李彤,王春峰,王文波,宿伟玲.求解整数规划的一种仿生类全局优化算法:模拟植物生长算法[J].系统工程理论与实践,2005(1).
[12]李彤,宿伟玲,李磊.单级与二级整数规划算法原理及应用[M].北京:科学出版社,2007(7).
[13]丁雪枫,马良,丁雪松.基于模拟植物生长算法的易腐物品物流中心选址[J].系统工程,2009(2).
[14]李彤,王众托.模拟植物生长算法在设施选址问题中的应用[J].系统工程理论与实践,2008(12).
[15]杨磊,刘义保,刘玉娟.基于模拟植物生长算法的钴源源棒的排列优化[J].核技术,2009(12).
[16]GUNEY K,DURMUS A,BASBUG S.A Plant Growth Simulation Algorithm for Pattern Nulling of Linear Antenna Arrays by Amplitude Control[J].Progress In Electromagnetics Research,2009(17).
[17]RAO R S,NARASIMHAM S.Optimal Capacitor Placement in a Radial Distribution System Using Plant Growth Simulation Algorithm[J].Journal of Electrical Power and Energy and Energy Systems Engineering,2008(2).
[18]THIRUVENKADAMS,NIRMALKUMARA,SAKTHIVEL A.Energy Management of Large Distribution Network With Plant Growth Simulation Algorithm and Heuristic Fuzzy[J].International Journal on Electronic & Electrical Engineering,2009(1).
(编辑:唐龙)
基金项目:江苏省2015年普通高校研究生科研创新计划项目“群体性事件隐秩序的信息挖掘及其预警研究”(KYZZ15_0309)。
收稿日期:2015-12-28
作者简介:李静(1992-),男,江南大学(江苏无锡214122)管理科学与工程系2014级硕士研究生,研究方向为决策理论与方法。
中图分类号:F062.5
文献标识码:A
文章编号:1673-1999(2016)03-0042-04

