多模态RM不稳定性对初始扰动条件的依赖性分析*
王 涛,陶 钢,柏劲松,李 平,汪 兵,杜 磊
(1.南京理工大学能源与动力工程学院,江苏南京 210094;2.中国工程物理研究院流体物理研究所,四川绵阳 621999)
界面不稳定性,包括涉及冲击驱动的Richtmyer-Meshkov(RM)不稳定性[1-2]、惯性力驱动的Rayleigh-Tayloy(RT)不稳定性[3-4]以及剪切驱动的Kelvin-Helmholtz(KH)不稳定性[5],是我们在自然界和工程应用中经常遇到的一类物理现象,比如天体物理中的超新星爆发、惯性约束聚变、磁约束聚变、核武器爆炸、超音速燃烧系统等。界面不稳定性及其诱发的湍流混合作为流体动力学领域的重要和前沿课题,一直以来受到流体力学工作者,特别是各国武器实验室的格外关注。在实际问题中,各类界面不稳定性经常是共存的,使该问题的研究变得更复杂。
众所周知,界面不稳定性的发展受初始扰动条件影响很大,前人也多次对界面不稳定性发展受初始扰动的影响进行过分析和研究。比如,在RM不稳定性方面,Thornber等人[6]通过一系列精确控制的数值实验,研究了无反射冲击情况下三维多模态初始扰动条件对混合区增长率的影响,结果显示,混合区的增长强烈地依赖于初始条件。Schilling等人[7]证实,从初始冲击后至反射冲击前,混合区宽度对初始扰动振幅很敏感。Leinov等人[8]研究显示,反射冲击波再加载后,混合区的演化与反射冲击波到达时的界面振幅无关,但是与反射冲击波的强度有关。Balasubramanian等人[9]的实验显示,初始扰动波长和振幅对反射冲击后气帘不稳定性混合有影响。Bai等人[10]关于初始流场非均匀性对扰动增长影响的研究表明,在反射冲击波再加载之前的线性和弱非线性阶段,初始流场非均匀性对不稳定性的演化具有相当大的影响;而在再加载之后的强非线性阶段,非均匀性效应急剧衰减。王涛等人[11]也分析研究了无反射冲击波作用下单模态RM不稳定性发展受初始扰动的影响,结果表明,扰动增长对初始条件有很强的依赖性。但是,反射冲击波作用后混合区发展受初始扰动的影响作用还不是很明确,需要进一步深入开展相关研究。本研究通过大涡数值模拟方法,研究多次冲击作用下三维多模态RM不稳定性发展对初始扰动条件的依赖性。
2 计算方法
数值模拟采用自研的可压缩多介质黏性流动和湍流大涡(Multi-Viscous-Flow and Turbulence,MVFT)模拟程序[12-13]。该大涡模拟的流场控制方程为经过Favre滤波后的可压缩多介质黏性流动Navier-Stokes方程组
(1)

(2)
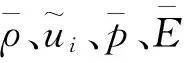
采用算子分裂技术将方程组(1)式描述的物理过程分解为3个子过程进行计算,即整个通量计算分解为无黏通量、黏性通量和热通量计算3部分。无黏通量的计算采用多介质的高精度分段抛物线方法(Piecewise Parabolic Method,PPM),两步Lagrange-Remapping型的PPM方法分以下4个步骤进行:(1) 物理量分段抛物插值;(2) 近似Riemann问题求解;(3) Lagrange方程组推进求解;(4) 将物理量映射到静止的欧拉网格上。然后在无黏通量的基础上,采用二阶空间中心差分方法和两步Runge-Kutta时间推进方法求解黏性通量、热通量及标量输运通量。详细的数值方法参考文献[15-16]。
3 结果分析
计算模型来自Erez等人[17]开展的RM不稳定性激波管实验。激波管测试段长度为180 mm,内截面尺寸为80 mm×80 mm。实验气体为空气和六氟化硫(SF6),初始计算参数列于表1。

表1 气体初始参数Table 1 Initial properties of air and SF6
计算模型如图1所示。马赫数为1.2的冲击波加速空气/六氟化硫(Air/SF6)界面。计算域大小为[-60 mm,180 mm]×[0 mm,80 mm]×[0 mm,80 mm],离散网格数为768×256×256,网格大小为0.312 5 mm,采用6×2×2个CPU进行并行计算。多模态初始扰动通过8个正弦模态叠加而成
(3)

计算中,初始扰动主模态的横向波长为0.80、1.00、1.25、1.60、2.00、2.50、3.20、4.00 mm。为了分析初始扰动条件对RM不稳定性及湍流混合发展的影响,我们通过改变初始扰动的振幅来改变初始扰动强度。初始扰动强度(PS)定义为初始扰动振幅和波长之比,对于多模态初始扰动,PS=η0/λ,其中λ≈2 mm为平均波长。模型的初始参数列于表2。
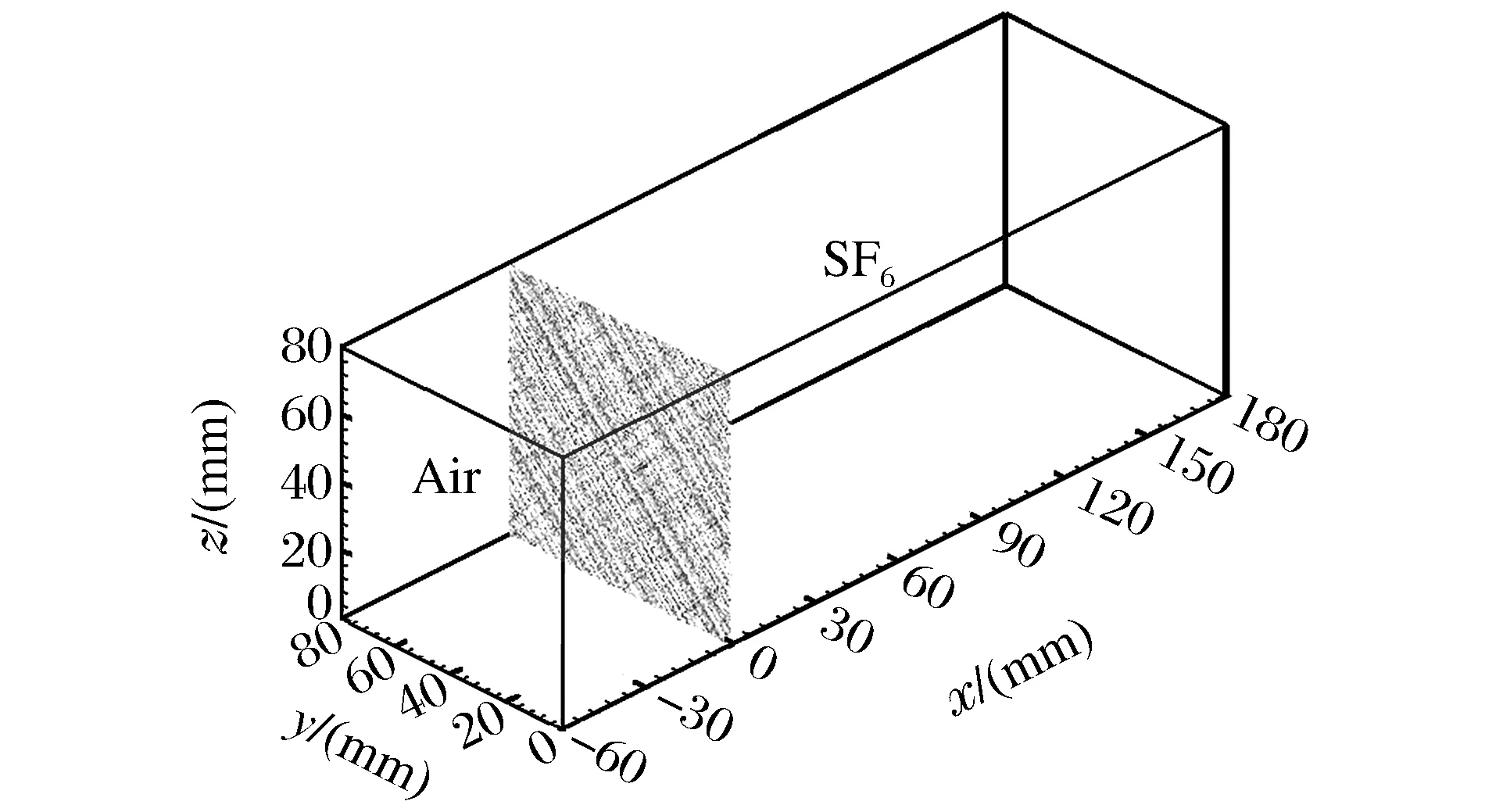
图1 计算模型Fig.1 Computation model

Caseη0/(mm)PS10.070.03520.140.07030.280.14040.560.28051.120.560
冲击波加速空气/SF6扰动界面,向SF6气体中产生一个透射冲击波。该透射冲击波从激波管尾端反射回来再次冲击界面时(tres),向SF6气体中反射一个稀疏波。反射稀疏波从激波管尾端反射回来和界面相互作用(texp1)后又向SF6气体中反射一个压缩波,当这个压缩波再反射回来和界面相互作用时(tcom1),又向SF6气体中反射一个稀疏波。这样的一系列压缩波和稀疏波交替在测试段中运动,并和界面相互作用,形成对界面的多次冲击,但是每次冲击作用后,能量的转移使波的强度进一步降低,长时间后对湍流混合区的演化难以产生影响。

图2 湍流混合区定义Fig.2 Definition of turbulent mixing zone
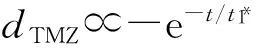
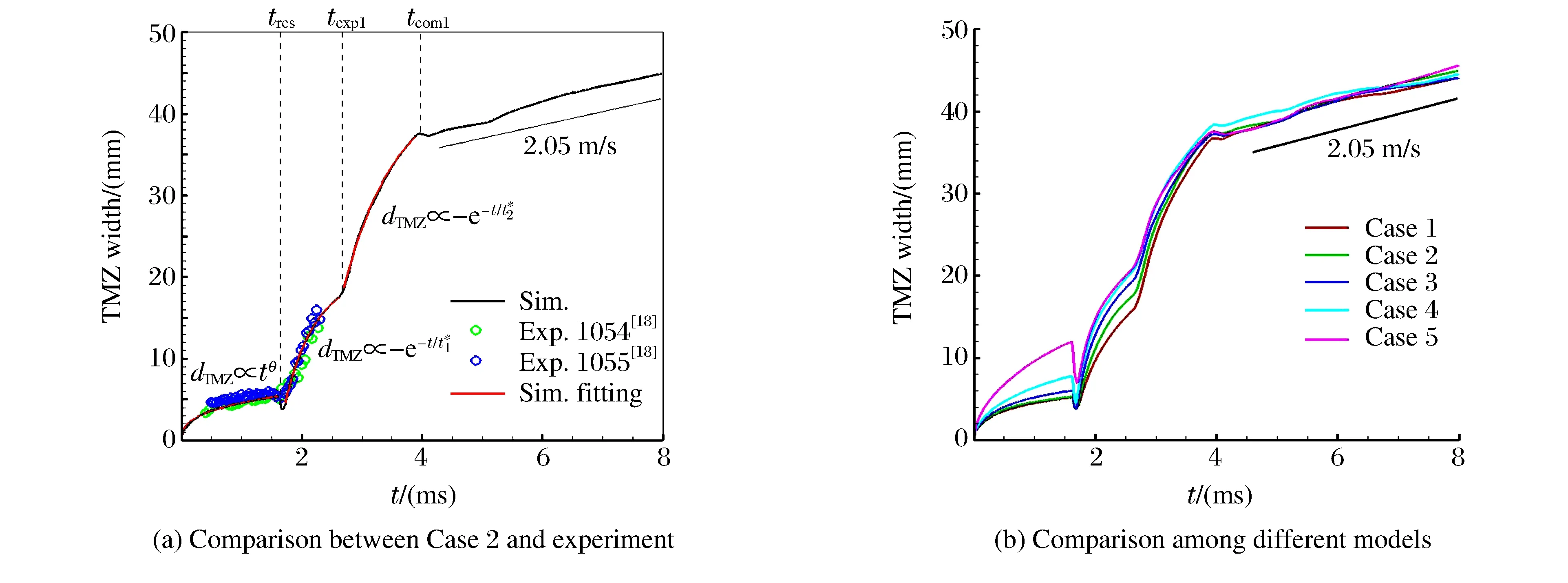
图3 不同模型湍流混合区宽度随时间的增长历史Fig.3 Time histories of growth of TMZ width (dTMZ) of different models
图3(b)给出了不同模型的湍流混合区宽度的增长历史。可以看出,初始扰动强度大,对应的湍流混合区宽度较大,相应的增长速率也较高,这主要体现在初始冲击后至反射冲击前和反射冲击后至第一次反射稀疏波作用前两个阶段。而反射稀疏波作用后,初始扰动对湍流混合区宽度增长的影响逐渐减弱,直至反射压缩波作用后,湍流混合区的增长基本不受初始扰动的影响,以基本一致的线性规律增长,增长速度为2.05 m/s,即在第一次反射稀疏波作用后,湍流混合区的发展逐渐失去对初始扰动条件的记忆。表3列出了不同模型在初始冲击后、反射冲击后以及第一次反射稀疏波作用后湍流混合区宽度的增长因子。图4是不同时刻Case 1模型中,SF6的体积分数为0.1和0.9的等值面所显示的湍流混合区图像,表明混合区具有复杂的空间结构。

表3 不同模型湍流混合区宽度的增长因子Table 3 Growth factors of TMZ width of different models

图4 SF6的体积分数为0.1和0.9的等值面所显示的不同时刻湍流混合区图像Fig.4 Images of TMZ visualized by the volume fraction isosurface of 0.1 and 0.9 for SF6 at different times
下面我们通过比较湍流混合区的统计量进一步分析初始扰动条件的影响。统计量包括湍动能k、湍动能耗散率ε和拟涡能Ω
(4)
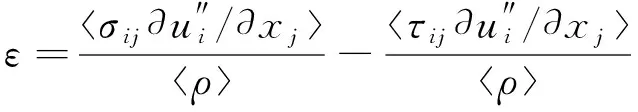
(5)

(6)
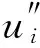
图5~图7分别给出了不同模型湍流混合区的湍动能峰值、湍动能耗散率峰值及拟涡能峰值随时间变化的历史。可以看出:当界面受到波的冲击作用时,冲击波携带的能量通过斜压作用沉积到界面上,促使界面快速发展,此刻混合区统计量也随之急速增大;之后由于波的冲击作用消失,统计量在耗散和扩散作用下逐渐衰减。初始冲击后,湍动能和拟涡能以幂次律衰减,而湍动能耗散率以指数规律衰减;反射冲击后,湍动能、湍动能耗散率和拟涡能均以指数规律衰减;反射稀疏波作用后,这些统计量也以指数规率衰减,但是衰减因子不同;其后,由于波的强度太小,没有足够的能量沉积,所以统计量以渐近方式衰减。
湍动能、湍动能耗散率及拟涡能都随着初始扰动强度的增大而增大,也就是说,在相同强度冲击波作用下,较大的初始扰动会导致更强的湍流脉动,湍动能的传输更快,湍动能耗散也更快,产生的斜压涡量场也更强。在初始冲击后至反射冲击前和反射冲击后至反射稀疏波作用这两个阶段,受初始扰动的影响较大。第一次反射稀疏波作用后,湍流混合区的发展基本不受初始扰动条件的影响。

图5 不同模型湍流混合区湍动能峰值时间历史Fig.5 Time history of turbulent kinetic energy of different models in TMZ
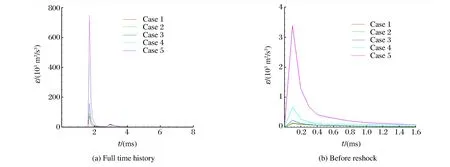
图6 不同模型湍流混合区湍动能耗散率峰值时间历史Fig.6 Time histories of turbulent kinetic energy dissipation rate of different models in TMZ
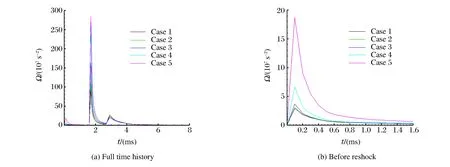
图7 不同模型湍流混合区拟涡能峰值时间历史Fig.7 Time histories of enstrophy of different models in TMZ
4 结 论
利用发展的适用于可压缩多介质黏性流动和湍流大涡模拟的程序MVFT,对轻/重气体(空气/SF6)界面构型下多次冲击作用的三维多模态RM不稳定性发展及其对初始扰动条件的依赖性进行了数值模拟。研究结果显示,初始冲击后,湍流混合区宽度以幂次律增长;反射冲击后和第一次反射稀疏波作用后,湍流混合区宽度以指数规律增长,但其增长因子不同;第一次反射压缩波作用后,近似以线性规律增长。而湍流混合区统计量则以相似的规律衰减。多模态RM不稳定性发展对初始扰动条件有很强的依赖性,主要体现在初始冲击后至反射冲击前和反射冲击后至第一次反射稀疏波作用前两个阶段,而在第一次反射稀疏波与界面作用后,湍流混合区的发展逐渐失去对初始扰动条件的记忆。
[1] RICHTMYER R D.Taylor instability in shock acceleration of compressible fluids [J].Commun Pure Appl Math,1960,13(2):297-319.
[2] MESHKOV E E.Instability of the interface of two gases accelerated by a shock wave [J].Sov Fluid Dyn,1969,4(5):101-104.
[3] RAYLEIGH LORD.Scientific papers Ⅱ [M].Cambridge:Cambridge University Press,1900:200.
[4] TAYLOR G I.The instability of liquid surfaces when accelerated in a direction perpendicular to their plane [J].Proc R Soc London (Ser A),1950,201:192.
[5] CHANDRASEKHAR S.Hydrodynamic and hydromagnetic stability [M].London:Oxford University Press,1961.
[6] THORNBER B,DRIKAKIS D,YOUNGS D L,et al.The influence of initial conditions on turbulent mixing due to Richtmyer-Meshkov instability [J].J Fluid Mech,2010,654:99-139.
[7] SCHILLING O,LATINI M.High-order WENO simulations of three-dimensional reshocked Richtmyer-Meshkov instability to late times:dynamics,dependence on initial conditions,and comparisons to experimental data [J].Acta Math Sci,2010,30(2):595-620.
[8] LEINOV E,MALAMUD G,ELBAZ Y,et al.Experimental and numerical investigation of the Richtmyer-Meshkov instability under re-shock conditions [J].J Fluid Mech,2009,626:449-475.
[9] BALASUBRAMANIAN S,ORLICZ G C,PRESTRIDGE K P,et al.Experimental study of initial condition dependence on Richtmyer-Meshkov instability in the presence of reshock [J].Phys Fluids,2012,24(3):034103.
[10] BAI J S,WANG B,WANG T,et al.Numerical simulation of the Richtmyer-Meshkov instability in initially nonuniform flows and mixing with reshock [J].Phys Rev E,2012,86(6):066319.
[11] 王 涛,柏劲松,李 平,等.单模态RM不稳定性的二维和三维数值计算研究 [J].高压物理学报,2013,27(2):277-286.(in English)
WANG T,BAI J S,LI P,et al.Two and three dimensional numerical investigations of the single-mode Richtmyer-Meshkov instability [J].Chinese Journal of High Pressure Physics,2013,27(2):277-286.
[12] WANG T,BAI J S,LI P,et al.Large-eddy simulations of the Richtmyer-Meshkov instability of rectangular interface accelerated by shock waves [J].Sci China Ser G,2010,53(5):905-914.
[13] BAI J S,LIU J H,WANG T,et al.Investigation of the Richtmyer-Meshkov instability with double perturbation interface in nonuniform flows [J].Phys Rev E,2010,81(2):056302.
[14] VREMAN A W.An eddy-viscosity subgrid-scale model for turbulent shear flow:algebraic theory and applications [J].Phys Fluids,2004,16(10):3670-3681.
[15] WANG T,BAI J S,LI P,et al.The numerical study of shock-induced hydrodynamic instability and mixing [J].Chin Phys B,2009,18(3):1127-1135.
[16] BAI J S,WANG T,LI P,et al.Numerical simulation of the hydrodynamic instability experiments and flow mixing [J].Sci China Ser G,2009,52(12):2027-2040.
[17] EREZ L,SADOT O,ORON D,et al.Study of the membrane effect on turbulent mixing measurements in shock tubes [J].Shock Waves,2000,10:241-251.
[18] SREBRO Y,ELBAZ Y,SADOT O,et al.A general buoyancy-drag model for the evolution of the Rayleigh-Taylor and Richtmyer-Meshkov instabilities [J].Laser Part Beams,2003,21:347-353.
[19] WANG T,BAI J S,LI P,et al.Large-eddy simulation of the multi-mode Richtmyer-Meshkov instability and turbulent mixing under reshock [J].High Energy Density Physics,2016,19:65-75.

