分体式动能子弹对混凝土靶的侵彻与毁伤特性分析*

韩 晶，王 华，陈智刚

(1.中北大学机电工程学院，山西太原 030051；2.北京航空航天大学宇航学院，北京 100191)

随着国防科技的发展，高价值军事目标防护体系日趋地下化和坚固化，对常规钻地武器提出了更高的要求。为了应对这一发展趋势，各国在发展整体式动能侵彻战斗部和串联式复合侵彻战斗部的同时，正加紧新型原理钻地弹药的研究[1-3]。以“深度挖掘者”为例，该主动式钻地武器借鉴了天然气与石油开采中的“干钻”与“风钻”技术，实现了多管小口径火炮技术和常规钻地弹药的有机结合。其具体的工作原理和作用过程如图1所示[4-5]：当“深度挖掘者”在目标区上方经载机投放后，首先由降落伞减速调姿；然后，在下降过程中适时开启弹载火炮发射系统，交替发射小口径动能碎石弹及爆破弹，分别实现对岩土介质的持续预裂破碎及后向抛掷，使其形成一定尺寸的钻地通道；最后，主战斗部随进起爆。在主动侵彻过程中，动能碎石弹如何借助于一定的发射速度和结构形式实现对岩土介质的高效破碎，是探索研究主动式钻地原理的关键之一。

常规结构弹对于岩土目标的破碎效果有限，无法满足实际需求。鉴于此，早在20世纪70年代，为实现井下硬岩巷道的快速化掘进，同时考虑工业使用成本，国外采用了内部为混凝土弹芯、外部为金属弹壳的结构，其工作原理与横向效应增强型弹类似。之后，相关研究人员又将普通混凝土弹芯替换为高强度钢纤维混凝土材料，以提高弹丸的结构强度[6-7]。然而，一方面，混凝土材料自身强度较低，无法满足高速发射的要求；另一方面，由于小口径碎石弹空间尺寸的限制，钢纤维混凝土弹芯难以直接推广至该结构方案的设计中。因此，为实现主动侵彻子弹的功能需求，提出一种分体式动能子弹结构。通过数值仿真与靶场实验相结合的方法，分析其侵彻特性，并运用分形几何理论方法对该子弹对素混凝土靶的毁伤破碎度进行定量描述，以期为评价分体式动能子弹对混凝土的毁伤效果提供参考。

2 分体式动能子弹结构方案

为提高动能子弹的毁伤效果，Pickard等人[8]提出了“花瓣盛开式”的侵彻方式，其原理如下：当子弹作用于目标介质时，由于弹丸高速旋转，在离心力作用下，弹丸逐步沿预制刻槽径向分解形成若干破片，其变形过程类似于花瓣的绽放。根据该侵彻原理，并考虑到岩土类硬目标介质的特点和弹道飞行稳定性，提出了一种分体式碎石弹设计方案。如图2(a)所示，分体式动能子弹由采用锥形弹头的主侵彻体、缓冲元件和辅助侵彻体等部分组成。辅助侵彻体的周向均匀预制了4段断裂槽，整体通过螺纹与主侵彻体固定连接，高分子缓冲元件填充于辅助侵彻体中。弹丸直径为23 mm，主、辅侵彻体的长度分别为36.0和41.5 mm，头部锥角为20°。该子弹的作用原理如图2(b)所示，当弹丸高速撞击目标时，主侵彻体率先侵入靶内，使靶体形成空腔和大量的径向裂隙区；随后，受高速离心作用的辅助侵彻体沿径向预制刻槽分解，断裂破片对目标进行二次侵彻冲击；一旦主侵彻体和辅助侵彻体导致的径向裂纹相互交错贯通之后，就会使破碎介质从靶体上剥离。

图2 分体式动能弹结构与作用原理Fig.2 Structure and mechanism of split kinetic energy projectile

3 数值仿真分析

3.1 仿真模型

图3 计算模型Fig.3 Calculation model

为实现对分体式动能子弹侵彻混凝土的数值模拟，建立弹靶系统的有限元计算模型，如图3所示。由于弹丸着靶后弹托和弹带等零件已脱落，因此建模时未予以考虑。仿真软件采用AUTODYN，弹体采用SPH(Smoothed Particle Hydrodynamics)模拟，粒子半径均为1 mm。混凝土靶为400 mm×400 mm×300 mm的立方体，采用Lagrange法划分单元，靶体模型外表面上，节点的运动自由度为零，网格大小为4 mm，单元数量为14 794。为减少边界效应影响，设靶体边界满足无应力反射条件。

3.2 材料模型

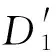
表1 弹体的材料参数Table 1 Material parameters of projectile

表2 混凝土靶材料参数Table 2 Material parameters of concrete target

3.3 仿真结果

当弹丸的入射速度为400 m/s，旋转角速度为1 600 r/s时，分体式动能子弹垂直侵彻混凝土的弹靶响应历程如图4所示。图4(a)给出了弹丸的变形过程，中心部分为主侵彻体，周边为辅助侵彻体。在0.32 ms时，在轴向过载和离心力的共同作用下，在头部径向弯卷变形的同时，辅助侵彻体沿各预制切断槽产生扭转断裂失效破坏，由于惯性，各破片的姿态不同，存在一定侵彻攻角；当0.80 ms时，各破片径向散布距离进一步增加。图4(b)为靶体损伤的变化。可以看出：0.24 ms时，主侵彻体着靶后，混凝土靶上出现了以弹丸侵彻点为中心的破碎圈和径向裂隙区；0.32 ms时，在主、辅侵彻体共同作用下，靶体内的破碎区和裂纹沿靶体径向进一步扩展。对于方形靶体，由于应力集中效应，对角线方向上的裂纹扩展速度最快。由于模拟半无限靶，因此产生的裂隙并未完全贯通。

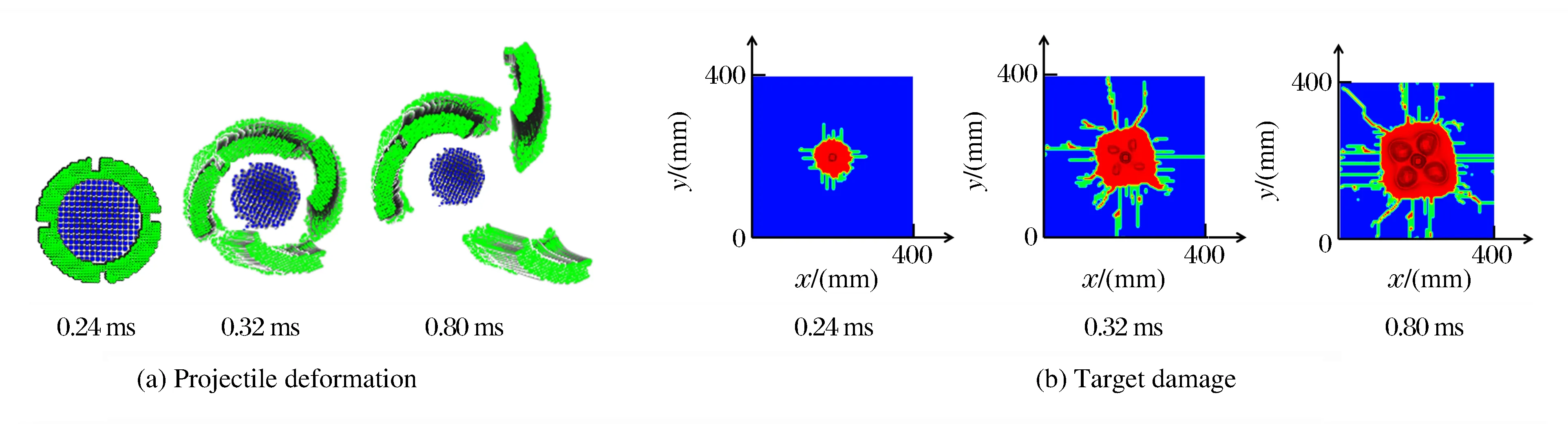
图4 弹靶响应历程Fig.4 Response process of projectile and target

图5为侵彻过程中分体式弹丸主、辅侵彻体的响应变化曲线。由图5(a)可知，主侵彻体和辅助侵彻体的着靶速度均由400 m/s减小为零，受质量、结构形状等因素的影响，相对于主侵彻体，辅助侵彻体的速度变化率更大。由图5(b)可知，辅助侵彻体的峰值过载比主侵彻体高43%。由图5(c)可知，当侵彻过程结束时，主侵彻体和辅侵彻体的位移分别为80.4和34.2 mm，即主侵彻体的侵彻深度是辅助侵彻体的1.4倍。另外，由于主、辅侵彻体先后进入靶体，在靶体内形成的冲击应力波相互叠加，使得过载曲线波动较大，与之前弹丸过载特征不同。对图5(b)中过载曲线进行快速傅里叶变换得到图5(d)，可以看出，冲击应力波叠加形成的振动冲击波频率主要集中在67 Hz附近。

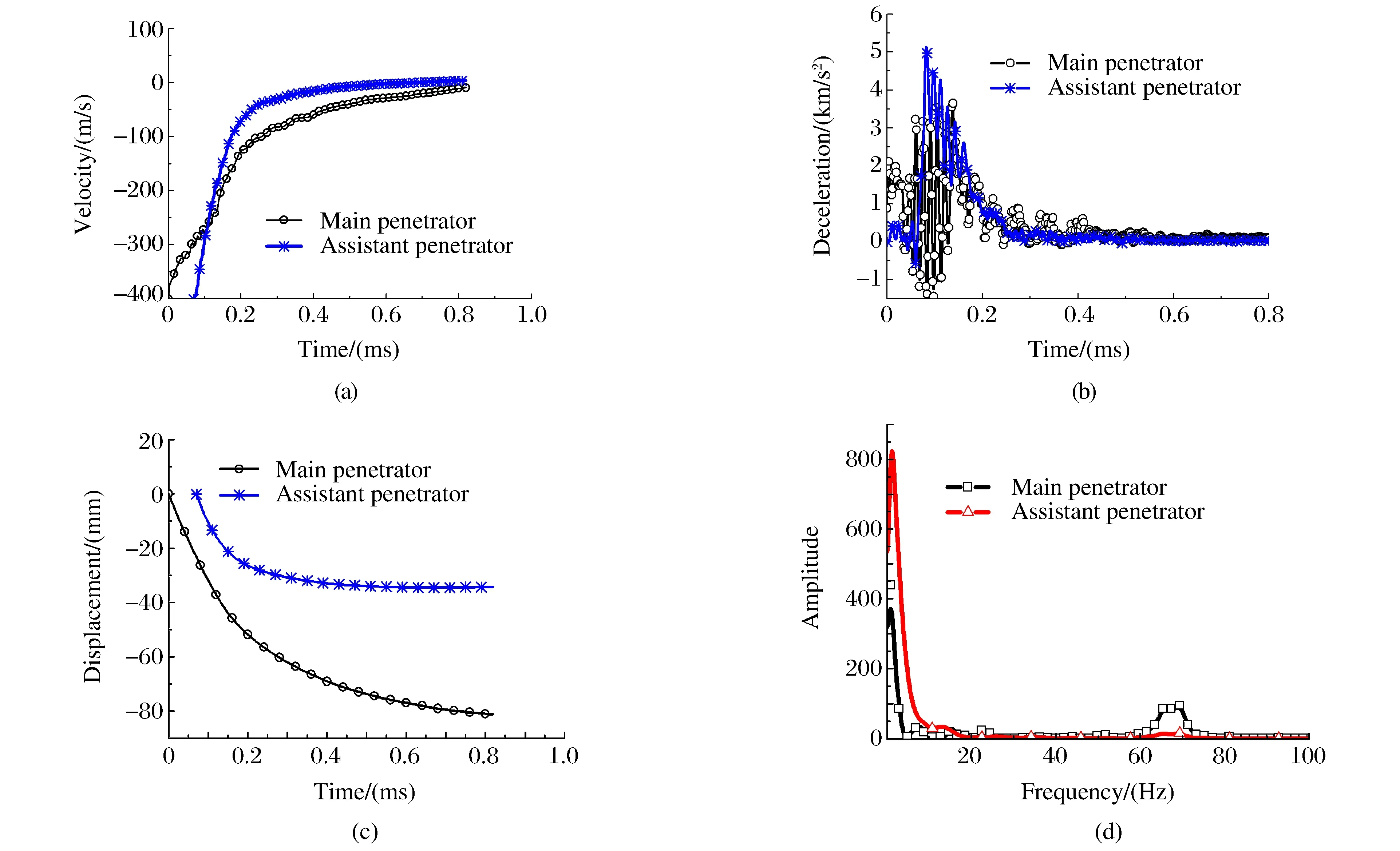
图5 弹丸侵彻响应曲线Fig.5 Response curves of projectile penetration

4 侵彻实验

4.1 实验布局

通过靶场实验可以研究该动能子弹对素混凝土靶的毁伤特性。实验中所用动能弹和素混凝土靶如图6所示，子弹质量为180 g，靶体直径为500 mm，厚度为400 mm，实验靶体外部采用2 mm厚铁皮箍紧。混凝土的单轴平均抗压强度为35 MPa，卵石骨料大小均匀，平均直径约为8 mm。采用∅23 mm火炮进行正侵彻加载，利用靶网测试着靶速度。同时，为有效搜集侵彻过程中产生的混凝土碎块，在混凝土靶的正面铺设4 m×4 m的白色条幅。

图6 靶场实验用弹及混凝土靶Fig.6 Actual projectile and concrete target used in experiment

4.2 实验结果

动能弹侵彻后，部分靶体的破坏情况如图7所示。由图7可知，侵彻结束后，主侵彻体仍较为完整，其变形及表面质量侵蚀较小，而辅助侵彻体分解形成的破片头部存在明显的弯卷变形，部分甚至发生了整体断裂，该现象与仿真结果较为吻合。另外，由于辅助侵彻体分解形成的各破片同时受到旋转惯性、重力、侵彻姿态及混凝土材料的非均质性等因素的影响，因此，当侵彻结束时，部分破片与靶体脱离。

图7 弹靶破坏情况Fig.7 Damage of projectiles and target

通常弹坑直径、弹坑深度与弹丸的着靶速度和直径成一定的比例。对于混凝土介质，当弹速小于500 m/s时，成坑半径约为弹体直径的2倍，成坑范围约为弹径的4～6倍[9]。表3给出了分体式动能子弹侵彻混凝土靶的实验结果，其中v为弹体着靶速度，d和hc分别为成坑直径和深度，V为成坑体积，hmain和hassistant分别为主侵彻体和辅助侵彻体的侵彻深度，n为脱落靶体的辅助侵彻体破片数。可以看出，在主侵彻体和辅助侵彻体共同作用下，混凝土厚靶的成坑直径与弹径之比均已超过10，而侵彻深度与弹径之比约为4，即横向破坏效应更明显。图8给出了混凝土靶的三维断裂仿真结果，统计得到的弹坑最大直径约为241 mm，成坑深度约为64 mm。图5中主、辅侵彻体的侵彻深度分别为80和34 mm，与实验相比，计算与实验结果的相对误差不超过10%。

表3 实验结果统计Table 3 Statistical results for experiments

除侵彻特性外，还分析了动能子弹对混凝土靶的破碎效果。将实验搜集得到碎块进行筛析称重，测量得到碎块特征长度累积率如图9所示。从图9可以看出，实验中靶体破碎块体的特征长度主要集中在30 mm以内，且随着侵彻速度的增加，特征长度小的破碎块体所占比例有所增加。

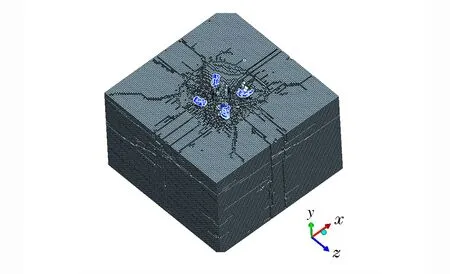
图8 混凝土靶断裂仿真结果Fig.8 Simulation result of concrete target fragmentation

图9 破碎块体特征长度的分布Fig.9 Distribution of the fragment characteristic length

依据上述统计结果可知，破碎块体的块度质量特征可近似用威布尔分布模型描述

(1)

式中：F(R)为特征尺寸小于R的破碎块体质量占碎块总质量中的比例；λ为由弹丸侵彻特征决定的破碎特征参数，根据实验拟合，弹体速度为400、417和434 m/s，λ取值分别为20.1、23.8和24.5。

4.3 破碎效应的分形描述

分形几何主要是通过分维数和无标度区间两个参数描述介质破碎过程的统计自相似特征。分维数的基本定义如下[10]

(2)

式中：D为分形维数，ε为标度，N(ε)为在标度ε下所得测量值。

定义M(R)为特征尺寸小于R的碎块累积质量，Mt为混凝土碎块的总质量。当碎块质量遵循威布尔分布时，有

(3)

式中：σ为碎块的平均特征尺寸，b为块度均匀指数。

将指数部分展开成幂级数形式，并取前两项作近似，可得到

(4)

若混凝土破碎后碎块分布具有分形特征，则由(4)式可得

(5)

对(5)式取微分，得dM∝Rb-1dR，根据质量定义dM∝R3dN，则有

(6)

由(6)式可得分维数

(7)

考虑到满足(4)式等价于M(R)/Mt与R在双对数坐标系中具有线性关系，可以得到分维数D的计算方法如下：利用筛析法称取动能子弹侵彻后的混凝土碎块质量，获得特征尺寸小于R的碎块在总质量中所占比例为M(R)/Mt，然后在双对数坐标lgR-lg[M(R)/Mt]下作图，根据曲线斜率，并结合(7)式即可得到分维数。

由图10可知，当弹体着靶速度为400、417和434 m/s时，曲线的相关系数分别为0.989、0.989和0.992，即混凝土碎块质量累积率随特征长度的分布在双对数坐标下具有较好的线性特征。该结果说明分体式动能子弹侵彻后，混凝土靶体碎块存在统计自相似性。进一步计算可得，弹体速度为400、417和434 m/s时，相应的分维数分别为1.145、1.386和1.529。由于块度分布的分维数能够定量反映分体式动能弹侵彻素混凝土靶的破碎度，因此分维数可以作为分体式动能子弹毁伤效果的评价指标。

5 结 论

通过数值仿真和靶场实验对分体式动能子弹侵彻混凝土过程进行了分析，与传统动能弹相比，分体式结构能够有效提高弹体对岩土类目标介质的横向作用范围，靶体的成坑直径与弹径之比可达10以上。分形几何理论常用于矿山岩土爆破工程领域。分体式动能子弹侵彻混凝土靶的实验研究表明，动能弹侵彻作用下混凝土介质的破碎特征符合分形几何相似理论，侵彻过程中混凝土靶体的破碎统计特征可使用分形维数描述。

[1] MAYERSAK J R.Kinetic energy cavity penetrator weapon:US10/443621 [P].2004-11-25.

[2] 梁 斌,陈小伟,姬永强,等.先进钻地弹概念弹的次口径高速深侵彻实验研究 [J].爆炸与冲击,2008,28(1):1-9.

LIANG B,CHEN X W,JI Y Q,et al.Experimental study on deep penetration reduced-scale advanced earth penetrating weapon [J].Explosion and Shock Waves,2008,28(1):1-9.

[3] 孙传杰,卢永刚,张方举,等.新型头形弹体对混凝土的侵彻 [J].爆炸与冲击,2010,30(3):269-275.

SUN C J,LU Y G,ZHANG F J,et al.Penetration of cylindrical-nose-tip projectiles into concrete targets [J].Explosion and Shock Waves,2010,30(3):269-275.

[4] HAMBILING D.Novel warhead may bust the deepest bunkers [J].New Sci,2005(2508):14-15.

[5] GOLDSTEIN Y S.Method and apparatus for penetrating hard materials:US6405628 [P].2002-06-18.

[6] CONROY P J,HEIMERL J M,FISHER E.Rapid excavation and mining (REAM) system-revisited [R].Maryland:Army Research Lab Aberdeen Proving Ground,2000.

[7] MACHINA M.Reduced energy consumption through projectile based excavation:FC26-01NT41059 [R].Alexandria:Advanced Power Technologies Inc,2003.

[8] PICKARD R K.Fragmenting bullet:US6776101 [P].2004-08-17.

[9] FORRESTAL M J,ALTMAN B S,CARGILE J D,et al.An empirical equation for penetration of ogive-nose projectiles into concrete target [J].Int J Impact Eng,1994,15:395-405.

[10] JIN X Y,LI B,TIAN Y,et al.Study on fractal characteristics of cracks and pore structure of concrete based on digital image technology [J].Res J Appl Sci,2013,5(11):3165-3171.