汇聚型超高速发射装置的发射腔计算设计*
王 宇,柏劲松,2,王 翔,2,谭 华,2,李 平
(1.中国工程物理研究院流体物理研究所,四川绵阳 621999;2.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理实验室,四川绵阳 621999)
1 引 言
超高速发射主要为超高压状态方程测量提供加载手段,以期实现对太帕(1012Pa)量级下物质的相应特性和状态方程的研究[1-2]。要达到这一目标,轻质的Al、Mg、Ti二级飞片需要发射到约16 km/s的速度方能实现,而更重的Ta、Pt二级飞片需要发射到10 km/s以上。常见的超高速发射技术有激光加载技术、Z-Pinch技术、三级炮技术等,其中三级炮技术由于实验设备简单、费用低,驱动过程中物理状态变化较小,基本满足状态方程测量的要求,因而是开展极端高压下材料状态方程测量的重要手段。
美国圣地亚实验室在20世纪90年代发展了非汇聚型超高速发射技术,能将1 mm厚的克量级铝、镁、钛合金飞片加速到10 km/s[3],将0.5 mm厚的铝、钛合金飞片加速到12.2 km/s[4],将长径比约为0.5的厚块飞片加速到10.2 km/s[5]。使用阶梯型的套筒替代原有的等直径的套筒,进一步发展了汇聚型的超高速发射装置(EHVL),能将1 mm厚的钛合金飞片加速到14.4 km/s,0.5 mm厚的钛飞片加速到15.8 km/s[6],甚至在此装置上实现了高达19 km/s的超高速发射[7],但飞片在飞行过程中已经不能保持其完整性。国内目前使用汇聚型超高速发射装置已能将0.5 mm厚的Ta飞片加速到13 km/s。更高速度的获得需要对现有的发射装置进行优化设计,由于影响二级飞片速度的因素较多,包括级轻气炮的加载能力、一级飞片和二级飞片的尺寸和结构参数、发射腔构型等因素,若完全依靠实验进行优化会产生高昂的成本,需通过数值模拟精心设计,进一步提高二级飞片的速度。
前期我们已经开展了一级飞片结构的优化设计,有效地提高了二级飞片的速度,改善了二级飞片在发射管出口处的平面性。本研究主要使用多介质流体高精度欧拉程序MFPPM对发射腔的结构进行计算设计,分析不同发射腔构型对二级飞片速度、速度差异、平面性的影响。
2 数值方法
将三阶精度PPM(Parabolic Piecewise Method)方法和VOF(Volume of Fluid)相结合,使用维数分裂方法将多维问题简化为多个一维问题来处理,实现了可压缩流体的空间多维求解。一维多介质流欧拉方程组为
(1)
式中:ρ、u、p分别表示密度、速度和压力,E表示单位质量的总能量,N表示物质的种类,Y(i)为第i种介质的体积分数,满足∑Y(i)=1。
为了有效地捕捉多介质流体交界面,运用Lagrange-Remapping算法进行求解。整个计算过程分为4个步骤完成:(1) 物理量的分段抛物插值;(2) 近似Riemann问题的求解;(3) Lagrange方程组的推进求解;(4) 最后将物理量变回到静止的Euler网格上。具体求解参考文献[5]。在上述基础上编制了具有自主知识产权的多介质流体高精度欧拉计算程序(MFPPM),并对程序进行了验证[8-9],对于二级飞片自由面速度的计算精度在1%左右,成功将其应用于超高速发射[10-11]和界面不稳定性方面的研究[12]。
3 计算设计结果
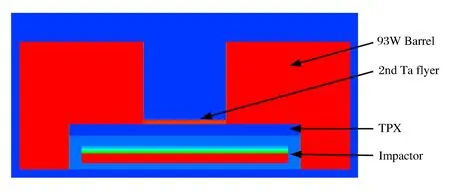
图1 汇聚型超高速发射装置示意图 Fig.1 Schematic of enhanced hypervelocity launch setup
在汇聚型超高速发射装置(图1)中,一级飞片采用93W/Cu/TC4/Al/MB2/PMMA材料体系,厚度分别为1.20/0.32/0.28/0.30/0.35/0.90 mm,直径为25 mm;缓冲层材料采用TPX,直径为28 mm;二级飞片材料选用高阻抗材料Ta,直径为10 mm,厚度为0.5 mm;发射管材料采用93W,发射管长度为12.0 mm,一级飞片发射速度设定为6.8 km/s。发射腔计算设计的主要目的是通过调整TPX段的发射腔结构来调整径向上汇聚的能量,以提高二级飞片的速度。
由于二级飞片自由面上各点速度不一致,因此不同位置(或不同时刻)的平面性有所差异,本研究仅关注击靶位置处二级飞片自由面的平面性。击靶位置选取为发射管出口外2 mm处。定义两个参数δ、Φ来描述击靶位置处飞片自由面的平面性,如图2所示,δ为飞片自由面最高点和最低点的距离(不考虑飞片两端突出的尖端部分),Φ表示自由面的平面性范围。二级飞片平面性的优劣主要由δ表征:δ越小,平面性越好,反之则平面性越差。此外,以R表示二级飞片自由面上的点到二级飞片自由面中心位置的距离,则自由面上的速度差异定义为
(2)
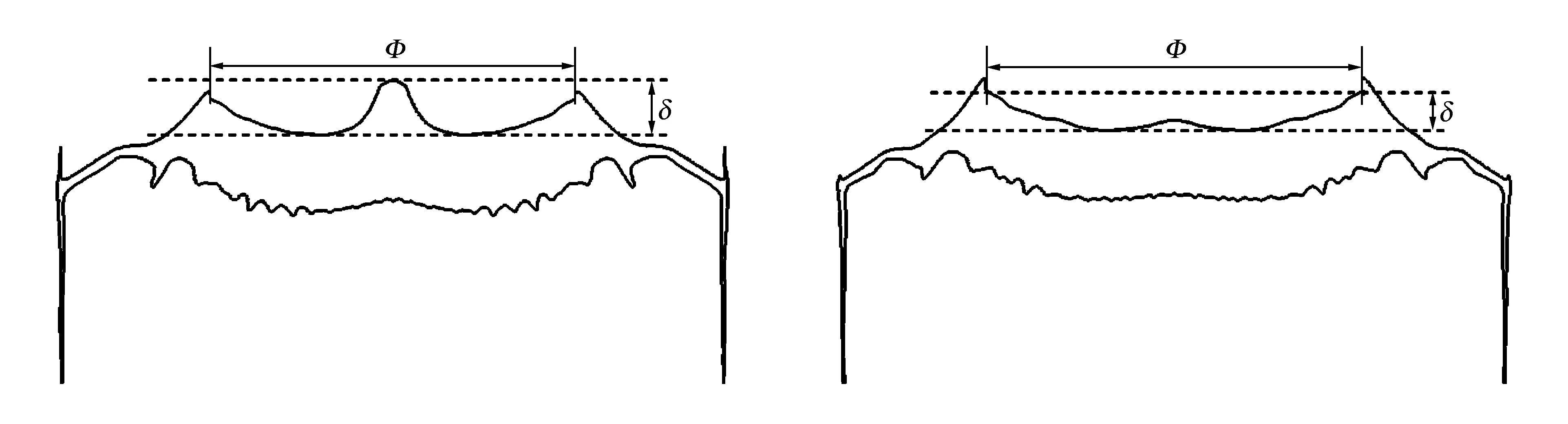
图2 平面性参数δ和平面性范围Φ的定义 Fig.2 Definition of the planarity parameters δ and Φ
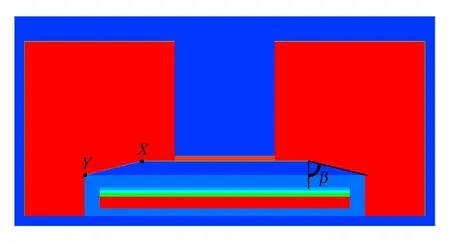
图3 发射腔角度β的示意图 Fig.3 Schematic of the cavity’s angle
为了便于描述,定义图3中的X、Y两点连线与竖直方向的夹角为发射腔角度β。若初始时刻发射腔的两个端点X和Y正好分别是二级飞片和缓冲层TPX后界面的端点(如图4第2种构型),则可由二级飞片和TPX的直径以及TPX的厚度确定一个临界的值βcr
(3)
根据β值的不同,存在图4中的4种不同的发射腔结构:(1) 0<β<βcr,(2)β=βcr,(3)βcr<β<90°,(4)β=90°,其中第4种发射腔构型即为目前汇聚型超高速发射装置的基本构型,计算设计的目的是研究前3种发射腔构型对二级飞片速度、速度差异和平面性的影响。在计算设计时,保持其他参数不变,仅对缓冲层TPX段的发射腔进行调整,相当于调整TPX的结构,故本研究选取TPX的参数进行计算,TPX厚度选为1.4、1.6和1.8 mm,对应的βcr分别为81.2°、79.9°和78.7°。
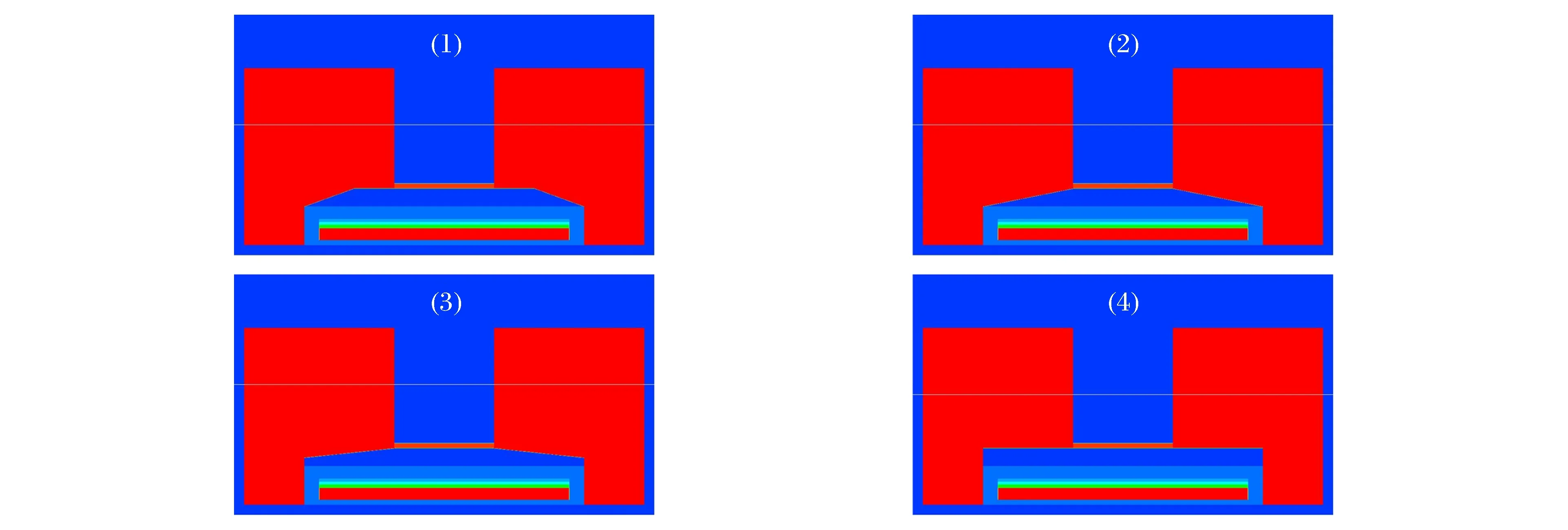
图4 4种不同类型的发射腔结构 Fig.4 Four kinds of different configurations for the cavity
图5给出了二级飞片自由面中心位置的速度随发射腔角度的变化曲线,速度随发射腔角度的增加呈先增加后减少的趋势。二级飞片的速度与发射腔角度和TPX厚度相关:当β⟩βcr(第3种和第4种发射腔构型)时,速度变化幅度较大,发射腔角度较小的变化会导致速度较大的变化,但相同发射腔角度下的速度与TPX厚度几乎没有关系;当β⟨βcr(第1种和第2种发射腔构型)时,速度增幅相对较小,在相同的发射腔角度下,TPX越厚,其速度越大,表明TPX厚度的增加提高了传递给二级飞片动能和动量的效率。一旦TPX厚度增加到一定程度使当前的发射腔角度变为βcr,继续增加TPX厚度对二级飞片速度影响较小。
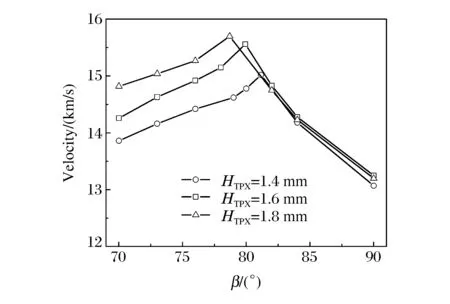
图5 二级飞片自由面中心位置速度随发射腔角度β的变化 Fig.5 Velocity variation at the center of the free surface of the flier plate with the angle’s changes
二级飞片的速度在β=βcr时取最大值,在TPX厚度为1.8 mm时中心位置最大速度可达15.85 km/s,相应的速度增益可达2.33,与第4种发射腔构型相比,速度提高了20.2%,如表1所示。需要说明的是,自由面上除中心位置外其他各处速度也得到大幅度提高,但幅度相对较小。实际上,β=0°的第1种发射腔结构即为β=90°的第4种发射腔结构,而在β⟨βcr时速度随发射腔角度的减少而降低,可以推测在β⟨βcr范围内,二级飞片速度在β=0°时取极小值,该极小值即β=90°的二级飞片的速度值,故前3种发射腔的二级飞片速度均不会低于第4种发射腔的二级飞片速度。因此,前3种发射腔构型能大幅度提高二级飞片的速度,提高传递给二级飞片动量和动能的效率,特别是第2种发射腔构型能最大幅度提高汇聚效果,提升二级飞片速度,且适当地增加TPX厚度也可以延长汇聚作用时间,进一步提升二级飞片速度。
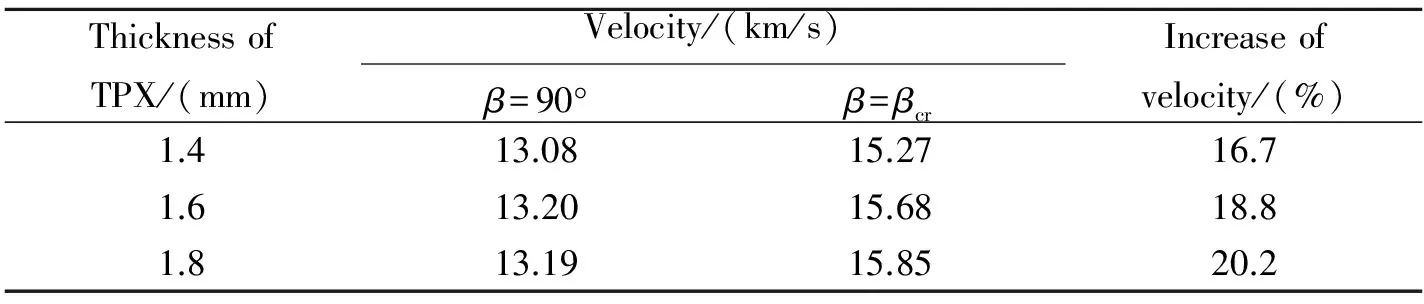
表1 3种TPX厚度下发射腔角度为βcr和90°的速度比较 Table 1 Velocity comparisons of βcr and 90° under three different thicknesses of TPX
超高压状态下材料状态方程的测量不仅要求二级飞片有较高的速度,而且要求其自由面的平面性参数δ和自由面各点速度差异尽可能小,而平面性范围Φ尽可能大。图6(a)给出了击靶位置处二级飞片自由面的平面性参数δ随发射腔角度的变化曲线。随着发射腔角度的增加,δ呈先增加后减少再增加的变化趋势,δ在β=βcr处取最小值,表明在该发射腔角度下,击靶位置处的二级飞片击靶平面性最好。与速度变化不同的是,δ的最大值并非在β=90°时取得,当β⟨76°时,其相应的平面性参数δ的值大于β=90°时的δ值,这与二级飞片中心部分受较强的汇聚作用而呈现前凸的形态密切相关。
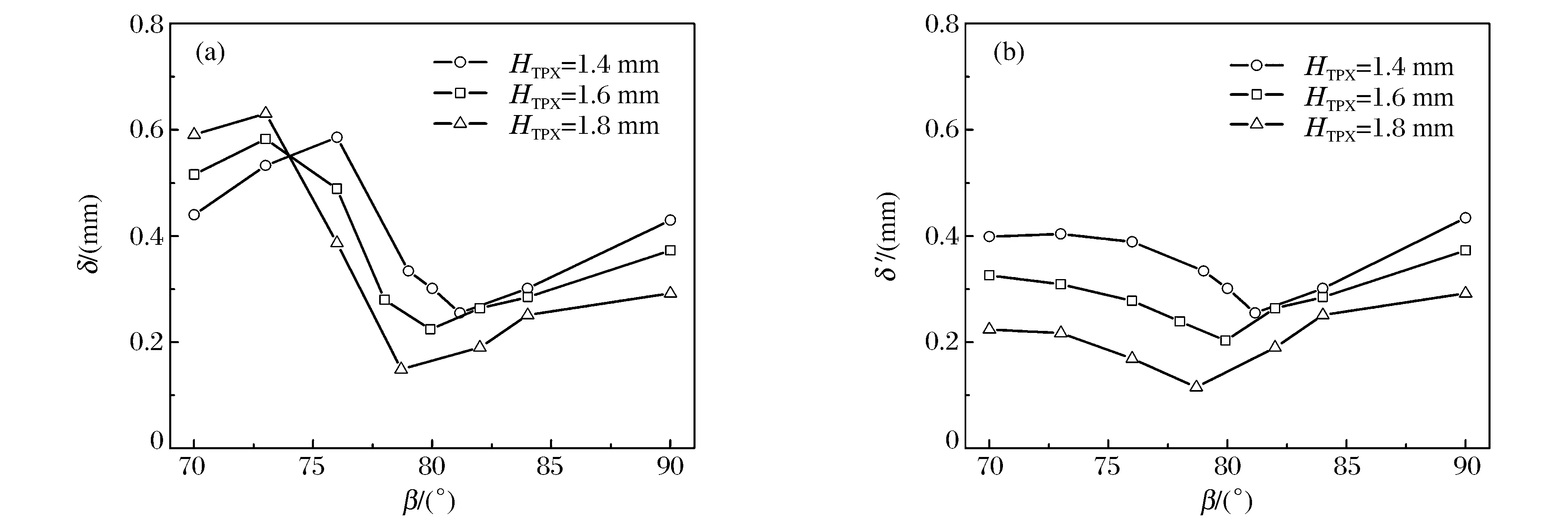
图6 (a) 击靶位置处二级飞片的平面性参数δ分布;(b) 不考虑二级飞片中间凸出部分时平面性参数δ′分布 Fig.6 (a) Distribution of planarity parameter δ of the flier plate at the impact location;(b) Distribution of planarity parameter δ′ of the flier plate when the convex portion of the flier plate is not considered
图7给出了TPX厚度为1.4 mm、发射腔角度分别为70°、76°、βcr和90°时的二级飞片变形过程。当β为70°和76°时,二级飞片中间突出部分极为明显,表明该部分受到的汇聚效应相对较强,极大地影响了平面性参数δ的值。在β<βcr时,随着发射腔角度的增加,二级飞片中间部分的突出程度呈先增强后减弱的趋势,导致了此范围内的平面性参数δ也呈现类似的变化趋势。若以δ′表示不考虑二级飞片中间突出部分的平面性,其变化趋势如图6(b)所示,可以看出,δ′随发射腔角度的减小呈现先减小后增加的趋势,在β=βcr处取最小值,在β=90°时取最大值,这与前文的结果类似。当β减小到一定程度时,δ′变化较小,表明继续减小发射腔角度β带来的平面性改善效果不显著。
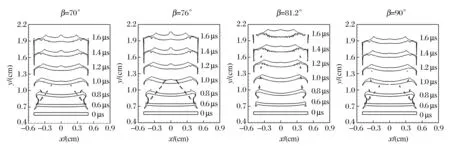
图7 TPX厚度为1.4 mm时β=70°、76°、βcr和90°时的二级飞片变形过程 Fig.7 Deformations of the flier plate at the angle of 70°,76°,βcr and 90°(The thickness of TPX is 1.4 mm)
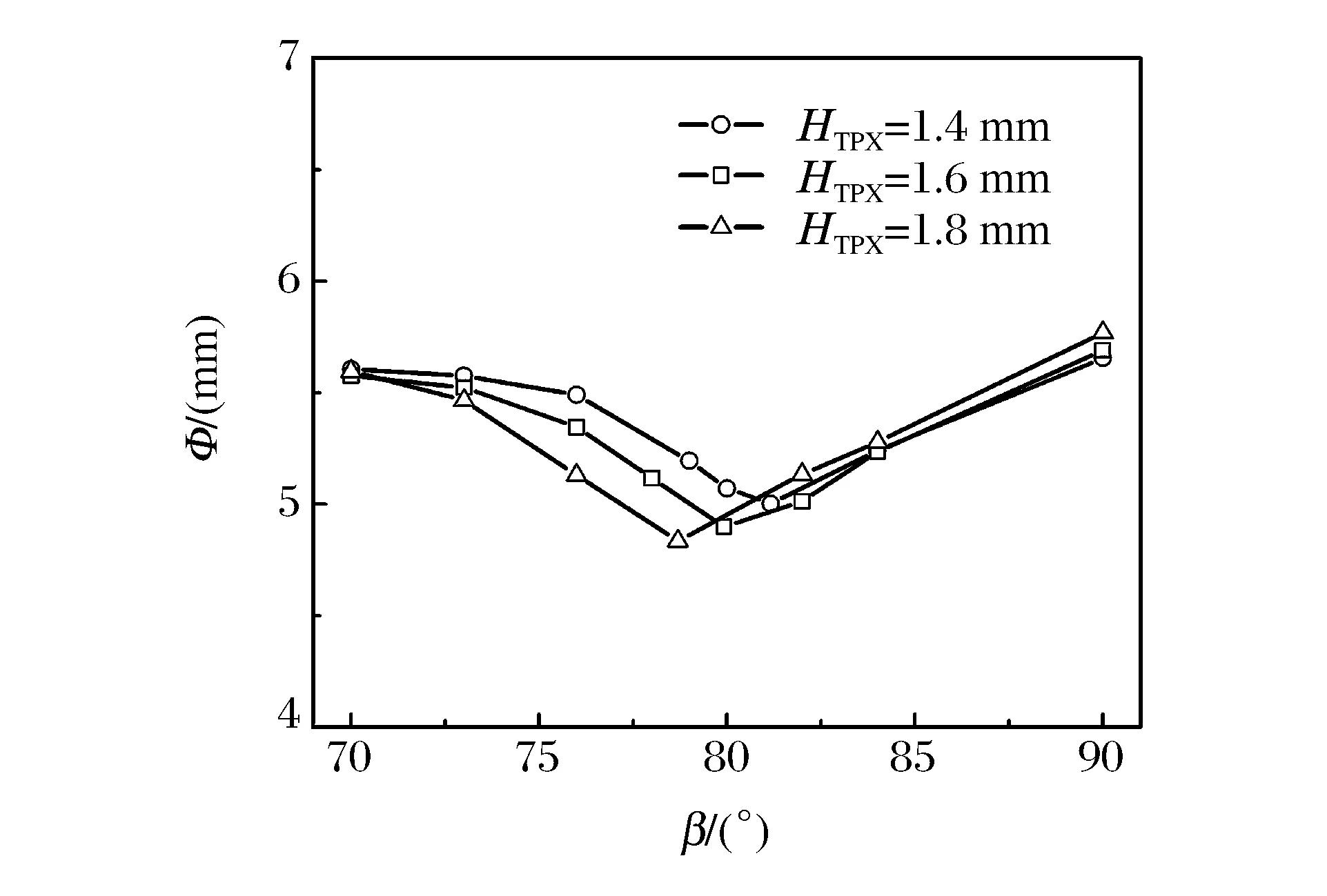
图8 不同TPX厚度下平面性范围随发射腔角度的变化 Fig.8 Effect of the angle on the range of the planarity with different TPX thicknesses
不同发射腔角度下的二级飞片平面性参数Φ(见图8)的变化趋势与δ′的变化趋势类似,与速度变化趋势相反:随着β的增加,Φ呈先减小后增加的趋势,在βcr处取最小值,而在β=90°时取最大值。在相同的β下,TPX越厚,平面性范围越小。平面性范围的变化与汇聚效应的强弱密切相关,前文已经提到:第1种和第2种发射腔结构的汇聚效应较强,而后两种发射腔结构的汇聚效应相对较弱。由于二维效应的存在,二级飞片不仅存在轴向的速度,也存在一定的径向速度,使二级飞片两侧往中间部分运动,图7的二级飞片变形过程也描述了这一现象。汇聚效应越强,此运动越显著,二级飞片自由面的平面性范围越小,且二级飞片厚度也会相应增加。故二级飞片自由面的平面性范围的变化趋势与速度变化趋势相反。
虽然二级飞片自由面各点的最终速度可能会达到稳定态,但各点的稳定速度存在差异,图9给出了二级飞片自由面上R=1 mm和2 mm处的速度差异。速度差异随着发射腔角度的增加大致呈现减小的趋势,表明前3种发射腔构型虽然能够大幅度提高汇聚效应,提升二级飞片的最终速度,但同时缩小了平面性范围,增大了二级飞片自由面速度差异,二级飞片的平面性参数δ随时间(或位置)的变化而变化,飞片的平面性难以维持。
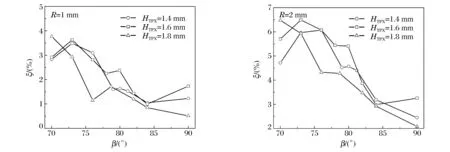
图9 R=1 mm和2 mm处的速度差异随发射腔角度的变化 Fig.9 Effect of the angle on velocity differences at R=1 mm and 2 mm
4 结 论
使用多介质流体高精度计算程序(MFPPM)对汇聚型超高速发射装置中的发射腔进行了优化设计,提出了3种改进的发射腔结构,大幅度提高了二级飞片自由面的速度,但降低了其平面性范围,增加了自由面各点的速度差异。在当前3种TPX厚度下,当发射腔角度为βcr时,二级飞片自由面速度最高,二级飞片在击靶位置的平面性最好,但平面性范围最小。在一定范围内,TPX厚度的增加也会提高二级飞片的速度。将发射腔角度减小后,二级飞片自由面速度差异较大,在不同的位置飞片的平面性参数δ会有明显不同,二级飞片相对平坦的姿态难以维持,故改进的发射腔构型不能直接运用到材料超高压状态方程的测量,但可以运用于空间碎片防护等相关领域的研究。
[1] ASAY J R,CHHABILDAS L C,FURNISH M D.The use of high velocity launchers for scientific and engineering studies [C]//TAKAYAMA K.Shock Waves:Proceedings of the 18th International Symposium.Berlin:Springer-Verlag Berlin Heidelberg,1991:103-111.
[2] MARSH S P,TAN T H.Hypervelocity plate acceleration [C]//SCHMIDT S C,DICK R D,FORBES J W.Shock Compression of Condensed Matter-1991.Amsterdam:North-Holland,1992:1033-1039.
[3] CHHABILDAS L C,DUNN J E,REINHART W D,et al.An impact technique to accelerate flier plates to velocities over 12 km/s [J].Int J Impact Eng,1993,14(1/2/3/4):121-132.
[4] CHHABILDAS L C.Hypervelocity launch capabilities to over 10 km/s:SAND 91-1374C [R].Albuquerque,NM:Sandia National Laboratories,1991.
[5] CHHABILDAS L C,TRUCANO T G,REINHART W D,et al.Chunk projectile launch using the Sandia Hypervelocity Launcher Facility:SAND 94-1273 [R].Albuquerque,NM:Sandia National Laboratories,1994.
[6] CHHABILDAS L C,KMETYK L N,REINHART W D,et al.Enhanced hypervelocity launcher capabilities to 16 km/s [J].Int J Impact Eng,1995,17(1/2/3):183-194.
[7] THORNHILL T F,CHHABILDAS L C,REINHART W D,et al.Particle launch to 19 km/s for micro-meteoroid simulation using enhanced three-stage light gas gun hypervelocity launcher techniques [J].Int J Impact Eng,2006,33(1):799-811.
[8] 柏劲松,华劲松,沈 强,等.超高速发射实验模型的数值计算 [J].高压物理学报,2004,18(2):116-122.
BAI J S,HUA J S,SHEN Q,et al.Numerical simulation of the experimental hypervelocity launcher [J].Chinese Journal of High Pressure Physics,2004,18(2):116-122.
[9] 柏劲松,华劲松,唐 蜜,等.超高速发射实验及其数值分析 [J].应用力学学报,2008,25(2):177-180.
BAI J S,HUA J S,TANG M,et al.Experimental research and numerical analysis for hypervelocity launch [J].Chinese Journal of Applied Mechanics,2008,25(2):177-180.
[10] 柏劲松,谭 华,李 平,等.阻抗梯度飞片加载下的超高速发射二维数值模拟方法 [J].计算物理,2004,21(4):305-310.
BAI J S,TAN H,LI P,et al.Numerical simulation method for 2-D hypervelocity launcher under the graded density impactor drives [J].Chinese Journal of Computational Physics,2004,21(4):305-310.
[11] 柏劲松,沈 强,唐 蜜,等.超高速发射中缓冲层材料对钽飞片速度影响的数值分析 [J].高压物理学报,2008,22(1):19-24.
BAI J S,SHEN Q,TANG M,et al.A numerical analysis of the influence of buffer material on tantalum flier plate velocity in the hypervelocity launcher [J].Chinese Journal of High Pressure Physics,2008,22(1):19-24.
[12] BAI J S,LI P,TAN D W.Simulations of the instabilities experiments in stratified cylindrical shells [J].Chin Phys Lett,2006,23(7):1850-1852.

