基于自适应四参数估计的电罗经航向运动建模

夏卫星，杨晓东

(海军潜艇学院，山东 青岛 266001)

基于自适应四参数估计的电罗经航向运动建模

夏卫星，杨晓东

(海军潜艇学院，山东 青岛 266001)

为减小舰船直航时风、流、摇摆等干扰对电罗经航向的影响，提高电罗经指向精度，采用小波变换对电罗经直航向数据进行消噪处理，获得较为平稳的信号；对消噪后的信号经能量频点分析并傅里叶展开；基于改进的四参数估计法，对直航向信号建立自适应迭代预测模型，并与实测数据进行验证对比。结果表明，采用小波分析、傅里叶级数同四参数估计相结合的自适应建模方法适用于电罗经直航向建模，航向预测效果优于传统四参数估计法。

四参数估计法；小波变换；傅里叶变换；电罗经

0 引 言

舰船作直航向航行时，由于受风浪、流、舰船摇摆等干扰造成电罗经航向幅值摆动，出现电罗经航向不稳的现象，在一定程度上影响了利用电罗经航向值观测目标的精度。因此，研究电罗经航向输出值摆动变化规律，提高电罗经航向值的可靠性具有重要的实用价值。小波分析以其时频多分辨分析的优良特性特别适宜于分析和处理非平稳信号，利用小波分析具有很好的消噪效果特性[1]，通过对获得的原始数据进行小波变换可以得到滤除噪声后的有用信号。傅里叶变换（Fourier transformation）是一种时-频域转化的分析方法，能够提取时域信号的频率特征[2]。四参数估计法是一种基本的信号处理方法，在很多场合下得到应用，如评价数据采集系统的有效位数、采集速率、交流增益、通道间延迟、触发特性等。文献[3]指出，多数四参数正弦波拟合算法的共同缺点是拟合过程需要大量迭代运算时间，从而影响了算法的效率和实时性应用。

本文通过对电罗经实测数据采用小波消噪后的数据进行傅里叶分析，确定能量频点，既可避免迭代运算过程，又可通过不断获得的新信息，采用自适应四参数估计法对电罗经直航向模型进行实时地自适应高精度估计预测。文中提出的方法为估计电罗经航向提供了一种思路。

1 小波变换

小波变换作为一种时频分析工具，它具有时间域和频率域的良好局部化性质。所谓小波是指由基本小波经伸缩和平移后形成的一簇函数[4]：

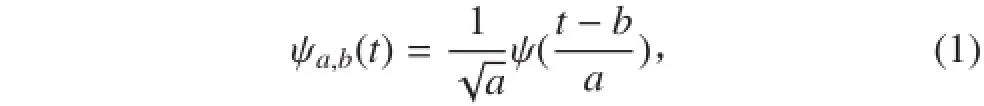
式中：a 为尺度参数，它改变滤波器的频带宽度；b 为位置信息，它决定小波变换的空域和时域信息。

则待分析信号 s（t）的小波变换为[4]：

式中：s（t）为时间信号；t 为时间。

通过适当选择参数 a、b 值，使得小波变换在时频平面上形成一种合适的网格，即可以形成多分辨率的窗口。

小波用于消噪和函数逼近是 Donobo 等的研究[3]，本文采用 db5 小波对电罗经直航向数据进行 5 层分解。选取稳定航向 H=222° 的 1 组实测数据进行分析，结果如图1 所示。

经过小波重构后的电罗经信号和原始信号相比变得更加平滑，有效抑制了高频扰动，如图2 所示。

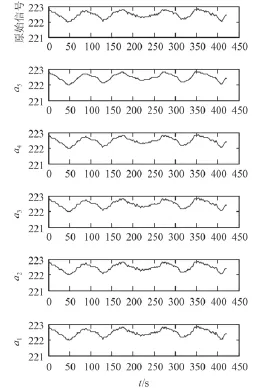
图1 小波分析Fig. 1 Wavelet transform

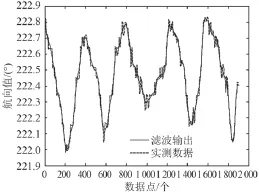
图2 小波滤波信号Fig. 2 Signal of wavelet filter

2 傅里叶变换

对于信号的分析既可以在时域中进行，也可以在频域中进行。傅里叶变换是将信号从时域变换到频域，在信号分析中占有极其重要的地位。

一维离散傅里叶变换的定义：如果有一个向量x（n），其离散傅里叶变换结果为 x（k），x（k）与x（n）的关系如下[5-6]：

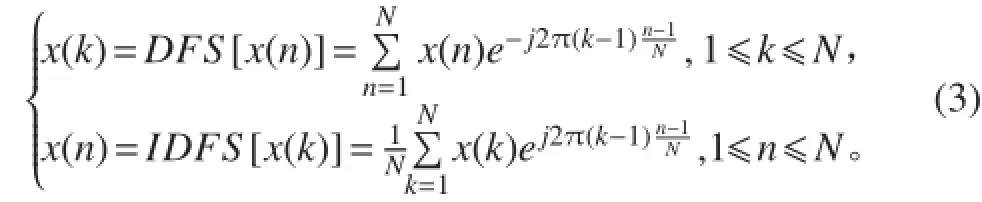
式中：N 为向量 x（n）的长度；DFS 为离散傅里叶级数的正变换；IDFS 为离散傅里叶级数的逆变换。

本文通过傅里叶变换提取直航向信号的频谱特性。取样频率 fs与取样周期 T 的关系为 fs=1/T[7]，设序列的周期为 NT，则对频谱取样的谱间距为 1/NT。

首先，提取第 1 个周期 T1的频谱特性，频谱间隔为 1/T1；其次，提取第 2 个周期 T2的频谱特性，频谱间隔为 1/T2。

由图3 和图4 可知，通过傅里叶变换可以方便快捷地提取原始信号的频谱特性，通过图可以有效提取信号的基波和谐波分量。

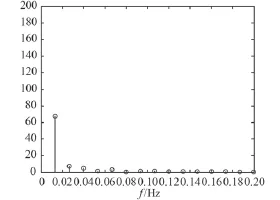
图3 T1频率特征Fig. 3 frequency characteristics of T1

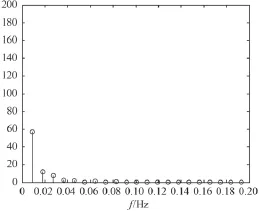
图4 T2频率特征Fig. 4 frequency characteristics of T2

3 傅里叶级数法建模

3.1 四参数的定义

设被采样的正弦信号为：

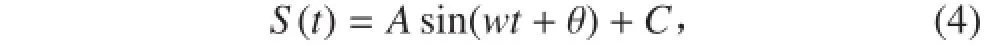
式中：A 为信号幅度；w 为信号频率；θ 为信号相位；C 为信号的常值偏移。

对于任意正弦信号的表示均可通过采用 A，w，θ，C 四个参数加以实现，这 4 个参数称为正弦信号的四参数[8-10]。也可以用另外 4 个参数来表示：

式中余弦幅度 A0，B0，C0，w0也称为正弦信号四参数，与式（4）中的幅度、频率、相位、常值偏移在描述正弦信号特征时等价。

3.2 估计正弦信号三参数的算法

设式（5）正弦信号在 tk时刻（k=0，1，2…）的采样值为 y（k），正弦幅度、余弦幅度和常值偏移 3个参数估计值分别为 A，B，C，则估计值与真实值之间的误差平方和为：

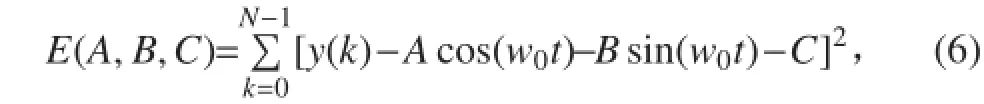
式中 N 为采样长度。

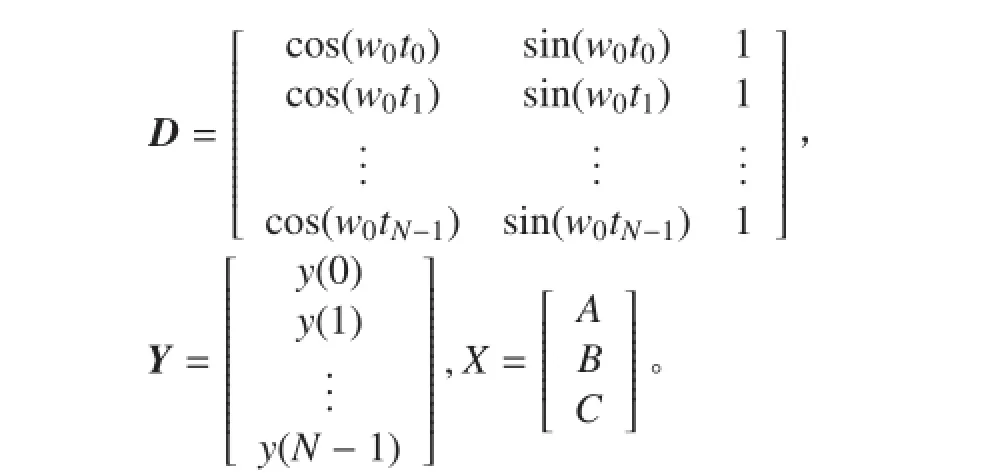
令则式（6）所描述的正弦信号中三参数的最小二乘解为[10]：

由上可知，三参数估计法就是在获得信号频率并且使式（6）中所述参差的误差平方和最小的最小二乘估计方法。四参数估计法在未知信号频率的情况下，需要进行大量的迭代计算，且计算结果并不一定收敛，因此考虑采用傅里叶变换获得高精度的频率值，这就避免了繁琐的迭代过程，并将其应用与四参数估计过程，利用上述的最小二乘估计方法求得精确的模型参数。

3.3 傅里叶展开法建模

由图2 可知，电罗经直航向信号由于受到一系列外扰及舰船本身摇摆的影响，呈现出较强的周期性摆动。由于无法用简单的周期模型进行描述，考虑采用傅里叶级数展开法进行航向建模。令直航向模型为 H=f（t），其中 H 为航向，t 为时间。通过傅里叶变换可成功提取基波和各次谐波。

由狄利克雷收敛定理可知，上述提出的模型应满足一定的条件，即设 f（t）是周期为 T 的周期函数，如果它满足：1）在一个周期内连续或只有有限个第 1类间断点，2）在 1 个周期内至多只有有限个极值点，则 f（t）的傅里叶级数收敛，并且当 t 为 f（t）连续点时，级数收敛 f（t）。

由于实测数据周期性较强，且在 1 个周期内连续，现将 H=f（t）傅里叶级数展开为：

1.3 评价标准 正常月经期子宫内膜呈线状，厚度为0.1～0.4 cm左右；增生期为0.4～0.8 cm左右；分泌晚期呈连续均匀增厚，厚度约为0.6～1.2 cm，部分患者内膜厚度可>1.2 cm，一般<1.6 cm。

式中：n 为整数，也是频点数；Ai，wi，θi，Ci为待估参数。

可将式（8）写为如下形式：

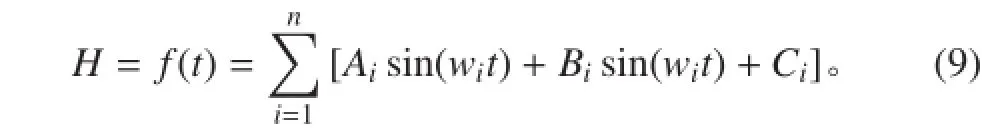
式中各参数定义同式（5）。

采用四参数法的具体估计步骤如下：

1）令 i=1，确定估计信号频率的大致区间，首先考虑第 1 个周期 T1，由傅里叶变换可以得到基波和谐波分量。由图3 可知，能量越大对信号的影响越大，因此选取基波在内的前 5 个频点。

2）令基波信号频率为 w01，其余四点谐波频率分别为 w02，w03，w04，w05，5 个频点间隔为为叙述简便，仅以基波为例进行讨论，令迭代频率区间下限wi=w01– wc/N，迭代区间频率上限 wh=w01+ wc/N（其中，wc为时钟频率，N 为 FFT 长度）。

4）比较步骤3）中的 2m+ 1 个误差平方和，选取误差平方和最小的 Aij，Bij，C1j，w1j，而为四参数的第1 次估计值，其中频率最大估计偏差

6）令新区间为 [wi，wh]，等间距的取 2m+ 1 个点，重复步骤 3 和步骤 4，计算出对应的参数估计值和误差平方和。令其为第 i 次估计值。

7）重复步骤 3 和步骤 4，直到找到满足精度要求的信号频率，同时估计出其他 3 个参数，则最终的A，B，C 和 w 为四参数的高精度估计值。其中，频率估计的最大误差为

8）以上步骤为第 1 周期的参数估计，在获得了高精度的模型后，可以有效地对第 2 个周期航向数据进行实时地预测，同时当获得第 2 周期实测数据后，又可以对模型参数进行更新修正，即不断利用新信息计算新时刻的模型，从而满足对第 2 周期中下一时刻的高精度预测要求。

由以上所述步骤可知，在每个周期中重复步骤 1 ～步骤 7 就可以获得高精度的自适应电罗经航向模型，同时可以人为的增大迭代次数 i 来提高精度。

4 模型验证

本文采用第 1 节所选择的实测数据进行验证，首先通过小波变换进行高频消噪处理，获得较为平稳的航向信号，采用傅里叶变换将航向的时域信号转化为频域信号进行分析，确定能量较高的前 5 个频点，对第 1 个周期进行建模，同时对第 2 个周期进行自适应预测，即在不断获得第 2 周期实测数据的基础上不断对下一时间点作有效预测，图5 和图6 为未加自适应修正的模型输出及预测结果，图7 和图8 为加入自适应修正的四参数估计法迭代模型输出及预测结果。

由图5 ～ 图8 所示，基于正弦信号四参数估计法的自适应估计算法能够满足预测精度要求，且具有实时性，利用不断获得的新信息采取在线修正模型参数的方法，使其能够比较真实的描述和预测电罗经直航向输出，在预测效果上明显优于传统的四参数估计法。

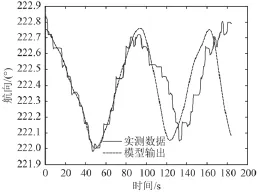
图5 估计模型与预测Fig. 5 estimationmodel and prediction

图6 预测误差Fig. 6 prediction error

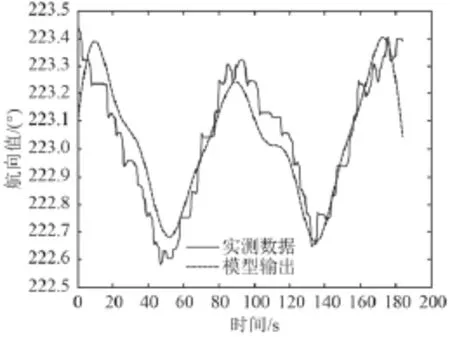
图7 自适应估计模型与预测Fig. 7 Self-adaptive estimationmodel and prediction

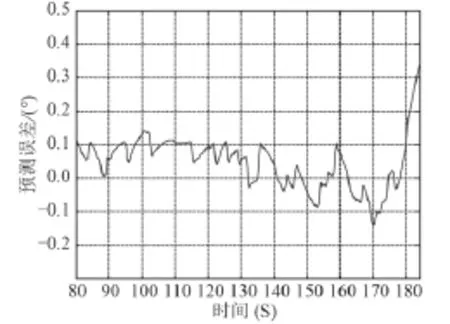
图8 自适应预测误差Fig. 8 Self-adaptive prediction error

5 结 语

潜艇机电作动系统的关键设备电机选择对于整个系统开发至关重要。预制电机设计可以最高级控制、最高可靠性、最低噪声，最有效的空间利用，但是研制费用也相对较高。使用重新封装的工业交流感应电机，是成本最低的方案。虽然机电作动系统不受太多环境限制，但在系统设计中要充分考虑电磁兼容，否则将导致电磁兼容测试的失败。为使机电作动系统发挥最大效能，采用动态系统仿真，以协助设计确定设备标准，并通过仿真认识到机电作动系统的全部能力。

[1]郭宏, 邢伟. 机电作动系统发展[J]. 航空学报, 2007, 28(3): 620-627. GUO Hong, XING Wei. Development of electromechanical actuators[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 620-627.

[2]沙南生, 李军. 功率电传机载一体化电作动系统的研究[J]. 北京航空航天大学学报, 2004, 30(9): 909-912. SHA Nan-sheng, LI Jun. Research on airborne power-by-wire integrated electrical actuation and control systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(9): 909-912.

[3]宋辉, 王旺球, 陈华锋. 一种直流配电系统电磁兼容性分析及试验[J]. 舰船科学技术, 2016, 38(4): 116-119. SONG Hui, WANG Wang-qiu, CHEN Hua-feng. Analysis and test of EMC foraDC power distribution system[J]. Ship Science and Technology, 2016, 38(4): 116-119.

[4]马伟明. 电力电子在舰船电力系统中的典型应用[J]. 电工技术学报, 2011, 26(5): 1-7.mA Wei-ming. Typical applications of power electronics in naval ship power systems[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 1-7.

[5]Richard Cooke, Dorset Green Technology Park, Integrating external electric drive actuation systems into the submarine, UDT2010.

[6]LC Goodenough R H, Osborne N P. Electrical actuation of submarine hydrodynamic control surfaces (2)[J]. J Nav Eng, 2009, 45(2).

[7]付永领, 刘和松, 庞尧, 等. 用于直驱式机电作动器的PMSM自抗扰控制研究[J]. 四川大学学报(工程科学版), 2011, 43(2): 121-127. FU Yong-ling, LIU He-song, PANG Yao, et al. Active disturbance rejection control for the PMSmUsed in the direct drive EMA[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(2): 121-127.

[8]张阳阳, 尹成斌, 邢继峰. 机电作动器系统设计及动态特性研究[J]. 液压气动与密封, 2014, 34(6): 26-28. ZHANG Yang-yang, YIN Cheng-bin, XING Ji-feng. Design and dynamic characteristics study of electromechanical actuator system[J]. Hydraulics Pneumatics & Seals, 2014, 34(6): 26-28.

Modeling the course data of electromagnetic controlled gyrocompass based on self-adaptive four parameters

XIA Wei-xing, YANG Xiao-dong
(Naval Submarine Academy, Qingdao 266001, China)

In order to reduce the linear course error and enhance the heading accuracy of Electromagnetic Controlled Gyrocompass, based on wavelet to denoising, obtain amuchmore smooth signal, based the signal,make use of Fourier transformto do the time/frequency switch, analysis the signal with frequence spots' energy,modeling with the Fourier Expansionmodel based on the improved 4 parameters estimation of sine-wave,modelingaself-adaptivemodel to predict the course of electromagnetic controlled gyrocompass inahigh accuracy. The prediction and the data indicates that combine the self-adaptive 4 parameters estimation with wavelet and fourier expansionmodel of the course data could haveagood description, it is better than formal 4 parameters estimation.

four parameters estimation；wavelet transform；Fourier transform；electromagnetic controlled gyrocompass

U666.1

：A

1672 - 7619(2016)10 - 0125 - 04

10.3404/j.issn.1672-7619.2016.010.025

2015 - 12 - 14；

2016 - 01 - 06

夏卫星(1985 - )，男，博士，讲师，研究方向为航海导航。