音乐中的数学

刘 哲



音乐中的数学

刘 哲

摘 要：通过操作，让我们领略到了音乐的奇妙，以及看到了音乐（如弦乐器）从它进入人类的生活、娱乐的初始，就有数学与之相随了，对它的初探，只是起到一个抛砖引玉的作用，如果我们再进一步研究，将会有更新的发现和认识。

关键词：音乐；数学

提到音乐与数学，人们一定会感觉到他们风马牛不相及，怎么会联系到一起呢？通过向下面的观察，我们就会发现，他们之间有着一种奇妙的关系。

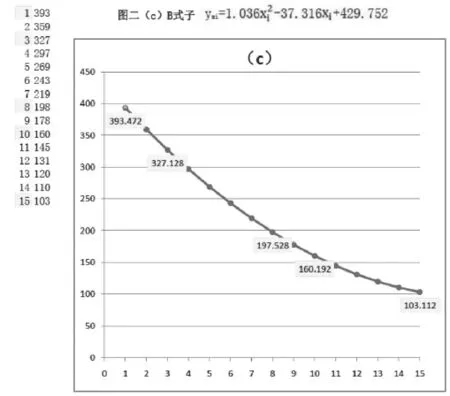
二胡弦长数据参考对照表

纵坐标y x i（弦长）推导式及计算数据横坐标序号及对应唱名粗测弦长数据y x i （m m ）= L （x i -1 ）= 1 . 0 3 6 A -3 7 . 3 1 6 + 4 2 9 . 7 5 2 B X i　唱名1 　 1 （d o）　4 0 0 　4 0 0 　3 9 3 . 4 7 2 2 　 2 （r e）　3 6 0 　3 6 2 . 2 8 9 　3 5 9 . 2 6 4 3 　 3 （m i）　3 2 4 　3 2 8 . 1 3 4 　3 2 7 . 1 2 8 4 　 4 （f a）　2 9 6 　2 9 7 . 1 9 8 　2 9 7 . 0 6 4 5 　 5 （s o l）　2 6 6 　2 6 9 . 1 8 0 　2 6 9 . 0 7 2 6 　 6 （l a）　2 4 0 　2 4 3 . 8 0 2 　2 4 3 . 1 5 2

7　 7（si）　216　220.817　219.304 8　（do）　200　200　197.528 9　（re）　180　181.144　177.824 10　（mi）　162　164.067　160.192 11　（fa）　148　148.599　144.632 12　（sol）　133　134.590　131.144 13　（la）　120　121.901　119.728 14　（si）　108　110.409　110.354 15　（do）　100　100　103.112

以下我们再介绍一下方程式的出处。这里重点介绍一下B式导出的依据。上世纪七、八十年代，我在山西省电子工业厅计划处工作时，曾代表电子系统参加过全省规划的编制，当时也曾是省计划学会的会员，在工作中摸索出一种计算回归的简化方法，在实践中得到了很好的应用。之所以称为简化，是它不需要高深的数学，也不必用最小二乘法计算，运用简便。该方法曾撰文在一九八八年《山西统计》第五期杂志上发表，该法建立在一个有规律变化的一组数据基础上推导出来的，见该刊第五页图一，设各组数据按y=f（x）的方程变化，按照这一规律，各组数据的方程式表达式为：

在该方程中，x1，x2，x3，…xm（横坐标）及y1，y2，y3，…ym（纵坐标），作为已知数出现，而a，b，c，…等作为未知数参与运算，这样方程式就可以建立起来了。其方程式可表达如下：

将（1.2）式中的m个方程等号两边各自相加，组合成数量大体相等或接近的3个方程式组。因为是非线性方程，所以三个未知数必须是三个方程，即按三个未知数列出以下的联立方程，并求解。

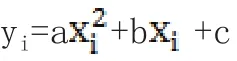
最终运算结果为：

a=1.036

b=-37.316

c=429.752

将a，b，c代入方程则最终得到的方程式为：

该方程由于测量方法简单，误差不小，所以在音准方面不一定准确，但大致可以看出它们的相互关系。

通过以上的操作，让我们领略到了音乐的奇妙，以及看到了音乐（如弦乐器）从它进入人类的生活、娱乐的初始，就有数学与之相随了，对它的初探，只是起到一个抛砖引玉的作用，如果我们再进一步研究，将会有更新的发现和认识。■