纵-扭复合超声振动加工系统设计及频率简并研究
袁松梅, 刘 明(1.北京航空航天大学 机械工程及自动化学院,北京 100191;2.北京市高效绿色数控加工工艺及装备工程技术研究中心,北京 100191)
纵-扭复合超声振动加工系统设计及频率简并研究
袁松梅1,2, 刘明1,2(1.北京航空航天大学 机械工程及自动化学院,北京100191;2.北京市高效绿色数控加工工艺及装备工程技术研究中心,北京100191)
摘要:纵-扭复合超声振动加工技术在硬脆性材料的加工中受到越来越多的重视,针对该种需求,设计了一种纵-扭复合超声振动加工系统,基于有限元方法对该类系统普遍存在的频率简并问题进行了研究。利用数值解析方法设计出超声换能器和超声变幅杆,之后在变幅杆上做出螺旋槽,一部分纵向振动转换为扭转振动;以目标频率附近的纵、扭谐振频率尽量接近为原则,利用有限元软件分析系统的结构参数对纵、扭谐振频率的影响规律,实现频率简并;在此基础上对系统进行模态分析和瞬态动力学分析,结果表明系统可以实现纵-扭复合超声振动,验证了此种频率简并方法的有效性和实用性。
关键词:纵-扭复合超声振动;螺旋槽;频率简并;有限元分析
随着科技的发展,超声振动加工(Ultrasonic Machining, USM)在硬脆材料加工中得到越来越多的应用[1],作为一种超声加工形式,纵-扭复合超声振动技术在许多领域也得到了日益广泛的应用。
纵-扭复合超声振动首先应用于超声电机中[2],杨淋等[3]设计了一种大力矩纵-扭复合超声电机,采用了纵振压电陶瓷片全部粘贴到定子端面的结构,所研制的超声电机堵转力矩达到1.28 N·m。在超声焊接中[4],纵-扭复合超声振动焊接相比于其他线性振动焊接有着更优良的性能,利用较小的振幅就能将工件焊接在一起,而形变量却要小很多。在超声加工方面,皮钧等[5]指出纵-扭共振旋转超声切削不受加工材料的限制,比单一轴向振动旋转超声加工具有更好的加工特性;在某些材料的钻孔中,与传统加工方法相比,纵-扭复合超声加工在材料去除率、加工精度和加工时间方面表面优异[6];哈尔滨工业大学研制的手持式纵-扭复合振动装置[7],其振动系统主要是纵向的超声振动和低频的扭转振动复合在一起,从而达到优势互补的效果,有效地提高了振动手钻性能。
与普通超声振动加工相比,纵-扭复合超声振动不易产生,这也是该技术应用的难点之一。目前,实现纵-扭复合振动主要有两种途径:一是利用纵-扭换能器[8],对于夹心式换能器来说,方法是先将用于产生扭振的压电陶瓷片切分成若干扇形片,之后分别将各陶瓷片切向极化,再将其粘结起来,最后再与纵振压电陶瓷片结合在一起,该方法废品率高,容易出现陶瓷片极化不完全、电击穿等问题,很难制造出理想的换能器。对于磁致伸缩换能器来说,文献[9]中的超磁致伸缩复合振动超声换能器虽然也实现了复合超声振动,但是该种装置结构不紧凑,能量转换效率较低。
第二种途径是利用特殊结构的变幅杆,如文献[10],该种方法在变幅杆末端开斜槽,由于斜槽存在,部分超声能量在斜槽处发生反射,转换为扭转振动能量,另一部分超声能量则通过无斜槽区域传递到变幅杆末端,从而在末端实现纵-扭复合振动,开斜槽的方法虽然实现了纵-扭复合超声振动,但存在扭振分量小的缺点,未能充分利用纵-扭复合超声振动技术的优势;另一种特殊结构的变幅杆是复合振动变幅杆[11],如指数型变幅杆,通过数学计算可使该种变幅杆的某一阶纵振谐振频率和扭振谐振频率一致,若外界激振频率为该频率,则可实现复合超声振动,但能实现该功能的变幅杆种类较少,且需与纵-扭换能器一同使用。
纵-扭复合超声振动加工技术的另一个难点是使设计频率附近的纵振谐振频率和扭振谐振频率趋于一致,即频率简并。由于同一材料中不同振动模式的传播速度不同,因此,为了有效地激发纵-扭复合超声振动系统中不同的振动模式,必须采用不同的超声振源分别激发。为了解决这一问题,必须使复合模式振动系统中的纵振谐振频率和扭振谐振频率相同,否则,系统会出现发热多、效率低等现象。目前,针对超声加工领域的纵-扭复合超声振动频率简并问题很少有研究。
针对纵-扭复合超声振动技术应用存在的问题,设计了一套纵-扭复合超声振动加工系统,该系统扭转分量大、效率高;同时,对纵-扭复合超声振动系统频率简并问题进行了研究,有限元分析结果验证了此种频率简并方法的有效性。
1超声振动系统设计
1.1超声换能器设计
由于夹心式压电换能器比磁致伸缩换能器具有更高的能量转换效率,因此这里选择该种换能器。在换能器材料选择方面,前、后盖板的材料通常是钢、硬铝和钛合金等,后盖板选择声阻抗率较大的45号钢,前盖板用声阻抗率较小、容易加工的铝合金,压电陶瓷选择机械品质因数和压电常数较高的PZT-8型压电陶瓷,换能器的长度为半波长。由相关知识可知,若以足标n表示换能器的各个部分,则均匀等截面积的换能器振速方程为:
(1)
式中k为波数,k=ω/c=2πf/c,c为材料的声速。
振子各部分的坐标、边界条件和尺寸标注均列在图1中,方程(1)的通解为:
vn(xn)=Ansinknxn+Bncosknxn
(2)
各部分应力分布为:
Fn(xn)=-jZn(Ancosknxn-Bnsinknxn)
(3)

图1 换能器各部分标注Fig.1 Labels of each part of transducer
式中Zn=ρncnSn为各部分的声阻抗,ρn为各部分的密度,Sn为各部分的横截面积。
将节面设置在压电陶瓷与前盖板的接合处,先考虑节面右侧部分,此时节面右侧只有前盖板,边界条件为:
(4)
式中:vf为振子前表面振速,则由以上各式得到节面右侧的频率方程为:
k3l3=π/2
(5)
现在考虑节面左侧部分,左侧部分由后盖板和压电陶瓷片组成,计算时把压电陶瓷片看作纯粹的连续弹性介质,与节面右侧的计算类似,得频率方程为:
(6)
1.2变幅杆设计
变幅杆主要有阶梯型、指数型、圆锥形和复合型等类型,其中圆锥-圆柱型复合变幅杆综合了圆锥变幅杆和阶梯变幅杆的特点,具有放大系数大、形状因数高、容易加工等优点,这里选择该类变幅杆。
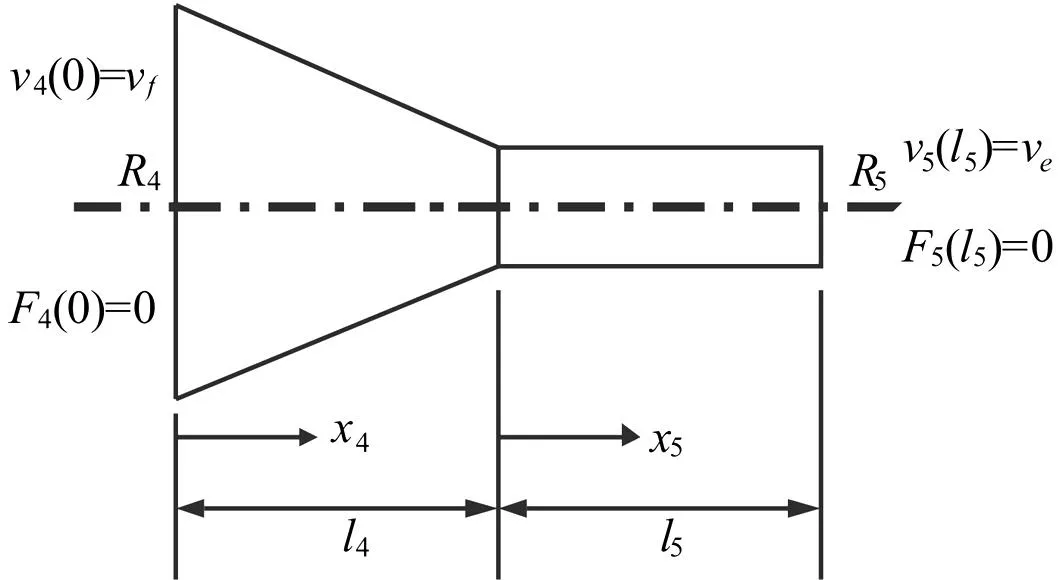
图2 圆锥-圆柱复合变幅杆Fig.2 Conical-cylindrical composite horn
如图2,对于变幅杆圆锥部分,由相关知识得其振动方程为:
(7)
其中γ=(R4-R5)/R4l4,得
v(x4)=m(Asinkx4+Bcoskx4)
(8)
(9)

对于圆锥-圆柱变幅杆,其边界条件为:
(10)
式中,vf、ve分变幅杆输入端和输出端振动速度,由式(2)、(3)、(8)~(10)得到频率方程:
(11)

设超声振动系统的共振频率f=25 kHz,每片压电陶瓷的厚度为4 mm,共4片。为了减少横向振动的影响,压电陶瓷片的直径应小于介质中超声波长的四分之一,设其为45 mm。设前盖板长度为50 mm,直径为45 mm,后盖板直径45 mm,则由式(6)计算出后盖板的长度为32 mm,内径15 mm,用于放置预紧螺栓。
对于变幅杆,设k4l4=2,圆柱段直径为15 mm,则圆锥段长度为64 mm,由式(11)得圆柱段长度为35.8 mm,纵-扭复合超声振动装置各部分尺寸如图3。
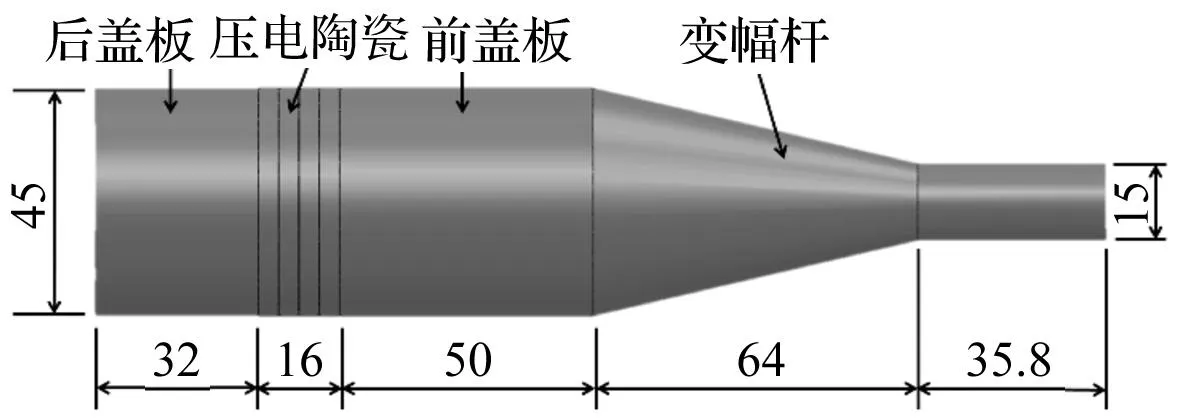
图3 纵-扭超声振动装置各部分尺寸示意图(单位:mm)Fig.3 Geometry of each part of longitudinal-torsional ultrasonic vibrationsystem
2带有螺旋槽的变幅杆设计
前面已经叙述,实现纵-扭共振的方法之一是在变幅杆末端开斜槽,虽然该种方法结构简单,但是扭转分量所占比重不大,文献[12]中已有叙述,在变幅杆上开螺旋槽的方式可以提高扭转振动所占比例,这里选择该方式来实现纵-扭复合超声振动。
螺旋槽所绕螺旋线作如下设置:螺旋线轴向长度为变幅杆圆锥段长度;螺旋线绕轴线的旋转角为180°;考虑到变幅杆圆锥段的强度,将螺旋线设计成锥形螺旋线,锥度为1∶6.4,即螺旋线所包络为一圆台,其底面直径(圆A)为30 mm,顶面直径(圆B)为10 mm。图4为前盖板与变幅杆接触面示意图,四个扇形的顶角为90°,通过扇形圆心角顶点的直径平分圆心角,四个扇形的顶点均布于直径30 mm的圆上。利用建模软件可得到所述螺旋槽,整个纵-扭复合超声振动系统如图5所示。

图4 螺旋槽形成示意图Fig.4 Settings of helical slots

图5 纵-扭复合超声振动装置Fig.5 Longitudinal-torsional ultrasonic vibration system
3纵-扭复合超声振动装置频率简并研究
超声加工中,变幅杆末端需要较大的振动振幅[13]。因此,超声振动装置需在目标频率附近的纵振谐振频率和扭振谐振频率下工作,而由于纵向振动和扭转振动在相同材料的等截面弹性体中的传播速度不同,使同阶的纵振与扭振谐振频率有较大的差异,这时就需要通过一定的方法使纵、扭谐振频率尽可能接近。
由于超声振动系统的谐振频率与系统的结构参数有直接关系,改变结构参数即可改变谐振频率,而开螺旋槽的变幅杆属非常规变幅杆,很难利用传统的解析方法得到其谐振频率,有限元方法可以很好地解决这一问题:依次改变影响系统谐振频率的结构参数,再对系统进行模态分析,找出目标频率25 kHz附近的纵振谐振频率(以下简称纵振频率)和扭振谐振频率(以下简称扭振频率)与某结构参数的变化规律,进而找出使两谐振频率距离最近的参数,实现频率简并。
3.1纵、扭谐振频率影响因素分析
螺旋槽自身参数对纵、扭谐振频率有影响的因素主要有螺旋槽个数、螺旋线旋转角等,下面分别讨论两者对两谐振频率的影响规律。
利用有限元分析软件ANSYS对装置进行模态分析,找出在目标频率25 kHz附近的纵振模态和扭振模态。首先将螺旋线旋转角设置为180°,改变螺旋槽的个数,研究螺旋槽数与纵、扭谐振频率的关系。
如图6所示,在螺旋线旋转角度一定的情况下,随着螺旋槽个数的增加,纵振频率和扭振频率都降低,两者差值先增大后减少,当螺旋槽数为10时,两谐振频率最为接近,约为509 Hz。出现这种现象的原因之一可能是系统的刚度随着旋转角度的增加而减小。

图6 螺旋槽数与纵、扭谐振频率关系Fig.6 Relationship between the number of helical slots and thelongitudinal, torsional resonant frequency
由图6可知,若从频率简并的角度考虑,螺旋槽数应选择10个,然而,随着螺旋槽数的增加,加工难度加大,且成型后的变幅杆应力集中问题严重。为此,我们可以从另一个角度确定螺旋槽数,由于超声加工中比较关注扭转分量的大小,因此,可从扭转分量最大的角度来确定螺旋槽数目,利用有限元分析软件进行模态分析,找出螺旋槽数与扭转分量的关系,从而确定螺旋槽数,由于ANSYS模态分析中的位移不是绝对位移,我们可以利用相对位移代替绝对位移。
在螺旋线旋转角一定的情况下,螺旋槽数与纵、扭振动分量的关系如图7所示,随着螺旋槽数的增加,扭振分量先增加后减少,当螺旋槽数为4时,扭振分量达到最大,此时纵振分量也较大,应力集中问题不严重,所以选择螺旋槽数为4。

图7 螺旋槽数与相对纵、扭振动分量关系Fig.7 Relationship between the number of helical slots and the relative components oflongitudinal, torsional vibration
在螺旋槽数确定后,从频率简并的角度出发,讨论螺旋线旋转角度和纵、扭谐振频率的关系,如图8。

图8 螺旋线旋转角度与纵、扭谐振频率关系Fig.8 Relationship between the helical angle and thelongitudinal, torsional resonance frequency
从图8可以看出,在螺旋槽数一定的情况下,随着螺旋线旋转角度的增大,纵、扭谐振频率都呈下降趋势,两者差值逐渐减小,在252°~360°范围内时,两谐振频率的差值几乎不变,约为480 Hz,考虑到加工的难易程度和应力集中问题,选择螺旋槽旋转角度为252°。
经过以上几个步骤,纵、扭谐振频率差值仍较大。我们知道,除螺旋槽自身属性外,系统其他部分的结构参数对纵、扭谐振频率也有影响,可以改变系统其它部分的结构尺寸继续进行频率简并,这里首先选择后盖板长度作为影响因素,研究其与纵、扭谐振频率的关系,有限元模态分析结果如图9所示。

图9 后盖板长度与纵、扭谐振频率关系Fig.9 Relationship between the length of back mass and thelongitudinal, torsional resonance frequency
可以看出,随着后盖板长度的增加,纵、扭谐振频率都呈下降趋势,两谐振频率差值几乎不变,约为475 Hz,说明后盖板长度对两谐振频率差值影响不显著。为了进一步使两谐振频率接近,设后盖板长度不变,选择前盖板长度作为影响因素,有限元模态分析结果如图10所示。
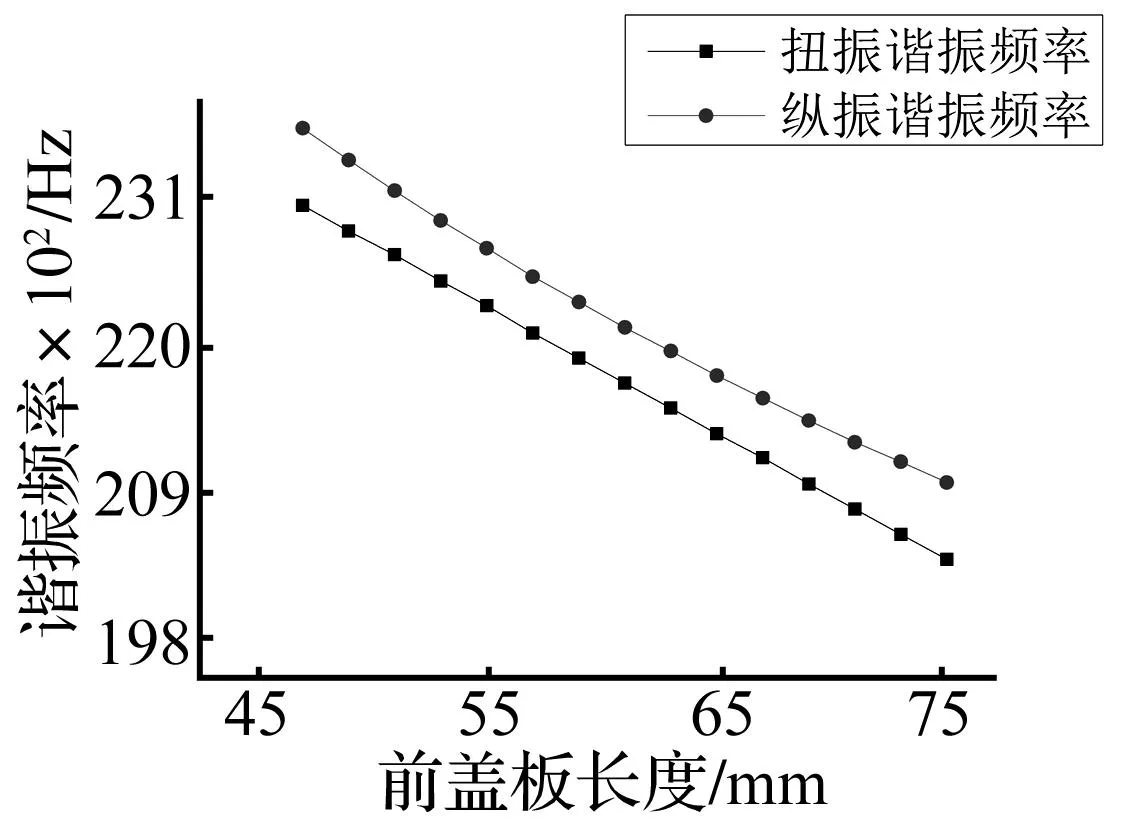
图10 前盖板长度与纵、扭谐振频率关系图Fig.10 Relationship between the length of front massand thelongitudinal, torsional resonance frequency
从图10可以看出,随着前盖板长度的增加,纵、扭谐振频率都呈下降趋势,两条曲线接近平行,两者差值呈现先减小后增加的趋势,在长度约为61 mm时差值最小,为421 Hz,为使频率差值尽量小,选择前盖板长度为61 mm。可以看出,相比于后盖板长度,前盖板对纵、扭谐振频率的影响较大。接下来选择变幅杆圆柱段长度作为影响因素进行频率简并,圆柱段长度与纵、扭谐振频率的关系如图11所示。

图11 变幅杆圆柱段长度与纵、扭谐振频率关系图Fig.11 Relationship between the length of cylindrical part of horn and the longitudinal, torsional resonance frequency
从图11可以看出,当圆柱段长度从31 mm增加到38.6 mm时,纵、扭谐振频率越来越接近;随着圆柱段长度继续增加,两条频率曲线并没有相交,而是出现了纵振模态和扭振模态的耦合;当圆柱段长度为38.6 mm时,两种模态的耦合最强烈;随着圆柱段长度继续增加,两条频率曲线逐渐分离,纵振模态和扭转模态出现解耦。经过耦合后,纵振模态和扭转模态相互交替,这与文献[14]的分析结果一致。
由于出现了模态耦合,纵振模态和扭振模态的区分已不明显。图12是在该条件下的两种模态的速度矢量图,可以看出,两种模态下,纵向振动和扭转振动已经耦合在一起,变幅杆末端圆周上的点既有沿轴向的速度分量又有沿周向的速度分量,此时系统在25 kHz附近的两种模态频率分别为21 463 Hz和21 737 Hz,两者相差274 Hz,可以认为实现了频率简并。

图12 两种模态对应的速度矢量图Fig.12 Velocity vector distributions of two modals
若使系统产生纵-扭复合超声振动,只需将外界激振频率设置在纵振模态和扭振模态耦合时的频率范围内即可,这里设置超声电源频率为两种模态频率的平均值,即21 600 Hz。经过频率简并后的的系统各部分主要尺寸如表1所示。

表1 纵-扭复合超声振动系统主要尺寸
3.2纵-扭复合超声振动系统动力学特性分析
为了得到一定简谐电压激励下变幅杆末端X,Y,Z方向位移的大小,有必要对其进行瞬态动力学分析。
瞬态动力学分析可以确定结构在静载荷、瞬态载荷和简谐载荷的随意组合作用下随时间变化的位移、应变及应力等[15]。
Full(完全法)、Reduced(缩减法)和Mode Superposition(模态叠加法)是瞬态动力学分析常用的三种方法。完全法采用完整的系统矩阵计算瞬态响应,在三种方法中功能最为强大,可以包含各种非线性特性。本文采用完全法进行瞬态动力学分析。这里需要注意,为了与实际结果尽量接近,需要设置适当的系统阻尼。
在压电陶瓷上施加幅值800 V、频率21 600 Hz和初始相角为0°的正弦电压,为了得到较为平滑的响应曲线,取15个周期,每个周期分30个时间段。通过ANSYS有限元分析软件进行瞬态分析求解,图13是变幅杆末端圆周上某点在X,Y,Z方向的位移-时间曲线,可以看出,施加电压一段时间后,振动趋于稳定,Z方向即轴向的位移较大,峰-峰值约为3.2 μm,约比X,Y方向位移大一个数量级;X,Y,Z方向的位移都呈正弦规律变化。将数据导入Origin分析软件,绘制出振动稳定后的该点的运动轨迹如图14所示。
从图14中可以看出,变幅杆末端圆周上点的轨迹为椭圆,端部圆周上的点的扭转角度最大,扭转角随半径的减小而减小,端部圆心处的扭转角为零;同时,圆心处和端部的点都沿轴向进行纵向振动,从而产生纵-扭复合超声振动。
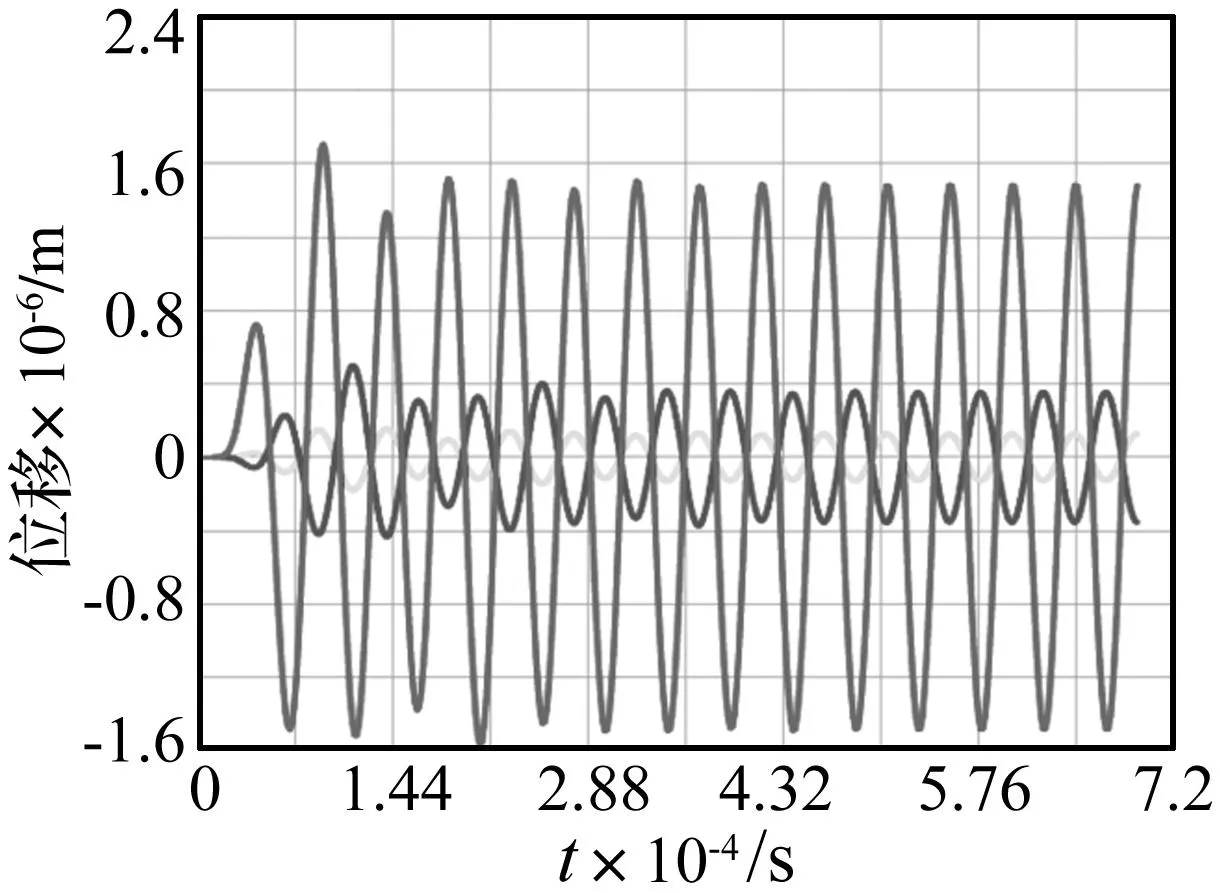
图13 变幅杆末端圆周某点X,Y,Z方向位移-时间曲线Fig.13 The displacement-time curve of X,Y,Z direction of aparticular point on the end circle of horn

图14 变幅杆末端圆周某点运动轨迹Fig.14 The motion trajectory of a certain point on the end circle of horn
4结论
相比于传统超声加工,纵-扭复合超声振动加工在钻孔、铣削等领域中表现突出,但纵-扭复合超声振动较难实现的现状限制了其应用发展。针对这一现状,在结合传统设计方法和有限元分析方法的基础上,设计了一套纵-扭复合超声振动系统,通过在变幅杆部分做出螺旋槽,一部分纵向振动转换为扭转振动,从而在变幅杆末端得到纵-扭复合超声振动。此外,基于有限元方法对纵-扭复合超声振动系统普遍存在的频率简并问题进行了研究,分析了装置的结构参数对纵-扭谐振频率的影响,从而实现频率简并。
总之,通过传统方法与有限元分析相结合的方式,根据有限元分析结果合理地选择各部分的尺寸,即可设计出扭转分量大的纵-扭复合超声振动装置,螺旋槽结构的设计思想为其他形式的纵-扭超声系统设计提供了参考,对实际生产加工具有一定的指导意义。
参 考 文 献
[ 1 ] (日)隈部淳一郎.精密加工、振动切削:基础与应用[M].韩一昆等译.北京:机械工业出版社,1985.
[ 2 ] 韩杰.纵-扭复合振动超声深滚加工声学系统研究[D].焦作:河南理工大学, 2012.
[ 3 ] 杨淋, 赵淳生. 大力矩应力型纵扭复合超声电机[J]. 振动. 测试与诊断, 2012, 32(1): 126-131.
YANG Lin, ZHAO Chun-sheng. High torque stress-type longitudinal-torsional ultrasonic motor[J]. Journal of Vibration, Measurement & Diagnosis,2012, 32(1): 126-131.
[ 4 ] Tsujino J, Uchida T, Yamano K, et al. Ultrasonic plastic welding using two 27 kHz complex vibration systems[C]//IEEE Ultrasonics Symposium, 1997, 1: 855-860.
[ 5 ] 皮钧,徐西鹏. 纵扭共振超声铣削研究[J]. 中国机械工程, 2009 (10): 1163-1169.
PI Jun, XU Xi-peng, Research on Longitudinal-tersional Resonance Ultrasonic Milling (LTRUM) [J]. China Mechanical Engineering,2009 (10): 1163-1169.
[ 6 ] Asami T, Miura H. Study of hole machining of brittle material by ultrasonic complex vibration[C]//IEEE Ultrasonics Symposium, 2012: 2667-2670.
[ 7 ] 国绍文. 手持式振动钻削装置及其控制系统研究[D]. 哈尔滨:哈尔滨工业大学,2002.
[ 8 ] Shuyu L. Sandwiched piezoelectric ultrasonic transducers of longitudinal-torsional compound vibrational modes[J]. IEEE Ultrasonics, Ferroelectrics and Frequency Control, 1997, 44(6): 1189-1197.
[ 9 ] 张建富,冯平法,申昊,等. 超磁致伸缩纵-扭复合振动超声换能器[P]. 中国,CN103203312A. 2013.07. 17.
[10] 皮 钧. 超声复合振动体[P]. 中国, CN200710009459.8, 2008.1.23.
[11] 林书玉. 纵-扭复合振动模式指数型复合超声变幅杆的研究[J]. 应用声学, 1997, 16(5): 42-46.
LIN Shu-yu. Study on the longitudinal-torsional composite mode exponential ultrasonic horns[J]. Journal of Applied Acoustics, 1997, 16(5): 42-46.
[12] Harkness P, Cardoni A, Lucas M. Ultrasonic rock drilling devices using longitudinal-torsional compound vibration[C]//IEEEUltrasonics Symposium, 2009: 2088-2091.
[13] 张晓辉. 颗粒增强铝基复合材料的超声振动钻削机理研究[D]. 焦作:河南理工大学, 2004.
[14] Cardoni A, Harkness P, Lucas M. Ultrasonic rock sampling using longitudinal-torsional vibrations [J]. Physics Procedia, 2010, 3(1): 125-134.
[15] 尚晓江,邱峰,赵海峰,等. ANSYS结构有限元高级分析方法与范例应用[M].2版.北京:中国水利水电出版社,2008.
Design of a longitudinal-torsional composite ultrasonic vibration machining system and its natural frequencies merging
YUANSong-mei1,2,LIUMing1,2(1. School of Mechanical Engineering & Automation, Beihang University, Beijing 100191, China;2. Beijing Engineering Technological Research Center of High-efficient & Green CNC Machining Process and Equipment, Beijing 100191, China)
Abstract:Longitudinal-torsional composite ultrasonic vibration machining technique attracts more and more attentions in hard and brittle materials machining, for this kind of requirement, a longitudinal-torsional composite ultrasonic vibration machining system was designed, the frequencies merging problem existing in this kind of system was studied based on the finite element analysis. An ultrasonic transducer and a composite horn were designed using the numerical analysis method. After-ward, helical slots were made on the horn, parts of its longitudinal vibrations were converted into its torsional vibrations. Based on the principle that “the closer the longitudinal natural frequencies and the torsional natural ones, the better the results”, the offects of the system’s parameters on its longitudinal natural frequencies and torsional natural ones were analyzed with a finite element analysis software to realize its natural frequencies merging. At last, the system’s modal analysis and transient dynamic analysis showed that the system can realize longitudinal-torsional composite ultrasonic vibration, the effectiveness and applicability of this kind of frequencies merging method are verified.
Key words:longitudinal-torsional composite ultrasonic vibration; helical slots; frequencies merging; finite element analysis
中图分类号:TH122;TH113.1
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.05.002
收稿日期:2015-01-16修改稿收到日期:2015-03-12
基金项目:国家高技术研究发展计划(863计划)(2013AA040105)
第一作者 袁松梅 女,博士,教授,1971年2月生

