橡胶输送带恢复力模型辨识与参数预测
陈洪月 白杨溪 张 瑜 邓文浩
1.辽宁工程技术大学,阜新,1230002.国家地方联合矿山液压技术与装备工程研究中心,阜新,1230003.宾夕法尼亚大学,费城,宾夕法尼亚,19104
橡胶输送带恢复力模型辨识与参数预测
陈洪月1,2白杨溪1张瑜1邓文浩3
1.辽宁工程技术大学,阜新,1230002.国家地方联合矿山液压技术与装备工程研究中心,阜新,1230003.宾夕法尼亚大学,费城,宾夕法尼亚,19104
摘要:橡胶输送带恢复力模型辨识及其参数识别是研究输送带迟滞能耗的关键问题。提出采用高斯函数描述恢复力模型,并采用理论与实验研究相结合的方法分析和验证了高斯函数描述恢复力的可行性及准确性;以实验数据和拟合数据为训练样本,采用经果蝇算法优化后的RBF神经网络对不同激励下恢复力模型系数进行预测,再通过实验对预测结果的准确性进行了验证。
关键词:输送带;迟滞特性;高斯函数;参数识别;果蝇优化算法
0引言
橡胶输送带是输送机的重要组成部分,是由橡胶覆盖层和内部钢丝绳(或纤维)组成的复合材料,受输送机工作负载的影响,输送带受到交变载荷时,由于应变与应力不同相会呈现迟滞效应,并产生能量耗散[1],对于长距离带式输送机而言,输送带的迟滞能耗已经成为输送机的主要运行能耗[2],因此,研究橡胶输送带迟滞特性对研究节能型输送机具有重要意义。
国内外对输送带及其类似材料的恢复力模型研究有:文献[3-4]根据迟滞环面积对输送带的黏滞系数等参数进行了分析和测试;文献[5]采用摩擦学理论和泊松分布建立了金属橡胶的恢复力模型;文献[6]采用等效黏性阻尼理论和实验相结合方法,建立了由高阶非线性多项式和等效的黏性阻尼力叠加而成的金属橡胶的恢复力模型;文献[7]通过对橡胶动态力学实验数据的总结,指出动态力学特性与橡胶结构使用性能和设计之间的关系;文献[8]改进了M-RT模型,研究了丁基橡胶黏弹阻尼材料的动态特性并进行了实验验证;文献[9]采用标准线性固有模型描述了输送带覆盖层的黏弹性;文献[10]提出了采用傅里叶级数来描述金属橡胶的广义恢复力模型;文献[11-12]采用幂函数多项式描述了钢轨扣件减振橡胶的动态力学模型;文献[13]采用BP网络对金属橡胶材料非线性本构关系进行了预估;文献[14]预测了金属橡胶非成形方向的加载和卸载过程迟滞力学特性;文献[15]采用ABAQUS对橡胶的力学性能进行了模拟仿真研究;文献[16]通过假设黏弹性模型的迟滞回路面积不变,加载和卸载过程的压应力、压应变具有线性关系,研究了输送带的运行能耗。
本文采用高斯函数与果蝇优化算法优化后的径向基函数(RBF)神经网络对橡胶输送带的恢复力进行了辨识和预测。首先对傅里叶级数和高斯函数的级数展开表达式进行了对比,分析了采用高斯函数描述非线性恢复力模型的可行性;然后采用高斯函数对输送带的恢复力进行了拟合,并通过实验对恢复力模型的精度进行了验证;再利用高斯函数对不同载荷下的实验数据进行了拟合,以获得用于训练神经网络的数据样本,采用果蝇优化算法对RBF神经网络进行了全局优化,利用优化后的RBF对非线性弹性恢复力的模型参数进行了辨识和预测;最后通过实验对模型预测结果进行了验证。
1输送带非线性恢复力模型
由文献[10-12]可知:输送带的恢复力F可以由非线性弹性恢复力Fk和非线性阻尼力Fc叠加组成,其中恢复力Fk可用傅里叶级数来描述,阻尼力Fc采用椭圆函数来描述,即
(1)
式中,a0、am、bm为描述恢复力的系数;x为激励位移;x0为施加的初始位移;ω为加载频率;A为外加激励振幅;E为输送带在一个循环加载周期内的能量耗散值。
将Fk进行级数展开得
(2)
展开后得
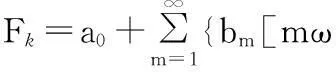
(3)
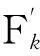
(4)
式中,a、b、c为待识别系数;τ为一个循环加载周期内与激励位移对应的等效时间变量。
式(4)展开成级数形式如下:
(5)
由二项式定理可得
(6)
对比式(3)与式(6)可以看出:两式展开后分别为时间t和τ的幂级数,表达形式相近,说明利用高斯函数替代傅里叶级数来描述非线性弹性恢复力具有可行性;由文献[11-12]可知:当采用傅里叶级数描述恢复力时,项数m越大,拟合精度越高,但需要辨识的系数的数量也越多,为2m+1个,所以采用傅里叶级数描述恢复力时,所需辨识的系数最少为3个,这时模型的辨识精度相对也是最低的;由式(4)可知:采用高斯函数辨识恢复力时,所需辨识的系数只有a、b、c三项,但其级数展开项n却可达到无穷项。综上所述,采用高斯函数描述恢复力时,仅用3个辨识系数,就可达到高阶傅里叶级数的辨识效果,故令输送带的恢复力F描述为
(7)
2恢复力模型精度验证
2.1输送带力学参数测试
为确定式(7)中恢复力模型中的待识别系数并验证高斯函数的拟合精度,采用电子万能实验台对输送带进行动态加载实验。选用st1600型橡胶输送带作为试件,带长1100 mm,两夹具中间的输送带自由段为1000 mm,带宽75 mm,厚度为17 mm,输送带的上覆盖层橡胶厚度为6 mm,下覆盖层橡胶厚度为6 mm,钢丝绳直径为5 mm。实验过程中对输送带施加正弦位移荷载x(t)=Asinωt+x0,其中,A为加载振幅,ω为加载频率,x0为初始位移。
输送带工况下的主频率很小,故将实验中加载频率设定为0.1 Hz,将振幅设定为1.25 mm,初始位移设定为1.75 mm,实验环境温度为18°,实验装置如图1所示。

图1 实验照片
2.2参数识别与精度验证
采用MATLAB对输送带的恢复力模型的参数进行识别,可得恢复力模型中待识别系数a=6519 N、b=2.301 N、c=2.863 N,从而得到当输送带负载为x(t)=1.25sin0.1t+1.75时,弹性恢复力
(8)
由于实验中采用正弦加载,所以式(8)中等效时间变量:
(9)
恢复力拟合曲线与实验曲线如图2所示,两者的确定性系数为0.9992,说明两条曲线吻合良好。将实验值减去拟合值,可得恢复力误差曲线如图3所示,加载阶段的误差绝对值要大于卸载阶段的误差绝对值,最大误差约为120 N、误差均方根为61.88 N,误差相对较小。实验结果表明:采用高斯函数能够较好地描述输送带的非线性恢复力。
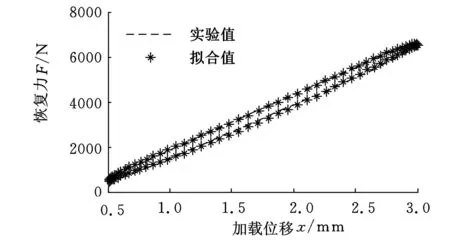
图2 恢复力实验曲线与拟合曲线
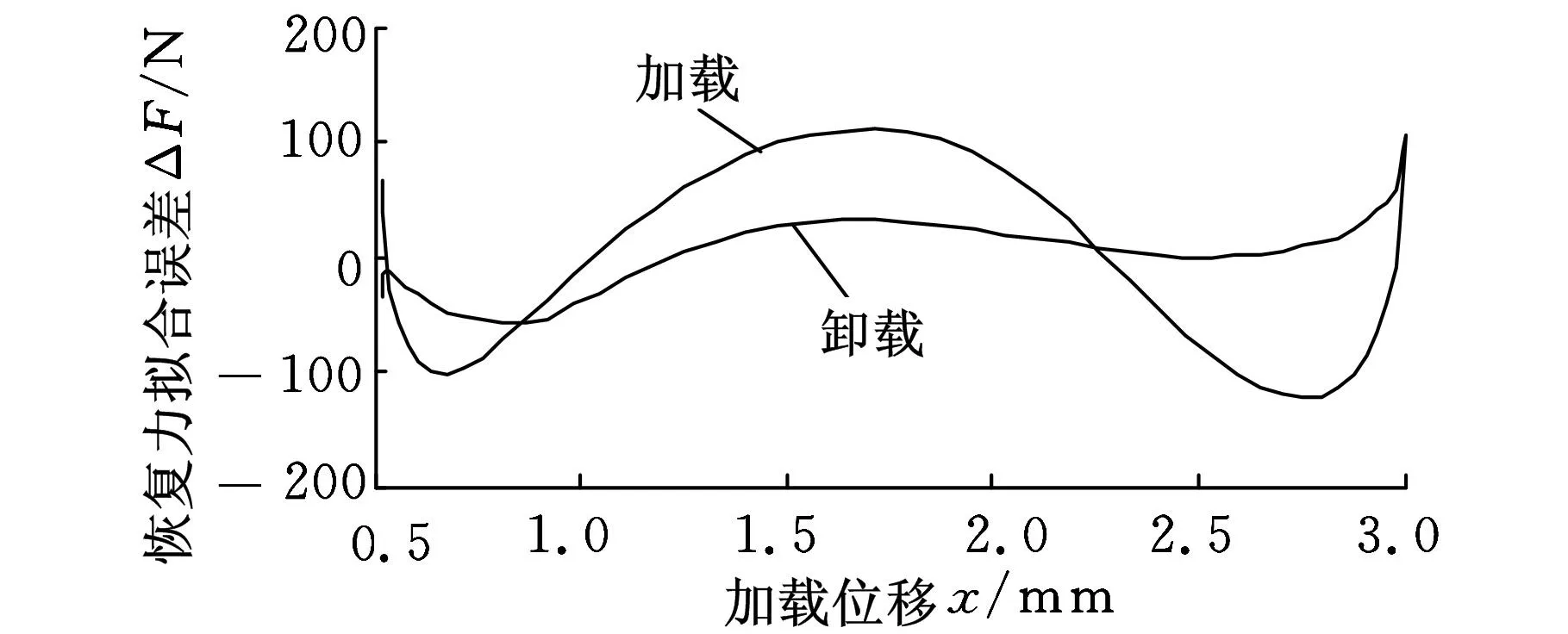
图3 恢复力实验值与拟合值误差
3弹性恢复力模型辨识与精度验证
为预测输送带恢复力模型中的未知参数,建立一个包含果蝇优化算法(FOA)的RBF神经网络[19-22],其中,输入层、输出层、隐含层的节点数分别为3、3、10,网络程序框图如图4所示。
训练样本通过实验测试与MATLAB拟合相结合的方法获得,其中,输入为外加激励的初始值、幅值、频率,输出为MATLAB所拟合的恢复力模型中的系数a、b、c,样本输入值、样本输出值如表1、表2所示。
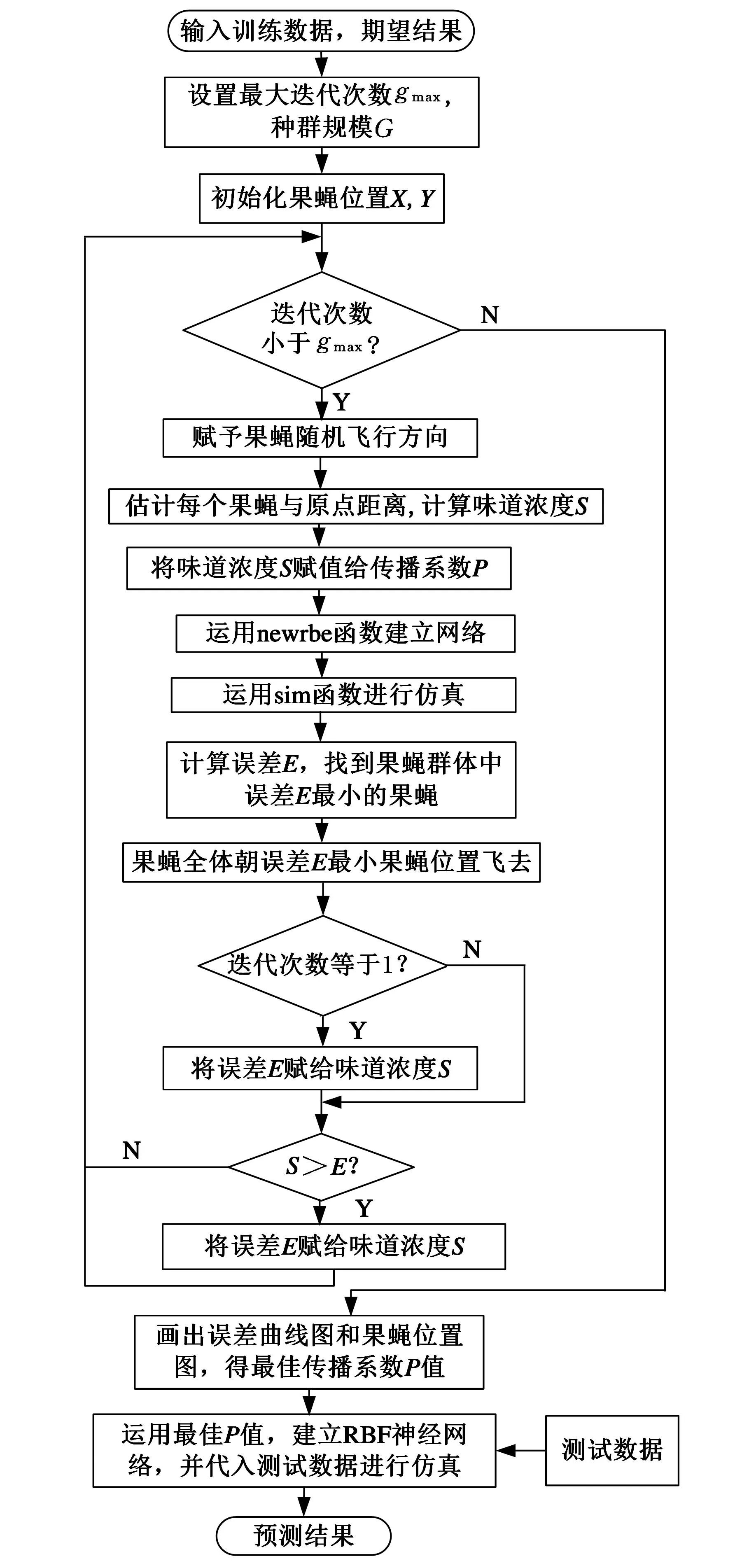
图4 果蝇优化与RBF预测框图
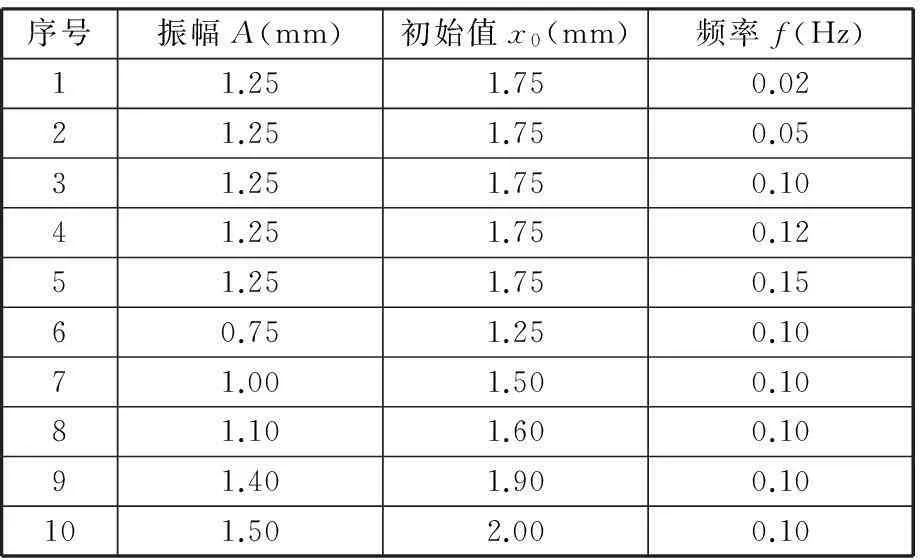
序号振幅A(mm)初始值x0(mm)频率f(Hz)11.251.750.0221.251.750.0531.251.750.1041.251.750.1251.251.750.1560.751.250.1071.001.500.1081.101.600.1091.401.900.10101.502.000.10
设置果蝇优化算法的迭代次数为50,果蝇规模为18,图5所示为果蝇优化算法迭代过程中恢复力的标准误差(RMSE)值,其中当迭代18次时,标准误差达到了4.9238×10-8N,获得的最佳传播系数P值为0.0303,果蝇的搜寻路径如图6所示。
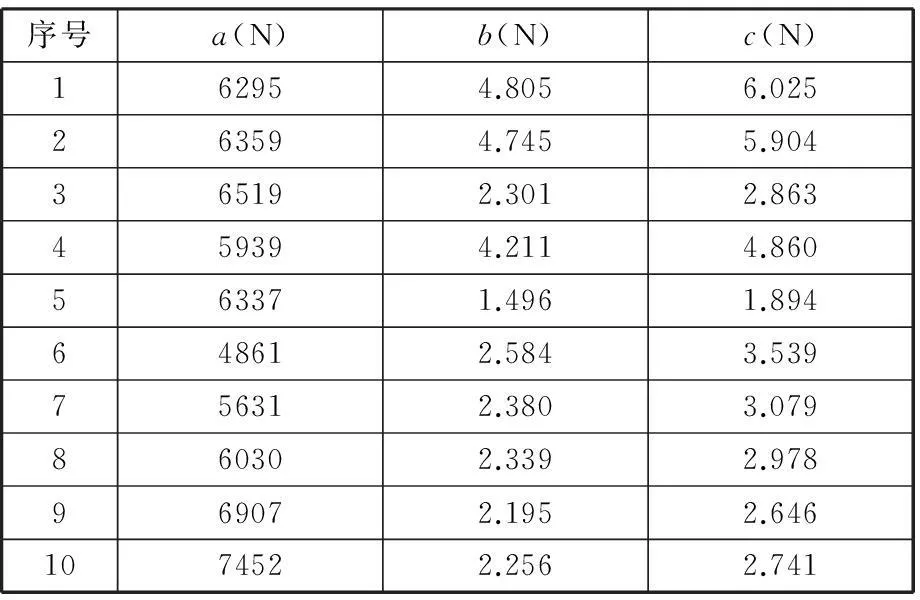
表2 样本输出值
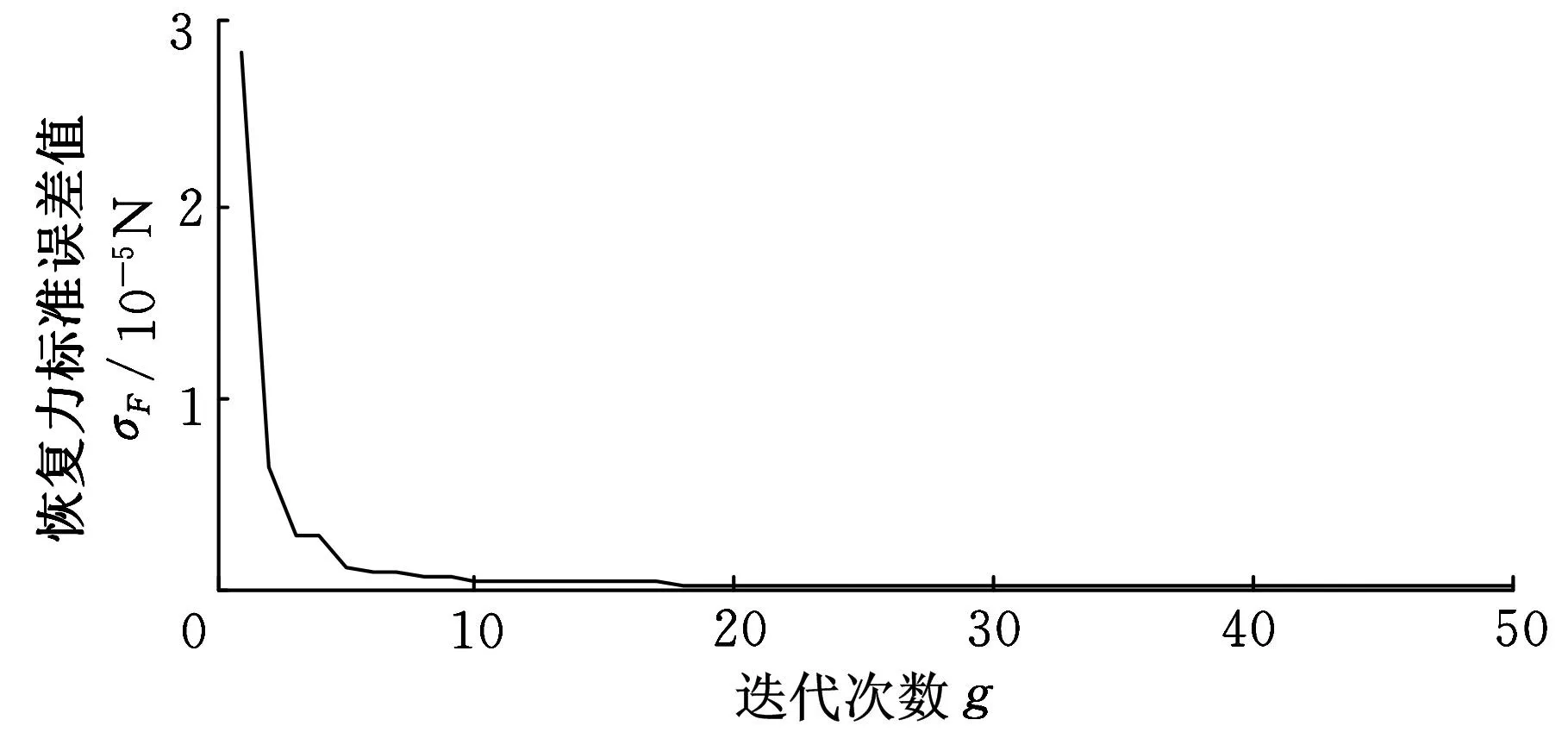
图5 不同迭代次数下恢复力的标准差
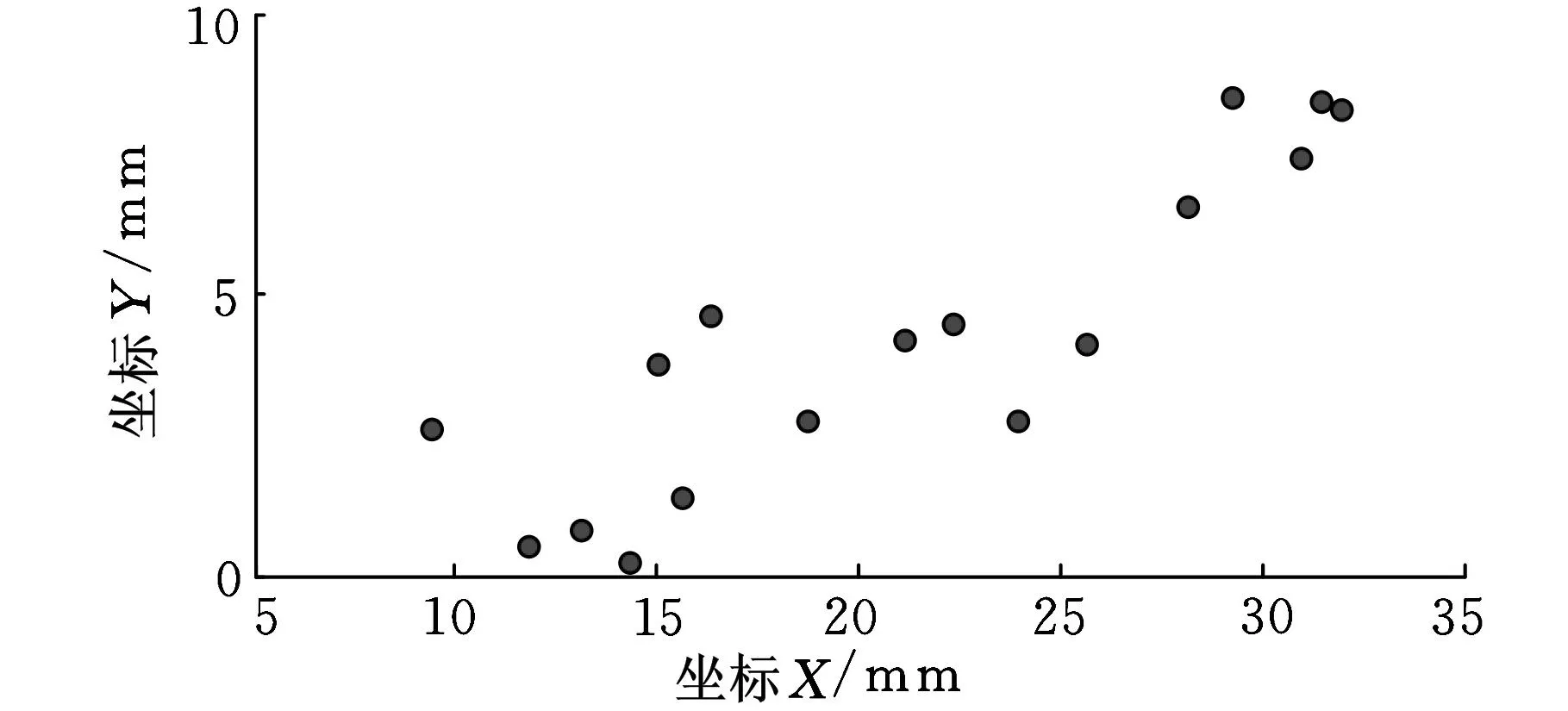
图6 果蝇搜寻路径
为了验证网络预测参数的准确性,抽取一组初始位移x0为2.05 mm、振幅A为1.55 mm、频率ω为0.09 Hz的实验数据进行验证,将x0、A、ω输入到已被果蝇算法优化的RBF模型中,可得到对于该激励下输送带的恢复力模型系数:a=8002 N、b=2.733 N、c=3.354 N,将其代入式(7)可得
预测模型曲线与实验曲线的对比如图7所示,两者吻合程度良好。
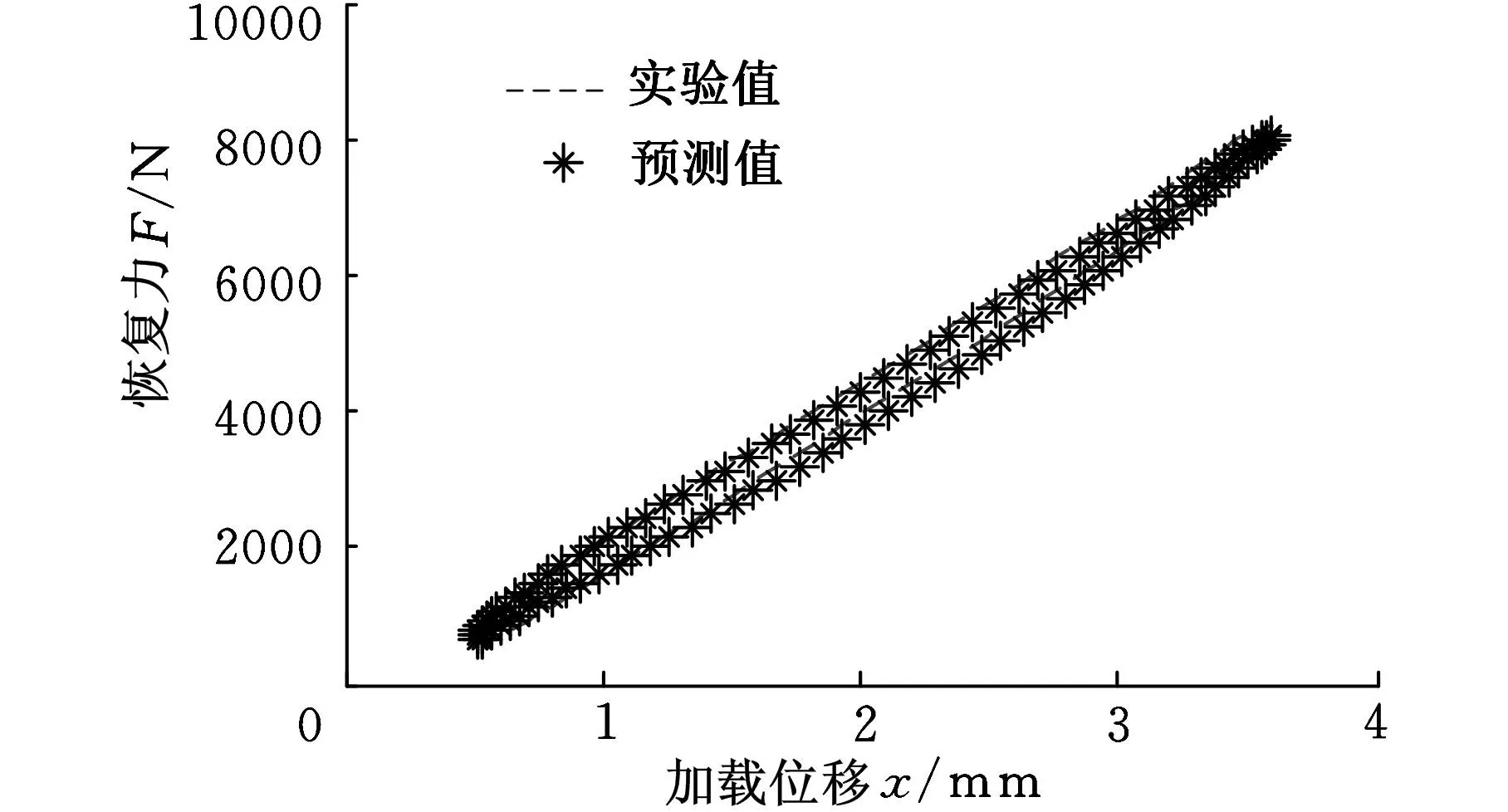
图7 恢复力预测值与实验值
再次采用MATLAB对所抽取的实验数据进行拟合,可得恢复力模型的拟合系数,将其与神经网络预测所得的系数进行对比,结果如表3所示,拟合结果与预测结果较为接近,由此可说明:RBF所预测的恢复力模型系数结果较为准确。

表3 拟合结果与预测结果对比
4结论
(1)采用高斯函数建立了橡胶输送带的非线性恢复力模型,通过实验对模型的辨识精度进行了验证,结果表明:辨识曲线与实验曲线的确定性系数达到了0.9992,证明恢复力模型具有一定的辨识精度。
(2)采用果蝇优化算法和RBF神经网络对输送带的恢复力模型系数进行了预测,通过对比预测曲线与实验曲线,验证了预测结果的准确性。
参考文献:
[1]杨彩红,毛君,李春林.输送带压陷阻力的研究[J],煤炭学报,2010,35(1):149-454.
Yang Caihong,Mao Jun,Li Chunlin.Study of Indentation Resistance of Conveyor Belt[J].Journal of China Coal Society,2010,35(1):149-454.
[2]Lodewijks G.The Rolling Resistance of Conveyor Belts[J].Bulk Solids Handling,1995,15(1):15-22.
[3]刘月琴,孙连生,黄松元.输送带力学性能参数测试方法的研究[J].橡胶工业,1994(41):174-177.
Liu Yueqing,Sun Liansheng,Huang Songyuan.Study on the Conveyor Belt Mechanical Properties Test Method[J].Rubber Industry,1994(41):174-177.
[4]韩刚.输送带粘弹特性的讨论[C]//第一届国际机械工程学术会议.上海,2001:432-436.
[5]敖宏瑞,姜洪源,夏宇宏.金属橡胶弹性迟滞回线的一种新的建模方法[J].中国矿业大学学报,2004,33(4):453-459.
Ao Hongrui,Jiang Hongyuan,Xia Yuhong.Simplified Description Method of Elasto-hysteresis Loop of Metal Rubber Material[J].Journal of China University of Mining & Technology,2004,33(4):453-459.
[6]李宇明,彭威,白鸿柏,等.金属橡胶材料宏观和细观力学模型[J].机械工程学报,2005,41(9):38-42.
Li Yuming,Peng Wei,Bai Hongbai,et al.Mechanical Mode Lof Metal Rubber Material in Macro and Micro Level[J].Journal of Mechanical Engineering,2005,41(9):38-42.
[7]危银涛,杨挺青.黏弹性橡胶动态力学性能与能耗[C]//中国力学学会学术大会.北京,2005:406.
[8]林松,高庆.黏弹阻尼材料动态本构关系研究[J].原子能科学技术,2008,42(12):584-588.
Lin Song,Gao Qing.Dynamic Constitutive Study for VisoelasticDamping Material[J].Atomic Energy Science and Technology,2008,42(12):584-588.
[9]王繁生.带式输送机柔性多体动力学分析方法研究[D].徐州:中国矿业大学,2010.
[10]郝慧荣,白鸿柏,候军芳. 金属橡胶广义恢复力模型辨识[J]. 振动与冲击,2008,27(11):105-110.
Hao Huirong,Bai Hongbai,Hou Junfang.Generalized Resuming Force Model for Metal Rubber[J].Journal of Vibration and Shock,2008,27(11):105-110.
[11]刘艳,罗雁云.钢轨扣件减振橡胶动态特性分析[J].中南大学学报,2011,42(9):2875-2881
Liu Yan,Luo Yanyun.Dynamic Characteristic Analysis of Rubber Absorber in Rail Fastening[J].Journal of Central South University,2011,42(9):2875-2881.
[12]李莉,王书卫,吕英康. 钢轨扣件减振橡胶动态刚度特性分析[J]. 同济大学学报,2013,41(2):208-213.
Li Li,Wang Shuwei,Lü Yingkang.Dynamic Stiffness Analysis of Rubber Absorber in Rail Fastenings[J].Journal of Tongji University,2013,41(2):208-213.
[13]李宇燕,黄协清,李福林.基于BP神经网络的金属橡胶本构关系的预估方法[J].航空动力学报,2011,26(5):1128-1135.
Li Yuyan,Huang Xieqing,Li Fulin.Prediction for Constitutive Relationship of Metallic Rubber Based on BP Neural Net[J].Journal of Aerospace Power,2011,26(5):1128-1135.
[14]曹凤利,白鸿柏,李冬伟,等.金属橡胶非成形方向迟滞特性力学模型研究[J].机械工程学报,2015,51(2):84-90.
Cao Fengli,Bai Hongbai,Li Dongwei,et al.Research on Mechanical Model of Metal Rubber for Hysteresis Characteristic in the Non-forming Direction[J].Journal of Mechanical Engineering,2015,51(2):84-90.
[15]Ghoreishy M H R,Firouzbakht M,Naderi G.Hysteresis Hysteresis Loops Reinforcement Rubber Viscoelasticity[J].Materials and Design,2014,53:457-465.
[16]Spaans C.The Calculation of the Main Resistance of Belt Conveyors[J].Bulk Solids Handling,1991,11(4):145-152.
[17]李敏,盛毅.高斯拟合算法在光谱建模中的应用研究[J].光谱学与光谱分析,2008,28(10):2354-2358.
Li Min,Sheng Yi.Study on Application of Gaussian Fitting Algorithm to Building Model of Spectral Analysis[J].Spectroscopy and Spectral Analysis,2008,28(10):2354-2358.
[18]程诚,黄亚继,孙宇,等.高斯拟合在污泥热重曲线解析中的应用[J].中南大学学报(自然科学版),2014,45(11):4081-4087.
Cheng Cheng,Huang Yaji,Sun Yu,et al.Application of Gaussian Fitting in Resolution of Sludge Thermo-gravimetric Curves Analyzing[J].Journal of Central South University(Science and Technology),2014,45(11):4081-4087.
[19]Pan W T.A New Fruit Fly Optimization Algorithm:Taking the Financial Distress Model as an Example[J].Knowledge-based Systems,2012,26(1): 69-74.
[20]孙立,董君伊,李东海.基于果蝇算法的过热汽温自抗扰优化控制[J].清华大学学报(自然科学版),2014,54(10):1288-1293.
Sun Li,Dong Junyi,Li Donghai.Active Disturbance Rejection Control for Superheated Steam Boiler Temperatures Using the Fruit Fly Algorithm[J].J Tsinghua Univ.(Sci. & Technol.),2014,54(10):1288-1293.
[21]毛正阳,方群,李克行.应用改进果蝇优化算法的月面巡视器路径规划[J].中国空间科学技术,2014,10(5):87-94.
Mao Zhengyang,Fang Qun,Li Kexing.Path Planning for Lunar Rover Based on Modified Fruit Fly Optimization Algorithm[J].Chinese Space Science and Technology,2014,10(5):87-94.
[22]许智慧,王福林,孙丹丹. 基于FOA-RBF神经网络的外贸出口预测[J].数学的实践与认识,2012,42(13):14-19.
Xu Zhihui,Wang Fulin,Sun Dandan.A Forecast of Export Wades Based on the FOARBF Neural Network[J].Mathematics in Practice and Theory,2012,42(13):14-19.
(编辑王艳丽)
Model Identification and Parameter Forecasting of Rubber Conveyor Belt Restoring Force
Chen Hongyue1,2Bai Yangxi1Zhang Yu1Deng Wenhao3
1.Liaoning Technical University,Fuxin,Liaoning,123000 2.National and Local Combined Mining Technology and Equipment Engineering Research Center,Fuxin,Liaoning,123000 3.University of Pennsylvania,Philadelphia, Pennsylvania,19104
Abstract:Model identification and parameter identification of a rubber conveyor belt restoring force were the key problems for researching on hysteresis energy of conveyor belt. The Gaussian function was used to describe restoring force model, its feasibility and accuracy were analyzed and verified by using the method of theory combined with tests.The test and fitting data were treated as training sample. The restoring force model coefficient under different excitations was forecasted by using radical basis function neural network which was optimized by the drosophila algorithm. The prediction accuracy was verified by experiments.
Key words:belt;hysteretic characteristic;Gaussian function;parameter identification; drosophila optimization algorithm
作者简介:陈洪月,男,1982年生。辽宁工程技术大学机械工程学院副教授、博士。主要研究方向为机械系统动态特性。白杨溪,女,1992年生。辽宁工程技术大学机械工程学院硕士研究生。张瑜,男,1987年生。辽宁工程技术大学机械工程学院博士研究生。邓文浩,男,1991年生。宾夕法尼亚大学工程与应用科学学院硕士研究生。
中图分类号:TB33
DOI:10.3969/j.issn.1004-132X.2016.06.019
基金项目:国家自然科学基金资助项目(51304107)
收稿日期:2015-05-05

