基于投票极限学习机的人脸识别混合算法研究

陈铁军，蔡金收，郭　丽

(郑州大学 电气工程学院，河南 郑州 450001)



基于投票极限学习机的人脸识别混合算法研究

陈铁军，蔡金收，郭丽

(郑州大学 电气工程学院，河南 郑州 450001)

摘要：针对小波分析在处理多维图形时不能充分利用数据本身特有几何特征的缺陷，使用第二代曲波变换(the second generation of curvelet transform, SGCT)方法进行人脸图像的处理，选取具有最大标准差的尺度层系数，以完成对人脸图像的特征提取，同时结合基于双向二维主成分分析(bidirectional two dimensional principal component analysis, B2DPCA)的数据降维，构造一种基于混合投票机制极限学习机(voting extreme learning machine,VELM)的人脸识别算法.通过与其他算法的分类结果对比，证明该算法具有更高的识别正确率.

关键词：曲波变换；B2DPCA；投票；ELM；人脸识别

0引言

随着计算机技术模式识别领域的不断发展，生物特征识别技术得到越来越多的关注.而其中的人脸识别技术正因其易于接受、采集方便等特点广泛应用于安全验证系统、视频会议、人机交互、公安系统[1]等领域，人脸识别方法的研究成为模式识别和人工智能的一个重要方面.

人脸识别的技术很多，如基于面部几何特征的方法、基于模板匹配的方法、基于子空间分析的方法，另外还有基于神经网络、支持向量机和变换域的方法[2]等.其中变换域方法中的小波变换，其变换系数不仅能反映对应频率分量的强度，而且也能反映其时间位置，即能提供精准的时域定位和频域定位[3]，因此广泛应用于人脸特征的提取.文献[4-7]介绍了多种将小波变换与其他方法相结合的人脸识别算法.

由于二维可分离小波仅能表示一维数据的点奇异性，不能最优地表示二维图像的奇异曲线[2]，而曲波变换不仅具有小波变换的多分辨率特性和时频局域特性，还具有非常强的方向性和各向异性[8]，可以很好地提取二维图像的几何特征，保持对曲线的敏感性和对二维图像奇异曲线的跟踪，并将图像分解为不同尺度、不同方向的层次，因而受到广泛关注.利用曲波变换实现图像分解，结合主成分分析、二维主成分分析或者核主成分分析对人脸或其他研究对象特征进行降维，进而可使用神经网络(neutral network, NN)、BP神经网络(back propagation neutral network, BPNN)进行分类[9-11].该类方法在分类时存在不同程度的学习速度慢及泛化能力较弱的缺陷，且需人为设置大量的网络训练参数，很容易产生局部最优解.

综上所述，为了充分利用曲波变换的图像分解结果，最大程度地利用图像有效信息,降低数据维度，实现人脸的快速识别分类.笔者将曲波变换和双向二维主成分分析相结合，然后使用基于投票机制的极限学习机进行分类，继而使用人脸数据库ORL、Yale等进行试验，并将该算法与其他使用基本手段的算法进行比较.

1算法描述

1.1曲波变换

曲波变换用来将图像映射到多尺度多方向上，图像的信息包含在变换后所得的各尺度层系数中.第二代曲波变换是曲波变换的一种快速算法，笔者用到的是快速离散曲波变换(fast discrete curvelet transform,FDCT).FDCT有两种实现方法：USFFT和Wrap算法[13].Wrap算法比USFFT算法去噪效果更好，且运行速度较高，故笔者选用Wrap算法.Wrap算法的主要思想是围绕原点Wrap计算，在对任一区域实现时，需要用周期化技术映射到原点的放射区域中，且具有一一对应的映射关系.

通过Wrap算法进行曲波变换，并计算各层系数标准差，选定具有最大标准差的尺度层系数作为特征脸，保留原有大部分图像信息，以产生初始特征向量，并以最小的混叠影响加强高频成分定位.下面以人脸库中选定个体图像为例进行曲波变换系数分析.其中参数设置为3个尺度层、8个角度方向，经过对图像进行曲波变换，得到变换后的曲波系数.即原始图像经傅里叶变换后变换到频域，按频率可将图像分为3个部分[14]：Coarse层、Detail层和Fine层.Coarse层包含的是最内层低频系数；Detail层包含中间层的中高频系数；Fine层包含最外层的高频系数.表1分别给出了ORL及Yale人脸库中的第一个个体图像的各层系数标准差，包含Coarse层、Fine层和Detail层8个角度.结果表明：低频系数标准差最大，远大于其他各层、各角度的标准差，它包含了图像概貌.其中图1为原始图像、Coarse层及Fine层系数重构图像，图2给出了Detail层中任选4个角度的系数重构图像.从图1和图2给出的原始图像及各层重构图像也可知，Coarse层最能表示图像的概况，而Fine层表示的是图像高频轮廓信息.故Coarse层尺度系数作为B2DPCA的特征输入数据是合理的.

表1　不同数据库各层平均标准差

图1　原始图像、Coarse层及Fine层重构图

图2　Detail层系数4个方向系数重构图

1.2双向二维主成分分析(B2DPCA)

B2DPCA由YANG等人提出[15]，是2DPCA的改进算法，它克服了2DPCA在表示图像时需要更多的协同系数、不利于图像数据存取的弱点.其主要思想是在行和列2个方向上各执行1次2DPAC运算，大大消除了人脸图像行和列的相关度.运用新准则选取了更适合于分类的主分量，大大压缩特征的维数，将其应用于人脸识别，可减少计算复杂度，同时提高分类速度.B2DPCA是在2DPCA算法的基础上实现的，处理过程如图3所示.

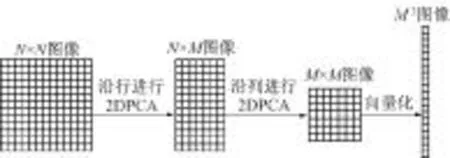
图3　B2DPCA处理过程

1.3投票机制的极限学习机(VELM)

传统优化技术的学习速度很慢，为克服这一缺点，黄广斌等[16]提出了一种单隐层前馈神经网络极限学习机.极限学习机参数设置简单，求解直接，并具有学习速度快且泛化性能好等优点.但ELM的隐节点随机设定，并且在训练过程中保持不变，因此会导致错误划分.为降低错误划分几率,文献[17]中提出了一种投票机制的极限学习机.使用多个具有相同隐层节点和相同激活函数的单个极限学习机进行训练，而其学习参数是随机独立初始化的.测试结果为投票数最多的类标签.

如VELM中有K个独立ELM，隐节点均设为L，激活函数相同，随机初始化学习参数，利用所有的训练样本对每个ELM进行训练，得出输出权值；对于一个测试样本，用每个训练过的ELM进行测试，得出K个预测结果，相同的结果累计记录，最后将投票最多的类标签视为该测试样本的分类结果.该算法过程伪代码如表2所示.

表2　VELM算法

2人脸数据库简介

ORL人脸库由英国剑桥Olivetti实验室拍摄的一系列人脸图像组成，共有40个不同年龄、不同性别和不同种族的被拍对象.每个对象有10幅图像，共计400幅，图像尺寸是92×112，图像背景为黑色.其中人脸部分表情、细节和姿态均有变化，其深度旋转和平面旋转可达20°，人脸尺寸也有最多10%的变化.该库是目前使用最广泛的标准数据库，它含有大量的比较结果.

Yale数据库由耶鲁大学计算视觉与控制中心创建，包含15位志愿者的165张图片，包含光照、表情和姿态的变化.图像尺寸是100×100.FERET人脸库由FERET项目创建，包含14 051张多姿态，均为带光照的灰度人脸图像，是人脸识别领域应用最广泛的人脸数据库之一.其中多数人是西方人，每个人所包含的人脸图像的变化比较单一.除此之外，GTech也是常用人脸库之一.

3实验设置及结果分析

3.1实验设置

先读取所有图像，将其灰度化处理，维度缩放为原来的一半；继而进行曲波变换时的参数设置：尺度层为3、角度方向为8个，获得曲波系数；取Coarse层系数进行B2DPCA运算，获得维数压缩后的特征向量；分别取50%作为训练样本，50%作为测试样本，当个体拥有图像数目为奇数时，取中间数作为训练样本个数；所有样本进行归一化处理，激活函数选取sigmoid.其中ELM的第一层权值为随机产生，其个数和隐层节点数通过实验来确定.

下面以ORL数据库为例进行实验，并取运行10次的平均结果进行分析，如图4所示.由图4可知，隐节点数从100开始递增时，精度提高较大，超过700后，增幅较小，且将隐节点设置越大，时间开销越多，因此笔者将其设为700.

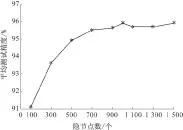
图4　不同隐节点的测试精度

在此基础上对VELM中单个ELM个数的设置进行实验.以700为隐层节点数，图5记录了不同ELM个数下的测试精度.由图5可知，个数大于8后无太大改善.当单个ELM个数增大时，时间开销大大增加，故将其个数设置为8较为合理.

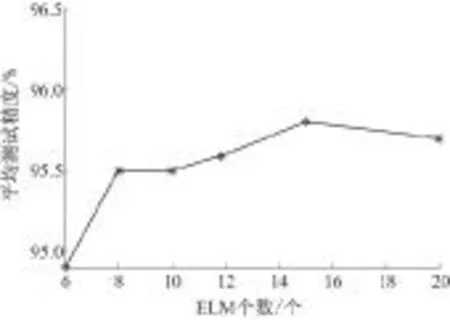
图5　不同ELM个数的测试精度

通过实验对比可得，设定ELM个数和隐层节点数分别为8和700，对比算法有Curvelet+B2DPCA+ELM和Curvelet+2DPCA+VELM；ELM隐层节点数和激活函数与VELM设为一致；所有算法均运行50次取平均分类精度.

3.2实验结果分析

首先通过不同人脸数据库的测试精度和标准差比较3种不同算法的性能，其次将Curvelet+2DPCA+VELM和Curvelet+B2DPCA+ELM的50次测试精度分别与Curvelet+B2DPCA+VELM的精度作Wilcoxon秩和检验，显著性水平设为0.05，以充分比较分类精度的差异性，Wilcoxon秩和检验结果标识于对比算法测试精度后侧，如表3所示.由表3可知，Curvelet+B2DPCA+VELM算法在4个人脸数据库中均取得了最高的测试精度，但与Curvelet+B2DPCA+ELM方法相比，在ORL和Yale人脸库上的测试精度无明显差异，但在RET和GTech上的测试结果中则是胜出的.其中Curvelet+2DPCA+VELM精度最差，4组人脸数据的测试精度均明显低于笔者所提出的算法.由此可见，使用VELM和ELM分类器对分类结果影响不大，而2DPCA和B2DPCA的使用可带来大约5%的精度差，由此可知，B2DPCA的利用在该算法中起到了重要作用.除此之外，从标准差上来看，笔者所提出的方法在测试稳定性方面和另外两个方法相比没有明显差别.

为进一步验证笔者算法的性能，下面将Curvelet+B2DPCA+VELM与基于白化PCA图像重构的特征补偿人脸识别方法(记为WPCAR)[18]进行比较.图像预处理、运行次数及样本选取比例与前文保持一致.对比结果如表4所示.由表4可知，就测试精度而言，WPCAR算法除在RET上的测试精度优于笔者算法外，其余3类测试精度均较差；RET测试上的Wilcoxon秩和检验结果有同样结论，2种算法所得结果差异明显.就标准差而言，除在RET上的标准差两者相同外，笔者算法能够获得更小数值，因此笔者算法具有更高的稳定性.

表3　不同算法的测试精度和标准差

注：精度后“+”、“-”及 ” ≈”分别表示该算法与Curvelet+B2DPCA+VELM相比，有明显差异且好于该算法、有明显差异且次于该算法、无明显差异.

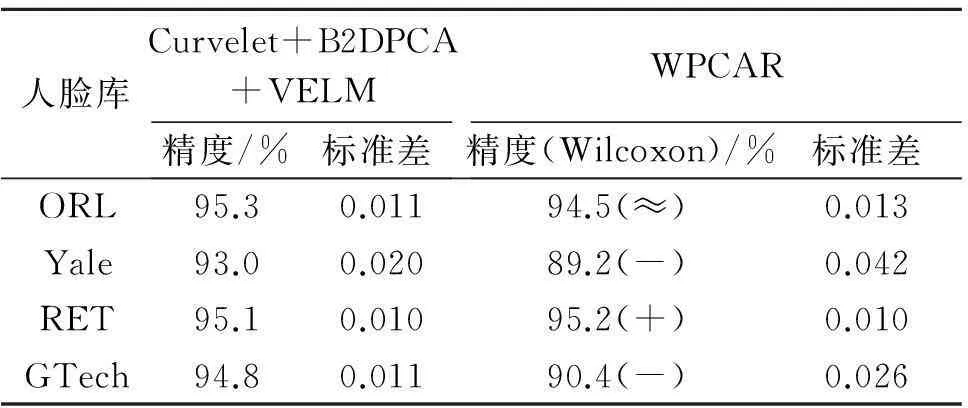
表4　与WPCAR对比结果

4结论

针对小波变换和2DPCA在人脸识别上存在的缺陷，笔者提出了一种将第二代曲波变换、B2DPCA和投票机制的极限学习机相结合的人脸识别算法.通过试验可知，第二代曲波变换对二维及以上图像可以更好地提取其特征，而B2DPCA具有较好的降维效果，且笔者算法在测试精度和稳定性方面整体表现良好.

参考文献：

[1]田晓亮. 基于Gabor小波变换和子空间的人脸识别技术研究[D]. 太原:太原理工大学信息工程学院, 2010.

[2]时培培. 基于第二代曲波变换结合改进子空间技术的人脸识别技术研究[D]. 北京:北京化工大学信息科学与技术学院, 2012.

[3]LIN J, LI J P, JI M. Robust face recognition by wavelet features and model adaptation[C]//Wavelet analysis and pattern recognition, 2007. Piscataway, NJ: IEEE Computer Society, 2007: 1638-1643.

[4]王宪,陆友桃,宋书林,等. 基于Gabor小波变换与分块PCA的人脸识别[J]. 计算机工程与应用, 2012(3): 176-178，231.

[5]王朝阳,达飞鹏. 基于多尺度哈尔小波变换的三维人脸识别方法[J]. 系统仿真学报, 2013(7): 1442-1445.

[6]赵焕利,王玉德,张学志,等. 小波变换和特征加权融合的人脸识别[J]. 中国图象图形学报, 2012(12): 1522-1527.

[7]李孔震,王炳和,娄昊,等. 基于小波变换和二维非负矩阵分解的人脸识别算法[J]. 计算机应用研究, 2013(4): 1275-1277,1280.

[8]贾西贝. 基于曲波变换的人脸识别算法研究[D]. 哈尔滨:哈尔滨工程大学理学院, 2011.

[9]朱世交,张南华. 一种基于曲波变换的手势特征提取新方法[J]. 计算机工程与应用, 2006(33): 50-52.

[10]YE J H, HU D, XIA G M, et al. An advanced BPNN face recognition based on curvelet transform and 2DPCA[C]//Computer science & education, 2013. Piscataway, NJ: IEEE computer society, 2013: 1019-1022.

[11]MA H, HU F S. The study of human face recognition based curvelet transform and 2DPCA[C]//Information science and engineering, 2010. Piscataway, NJ: IEEE computer society, 2010: 5512-5515.

[12]MOHAMMED A A, WU Q M J, SID-AHMED M A. Systems application of bidirectional two-dimensional principal component analysis to curvelet feature based face recognition[C]//Systems, man and cybernetics, 2009. Piscataway, NJ: IEEE computer society, 2009: 4124-4130.

[13]CANDES E, DEMANET L, DONOHO D, et al. Fast discrete curvelet transforms [J]. Multiscale modeling & simulation, 2006, 5(3): 861-899.

[14]赵阳. 曲波变换在人脸识别中的应用[D].西安:西安理工大学自动化与信息工程学院, 2011.

[15]YANG J, ZHANG D. Two-dimensional PCA: a new approach to appearance-based face representation and recognition [J]．IIEEE Trans. PAMI, 2004, 26(1): 131-137.

[16]HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1-3): 489-501.

[17]CAO J W, LIN Z P, HUANG G B, et al. Voting based extreme learning machine [J]. Information sciences, 2012, 185(1): 66-77.

[18]陈素根,尹贺峰. 基于白化PCA图像重构的特征补偿人脸识别新方法[J]. 计算机应用研究, 2015, 32(9): 2853-2856.

Research on Hybrid Face Recognition Algorithm Based on Voting Extreme Learning Machine

CHEN Tiejun, CAI Jinshou, GUO Li

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:In view of the deficiency of wavelet transform that geometrical characteristic of the data can not be fully atilized when multidimensional images’ features are detected, this paper applies the second generation of curvelet transform to process facial images. The procedure extracts images’ features through choosing the subband coefficient with the maximum standard deviation. Then data dimensionality is reduced using the bidirectional two-dimensional principal component analysis (B2DPCA). Combining with the two methods above, this paper constructs a face recognition algorithm based on hybrid voting extreme learning machine(VELM). The experimental results show that the algorithm presents improved performance compared with other algorithms mentioned in terms of recognition accuracy.

Key words:curvelet transform; B2DPCA; voting; ELM; face recognition

中图分类号：TP391.4

文献标志码：A

doi:10.3969/j.issn.1671-6833.201505016

作者简介:陈铁军(1954—)，男，河南信阳人，郑州大学教授，博士，博士生导师，主要从事复杂系统控制与理论研究，E-mail:tchen@zzu.edu.cn.

基金项目：国家自然科学基金资助项目(41174127)；教育部博士点基金资助项目(20114101110005)

收稿日期:2015-05-07；

修订日期：2015-08-11

文章编号:1671-6833(2016)02-0037-05

引用本文：陈铁军，蔡金收，郭丽.基于投票极限学习机的人脸识别混合算法研究[J].郑州大学学报(工学版)，2016,37(2):37-41．