基于发动机磁流变悬置的整车半主动振动控制*

郑 玲,邓召学,庞 剑,徐小敏，付江华,陈代军

(1.汽车噪声振动和安全技术国家重点实验室，重庆 401120； 2.重庆大学，机械传动国家重点实验室，重庆 400030； 3.长安汽车工程研究院，重庆 401120)

2016036

基于发动机磁流变悬置的整车半主动振动控制*

郑 玲1,2,邓召学2,庞 剑1,3,徐小敏1,3，付江华1,3,陈代军1,3

(1.汽车噪声振动和安全技术国家重点实验室，重庆 401120； 2.重庆大学，机械传动国家重点实验室，重庆 400030； 3.长安汽车工程研究院，重庆 401120)

为提高磁流变悬置力学模型的建模精度，改善发动机悬置系统的减振效果，提出以磁流变悬置动态性能试验结果为数据样本，利用Elman神经网络对磁流变悬置的正、逆模型进行模型辨识，并将辨识模型用于悬置系统控制的方法；在同时考虑了随机路面输入和发动机激励的情况下，建立了基于磁流变悬置的整车10自由度动力学模型，以发动机转速和悬置点处的加速度信号为输入，设计了变论域模糊控制器，研究了磁流变悬置的半主动控制性能。仿真结果表明：相对传统的模糊控制，变论域模糊控制器具有较好的宽频隔振效果，悬置点处的振动加速度峰值明显减小，验证了所建模型和变论域模糊控制算法的正确性和有效性。

发动机；磁流变悬置；振动控制；Elman神经网络；变论域模糊控制

前言

汽车发动机磁流变悬置是利用磁流变(magneto-rheology, MR)技术实现阻尼实时控制，具有可控性强、响应速度快和功耗低等优点[1]，在动态特性上更能满足发动机对隔振的要求，成为汽车发动机智能悬置领域的研究热点。磁流变悬置是一种新型的智能可控半主动悬置，通过外加磁场的变化，可实现悬置阻尼力在一定范围内的连续、无级调节[2]，以达到真正意义上的宽频隔振。现阶段发动机磁流变悬置的实际应用尚少，如德尔福推出的GT3发动机。因此研究半主动磁流变悬置有重要的理论价值和广泛的应用前景。

磁流变液压悬置具有较高的非线性和滞回特性[3]等特点。为实现发动机磁流变悬置系统精确控制，建立合理的磁流变悬置正、逆模型成为控制方法研究的基础。目前，常用模型辨识方法主要分参数化模型和非参数化模型两大类[4]。在参数化模型中，Bingham模型简单易于分析，能够很好地表达力-位移特性，但不能描述磁流变阻尼器屈服前特征，即双黏性特征、滞后特性和剪切变稀现象[5-7]。文献[8]中对非线性双黏性模型进行了改进，提出了具有4参数的非线性滞回双黏性模型，但磁流变阻尼器低速区特性仍然难以描述。针对这一问题，文献[9]中提出了现象模型，该模型能较好地模拟磁流变阻尼器低速时的恢复力衰减现象，但模型参数较多，且数学计算较为复杂。神经网络[10]是非参数化模型中最具应用前景的模型辨识方法之一，其具有高度的鲁棒性、自学习能力和非线性映射能力，尤其适用于描述复杂非线性系统，这为建立MR阻尼器的逆模型提供了一条有效的途径。文献[11]中采用模糊自适应理论建立了磁流变阻尼器模型。该模型以阻尼器的位移、速度和控制电压作为模型输入，可控阻尼力为输出，很好地描述了阻尼器的滞回特性，但模型结构复杂，隶属度函数数目多，易出现维数灾难。文献[12]中利用递归神经网络(RNN)对磁流变阻尼器建模，RNN网络以内部状态反馈来描述磁流变阻尼器的非线性特征，但因网络结构复杂，存在训练算法收敛速度慢的问题。

目前，国内外学者对发动机磁流变悬置半主动控制也做了大量研究工作。文献[13]中以减小发动机对基座的垂向传递力为目标，设计了发动机垂直隔振模糊控制器。发动机激励频率和力传递率为模糊控制器的输入量，可调阻尼为输出量，根据发动机激励频率和力传递率的模糊状态，利用建立的模糊规则可以得到悬置的阻尼。文献[14]中以动力总成两端的垂直速度为反馈信号，对悬置的磁场电流进调节，来确定磁流变悬置的阻尼力，设计了半主动天棚控制器，对整车进行振动控制。

本文中以磁流变悬置动态试验数据为训练样本建立了磁流变悬置Elman网络正、逆模型；在考虑了随机路面输入和发动机激励的情况下，建立了基于磁流变悬置的整车10自由度动力学模型，最后通过编写变论域模糊控制S文件实现磁流变悬置系统的半主动控制。仿真结果表明：变论域模糊控制较传统模糊控制具有更好的宽频隔振效果，发动机转速对应的2阶主频加速度振动峰值明显减小，验证了Elman网络模型及其变论域模糊控制算法的正确性和有效性。

1 磁流变悬置结构设计和性能试验

以磁流变液的流变特性为基础，针对某汽车发动机动力总成设计了基于流动模式的阻尼力连续可调的磁流变液压悬置[15]，悬置结构如图1所示。

磁流变液压悬置主要包括橡胶主簧、磁芯组件、励磁线圈和橡胶底膜等。橡胶主簧通过橡胶硫化工艺与上壳体、加强块和连接螺纹杆进行粘接来支撑发动机静载荷，连接螺纹杆通过加强块的中心螺纹与加强块固定连接，上外磁芯、下外磁芯和内磁芯之间构成环形阻尼通道，在发动机载荷作用下，橡胶主簧、加强块和连接螺栓一起上下运动，磁流变液通过阻尼通道在上下液室之间流动，通过控制电磁线圈激励电流的大小来调节设置于磁芯组件内的磁流变液通道的磁感应强度，从而调节该处的磁流变液黏度，进而使悬置具有理想的刚度特性和阻尼特性，以达到良好的隔振效果。

采用MTS综合试验台对自行设计的磁流变悬置进行动态性能测试，如图2所示，试验采集激振幅值为0.2mm和1mm，激振频率范围为1～50Hz，频激振率间隔为1Hz，电流分别为0，0.5和1.0A时的磁流变液压悬置阻尼力数据，为后续磁流变悬置模型的辨识和控制算法的设计奠定基础。

2 Elman神经网络正逆模型

神经网络具有高度的鲁棒性、自学习能力和非线性映射能力，为建立磁流变阻尼器的正、逆模型提供了一条有效的途径。Elman回归神经网络即属于典型的动态神经网络，它在BP神经网络结构的隐含层中增加了一个承接层，作为一步延时的算子，以达到记忆的目的，从而使系统具有适应时变特性的能力，能直接反映动态过程系统的特性，提高网络对复杂非线性的映射能力。

Elman神经网络结构一般分为4层：输入层，隐含层，承接层，输出层。输入层的单元起到信号传输作用，输出层单元起线性加权作用，隐含层单元的传递函数采用线性或非线性函数，承接层用来记忆隐含层单元前一时刻的输出值并返回给网络的输入，认为是一个一步延时算子。Elman网络的非线性状态空间表达式为

y(k)=g(w3x(k))

x(k)=f(w1xe(k)+w2u(k-1))

xe(k)=x(k-1)

式中：y为m维输出节点向量；x为n维隐含层节点单元向量；u为r维输入向量；xe为n维反馈状态向量；w3为隐含层到输出层链接权值；w2为输入层到隐含层连接权值；w1承接层到隐含层的连接权值；g为输出神经元的传递函数，是隐含层输出的线性组合；f为隐含层神经元的传递函数。

Elman神经网络采用BP算法进行权值修正，学习的指标函数采用误差平方和函数。

2.1 Elman神经网络正模型

以磁流变悬置动态性能实验结果作为训练和预测样本，基于Elman神经网络对磁流变悬置正模型进行辨识，如图3所示。该网络输入变量分别是激振位移Sk、控制电流Ik、激振频率fk，网络输出变量为输出阻尼力Fk。

图4为不同电流下，磁流变悬置阻尼力与激励位移关系的试验结果和Elman神经网络正模型预测结果，实线表示试验结果，虚线表示预测结果。从图中可看出，辨识曲线与磁流变悬置性能试验数据趋势一致。图5是Elman神经网络正模型训练均方误差收敛曲线。由图可见，Elman神经网络正模型预测输出阻尼力误差在[-15 10]N范围内，表明Elman神经网络正模型预测结果具有较高的辨识精度。

2.2 Elman神经网络逆模型

同样地，以磁流变悬置动态性能试验结果作为训练和预测样本，基于Elman神经网络对磁流变悬置逆模型进行辨识，如图6所示，该网络输入变量分别是激振位移Sk、输出阻尼力Fk、激振频率fk，网络输出变量为控制电流Ik。

图7为不同试验数据下，磁流变悬置控制电流试验结果和Elman神经网络逆模型预测结果，实线表示控制电流试验结果，虚线表示控制电流预测结果。从图中可以看出，辨识电流大小与磁流变悬置试验数据能够较好的吻合。图8是逆模型训练均方误差收敛曲线。从图中可以看出，Elman神经网络逆模型预测控制电流误差在(-4～2)×10-4A范围内，表明Elman神经网络逆模型预测结果具有较高的辨识精度。

Elman神经网络正逆模型为磁流变悬置半主动控制研究奠定了基础。

为了评价Elman神经网络正、逆模型的逼近精度，建立如下指标[16]：

(1)

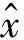
根据式(1)可以得到不同激励频率、不同电流下的相对逼近精度，如表1所示。可以看出：Elman神经网络逆模型的逼近精度高于93%，满足工程需要，表明Elman神经网络在磁流变悬置正、逆模型辨识方面具有高度的辨识能力。

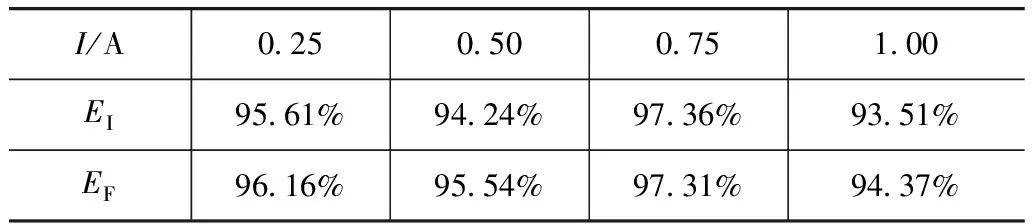
表1 Elman神经网络正、逆模型逼近精度

3 基于磁流变悬置系统的整车半主动控制

汽车动力传动系的扭转振动及路面不平度是引起汽车整车振动的主要原因，为了改善汽车的乘坐舒适性，有必要同时考虑发动机激励和路面不平度的外界干扰，建立汽车整车动力学模型，以研究磁流变半主动悬置系统对汽车整车性能的影响。

3.1 路面输入模型

在随机路面上匀速行驶的车辆，其路面输入模型[17]为

(2)

式中：v(t)为汽车车速；w(t)为零均值高斯白噪声；n0为参考空间频率，n0=0.1m-1；G0为参考空间频率n0下的路面不平度系数，m3。

3.2 基于磁流变悬置的整车动力学模型

图9为基于磁流变悬置系统的整车10自由度动力学模型。将车身视为刚体,考虑发动机的垂向、俯仰、侧倾3个自由度的运动，车身的垂向、侧倾、俯仰3个方向的运动，以及4个轮胎的4个自由度运动。发动机由4点悬置支撑，分别用1，2，3，4表示，其中1号为磁流变悬置，其他为被动橡胶悬置。发动机坐标系原点在发动机质心位置，X轴指向汽车前方，Y轴指向汽车左侧，Z轴由右手定则确定。车身坐标系原点在车身质心处，坐标轴方向与发动机坐标系平行。

(1) 发动机垂向、侧倾和俯仰运动动力学方程

(3)

(2) 车身垂向、侧倾和俯仰运动动力学方程

(4)

式中fbj为各悬架力。

(3) 非簧载质量垂向动力学方程

(5)

当发动机俯仰角和侧倾角较小时，悬置上端4点的垂向位移与发动机坐标原点位移的关系为

(6)

式中：(tei,lei)为悬置上端点相对于发动机坐标系坐标(xei,yei)的绝对值；wi为4个车轮的路面输入干扰。同样可以得到悬置下端4个点和悬架上端4个点的垂向位移与车身坐标原点位移的关系。

令q=[zeθexθeyzbθbxθbyzu1zu2zu3zu4]TU=u1；Fe=[FzFθxFθy]T

整理以上车辆运动方程，可得微分方程的标准形式：

(7)

式中：Mw为质量矩阵；Cw为阻尼矩阵；Kw为刚度矩阵；Bw为悬置可控阻尼力输入矩阵；Dw为发动机激励输入矩阵。

(8)

整车10自由度模型中所用的变量如表2所示。

3.3 变论域模糊控制系统设计

模糊控制理论已广泛应用于工业生产、家用电器、军事等领域,取得了大量的成功实例。传统的模糊控制器输入、输出变量的论域一旦选定，则在整个控制过程中都不能再修正，一旦论域选择偏大或偏小，都将严重影响模糊控制器的控制效果，并且控制器只具有相当于比例和微分的功能，无法在本质上消除系统静差，导致系统在微偏差范围内存在所谓的“控制死区”。模糊控制器本质上是插值器。

针对以上问题，本文中应用变论域模糊控制算法，变论域模糊控制器,就是通过选取合适的论域伸缩因子,以伸缩论域来减小误差对控制系统的影响,越接近期望控制点,控制器的档级越小,使得实际的控制规则大幅度增加,因而获得比较满意的动态和稳态的性能指标。变论域模糊控制能在控制过程中根据系统的输入、输出情况对初始论域进行动态调整，降低了对初始论域的要求；采用变论域模糊控制器时，虽然规则形式不变，但论域收缩使得规则局部细化，相当于增加了模糊规则数目，即插值点加密，从而提高控制精度。

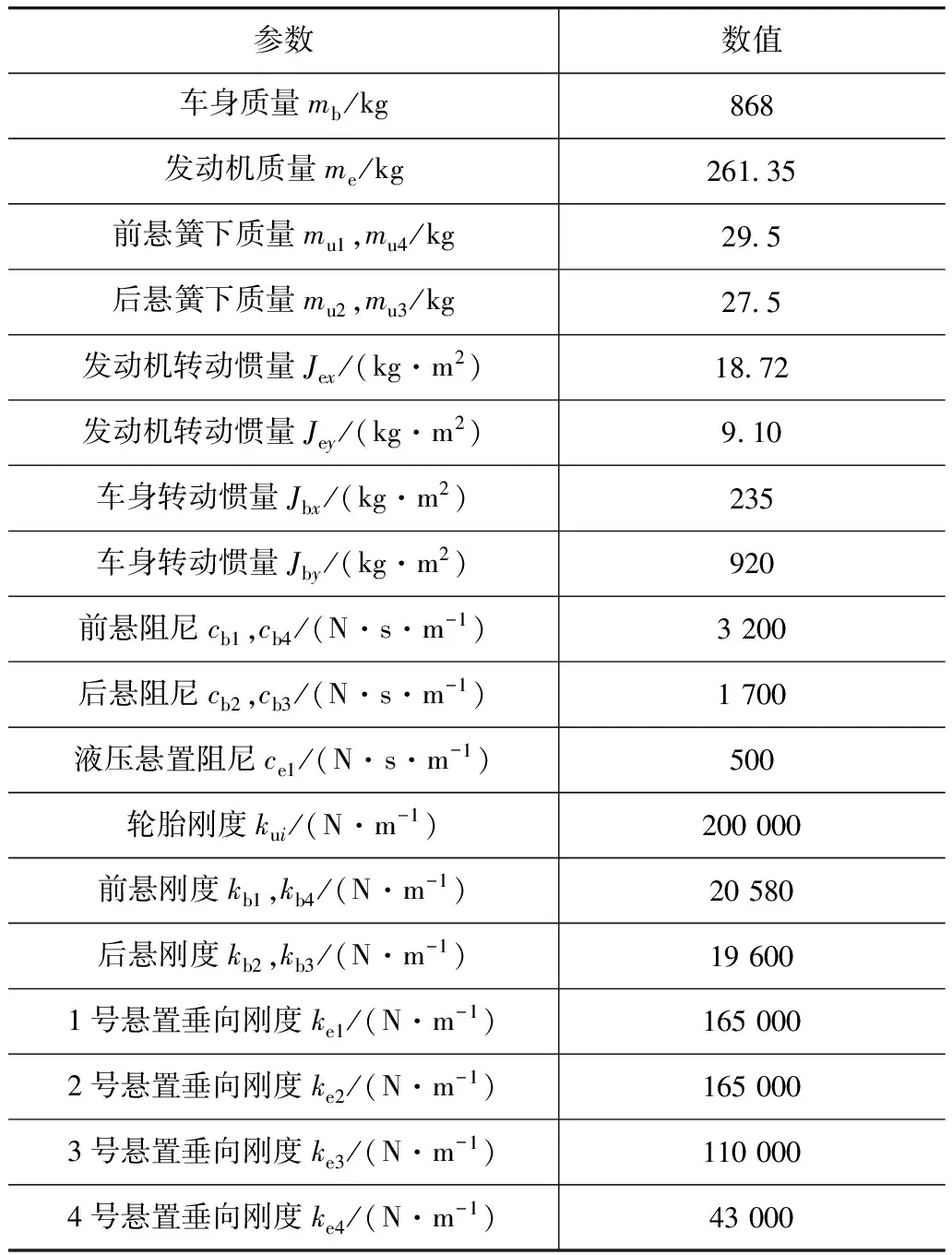
表2 整车参数

图10为两输入单输出变论域模糊控制器结构框图，输入论域由初始论域[-E,E]通过伸缩因子α变换为[-αE,αE]，输出论域由初始论域[-U,U]通过伸缩因子β变换为[-βU,βU]。α和β为误差变量的连续函数，本文中选择用函数模型来表述[17]，设定输入和输出论域伸缩因子为

(9)

式中：ei∈[-E,E]；ui∈[-U,U]；0<λi<1,i=1,2；0<γ<1。

发动机转速的变化范围为750～3 000r/min。变论域模糊控制器设计时，以悬置点垂向加速度e1=a和发动机2阶主频e2=f作为输入，输出量为磁流变悬置的可控阻尼力u，通过Elman网络磁流变悬置逆模型获得控制电流，再通过Elman网络磁流变悬置正模型获得实际控制的阻尼力。由于变论域模糊控制没有现成的Simulink框图，本文中通过编写S函数文件来实现。

输入量2阶主频变化范围为(0～100)Hz，加速度变化范围为(-20～20)m/s2，输出阻尼力变化范围为(-300～300)N。取输入量2阶主频模糊集合初始论域为(0～8)，对应模糊子集为{PZPSPMPBPL}，输入量加速度和输出量可控阻尼力模糊集合初始论域为[-6，6]，对应模糊子集为{NBNMNSNZPZPSPMPB}。以经验和理论推导，建立在“低频时使振动位移尽快衰减为零和高频时使振动速度尽快衰减为零”的控制原则。模糊控制规则如表3所示。

表3 模糊控制规则

4 仿真试验

利用Matlab/Simulink仿真软件，建立了基于被动液压悬置和磁流变液压悬置的发动机悬置系统仿真模型。仿真时，发动机采用单频率激励方式，路面等级为B级，以被动、模糊控制和变论域模糊控制策略作对比，对稳定转速为750r/min(汽车起动，不考虑路面输入，工况一)，稳定转速为1 000r/min(不考虑路面输入，工况二)，发动机转速为1 000r/min、车速20km/h(工况三)和发动机转速为2 000r/min、车速40km/h(工况四)时磁流变悬置点1的垂向振动加速度信号进行测量，结果分别如图11～图14所示，悬置点1的加速度均方根见表4。

从图11和图12可知：发动机转速分别为750和1 000r/min时，在激振频率即发动机振动2阶主频25和33.3Hz位置处，变论域模糊控制振动加速度功率谱幅值比被动悬置和模糊控制磁流变悬置均有明显下降；从表4可知，转速为750r/min时模糊控制和变论域模糊控制加速度均方根值分别比被动悬置降低了16.7%和38.0%；转速为1 000r/min时模糊控制和变论域模糊控制的加速度均方根值分别比被动悬置降低了13.8%和32.7%。

表4 悬置1点加速度的均方根值 m·s-2

从图13和图14可知：发动机转速为1 000r/min、车速20km/h和发动机转速为2 000r/min、车速40km/h时，在激振频率即发动机振动2阶主频33.3和66.7Hz位置处，变论域模糊控制振动加速度功率谱幅值比被动悬置和模糊控制磁流变悬置的振动加速度功率谱，均有明显下降；从表4可知，车速20km/h时，模糊控制和变论域模糊控制的加速度均方根值分别比被动悬置降低了12.6%和30%；车速40km/h时模糊控制和变论域模糊控制的加速度均方根值分别比被动悬置降低了10.5%和27.7%。

由于引入了路面输入，可以发现，相对于图11和图12，图13和图14中低频段10Hz以下的加速度频率响应曲线产生振荡，但模糊控制和变论域模糊控制仍具有较好的控制效果，且变论域模糊控制效果优于模糊控制。以上研究结果表明，变论域模糊控制器设计是合理和有效的，能很好地衰减发动机工作时的振动幅值。

5 结论

(1) 以磁流变悬置动态性能试验结果为数据样本，利用Elman神经网络的模型辨识方法，建立了磁流变悬置的正、逆模型。训练迭代进化曲线和辨识精度结果表明，Elman神经网络的训练速度快，具有高度的辨识性能，适用于多批次、数据量大的磁流变悬置力学模型辨识，具有较好的应用前景，为磁流变半主动悬置系统的工程应用奠定了基础。

(2) 综合考虑随机路面输入和发动机激励，建立了包含发动机悬置系统的整车10自由度力学模型，通过编写S函数文件，设计了变论域模糊控制策略；通过不同发动机转速和车速下悬置系统的仿真分析结果可知，在模糊控制规则相同的情况下，变论域模糊控制比传统模糊控制的控制精度更高。

[1] KOO J H, GONCALVES F D, AHMADIAN M. A Comprehensive Analysis of the Response Time of MR Dampers[J].Smart Materials and Structures,2006,15(2):351-358.

[2] HONGA S R, WERELEYA N M, CHOI Y T, et al. Analytical and Experimental Validation of a Nondimensional Bingham Model for Mixed-mode Magnetorheological Dampers[J]. Journal of Sound and Vibration,2008,312:399-417.

[3] SPENCER Jr B F,DYKE S J. Phenomenological Model of a Magnetorheological Dampers[J]. ASCE Joumal of Engineering Mechanics,1997,123(3):230-238.

[4] BOADA M J L, CALVO J A. Modeling of a Magnetorheological Damper by Recursive Lazy Learning[J]. International Journal of Non-Linear Mechanics 2011,46:479-485.

[5] SPENCER B, DYKE S, SAIN M, et al. Phenomenological Model for Magneto-rheological Dampers[J]. Journal of Engineering Mechanics,1997,123(3):230-238.

[6] GAMATO D, FILISKO F E. High Frequency Dynamic Mechanical Study of an Aluminosilicate Electrorheological Material[J]. Journal of Rheology,1991,35:1411-1425.

[7] 周强,瞿伟廉.磁流变阻尼器的两种力学模型和试验[J].地震工程与工程振动,2002,22(4):144-150.

[8] WERELEY N, PANG L. Nondimensional Analysis of Semi-active Electrorheological and Magneto-rheological Dampers Using Approximate Parallel Plate Models[J]. Smart Materials and Structures,1998,7:732-743.

[9] SPENCER JR B F, DYKE S J, SAINMK, et al. Phenomenological Model of a Magnetorheological Damper[J]. ASCE Joumal of Engineering Mechanics,1997,123(3):230-238.

[10] DU H, LAM J, ZHANG N. Modelling of a Magneto-rheological Damper by Evolving Radial Basis Function Networks[J]. Engineering Applications of Artificial Intelligence,2006,19(8):869-881.

[11] SCHURTER K, ROSCHKE P N. Fuzzy Modeling of a Magnetorheological Damper Using ANFIS[C]. The Ninth IEEE International Conference Fuzzy Systems,2000:122-127.

[12] WANG D H, LIAO W H. Neural Network Modeling and Controllers for Magnetorheological Fluid Dampers[C]. The 10th IEEE International Conference on Fuzzy Systems,2001:1323-1326.

[13] 李锐.发动机磁流变悬置隔振模糊控制与仿真[J].系统仿真学报,2009,21(4):944-947.

[14] CHOI S B, SONG H J, LEE H H. Vibration Control of a Passenger Vehicle Featuring Magnetorheological Engine Mounts[J]. International Journal of Vehicle Design,2003.33(1):2-16.

[15] YU Y H, NAGANATHAN N G, DUKKIPATI R V. A Literature Review of Automotive Vehicle Engine Mounting Systems[J]. Mechanism and Machine Theory,2001,36:123-142.

[16] 王昊,胡海岩.磁流变阻尼器的模糊逼近[J].振动工程学报,2006,19(1):31-36.

[17] 喻凡,郭孔辉.车辆悬架的最优自适应与自校正控制[J].汽车工程,1999,21(4):193-205.

Semi-active Vibration Control of a Vehicle FeaturingMagneto-rheological Engine Mount

Zheng Ling1,2, Deng Zhaoxue2, Pang Jian1,3, Xu Xiaomin1,3, Fu Jianghua1,3& Chen Daijun1,3

1.StateKeyLaboratoryofVehicleNVHandSafetyTechnology,Chongqing401120; 2.ChongqingUniversity,StateKeyLaboratoryofMechanicalTransmission,Chongqing400030; 3.ChanganAutoGlobalR&DCenter,Chongqing401120

For enhancing the modeling accuracy of the mechanical model for magneto-rheological (MR) engine mount and improving the vibration attenuation effects of engine mount system, An approach is proposed, in which the dynamic performance test results of MR mount are taken as data samples, the model identification is conducted on both forward and inverse models for MR mount with Elman neural network, and the model identified is used to control engine mount system. With concurrent consideration of random road input and engine excitation, a MR-based ten DOF vehicle dynamics model is built, a fuzzy controller with the variable universe of discourse is designed with engine speed and the acceleration signals at mounting points as inputs, and the semi-active control performance of MR mount is investigated. The simulation results show that compared with traditional fuzzy control, the fuzzy control with variable universe of discourse has better vibration isolation effects in wide frequency range and the peak vibration accelerations at mounting points significantly reduce. So the correctness and effectiveness of the model built and the corresponding fuzzy control algorithm with variable universe of discourse are verified.

engine; magneto-rheological mount; vibration control; Elman neural network; fuzzy control with variable universe of discourse

*汽车噪声振动和安全技术国家重点实验室开放基金课题(NVHSKL-201405)资助。

原稿收到日期为2014年8月25日，修改稿收到日期为2014年12月29日。