某多轴商用车平衡悬架高精度建模与分析*

段 亮，杨树凯，宋传学，范士琦，卢炳武

(1.吉林大学,汽车仿真与控制国家重点实验室，长春 130022； 2.汽车振动噪声与安全综合控制技术国家重点实验室，一汽技术中心，长春 130022)

2016037

某多轴商用车平衡悬架高精度建模与分析*

段 亮1，杨树凯2，宋传学1，范士琦1，卢炳武2

(1.吉林大学,汽车仿真与控制国家重点实验室，长春 130022； 2.汽车振动噪声与安全综合控制技术国家重点实验室，一汽技术中心，长春 130022)

鉴于Adams/Chassis的Leafspring专业模块本质上是针对传统钢板弹簧的建模，且对板簧端部接触和各片之间摩擦的定义比较粗糙，本文中在采用Leafspring专业模块自动生成钢板弹簧模型的基础上，对其某些部分进行了合理修正和重新定义，获得了平衡悬架钢板弹簧的修正模型,定义了其动刚度，并进行仿真，同时对其实物进行了力学特性试验。最后，分别以动刚度特性的“粘滞现象”和动刚度相对误差为指标，对修正模型和未修正模型的仿真结果与测试数据进行对比和评价。结果表明，本文中的修正模型在大大降低了复杂程度的前提下，达到了较高的分析精度(90%左右)，为整车动力学的分析提供了良好的平台。

多轴商用车；平衡悬架；钢板弹簧；端部接触；片间摩擦

前言

随着道路运输需求的增大和道路状况的改善，多轴商用车逐渐成为道路运输的主力，这就对商用车的平顺性和操纵稳定性提出了很高的要求。钢板弹簧是商用车悬架中应用最广的一种弹性元件，它几乎决定了车辆的平顺性和操纵稳定性，国内外学者对传统钢板弹簧进行了大量的深入研究[1-4]。但是对于多轴商用车而言，平衡悬架钢板弹簧与传统钢板弹簧的结构形式和安装方式均有很大不同，同时钢板弹簧本身存在非线性和迟滞特性，使平衡悬架钢板弹簧对于整车动力学的影响更加“扑朔迷离”，与此相关的研究也相当匮乏。

近些年来，针对钢板弹簧的研究主要集中在有限元建模方法和基于Adams/Chassis的Leafspring专业模块建模方法[5-8]。有限元建模方法能够精确地模拟板簧刚度、应力分布等动力学特性，包括对等刚度、复合刚度和渐变刚度的仿真计算，也能够模拟钢板弹簧的位移和变形等运动学特性，但是由于有限元模型所含自由度过多，难以应用到整车动力学仿真中，会造成模型计算困难，无法获得计算结果。因此，有限元建模方法主要用于钢板弹簧总成自身的仿真分析和验证各种简化板簧模型[9]。

为了满足厂家要求的平衡悬架钢板弹簧模型必须能够应用于整车动力学仿真分析，显然有限元建模方法很难满足这一要求。Leafspring专业模块本质上是针对传统钢板弹簧建模所设计的，平衡悬架钢板弹簧与传统钢板弹簧存在很大的不同，尤其是板簧各片之间接触位置的不确定导致了板簧刚度特性呈明显的非线性和迟滞特性，那么通过该专业模块自动生成的钢板弹簧模型显然无法很好地模拟平衡悬架钢板弹簧的相关特性。因此，本文中所建立的修正模型是基于Adams/Chassis的Leafspring专业模块二次开发。

1 高精度平衡悬架钢板弹簧模型的建立

1.1 Leafspring自动生成模型——未修正模型

利用Leafspring专业模块建立板簧模型时，只须输入平衡悬架钢板弹簧外形轮廓几何坐标、板簧结构几何参数、板簧的片数、离散梁单元的数目等，该专业模块将自动生成钢板弹簧模型，每一片板簧被离散成许多段刚性构件，这些离散后的刚性构件之间采用柔性梁进行连接，两个构件之间的作用力与反作用力通过Timoshenko梁理论进行计算，同时在板簧端部的各片之间创建接触力和摩擦力。关于Leafspring专业模块的使用方法见文献[12]。

钢板弹簧各片之间的摩擦力产生了非线性和迟滞特性，这种特性对钢板弹簧的刚度特性影响很大，本文中所研究的多轴商用车中后桥采用的平衡悬架是少片变截面钢板弹簧，该车辆在实际运行过程中，板簧各片之间的具体接触位置并不确定，但可以确定的是接触一定发生在板簧的端部，因此关于端部接触的定义和各片之间摩擦的计算是建立模型过程中非常关键的部分。虽然Leafspring专业模块自动生成的板簧模型在其端部使用了冲击函数Impact定义接触力，并且也定义了板簧各片之间的摩擦，但其定义很粗糙。第一，板簧端部的接触位置不断变化，而Leafspring自动生成的板簧模型却明确定义了端部接触的具体位置并且位置单一，显然无法准确描述端部接触这种不确定性。第二，各片之间的摩擦力也只是简单地利用阶跃函数来进行计算，并没有考虑到动、静摩擦之间的切换问题，显然与实际情况不符。通过上述分析，Leafspring自动生成的板簧模型明显无法满足要求，因此，需要在自动生成的板簧模型基础上，修正关于端部接触的定义和重新建立能够合理描述板簧各片之间摩擦的数学模型。

1.2 修正模型

首先，将描述板簧端部各片之间接触情况的接触力增加到4个，通过“以点代面”的思想尽可能扩展端部接触的范围以使端部接触逼近实际情况。新增加的端部接触仍然采用冲击函数Impact进行定义，图1所示为修正后模型某一处的端部接触示意图，冲击函数Impact的定义见文献[8]。

接下来，须要确定能够合理描述板簧各片之间摩擦特性的摩擦模型，关于摩擦模型的选择见文献[6]，最终本文中采用Coulomb摩擦来描述板簧各片之间的摩擦情况，如图2所示。其中，vs表示静滑移速度，vd表示动滑移速度，μs表示静摩擦因数，μd表示动摩擦因数。由于Coulomb摩擦是基于两个物体之间的相对运动速度来描述静摩擦和动摩擦特性，故当相对速度为正时，摩擦因数和摩擦力均为负值；反之亦然。由图2可知，当两个物体的相对速度绝对值在0和vs之间时，它们之间的摩擦处于静摩擦阶段；当两个物体的相对速度绝对值在vs和vd之间时，它们之间处于静摩擦向动摩擦转换的过渡阶段；当两个物体之间相对速度的绝对值大于vd时，它们之间处于动摩擦阶段。

须要强调的是，关于Coulomb摩擦模型中动、静摩擦因数和动、静滑移速度的确定绝对不能简单地借用其它类似文献中的数据，因为摩擦本身与相对速度、加速度、位移、润滑情况和接触表面的状况等因素有关；又考虑到平衡悬架钢板弹簧端部各片之间摩擦情况的特殊性，故本文中Coulomb摩擦模型的所有参数均需要在相关理论知识的基础上，结合试验测量，最后通过数据拟合来确定参数的具体值。在参数拟合过程中，板簧的动刚度特性对于板簧各片之间摩擦力的变化非常敏感，经过反复确定，结合试验数据，最终确定出平衡悬架钢板弹簧所采用的Coulomb摩擦数学模型的各项参数如表1所示。

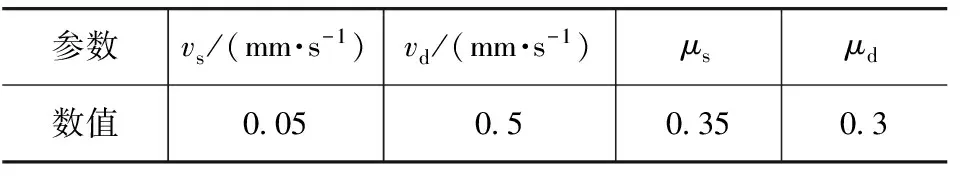
表1 Colulomb摩擦数学模型的各项参数

将自动生成的板簧模型进行上述修正后，接下来就须要定义平衡悬架钢板弹簧的支撑方式和施加外载荷从而验证板簧的力学特性。在实际车辆中，平衡悬架钢板弹簧两端自由支承在中、后桥半轴套管上的滑板式支架内，板簧两端自由灵活。文献[8]中指出采用运动副定义板簧底片处的支承，然而一旦定义运动副以后，相当于板簧底片只能沿着某一方向运动，不符合实际情况。为使所建立的板簧模型更接近实际，分别在板簧底片端部下方各建立一个圆柱体来模拟滑板式支架，然后分别使用固定副连接“支架”与大地。底片与“支架”之间的受力情况采用Adams/view中的特殊载荷contact来定义。当进行整车动力学仿真时，分别使用固定副连接“支架”与中、后桥，而不再是与大地相连。

须要解释的是，采用特殊载荷contact确实能够更准确地描述板簧端部接触，但却会大大增加模型的计算量，导致仿真计算困难。而实际上，在本文中定义的修正模型端部接触Three-Component Force中，各方向作用力的数学函数均与特殊载荷contact的计算方式一致，也即它近似等价于特殊载荷contact，这样在保证精度的前提下，大大降低了板簧模型的复杂程度和计算量。

2 模型仿真与试验验证

2.1 板簧试验

为验证平衡悬架虚拟样机模型的合理性和仿真结果的正确性，本文中对平衡悬架钢板弹簧进行了力学特性试验。钢板弹簧特性试验机如图3所示，采用液压加载方式，提供不同频率、不同幅值的正弦交变力，压头上装有高精度压力传感器，试验机由计算机控制，钢板弹簧试验的具体过程见文献[10]和文献[11]。

在本文中，分别进行了两组试验，第一组是静刚度试验，以频率f=30Hz、幅值F=180kN进行加载；第二组是动刚度试验，首先施以静载荷，待到静平衡之后再施以动载荷。该组试验共分为4次，分别以频率f为2，3和4Hz，幅值分别为30，11，8.5，3kN进行试验。试验结果见下文。

2.2 静刚度验证

静刚度指结构在静载荷作用下抵抗变形的能力。对于本文中的研究对象而言，虽然由于在静载荷的作用下，板簧各片之间仅处于接触状态而几乎没有产生相对运动，故静刚度几乎不受钢板弹簧非线性和迟滞特性的影响，但是为了说明平衡悬架钢板弹簧模型外部约束和支承方式的合理性，在这里仍然进行了静刚度的验证。图4所示为准静态加载工况(加载频率30Hz，载荷幅值180 kN)下未修正模型、修正模型和试验测量的静刚度对比曲线。

由图4可知，对于静刚度特性，无论是未修正模型还是修正模型均与试验测量相差非常小，在误差允许范围之内。

因此，可以得到如下结论：对于静刚度的模拟，未修正模型和修正模型都具有很高的精度。同时也说明，对于模型中板簧支承方式的定义和约束的施加等方面都是合理的，与试验基本一致。

2.3 动刚度验证

动刚度指结构在动载荷作用下抵抗变形的能力。由于车辆在实际行驶过程中，平衡悬架钢板弹簧承受来自不同路面施加的激励即动载荷作用，因此分析平衡悬架钢板弹簧的动刚度特性对于研究其对整车动力学的影响至关重要。不同加载工况下的未修正模型、修正模型的仿真结果与测试结果对比曲线分别如图5～图8所示。

由图5～图8可知，平衡悬架钢板弹簧在从加载向卸载过渡和从卸载向加载过渡时都出现了短暂的“粘滞现象”，换句话说，在过渡时由于板簧各片之间摩擦力方向的改变使各片之间“粘结”在一起变成刚体，从而在动刚度特性曲线的两端出现斜率有较大增加的现象[1-2]，这种现象对于分析钢板弹簧的力学特性非常关键，因此关于平衡悬架钢板弹簧模型的精度分析可分为“粘滞现象”的对比验证和计算动刚度数值的相对误差两部分。

3 模型的精度分析

为了从具体数值来说明本文中所建立的修正模型在分析平衡悬架钢板弹簧的动力学性能时所达到的精度，须要对模型精度进行分析。

3.1 动刚度的定义

前面已经提到，关于平衡悬架钢板弹簧模型的精度分析主要分为“粘滞现象”的对比验证以及计算动刚度数值的相对误差两部分。

首先，从不同加载工况下(图5～图8)的动刚度对比曲线能够明显看出，修正模型的“粘滞现象”非常接近试验结果，而未修正模型与试验偏差很大，说明修正模型与试验测量差别很小，具有较高精度。

接着，在试验测量的基础上，分别计算未修正模型和修正模型在不同加载工况下的动刚度。考虑到板簧力学特性的非线性，须对动刚度给出一个合理的定义。

图9所示为板簧力学特性的示意图。由图可知，动刚度曲线大致可以分为F-A-D段、D-E段、E-C-B段和B-F段。其中，F-A-D段和E-C-B段分别表示板簧正常加载和卸载阶段，D-E段和B-F段分别表示由加载向卸载过渡和由卸载向加载过渡的阶段。显然，D-E段和B-F段均出现了“粘滞现象”，其动刚度比F-A-D段和E-C-B段的刚度大得多。另外，F-A-D段和E-C-B段板簧力学特性呈近似线性变化，对应的动刚度基本相等，记为K1；同样，D-E段和B-F段也呈近似线性变化，对应的动刚度也基本不变，记为K2。

K1和K2的具体数值较难获得，因此，本文中定义了一个综合的钢板弹簧动刚度K：

(1)

式中：ΔF为载荷的变化量，Δx为板簧的变形量，它们分别对应图9中连线B-D的长度在纵轴和横轴的投影，而K则对应于该连线的斜率。

由于在实际试验中，动载荷是以正弦函数的形式施加，因此这里的ΔF为正弦函数幅值的2倍。Δx是动载荷在一个作用周期内板簧的总变形量。

3.2 相对误差的计算

根据式(1)动刚度的计算公式，分别计算出未修正模型和修正模型在承受不同载荷情况下的动刚度，然后结合试验测量数据得到各个模型的相对误差，最终计算结果如表2所示。

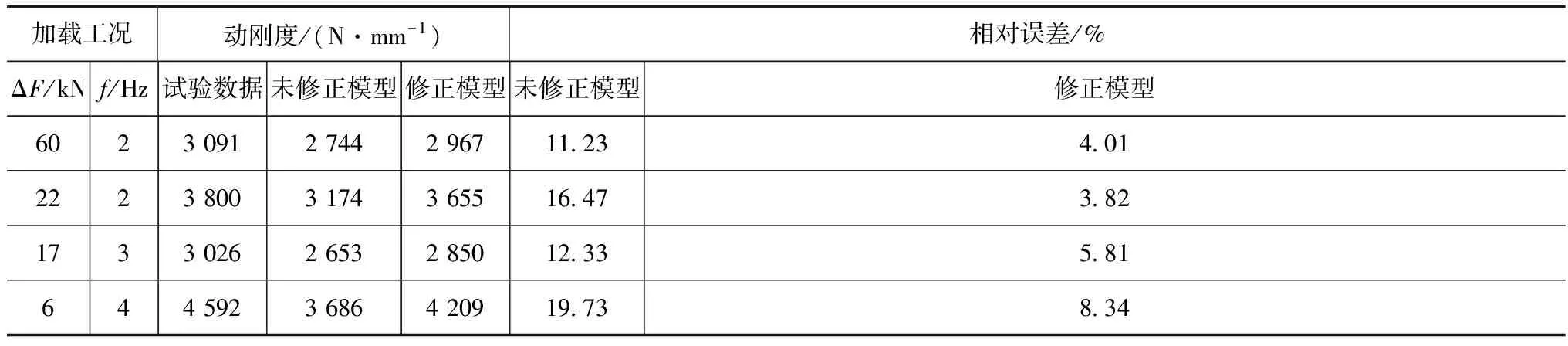
表2 未修正和修正模型相对误差计算结果

注：试验测量均在满载情况下测量，满载载荷为9t。f表示动载荷的频率，如ΔF=22kN，f=2Hz即表示动载荷的函数形式为F=11sin(4πt)+90。

由表2计算结果可得，当未修正和修正模型均在相同试验条件下进行仿真时，无论是哪种载荷形式，修正模型的相对误差基本上都可以控制在10%以内，即模型精度高达90%左右，这在工程应用中已足够。而对于未修正模型，其相对误差较大，很难模拟平衡悬架钢板弹簧的力学特性。

4 结论

从动刚度特性的“粘滞现象”对比和动刚度相对误差计算两个方面证实：由Adams/Chassis的Leafspring专业模块自动生成的未修正模型精度较低，难以用于平衡悬架钢板弹簧的深入研究，而本文中在深入分析平衡悬架钢板弹簧工作性质的基础上，所提出的修正模型却能够达到90%左右的高精度，同时也大大降低了模型的复杂程度，这种高精度的平衡悬架钢板弹簧多体动力学模型为整车动力学的分析提供了良好的平台，具有很好的现实意义。

[1]CEBOND.SimulationoftheResponseofLeafSpringstoBroadRandomExcitation[J].VehicleSystemsDynamics:InternationalJournalofVehicleMechanicsandMobility,1986,15:375-390.

[2]YOUNGYJ.FrictionalBehaviorofAutomotiveLeafSpring[C].ScienceandTechnology:KORUS2000.Proceedings,The4thKorea-RussiaInternationalSymposium,2000,3:5-10.

[3]ZAHAVIE.AnalysisofaContactProbleminLeafSprings[J].MechanicsResearchCommunications,1992,19(1):21-27.

[4]FANCHERPS,ERVINRD.MeasurementandRepresentationoftheMechanicalPropertiesofTruckLeafSprings[C].SAEPaper800905.

[5]CHENX,NAKAMURAK,MORIM.FiniteElementAnalysisforMulti-leafStructureswithFrictionalContactProblemswithFriction[J].ComputerAssistedMechanicsandEngineering,2000,7:53-67.

[6] 丁能根.钢板弹簧迟滞特性的有限元分析[J].汽车工程，2003, 25(1).

[7] 王其东.基于虚拟样机技术的汽车钢板弹簧设计与分析研究[J].机械工程学报，2001,37(12).

[8] 李杰.平衡悬架钢板弹簧模型的建立与仿真[J].重庆大学学报，2011,34(6).

[9] 吴碧磊.重型汽车动力学性能仿真研究与优化[D].长春：吉林大学，2008.

[10] 郑银环.汽车钢板弹簧计算模型研究[D].武汉：武汉理工大学，2005.

[11] 汤海洋.重型卡车后钢板弹簧刚度特性仿真分析及其对整车平顺性的影响研究[D].长沙：湖南大学，2010.

[12]MSCSoftware.UsingADAMS/CarLeafspring[R].Version2003.

High-accuracy Modeling and Analysis of Balanced Suspension in a Multi-axle Commercial Vehicle

Duan Liang1, Yang Shukai2, Song Chuanxue1, Fan Shiqi1& Lu Bingwu2

1.JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130022; 2.StateKeyLaboratoryofComprehensiveControlTechnologyonAutomobileVibrationNoiseandSafety,FAWRDC,Changchun130022

In view of that the professional module Leafspring in software Adams/Chassis is dedicated for the modeling of traditional leaf spring and is relatively coarse in defining leaf-end contact and interleaf friction, on the basis of automatically creating a leaf spring model with module Leafspring, its certain parts are reasonably modified and redefined to get a modified model for leaf springs of balanced suspension in this paper. Its dynamic stiffness is defined, a simulation is conducted and a corresponding test on its mechanical characteristics is performed. Finally with the "viscous hysteresis" of dynamic stiffness characteristics and the relative error of dynamic stiffness as indicators, the simulation results of modified model and original model and corresponding test data are compared and evaluated. The results show that with a greatly reduced complexity, the modified model achieves a high accuracy of about 90 percent, providing a good platform for further analysis of vehicle dynamics.

multi-axis commercial vehicle; balanced suspension; leaf spring; end contact; interleaf friction

*中国第一汽车集团公司技术中心项目(W65-GNZX-2014-0201)资助。

原稿收到日期为2014年9月5日，修改稿收到日期为2015年2月3日。