利用动量守恒定律计算炮车反冲速度时的一个常见错误
胡小龙
(铜陵市实验高级中学 安徽 铜陵 244000)
利用动量守恒定律计算炮车反冲速度时的一个常见错误
胡小龙
(铜陵市实验高级中学安徽 铜陵244000)
摘 要:反冲运动模型是动量守恒问题的一个经典模型[1],在讲解反冲模型时经常是以炮车斜向上发射炮弹为案例讲解,此时利用动量守恒定律计算炮车反冲速度时往往会混淆炮车炮筒的仰角和炮弹的发射角,以至于得不到准确的炮车反冲速度.
关键词:动量守恒反冲运动仰角发射角
【例题】如图1所示,质量为M的炮车静止放置在水平铁轨上,铁轨和炮车间摩擦不计,炮车炮筒与水平面夹角为θ,发射的炮弹质量为m,若发射的炮弹对地速度大小为v0,求炮车反冲速度v的大小?

图1
该问题一般给出的解答如下[2]:
如图2所示,由于铁轨和炮车间摩擦不计,因此炮车在发射炮弹时系统水平方向动量守恒,根据动量守恒定律有
mv0cosθ=Mv
解得
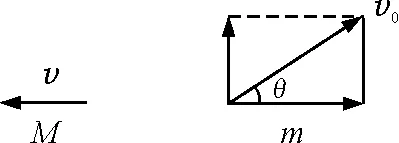
图2
以上解法究竟对不对呢?我们来分析一下:图2中的v0和v分别为炮弹和炮车相对于地面的速度,可以称之为发射速度和反冲速度.题中的角度θ是炮筒与水平面的夹角,称之为仰角,因为该角度并不等于炮弹射出炮筒时发射速度v0与水平面间的夹角,所以发射速度v0在水平方向的分速度并不等于v0cosθ,因此以上解法值得商榷.
图3给出了炮弹射出炮筒时的速度矢量关系图.其中v1为炮弹相对于炮车的速度,该速度与水平面间的夹角为θ;v为炮车对地的反冲速度;炮弹相对于地面的发射速度v0=v1+v.通过图3可知v0与水平面间的夹角并不是仰角θ,而是比θ大的角α,可称α为炮弹的发射角.
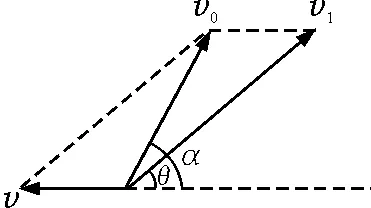
图3
在速度所构成的矢量三角形中利用余弦定理得到
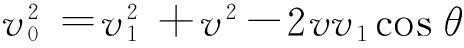
(1)
利用水平方向动量守恒得到
m(v1cosθ-v)=Mv
(2)
联立式(1)、(2)解得
(3)
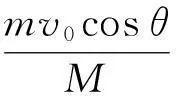
mv0cosα=Mv
(4)
式(3)代入式(4)得到
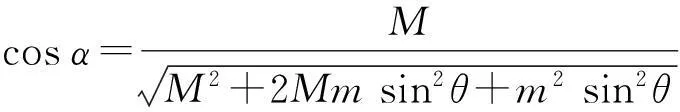
(5)

表1质量比值不同时炮车反冲速度v及发射角α大小
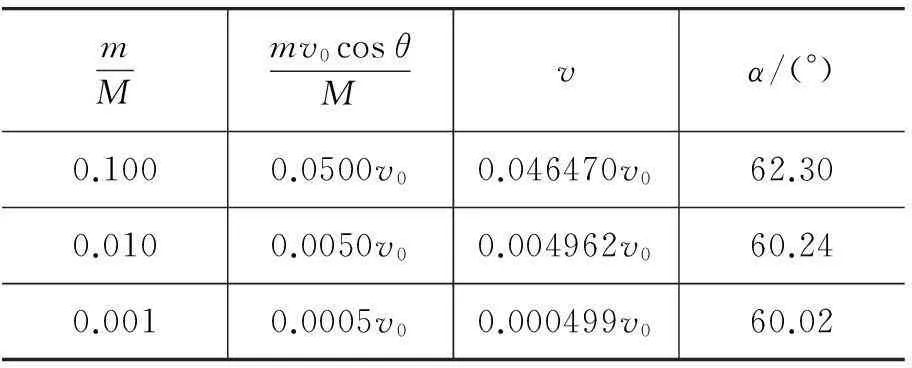
mMmv0cosθMvα/(°)0.1000.0500v00.046470v062.300.0100.0050v00.004962v060.240.0010.0005v00.000499v060.02
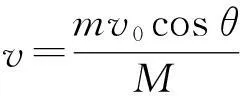
参 考 文 献
1杨宇红.如何理解和研究反冲运动.物理通报,2015(1):41
2罗小青. 浅谈在中专物理课程教学中动量守恒定律的应用.景德镇高专学报,2003(2):78
(收稿日期:2015-10-31)

