基于四元数自适应卡尔曼滤波的快速对准算法
徐晓苏,周 峰,张 涛,徐 祥
(1. 微惯性仪表与先进导航技术教育部重点实验室,南京 210096;2. 东南大学 仪器科学与工程学院,南京 210096)
基于四元数自适应卡尔曼滤波的快速对准算法
徐晓苏1,2,周 峰1,2,张 涛1,2,徐 祥1,2
(1. 微惯性仪表与先进导航技术教育部重点实验室,南京 210096;2. 东南大学 仪器科学与工程学院,南京 210096)
针对捷联惯导初始对准问题,提出了一种具有干扰抑制能力的四元数自适应卡尔曼滤波初始对准算法。通过将初始对准问题转化为Wahba姿态确定问题,直接建立四元数的滤波模型,并采用自适应卡尔曼滤波对初始时刻姿态四元数进行估计,利用姿态四元数更新求出当前姿态来实时地反映载体的姿态变化。针对直接构建量测模型导致收敛速度慢的问题,提出一种基于最优四元数估计法构造K矩阵原理的改进算法。利用三轴转台模拟不同的摇摆环境进行实验,转台实验表明了改进算法具有较快的收敛速度和良好的稳定性及精度,中等精度的惯导系统在150 s至200 s的对准时间内,航向角均值误差小于2′。
初始对准;四元数;自适应卡尔曼滤波;姿态确定
捷联惯性导航初始对准作为 SINS研究领域的关键技术之一,一直是国内外学者研究的热点。SINS初始对准一般分为粗对准阶段和精对准两个阶段:粗对准阶段大多数采用解析法完成,如凝固解析法;精对准阶段一般采用状态估计法,如卡尔曼滤波。SINS初始对准的本质是通过矢量观测来确定姿态,其求解的算法可分为确定性算法和状态估计法[1]。在确定性方法中,常用的有基于双矢量定姿原理的TRAID法[2-3]和基于求解特征值所对应的特征向量的最优四元数估计法[4-5]。传统TRAID法仅仅利用两个不同时刻的矢量观测信息,其余时刻的观测矢量信息并未充分利用,所选时刻观测矢量的精度对对准结果的影响较大。文献[6]中基于惯性空间中重力积分矢量的解析粗对准算法,研究了基于多矢量定姿的粗对准方法,虽然对观测矢量的利用率大大提升,但是对准精度同样与所选时刻观测矢量的精度有较大相关,并且不能实时地反应载体姿态的变化。文献[7-10]通过观测矢量和参考矢量构造出K矩阵,并采用相应的估计方法求出K矩阵特征值所对应的特征向量,其本质都为最优四元数估计法(q-method)。与双矢量定姿法相比,q-method具有较快的收敛速度和良好的精度。文献[1]中提出直接以对准初始时刻的四元数作为估计状态的四元数卡尔曼滤波初始对准算法,获得了较快的收敛速度和满意的精度,但在该文中所使用的卡尔曼滤波器算法中,需要提前获悉加速度计随机噪声的统计特性,才能保证滤波的稳定性。
本文同样直接以初始对准时刻的四元数作为估计状态,建立卡尔曼滤波模型,并采用实用的自适应卡尔曼滤波算法进行估计,该算法具有计算量小,滤波初始参数设置简单,易于工程实现的特点。针对本文提出的四元数自适应滤波算法存在收敛速度慢的问题,提出了一种改进的四元数自适应滤波算法。该算法基于最优四元数估计法构造K矩阵的原理,通过对观测模型中的观测矩阵进行改造,有效地加快了算法的收敛速度。三轴转台实验表明了本文提出的对准方法具有较快的收敛速度和良好的稳定性及精度。
1 坐标系定义
本文涉及的相关坐标系定义如下:
b—载体坐标系,原点位于载体的质心且与载体固连,x沿载体横轴向右,y沿载体纵轴向前,z沿载体立轴向上,xyz构成右手直角坐标系。
i—基座惯性坐标系,初始对准起始时刻,b系相对于惯性空间凝固后所得的惯性坐标系,它在惯性空间内的指向保持不变。
e—地心地球坐标系,原点位于地心且与地球固连,x轴在赤道平面内与本初子午线相交,y轴与z、x构成右手直角坐标系,z轴沿地球极轴的方向。
n—导航坐标系,x轴沿当地纬线切线指向东,y轴沿着当地经线方向指向北,z轴沿地理垂线向上,也被称为“东北天”坐标系。
2 四元数初始对准方法
2.1 最优四元数估计法
对准初始时刻t0,由于i系与载体系b系重合,所以根据四元数运算关系有:

在载体无线速度的情况下,由比力方程可得:
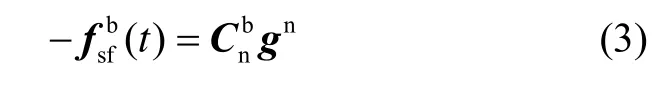
式(3)用四元数表示为:

将式(1)代入并整理可得:

令:
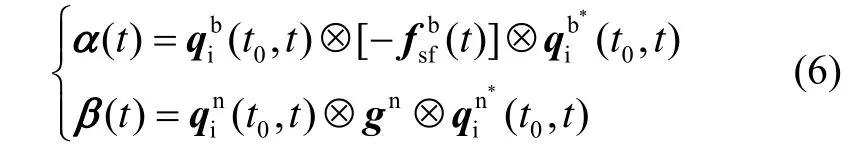
则式(5)可表示为:

令:

式中:(α×)、(β×)分别为以α、β向量构成的反对称矩阵。
式(7)可化为:

此时,根据最优姿态确定的方法,可将对准问题转化为Wahba姿态确定问题:
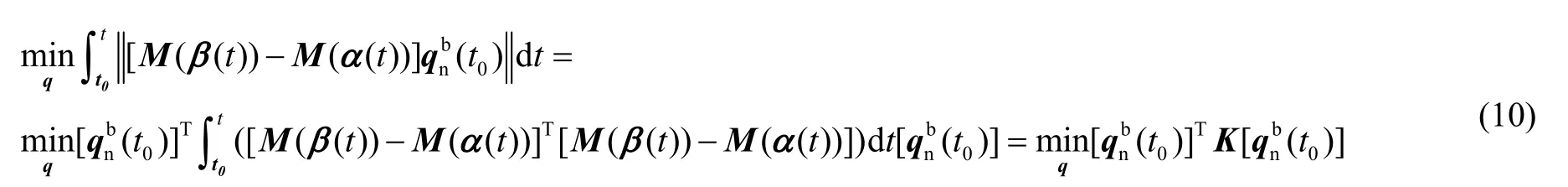

只要求出 K矩阵的最小特征值所对应的特征向量并归一化,即可求得再通过式(1)可求出
2.2 四元数自适应卡尔曼滤波法

式中,Qk和Qk-1分别表示在 tk和 tk-1时刻对应的
由式(9)可建立如下量测模型:

通过以上滤波模型的建立,利用实用的自适应卡尔曼滤波算法进行估计,具体估计过程如下:

2.3 摇摆基座仿真实验
摇摆基座仿真实验时采用的运动模型为:

式中:纵摇摇摆幅值Aθ=8°,摇摆频率fθ=0.15 Hz;横摇摇摆幅值Aγ=6°,摇摆频率fγ=0.2 Hz;航向摇摆幅值Aψ=5°,摇摆频率fψ=0.125 Hz;摇摆起始相位都为0°。仿真采用的捷联惯性仪表指标为:陀螺常值漂移0.01 (°)/h,陀螺随机漂移0.01 (°)/h;加速度计常值偏置 50 μg,加速度计随机偏置 50 μg;经度为118.786365°;纬度为 32.057313°;仪表采样频率为200 Hz;捷联解算周期为5 ms,仿真时间为200 s。
在水平姿态摇摆中心为 0°,航向角摇摆中心为45°时,两种对准方法的姿态误差结果如图1所示。

图1 最优四元数法和四元数滤波法对准姿态误差Fig.1 Alignment errors of q-method and QAKF
从图1中可以看出,相比于最优四元数法,四元数滤波法误差收敛速度很慢。为此,将针对四元数滤波法存在收敛速度慢的问题进行分析并对算法作改进。
3 问题分析及算法改进
3.1 四元数滤波法对准误差分析
根据式(6)得出,β(t)是通过当地重力加速度g从n系到i系转换得到的矢量,由于当地地理位置是已知的,因此,可以认为观测矢量β(t)是无误差的,即M(β(t))是无误差的。考察α(t),该观测矢量是加速度计输出构成的,而加速度计输出中包含加速度计零偏和随机偏置,因此,观测矢量α(t)中是包含误差的形式,即M(α(t))中是存在误差的,再由式(12)可知,四元数滤波法观测模型中的观测阵Hk是存在误差的。



式(16)两边同乘Qk并结合式(12)得:

将式(17)右边部分移至左边得:

从式(18)可以看出,实际的观测模型中包含了加速度计零偏和加速度计随机偏置相关项。由于在式(12)中直接忽略了加速度计零偏和随机偏置相关项的影响,所以从理论上分析得出,导致四元数滤波法收敛慢主要是由于加速度计零偏和随机偏置所致。
为了验证以上分析的正确性,本文设计加速度计随机偏置如表1所示的三种情况。

表1 三种加速度计随机偏置Tab.1 Three kinds of random bias of accelerometer
仿真实验其他条件不变,对准姿态误差如图2所示。
从图2中可以看出,在加速度计随机偏置为0 μg、50 μg和100 μg时,随着随机偏置的增大,航向角对准误差收敛速度由快到慢,且相差明显,因此,可以得出以下结论:四元数滤波法航向角的收敛速度对加速度计的随机偏置比较敏感,随机偏置越大,其收敛速度越慢。在实际工程当中,加速度计的随机偏置一般都较大,因此,若不对该算法进行改进,将不利于四元数滤波法的实际应用,甚至是失效。加速度计零偏对该算法的影响与随机偏置相似,由于篇幅所限,本文不再作分析。

图2 四元数滤波法三种随机偏置下的对准误差Fig.2 Alignment errors of QAKF with three kinds of random biases
3.2 改进四元数滤波法
本节通过最优四元数法构造K矩阵的原理,对四元数滤波法进行改进,以加快其收敛速度。构造如下K矩阵:
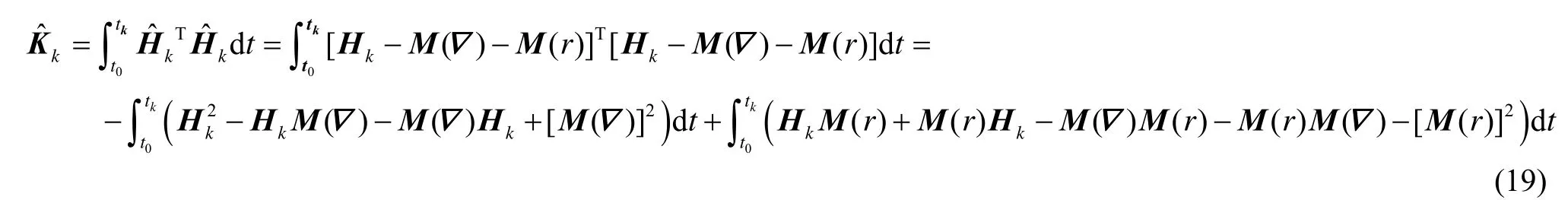
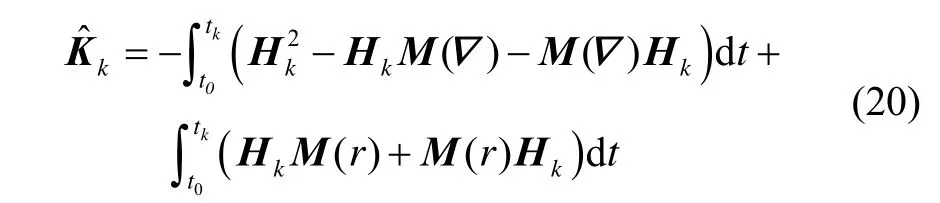
式(20)两边同乘Qk并结合式(12)得:

将式(21)右边部分移至左边得:

与式(18)相比较发现:加速度计零偏和随机偏置项以积分形式出现,且与矩阵相乘。由式不难得出各项元素都为小于 1的实数,因此,式(22)中加速度计零偏和随机偏置相关项的影响大为减小。
仿真实验条件同上,最优四元数法、四元数滤波法和改进四元数滤波法三者在20 s到200 s内的对准误差结果,如图3所示。
从图3中可以看出,改进的四元数滤波法的航向角误差收敛速度和精度都要明显优于四元数滤波法,且与最优四元数法相当。因此,本文提出的改进四元数滤波法有效。从图中亦可看出,改进四元数滤波法的稳定性要优于最优四元数法。为了更好地对比改进四元数滤波法和最优四元数法,将加速度计随机偏置设置为200 μg,其他仿真条件不变,对准姿态误差如图4所示。

图4 最优四元数法和改进四元数滤波法对准误差Fig.4 Alignment errors of q-method and improved-QAKF
通过图4可知,在加速度计具有较大的随机噪声下,改进四元数滤波法和最优四元数法的水平姿态精度相当且符合粗对准的极限精度,而两者的航向角对准误差在 150 s到 200 s以内的均值和标准差分别为0.0030°、0.0032°和 0.0050°、0.0056°。两者的航向角对准精度相当,但是,前者的稳定性要优于后者。从图中也可直观地看出,改进四元数滤波法的稳定性要优于最优四元数法。
4 转台实验验证及结果分析
为验证本文算法的有效性,利用FOSN光纤捷联惯组在三轴转台上完成不同实验条件下的对准实验,其中光纤陀螺的零位稳定性为0.006 (°)/h (1σ),零位重复性为0.006 (°)/h (1σ),随机游走系数为(1σ),石英挠性加速度计的零位稳定性为50 μg (1σ),零位重复性为50 μg (1σ),捷联惯组采样频率为200 Hz。捷联惯组安装如图5所示。

图5 捷联惯组在转台安装位置Fig.5 Placement of IMU on turntable
本文设计多组实验验证算法的有效性,实验1为静基座实验,实验2为小幅度摇摆实验,实验3为大幅度摇摆实验。为了更好地模拟舰船实际情况,纵摇、横摇和航向摇摆中心分别为2°、-2°和90°,纵摇角、横摇角和航向角的摇摆频率分别为0.15 Hz、0.2 Hz和0.125 Hz。实验条件设置如表2所示。

表2 实验条件设置Tab.2 Settings of experiment condition
鉴于篇幅所限,本文仅对实验3进行结果分析。实验3中,改进四元数滤波法的对准姿态变化如图6所示,改进四元数滤波法和最优四元数法在80 s 至200 s对准时间内的对准姿态误差如图7所示。
由图7可知,两者的水平姿态误差相当,但在航向角误差上,改进四元数滤波法的波动较小,稳定性明显优于最优四元数法。在80 s时,改进四元数滤波法的航向角误差为0.2366°。在对准150 s至200 s的时间内,改进四元数滤波法的均值和标准差分别为0.0198°和 0.0396°。改进四元数滤波法三组实验在对准150 s至200 s时间内的均值误差统计如表3所示。

图6 摇摆及对准姿态变化曲线Fig.6 Attitude changing curve of turntable and alignment

图7 改进四元数滤波法和最优四元数法对准误差Fig.7 Alignment errors of q-method and improved-QAKF

表3 对准实验结果Tab.3 Results of alignment experiment
5 结 论
本文针对捷联惯导初始对准问题,提出一种四元数自适应卡尔曼滤波对准算法。该算法直接对初始时刻姿态四元数进行估计,并采用了较为简单且易于工程实现的自适应卡尔曼滤波器。然而,仿真实验表明了该算法存在收敛速度慢的缺陷。通过对该问题的理论分析,本文进一步提出了一种改进的四元数自适应滤波算法。该算法基于最优四元数估计法构造K矩阵的原理,通过对观测模型中的观测矩阵进行改造,有效地降低了加速度计零偏和随机误差的影响。仿真实验及三轴转台实验表明了该算法的正确性和有效性。
(Reference):
[1] 周琪, 秦永元, 张金红, 等. 基于四元数卡尔曼滤波的捷联惯导初始对准算法[J]. 中国惯性技术学报, 2012, 20(2): 162-167. Zhou Qi, Qin Yong-yuan, Zhang Jin-hong, et al. Initial alignment algorithm for SINS based on quaternion Kalman filter[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 162-167.
[2] Cilden D, Conguroglu E S, Hajiyev C. Covariance analysis of three-axis attitude determination using two vector measurements[C]//International Conference on Recent Advances in Space Technologies. IEEE, 2015.
[3] Lee S H, Ahn H S, Yong K L. Three-axis attitude determination using incomplete vector observations[J]. Acta Astronautica, 2009, 65(7): 1089-1093.
[4] Shuster M D. Filter QUEST or REQUEST[J]. Journal of Guidance Control & Dynamics, 2012, 32(2): 643-645.
[5] Crassidis J L, Markley F L, Cheng Y. Survey of nonlinear attitude estimation methods[J]. Journal of Guidance Control & Dynamics, 2007, 30(1): 12-28.
[6] 郑振宇, 高延滨, 苑志江, 等. 捷联惯导系统惯性系粗对准原理及试验[J]. 中国航海, 2015, 38(04): 6-10. Zheng Zhen-yu, Gao Yan-bin, Yuan Zhi-jiang, et al. Principle and experimental study of coarse alignment of SINS in inertial frame[J]. Navigation of China, 2015, 38(4): 6-10.
[7] 李杨, 高敬东, 胡柏青, 等. 舰载捷联惯导动基座F-QUEST初始对准方法[J]. 海军工程大学学报, 2014(6): 32-36. Li Yang, Gao Jing-dong, Hu Bai-qing, et al. Shipborne SINS in-movement F-QUEST initial alignment algorithm [J]. Journal of Naval University of Engineering, 2014(6): 32-36.
[8] 高薪, 卞鸿巍, 傅中泽, 等. 捷联惯导晃动基座四元数估计对准算法[J]. 中国惯性技术学报, 2014, 22(6): 724-727, 740. Gao Xin, Bian Hong-wei, Fu Zhong-ze, Zhang Li-wei, et al. Alignment algorithm based on quaternion estimator for SINS on rocking base[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 724-727, 740.
[9] 王跃钢, 杨家胜, 杨波. 纬度未知条件下捷联惯导系统晃动基座的初始对准[J]. 航空学报, 2012, 33(12): 2322-2329. Wang Yue-gang, Yang Jia-sheng, Yang Bo. SINS initial alignment of swaying base under geographic latitude uncertainty[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2322-2329.
[10] Wu M, Wu Y, Hu X, et al. Optimization-based alignment for inertial navigation systems: Theory and algorithm[J]. Aerospace Science & Technology, 2011, 15(1): 1-17.
Initial alignment algorithm for SINS based on quaternion adaptive Kalman filter
XU Xiao-su1,2, ZHOU Feng1,2, ZHANG Tao1,2, XU Xiang1,2
(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University, Nanjing 210096, China; 2. School of Instrument Science & Engineering, Southeast University, Nanjing 210096, China)
An anti-disturbance initial alignment algorithm with quaternion adaptive Kalman filter is presented for strap-down inertial navigation system (SINS). By transforming the problem of initial alignment into Wahba attitude determination, the measurement model with quaternion is built directly, and an adaptive Kalman filter is adopted to estimate the initial attitude quaternion. By using the updating of attitude quaternion, the body’s current attitude is obtained to reflect the attitude’s change in real time. In view that the direct-constructed measurement model has the problem of slow convergence, an improved quaternion adaptive Kalman filter is proposed, which is based on the principle of building K matrix with optimal quaternion method, which has. Experiments under different swing environment with three-axis turntable show that this algorithm has fast convergence speed, high stability and good precision. The mean headingerror of the medium-accuracy SINS is less than 2′ for alignment time from 150 s to 200 s.
initial alignment; quaternion; adaptive Kalman filter; attitude determination
U666.1
:A
2016-05-21;
:2016-08-03
国家自然科学基金项目(51175082,61473085,51375088)
徐晓苏(1961—),男,博士生导师,从事测控技术与导航定位领域的研究。E-mail: xxs@seu.edu.cn
1005-6734(2016)04-0454-06
10.13695/j.cnki.12-1222/o3.2016.04.007

