采用超声电机的旋转式惯导系统转台
康国华,周琼峰,范 凯,马 云
(南京航空航天大学 航天学院,南京 210016)
采用超声电机的旋转式惯导系统转台
康国华,周琼峰,范 凯,马 云
(南京航空航天大学 航天学院,南京 210016)
目前国内外针对旋转式导航系统的研究表明,调制转台的性能直接影响到系统的导航精度。提出利用新型超声电机位移分辨率高、响应快、电磁兼容性好等特点,研制了高精度、低成本的超声电机调制转台,并实现了转台的非线性控制,从而增强导航系统旋转调制效果,进一步提高导航精度。相比于体积和功耗较大的常规电磁驱动旋转平台,该超声电机转台控制精度优于40″,响应时间优于5 ms,体积小,且无磁影响,有利于实现低成本、低精度的 MEMS旋转式导航系统的高精度应用,并进一步推动低成本微小卫星的应用和发展。
旋转式导航系统;旋转调制转台;MEMS;超声电机;非线性控制
随着惯性导航技术的发展,系统对惯性元器件的精度要求越来越高。在惯性元器件达到一定精度后,通过引入旋转调制技术来进一步提高惯性导航系统性能。
近年来,MEMS惯性技术日益成熟,在捷联惯性导航技术的基础上出现了一种新型的惯性导航系统,即基于MEMS技术的微型惯性导航系统[1-3]。MEMS惯性传感器体积小、抗冲击、可靠性高、寿命长、成本低,是一类非常适合于构建微型捷联惯性导航系统的惯性传感器。而根据MEMS器件零偏较大且零偏重复性较差的误差特性,旋转调制技术能发挥更明显的作用。
目前国内外旋转式捷联惯导系统多基于高精度的光纤陀螺和激光陀螺等,少有针对MEMS惯性元件的研究;且研制的单轴旋转调制系统如图 1所示[4],大多采用常规电磁驱动的旋转平台,其体积和功耗太大,不仅抵消了MEMS的优势,同时也带来比较严重的剩磁干扰。因此本文引入超声电机技术,研制高精度、低功耗、小体积的旋转调制转台,这对微型MEMS器件旋转调制导航系统的发展具有重要意义。

图1 单轴AN/WSN-7B系统结构Fig.1 Uniaxial AN/WSN-7B system structure
1 旋转调制原理
1.1 惯性器件误差补偿机制
旋转式捷联惯导系统误差调制技术是一种通过对惯性测量组合进行周期性的机械转动来实现对惯性器件误差补偿的技术。通过引入转动机构,在一个旋转周期内自动抵消惯性元器件常值漂移对导航所产生的误差,其实质是一种从系统角度消除误差的误差自补偿技术。
旋转调制转台与MEMS-IMU同轴安装,其示意图如图2所示,设MEMS-IMU仪东向、北向和天向漂移误差分别为εbx、εby、εbz,MEMS-IMU绕天向轴方向以角速率匀速旋转。

图2 旋转转台与MEMS-IMU的安装结构Fig.2 Installation structure of rotatory turntable and MEMS gyroscope
若载体坐标系与导航坐标系重合,得到t时刻后MEMS-IMU的漂移误差调制为
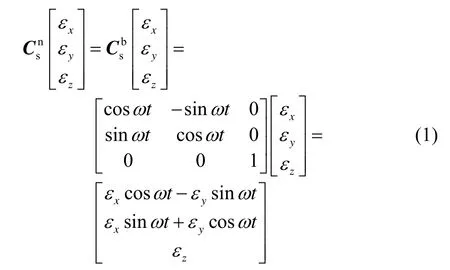
在一个转动周期τ,对上式进行积分运算得到

通过IMU绕天向轴的单轴旋转调制,可以消除MEMS惯性敏感轴与旋转轴垂直的漂移误差,从而减小这部分漂移误差对导航系统精度的影响;但沿着旋转轴方向上的陀螺仪和加速率计的常值漂移仍按着原来惯导系统原有的规律传播。
1.2 旋转调制转台误差分析
文献[8]提出旋转式捷联惯导系统转位机构自身的误差因素会对整个捷联算法回路产生影响,在导航解算的过程中,需要转位机构提供的数据有角位置信息和角速度信息。
1)若转位机构存在角位置误差δθ、角速度误差δω,则由转位机构误差引起的载体坐标系相对惯性坐标系在载体坐标系下的角速度误差为:

2)实际系统中,转位机构启动还有个加速过程,加速到恒定的调制角速度需要一定的加速时间,转位机构的加速和减速过程,直接影响了IMU的位置和速率的对称性。因此,转位机构启动和停止的过渡过程影响了误差调制的效果。设单轴连续旋转时间为t,若,则单轴连续旋转调制下,陀螺常值漂移引起的系统姿态误差为:
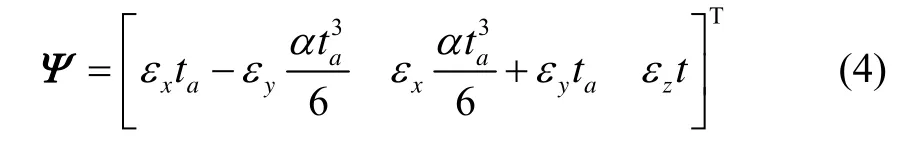
式中:εx、εy、εz为陀螺的常值漂移,α表示转位机构的角加速度,ta表示加速时间。从式(4)可以看出,其加速阶段会引起水平姿态误差的常值分量,该误差在以后的匀速转动阶段会一直保持下去。
3)对于MEMS陀螺,其零偏较大,且易受磁场环境影响。
本文针对MEMS陀螺(ADIS16405)在不同磁场环境中的常值漂移进行了测试,如图3~5所示。
图 3为测试系统环境,主要包括地磁模拟器、MEMS陀螺以及上位机软件。图4为不同磁场环境下三轴角速率平均值。图5为不同磁场环境下三轴角速率标准差。从图4可以看出,磁场环境对三轴角速率的平均值有很大的影响,磁场强度的绝对值越大,陀螺的角速率输出越小,且磁场接近于地表值的时候陀螺角速率值最大,越接近真值。从图5可以看出,标准差与磁场强度成二次曲线关系,磁场强度的绝对值越大,角速率的标准差越大,即磁场强度会增加陀螺的常值漂移。所以在研究基于MEMS旋转调制导航系统时,若有较大的外加磁场干扰,如达到 105nT,对零漂就有一定的影响。对于传统的电磁电机会有较大的剩磁干扰,如力矩电机的漏磁场,则需要克服外加磁场对MEMS陀螺的影响。
综上旋转调制误差分析可以看出,研制高精度、响应时间短、电磁兼容性好的旋转调制转台是提高基于MEMS旋转调制导航系统精度的关键。

图3 测试系统环境Fig.3 Environment of the test system

图4 不同磁场环境下三轴角速率平均值Fig.4 Average three-axis angular rate under different magnetic field environments

图5 不同磁场环境下三轴角速率标准差Fig.5 Three-axis angular rate standard deviation under different magnetic field environments
2 微型超声电机转台
2.1 转台特性
超声电机是一种全新理念的电动机,它是利用压电陶瓷元件激发定子的振动、转子之间的摩擦作用而工作的,由于它的特殊工作原理,使其与传统电磁电机相比具有比较显著的特点:1)断电自锁;2)低速大扭矩。3)结构简单、转矩/重量比大、体积小;4)转动部件的惯性小,响应快,定位精度高,起动和停止时间为ms量级;5)外形结构设计趋于多样化,适应不同的使用场合;6)电磁兼容性好,既不产生磁场,也不受磁场影响;7)不易受真空环境影响。
上述特点使得用超声电机转台相比普通电机驱动的转台具有独特优势。
本课题组研制的超声电机转台如图6所示。
该超声电机转台性能指标如下:
1)往复旋转功能:能够在0°~ 360°之间以指令角速率恒速往复运动,速度、停转时间可控,角速率范围不小于±100 (°)/s;

图6 超声电机转台的实物图Fig.6 Physical picture of ultrasonic motor turntable
2)角位置测量精度:优于40″(3σ);
3)锁定功能:锁定精度优于2.5′(3σ),锁定后精度优于40″(3σ);
4)旋转角速率换向时间:小于 5 ms,由静止达到某一速率的启动时间和对应的停止时间小于2 s;
5)有效载荷:0.3~0.6 kg;
6)转台尺寸:100 mm×100 mm×37 mm。
2.2 转台非线性控制
虽然超声电机转台具有许多传统电磁驱动转台所没有的优点,但其转速具有很强时变性和非线性,即其输出特性会随着环境温度、摩擦损耗、预压力、驱动器激励频率等因素的变化而变化,所以建立适用于超声电机控制的非线性数学模型是一项技术难点。
超声电机转台的控制方式根据控制量不同主要有三种,如表1所示。表1结果表明,频率调节比较适合与速度控制,而相位调节比较适合于位置控制。本文以电压频率作为控制量,采用增量式PID算法实现超声电机转台的非线性控制。
该算法具有以下优点:计算机只输出控制增量,误动作影响较小,切换时冲击小,算式无需累加,只需记住四个历史数据,占用内存小,算法简单,计算方便。其数学模型如下:

式中:k为采样序号,uk-1为第k-1次采样时刻的计算机输出值,ek-1为第k-1次采样时刻输入的偏差值,ek-2为第k-2次采样时刻输入的偏差值,KP为比例系数。增量式PID控制器系统如图7所示,比较简单,易于实现。
超声电机转台控制程序流程如图8所示,采用定时中断方式,采样周期为10 ms,提高控制实时性。

图7 增量式PID控制器系统Fig.7 Incremental PID controller system

图8 超声电机控制程序流程图Fig.8 Flow chart of ultrasonic motor control program

表1 超声电机的控制方式对比Tab.1 Comparison on ultrasonic motor control modes
3 转台性能测试
本课题组按响应时间、角速率精度、角位置精度这3个主要技术指标对转台进行测试。
3.1 响应时间
图9为超声电机转台从启动到转速为10 (°)/s再到关断的速度响应曲线,每1 ms读取一次数据。从测试曲线可以看出,启动和关断响应时间都在毫秒级,几乎可忽略不计。所以针对超声电机旋转调制转台模型可以忽略电机角加速度,即前文提到的转位机构加速时间对调制效果影响可以不考虑,从而降低由转台导致的导航误差。

图9 超声电机启动和关断响应曲线Fig.9 Start and shut-off response curves of ultrasonic motor
3.2 角速率精度
通过输入不同的角速率指令,每10 ms采集一次转台的角速率输出,对超声电机转台角速率精度进行了测试,结果如图10所示。
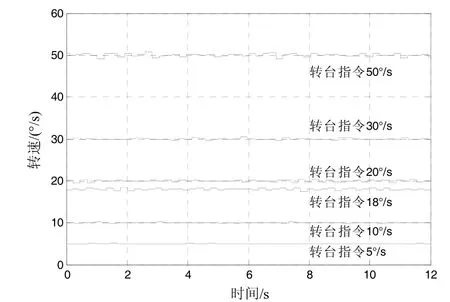
图10 超声电机转台速度曲线Fig.10 Turntable speed curves of ultrasonic motor
表2为超声电机转台角速率对应的平均转速误差。从结果分析来看,超声电机转台的角速率精度很高,达到10-5这个数量级,但随着旋转角速率的增加,平均误差会有相应的增加,所以为更好地提高导航精度,转台需要选取合适的调制角速率范围。

表2 转台角速率对应的平均转速误差Tab. 2 Average speed errors corresponding to turntable rates
3.3 角位置精度
1)选取了四个角位置进行测试,以编码器的 0°位置作为转台的0°位置,输入转台角位置控制指令,达到指定角位置后输出当前角位置,得到的结果如表3所示。从表3可以看出,超声电机的角位置误差在0.01°量级,即优于 40″,说明转台的定位精度达到了技术指标。
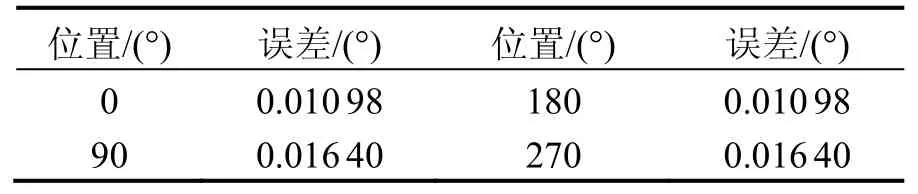
表3 角位置与角位置误差Tab.3 Angular position and angular position error
2)对转台进行不同角速率下的往复运动测试,结果如图11所示。


图11 不同角速率往复运动的角位置曲线Fig.11 The reciprocating motion curves of angular position towards different angular rates
从测试结果可以看出,超声电机转台的角位置
控制精度很高,且往复旋转重复性很好,换向时间优于5 ms,满足指标。对于正反旋转调制的方案来说,超声电机转台相比于比普通的电磁电机转台,更有利于提高旋转调制的效果。
4 总 结
上述研究结果表明,对于 MEMS旋转调制导航系统,本课题组研制的超声电机转台具有以下优势:1)转位机构的精度高,误差小,响应快;2)体积小,成本低,电磁兼容性好,能够充分发挥MEMS陀螺的优势。本文通过采用增量式PID算法解决了超声电机转台的非线性控制问题,其控制精度、响应时间等性能都达到了预设技术指标。通过磁环境测试、转台性能测试等证明了超声电机转台有利于提高旋转调制导航系统的精度。通过超声电机转台的设计与实现验证了超声电机转台的可实现性和应用性,有利于实现低成本、低精度MEMS导航系统的高精度应用,推动旋转式导航系统的发展。
(References):
[1] 孙伟, 初婧, 丁伟, 等. 基于IMU旋转的MEMS器件误差调制技术研究[J]. 电子测量与仪器学报, 2015(2): 240-246. Sun Wei, Chu Jing, Ding Wei, et al. Research on rotary MEMS device error modulation technology based on IMU[J]. Journal of Electronic Measurement and Instrument, 2015(2): 240-246.
[2] 徐烨烽, 仇海涛, 何孟珂, 等. MEMS旋转调制式航姿参考系统设计及误差补偿[J]. 兵工学报, 2011, 32(6): 691-696. Xu Ye-feng, Chou Hai-tao, He Meng-ke, et al. MEMS rotation modulation navigation position reference system design and error compensation[J]. Acta Armamentarii Journal of China Ordnance, 2011, 32(6): 691-696.
[3] 王学运, 吕妍红, 王玮, 等. MEMS器件捷联惯导系统旋转调制技术[J]. 东北大学学报(自然科学版), 2014, 35(4): 494-498. Wang Xue-yun, Lv Yan-hong, Wang Wei, et al. Rotating modulation technology of strapdown inertial navigation system on MEMS devices[J]. Journal of Northeastern University(Natural Science Edition), 2014, 35(4): 494-498.
[4] Chen Xi-Yuan, Yu Jing, Zhu Xue-Fen. Theoretical analysis and application of Kalman filters for ultra-tight global position system/inertial navigation system integration[J]. Transactions of the Institute of Measurement and Control, 2012(5): 648-662.
[5] Zhang Lun-dong, Lian Jun-xiang, Wu Mei-ping, et al. An improved computation scheme of strapdown inertial navigation system using rotation technique[J]. Journal of Central South University of Technology, 2012(5): 1258-1266.
[6] Zhi Shen, Georgy J, Korenberg M J, et al. Low cost two dimension navigation using an augmented Kalman filter/Fast Orthogonal Search module for the integration of reduced inertial sensor system and Global Positioning System[J]. Transportation Research Part C, 2011(6): 1111-1132.
[7] Wu Dan-yu, Chen Jian-wu, Chen Gao-peng, et al. An ultra-high-speed direct digital synthesizer with nonlinear DAC and wave correction ROM[J]. Analog Integrated Circuits and Signal Processing, 2012(1): 291-300.
[8] 牛小骥, 王强, 李由, 等. 利用伪观测取代精密转台的原地旋转调制寻北[J]. 中国惯性技术学报, 2015, 23(6): 707-713. Niu Xiao-ji, Wang Qiang, Li You, et al. Research on the key technology of rotary strapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 707-713.
[9] 陈曦. 基于MEMS惯性传感器的高精度姿态测量关键技术研究[D]. 浙江大学, 2014. Chen Xi. Key technology research on attitude measurement based on MEMS sensors[D]. Zhejiang University, 2014.
[10] Nguyen H T, Odomari S, Yoshida T, et al. Digital position control strategy of traveling-wave ultrasonic motors[J]. AUTOMATIKA: Journal for Control, Measurement, Electronics, Computing and Communications, 2014(3): 246-255.
[11] Velázquez R, Hernández H, Gutiérrez C A, et al. An analytical and experimental study of ultrasonic linear motors[J]. Technical Gazette, 2015(4): 1057-1063.
[12] Pei Fu-jun, Zhu Li, Zhao Jian, et al. Initial self-alignment for marine rotary SINS using novel adaptive Kalman filter [J]. Mathematical Problems in Engineering, 2015, 29: 1-12.
[13] Yuan Zhen-guo, Zhao Lin. Error analysis of rotray SINS sensor[J]. Sensors & Transducers, 2013, 156(9): 35-39.
Rotary inertial navigation system turntable based on ultrasonic motor
KANG Guo-hua, ZHOU Qiong-feng, FAN Kai, MA-Yun
( Institute of Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
As the domestic and oversea research on rotary navigation system illustrated, the performances of the modulated turntable can directly influence the system’s navigation precision. To solve this problem, a high-precision and low-cost ultrasonic motor modulated turntable is developed and the nonlinear control of the turntable was realized, based on the characteristics of a new ultrasonic motor, such as high displacement resolution, fast response, and good electromagnetic compatibility, etc. Thus, the rotating modulation effect is enhanced, and the navigation accuracy is further improved. Compared to the larger volume and power consumption of conventional electromagnetic driving rotating platform, the control precision of the ultrasonic motor turntable is better than 40″, the response time is less than 5 ms, the volume is smaller, and there is no magnetic influence, which is conducive to realizing high-precision application with low-cost and low-precision MEMS rotary navigation system, and further promoting the application and development of low-cost micro-satellite.
rotary navigation system; rotary modulation turntable; MEMS; ultrasonic motor; nonlinear control
V448.2
:A
2016-04-01;
:2016-07-08
江苏省自然科学基金(SBK201343261);中央高校基本科研业务费专项资金资助(NS2014092)
康国华(1978—),男,教授,硕士生导师。E-mail: kanggh@nuaa.edu.cn

